Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(i) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(i)
Question 1.
Δ ABC ଅଙ୍କନ କର ଯାହାର BC = 5.8 ସେ.ମି., m∠B = 60° ଓ A͞D ଲମ୍ବର ଦୈର୍ଘ୍ୟ = 4.2 ସେ.ମି. । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
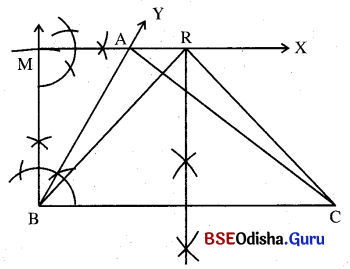
(a) 5.8 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ B͞C ଅଙ୍କନ କର ।
(b) B ବିନ୍ଦୁରେ \(\overrightarrow{\mathrm{BM}}\) ଲମ୍ବ ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 4.2 ସେ.ମି. ଏବଂ B ବିନ୍ଦୁରେ ∠YBC ଅଙ୍କନ କର ଯାହାର ପରିମାଣ 60° ହେବ ।
(c) M ବିନ୍ଦୁରେ B͞C ସହ ସମାନ୍ତର କରି \(\overrightarrow{\mathrm{MX}}\) ଅଙ୍କନ କର ଯାହା \(\overrightarrow{\mathrm{BY}}\) କୁ A ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
(d) A͞C ଅଙ୍କନ କରି Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(e) BC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ \(\overrightarrow{\mathrm{MX}}\) କୁ R ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(f) R͞B ଓ R͞C ଅଙ୍କନ କରି Δ ABC ର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ Δ RBC ପାଇପାରିବ ।
![]()
Question 2.
Δ ABC ଅଙ୍କନ କର ଯାହାର BC = 5.4 ସେ.ମି., m∠B = 60°, m∠A = 75° । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କର । ଭୂମି B͞D ର ଦୈର୍ଘ୍ୟ 6.3 ସେ.ମି. ନେଇ (ଯେପରି B – C – D) BD ଉପରେ Δ ABC ର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ Δ A’BD ଅଙ୍କନ କର ।
ସମାଧାନ:
ତ୍ରିଭୁଜର ତିନି କୋଣର ସମଷ୍ଟି 180° ।
ଅଙ୍କନ ପ୍ରଣାଳୀ :
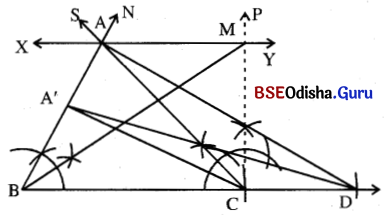
m∠A = 75°, m∠60°
⇒ m∠C = 45°
(a) B͞C ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 5.4 ସେ.ମି. ।
(b) BC ର B ବିନ୍ଦୁରେ ∠NBC ଏବଂ C ବିନ୍ଦୁରେ ∠SCB ଅଙ୍କନ କର ଯେପରିକି ସେମାନଙ୍କର ପରିମାଣ ଯଥାକ୍ରମେ 60° ଏବଂ 45° ହେବ ।
(c) A ବିନ୍ଦୁରେ BC ସହ ସମାନ୍ତର କରି \(\overrightarrow{\mathrm{XY}}\) ଅଙ୍କନ କର ।
(d) C ବିନ୍ଦୁରେ BC ପ୍ରତି CP ଲମ୍ବ ଅଙ୍କନ କର, ଏହା \(\overrightarrow{\mathrm{XY}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(e) M͞B ଅଙ୍କନ କରି Δ MBC ସଂପୂର୍ଣ୍ଣ କର ।
(f) ପୁନଶ୍ଚ \(\overrightarrow{\mathrm{BC}}\) ଉପରେ D ଏପରି ଏକ ବିନ୍ଦୁ ଯପରିକି B – C – D ଏବଂ BD = 6.3 ସେ.ମି. ହେବ ।
(g) A͞D ଅଙ୍କନ କର ଏବଂ AD ସହ ସମାନ୍ତର କରି C ବିନ୍ଦୁରେ A’C ଅଙ୍କନ କର ।
(h) A͞’D ଅଙ୍କନ କରି ଆବଶ୍ୟକୀୟ Δ A’BD ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 3.
Δ ABC ଅଙ୍କନ କର ଯାହାର A ରୁ B͞C ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 6.7 ସେ.ମି., m∠B = 60° ଓ m∠C = 45° । ଏହାର ଅର୍ଦ୍ଧେକ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
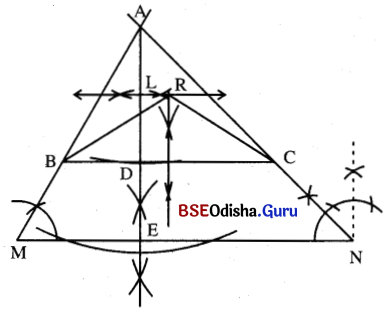
(a) Δ AMN ଅଙ୍କନ କର ଯାହାର m∠M = 60°, m∠N = 45° ଏବଂ M͞N ର ଦୈର୍ଘ୍ୟ ଯେକୌଣସି ବାସ୍ତବ ସଂଖ୍ୟା ହୋଇପାରେ ।
(b) A͞E ⊥ M͞N ଅଙ୍କନ କର ।
(c) A͞E ଉପରିସ୍ଥ D ଏକ ବିନ୍ଦୁ ହେଉ ଯେପରିକି AD = 6.7 ସେ.ମି. ଏବଂ A – D – E ଅଥବା A – E – D ହେବ ।
(d) M͞N ସହ ସମାନ୍ତର କରି B͞C ଅଙ୍କନ କର ।
(e) A͞D ର ମଧ୍ୟବିନ୍ଦୁ L ନିର୍ଣ୍ଣୟ କର ଏବଂ L ଠାରେ B͞C ସହ ସମାନ୍ତ ର କରି \(\overleftrightarrow{\mathrm{LR}}\) ଅଙ୍କନ କର ।
(f) B͞C ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ \(\overleftrightarrow{\mathrm{LR}}\) କୁ R ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(g) R͞B ଓ R͞C ଅଙ୍କନ କରି Δ RBC ଆବଶ୍ୟକୀୟ ତ୍ରିଭୁଜ ସମ୍ପୂର୍ଣ୍ଣ କର ।
ବିକଳ୍ପ ପ୍ରଣାଳୀ :
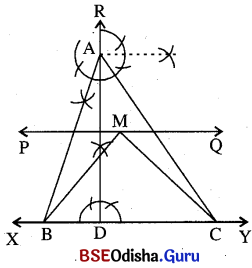
(a) ଯେକୌଣସି ଏକ ରେଖା XY ଅଙ୍କନ କର । \(\overleftrightarrow{\mathrm{XY}}\) ର ଯେକୌଣସି ଏକ ବିନ୍ଦୁ D ରେ DM ⊥ \(\overleftrightarrow{\mathrm{XY}}\) ଅଙ୍କନ କର ।
(b) A ବିନ୍ଦୁରେ AD ଉପରେ ଯଥାକ୍ରମେ m∠BAD = 30° ଓ 45° ଅଙ୍କନ କରି Δ ABC ସଂପୂର୍ଣ୍ଣ କର ।
(c) AD ର ସମଦ୍ବିଖଣ୍ଡକ ରେଖା \(\overleftrightarrow{\mathrm{PQ}}\) ଏବଂ BC ର ସମଦ୍ବିଖଣ୍ଡକ ରେଖା KM ଅଙ୍କନ କର ।
(d) MB ଓ MC ଅଙ୍କନ କରି Δ ABC ସଂପୂର୍ଣ୍ଣ କର ।
(e) Δ MBD, Δ ABC ର ଅର୍ଦ୍ଧେକ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ହେବ ।
![]()
Question 4.
Δ ABC ରେ m∠B = 60°, AX ଲମ୍ବର ଦୈର୍ଘ୍ୟ 4.9 ସେ.ମି. ଓ m∠A = 45°, ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରି ତା’ର ଦୁଇଗୁଣ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
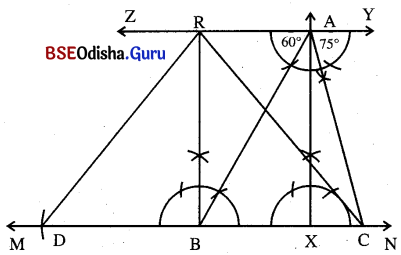
(a) \(\overleftrightarrow{\mathrm{MN}}\) ଉପରିସ୍ଥ X ବିନ୍ଦୁରେ A͞X ଲମ୍ବ ଅଙ୍କନ କର ।
(b) A ବିନ୍ଦୁରେ \(\overleftrightarrow{\mathrm{MN}}\) ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{ZY}}\) ଅଙ୍କନ କର ।
(c) A ବିନ୍ଦୁରେ ∠YAC ଓ ∠ZAB ଅଙ୍କନ କର ଯେପରିକି ସେମାନଙ୍କର ପରିମାଣ ଯଥାକ୍ରମେ 75° ଓ 60° ହେବ । Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(d) \(\overrightarrow{\mathrm{CB}}\) ଉପରିସ୍ଥ D ଏକ ବିନ୍ଦୁ ଯେପରିକି C – B – D ଏବଂ BC = BD ହେବ ।
(e) B ବିନ୍ଦୁରେ ଅଙ୍କିତ ଲମ୍ବ \(\overleftrightarrow{\mathrm{ZY}}\) କୁ R ବିନ୍ଦୁରେ ଛେଦ କରୁ । R͞D ଓ R͞C ଅଙ୍କନ କର ।
(f) Δ RDC ଆବଶ୍ୟକୀୟ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ, ଯାହାର କ୍ଷେତ୍ରଫଳ Δ ABC ର କ୍ଷେତ୍ରଫଳର ଦୁଇଗୁଣ ।
Question 5.
Δ ABC ରେ BC = 6.5 ସେ.ମି., b + c = 10 ସେ.ମି. ଓ m∠B = 60° । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରି ଏହାର ଦୁଇଗୁଣ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
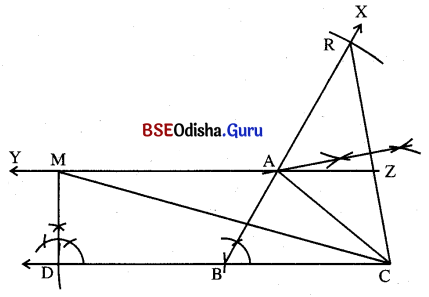
(a) 6.5 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ BC ଅଙ୍କନ କର ।
(b) BC ର B ବିନ୍ଦୁରେ 60° ପରିମାଣ ବିଶିଷ୍ଟ ∠CBX ଅଙ୍କନ କର ।
(c) \(\overrightarrow{\mathrm{BX}}\) ଉପରେ R ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି BR = 10 ସେ.ମି. ହେବ । RC ଅଙ୍କନ କର ।
(d) R͞C ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ R͞B କୁ A ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(e) A͞C ଅଙ୍କନ କରି Δ ABC ସଂପୂର୍ଣ୍ଣ କର ।
(f) A ବିନ୍ଦୁରେ BC ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{ZY}}\) ଅଙ୍କନ କର ।
(g) \(\overrightarrow{\mathrm{CB}}\) ଉପରେ L ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି C – B – D ଏବଂ BC = BD ହେବ ।
(h) DC ର D ବିନ୍ଦୁରେ ଅଙ୍କିତ ଲମ୍ବ \(\overleftrightarrow{\mathrm{YZ}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(i) Δ MDC ଆବଶ୍ୟକୀୟ ସମକୋଣୀ ତ୍ରିଭୁଜ ଯାହାର କ୍ଷେତ୍ରଫଳ Δ ABC ର କ୍ଷେତ୍ରଫଳର ଦୁଇଗୁଣ ।
ବି.ଦ୍ର. : Δ ABC ର ଦ୍ବିଗୁଣ ଉଚ୍ଚତା ଏବଂ ସମଭୂମିନେଇ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କରାଯାଇପାରେ ।
Question 6.
Δ ABC ଅଙ୍କନ କରି ଯାହାର m∠A = 60°, a = 7 ସେ.ମି. ଓ b – c = 4 ସେ.ମି. । ଏହାର ଅର୍ଦ୍ଧେକ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
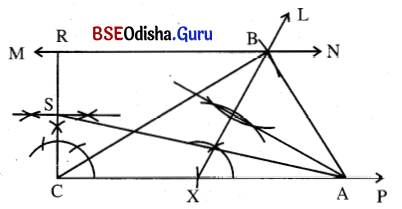
(a) \(\overrightarrow{\mathrm{CP}}\) ଅଙ୍କନ କରି ଏହା ଉପରିସ୍ଥ X ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି CX = 4 ସେ.ମି. ।
(b) X ବିନ୍ଦୁରେ ∠LXP ଅଙ୍କନ କର ଯାହାର ପରିମାଣ 60° ।
(c) C କୁ କେନ୍ଦ୍ର ଏବଂ 7 ସେ.ମି. (CB) ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ \(\overrightarrow{\mathrm{XL}}\) କୁ B ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(d) XB ର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ \(\overrightarrow{\mathrm{CX}}\) କୁ A ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(e) AB ଅଙ୍କନ କରି Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(f) AC ସହ ସମାନ୍ତର କରି B ବିନ୍ଦୁରେ \(\overleftrightarrow{\mathrm{MN}}\) ଅଙ୍କନ କର ।
(g) C ବିନ୍ଦୁରେ ଅଙ୍କିତ ଲମ୍ବ \(\overleftrightarrow{\mathrm{MN}}\) କୁ R ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(h) CR ର ମଧ୍ୟବିନ୍ଦୁ S ସ୍ଥିର କରି S͞A ଅଙ୍କନ କର ।
(i) Δ SCA ଆବଶ୍ୟକୀୟ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
ବି.ଦ୍ର. : Δ ABC ର CA ର ଅର୍ଦ୍ଧେକକୁ ଭୂମି ଏବଂ ସମ ଉଚ୍ଚତା ନେଇ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କରାଯାଇପାରେ ।
![]()
Question 7.
Δ ABC ଅଙ୍କନ କର ଯାହାର AC – AB = 2 ସେ.ମି., m∠B = 60° ଏବଂ BC = 7 ସେ.ମି. । ଏହାର କ୍ଷେତ୍ରଫଳର ଦୁଇଗୁଣ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
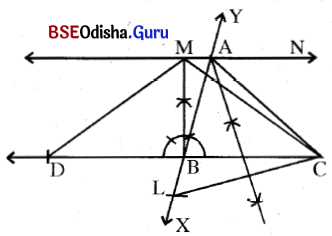
(a) 7 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ B͞C ଅଙ୍କନ କର ।
(b) BC ର B ବିନ୍ଦୁରେ ∠YBC ଅଙ୍କନ କର ଯାହାର ପରିମାଣ 60°ହେବ ।
(c) \(\overrightarrow{\mathrm{BY}}\) ର ବିପରୀତ ରଶ୍ମି \(\overrightarrow{\mathrm{BX}}\) ଉପରେ L ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି BL = 2 ସେ.ମି. ହେବ ।
(d) L͞C ଅଙ୍କନ କର । LC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ \(\overrightarrow{\mathrm{BY}}\) କୁ A ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(e) A͞C ଅଙ୍କନ କରି Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(f) \(\overrightarrow{\mathrm{CB}}\) ଉପରେ D ଏକ ବିନ୍ଦୁ ଯେପରିକି C – B – D ଏବଂ CB = BD ।
(g) A ବିନ୍ଦୁରେ B͞C ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{MN}}\) ଅଙ୍କନ କର ।
(h) B ବିନ୍ଦୁରେ ଅଙ୍କିତ ଲମ୍ବ \(\overleftrightarrow{\mathrm{MN}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(i) M͞D ଓ M͞C ଅଙ୍କନ କରି Δ MDC ତ୍ରିଭୁଜ ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 8.
Δ ABC ର BC = 5.4 ସେ.ମି., b + c = 8.7 ସେ.ମି. ଓ m∠A = 60° । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରି ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
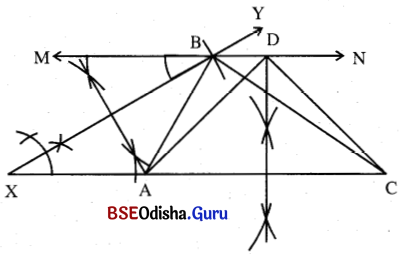
(a) 8.7 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ XC ଅଙ୍କନ କର ।
(b) XC ର X ବିନ୍ଦୁରେ ∠YXC ଅଙ୍କନ କର ଯାହାର ପରିମାଣ 30° ହେବ ।
(c) C କୁ କେନ୍ଦ୍ରକରି 5.4 ସେ.ମି. ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ଚାପ \(\overrightarrow{\mathrm{XY}}\) କୁ B ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(d) BC ଅଙ୍କନ କର । BX ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ XC କୁ A ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(e) AB ଅଙ୍କନ କରି Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(f) B ବିନ୍ଦୁରେ XC ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{MN}}\) ଅଙ୍କନ କର ।
(g) AC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ \(\overleftrightarrow{\mathrm{MN}}\) କୁ D ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(h) DA ଓ DC ଅଙ୍କନ କରି Δ DAC ଆବଶ୍ୟକୀୟ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 9.
Δ ABC ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ଭୂମି BC ଓ A ବିନ୍ଦୁରୁ B͞C ପ୍ରତି ଲମ୍ବ A͞D । BC = 5.6 ସେ.ମି. ଓ AC – AD = 3 ସେ.ମି. ନେଇ Δ ABC ଅଙ୍କନ କର ଏବଂ ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
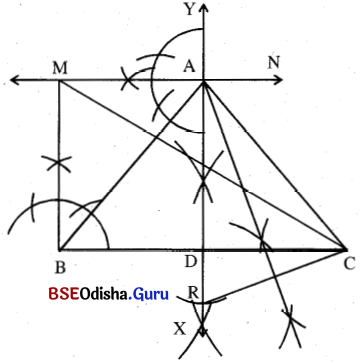
(a) 5.6 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ BC ଅଙ୍କନ କର ।
(b) BC ର ସମର୍ଦ୍ଦିଖଣ୍ଡକ ଲମ୍ବ \(\overleftrightarrow{\mathrm{XY}}\) ଅଙ୍କନ କର । BC ର ମଧ୍ୟବିନ୍ଦୁର ନାମ D ହେଉ ।
(c) \(\overrightarrow{\mathrm{DX}}\) ଉପରିସ୍ଥ R ଏକ ବିନ୍ଦୁ ଯେପରିକି DR = 3 ସେ.ମି. ।
(d) R͞C ଅଙ୍କନ କର । RC ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ \(\overleftrightarrow{\mathrm{XY}}\) କୁ A ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(e) AB ଓ AC ଅଙ୍କନ କରି Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(f) A͞D ର A ବିନ୍ଦୁରେ \(\overleftrightarrow{\mathrm{MN}}\) ଅଙ୍କନ କର ଯାହା BC ସହ ସମାନ୍ତର ହେବ ।
(g) BC ର B ବିନ୍ଦୁରେ BM ଲମ୍ବ ଅଙ୍କନ କର ।
(h) MC ଅଙ୍କନ କରି Δ MBC ଆବଶ୍ୟକୀୟ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ସମକୋଣୀ ତ୍ରିଭୁଜ ସଂପୂର୍ଣ୍ଣ କର ।
Question 10.
ଗୋଟିଏ ସମକୋଣୀ ସମଙ୍ଗିବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା 12 ସେ.ମି. । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରି ତାହାର ସମକୋଣ ସଂଲଗ୍ନ ଯେକୌଣସି ବାହୁ ଉପରେ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଗୋଟିଏ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
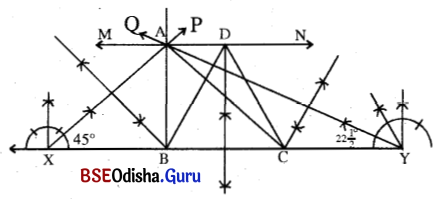
(a) 12 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ XY ଅଙ୍କନ କର ।
(b) X ଓ Y ବିନ୍ଦୁରେ ∠PXY ଓ ∠QYX ଅଙ୍କନ କର ଯାହାର ପରିମାଣ ଯଥାକ୍ରମେ 45° ଏବଂ 22 \(\frac{1}{2}\)°
(c) \(\overrightarrow{\mathrm{XP}}\) ଓ \(\overrightarrow{\mathrm{YQ}}\) ର ଛେଦବିନ୍ଦୁର ନାମ A ହେଉ ।
AX ଓ AY ର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ XY କୁ ଯଥାକ୍ରମେ B ଓ C ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(d) A͞B ଓ A͞C ଅଙ୍କନ କରି Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(e) A͞B ର A ବିନ୍ଦୁରେ BC ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{MN}}\) ଅଙ୍କନ କର ।
(f) BC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ \(\overleftrightarrow{\mathrm{MN}}\) କୁ D ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(g) B͞D ଓ D͞C ଅଙ୍କନ କରି ଆବଶ୍ୟକୀୟ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ସମଦ୍ବିବାହୁ Δ DBC ସମ୍ପୂର୍ଣ୍ଣ କର ।
![]()
Question 11.
ABCD ଚତୁର୍ଭୁଜ ଅଙ୍କନ କର ଯାହାର AB = 5 ସେ.ମି., AC = 7.2 ସେ.ମି., AD = 6 ସେ.ମି., BC = 6.2 ସେ.ମି.
ଓ CD = 5.4 ସେ.ମି. । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
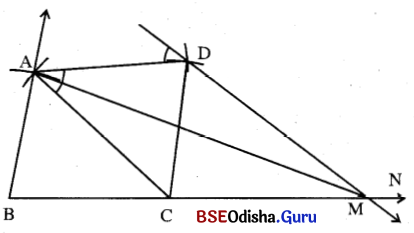
(a) AB = 5 ସେ.ମି., AC = 7.2 ସେ.ମି., ଓ BC = 6.2 ସେ.ମି. ନେଇ Δ ABC ଅଙ୍କନ କର ।
(b) A ଓ C କୁ କେନ୍ଦ୍ରକରି ଯଥାକ୍ରମେ 6 ସେ.ମି. ଓ 5.4 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଦୁଇଟି ପୃଥକ୍ ଚାପ ଅଙ୍କନ କର । ଚାପଦ୍ଵୟର ଛେଦବିନ୍ଦୁର ନାମ D ହେଉ ।
(c) A͞D ଓ DC ଅଙ୍କନ କରି ABCD ଚତୁର୍ଭୁଜ ସମ୍ପୂର୍ଣ କର ।
(d) D ବିନ୍ଦୁରେ AC ସହ ଅଙ୍କିତ ସମାନ୍ତର ସରଳରେଖା \(\overrightarrow{\mathrm{BC}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(e) AM ଅଙ୍କନ କରି ଆବଶ୍ୟକୀୟ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ Δ ABM ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 12.
ABCD ଚତୁର୍ଭୂଜ ଅଙ୍କନ କର ଯେପରି AB = 5 ସେ.ମି., BC = 7 ସେ.ମି., CD = 9 ସେ.ମି., DA = 10 ସେ.ମି. ଏବଂ m∠ABC = 120° ।
(i) ଚତୁର୍ଭୁଜର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ Δ PBC ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
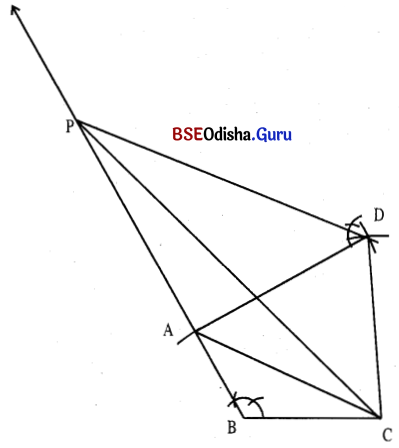
(a) AB = 5 ସେ.ମି., BC = 7 ସେ.ମି. ଓ m∠ABC = 120° ନେଇ Δ ABC ଅଙ୍କନ କର ।
(b) A ଓ C କୁ କେନ୍ଦ୍ରକରି ଯଥାକ୍ରମେ 10 ସେ.ମି. ଓ 9 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଦୁଇଟି ପୃଥକ୍ ଚାପ ଅଙ୍କନ କର । ଚାପଦ୍ଵୟର ଛେଦବିନ୍ଦୁ D ହେଉ ।
(c) AD ଓ D͞C ଅଙ୍କନ କରି ଚତୁର୍ଭୁଜ ABCD ସମ୍ପୂର୍ଣ୍ଣ କର ।
(d) AC ଅଙ୍କନ କର ।
(e) D ବିନ୍ଦୁରେ AC ସହ ଅଙ୍କିତ ସମାନ୍ତର ସରଳରେଖା \(\overrightarrow{\mathrm{BA}}\) କୁ P ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(f) P͞C ଅଙ୍କନ କରି Δ PBC ସଂପୂର୍ଣ୍ଣ କର ।
(ii) ଉପରୋକ୍ତ ମାପ ନେଇ ଚତୁର୍ଭୁଜର ଭିନ୍ନ ଏକ ଚିତ୍ର ଅଙ୍କନ କର ଓ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ Δ BDP ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
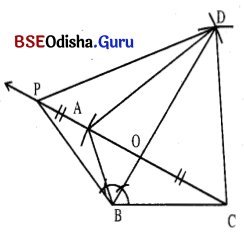
(a) ABCD ଆବଶ୍ୟକୀୟ ଚତୁର୍ଭୁଜ ଅଙ୍କନ କର ।
(b) C͞A ଓ BD କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁ O ହେଉ ।
(c) \(\overrightarrow{\mathrm{BD}}\) ଅଙ୍କନ କର ।
(d) A କୁ କେନ୍ଦ୍ରକରି CO ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଚାପ ଅଙ୍କନ କର ଏବଂ ଯେଉଁ ବିନ୍ଦୁରେ ଉକ୍ତ ଚାପ \(\overrightarrow{\mathrm{CA}}\) କୁ ଛେଦ କରିବ ତା’ର ନାମ ଦିଅ P ।
(e) B͞P ଓ PD ଅଙ୍କନ କର ।
(f) ଆବଶ୍ୟକୀୟ ତ୍ରିଭୁଜ ହେଉଛି Δ PBD ।
