BSE Odisha 9th Class Maths Solutions Geometry Chapter 7 ତ୍ରିକୋଣମିତି Ex 7(a)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 7 ତ୍ରିକୋଣମିତି Ex 7(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 7 ତ୍ରିକୋଣମିତି Ex 7(a)

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) sin θ × cot θ = ______ [cos θ, tan θ, sec θ]
ସମାଧାନ:
cos θ

(ii) cos θ × tan θ = ______ [sin θ, cosec θ, cot θ]
ସମାଧାନ:
sin θ

(iii) sin θ × sec θ × cot θ = ______ [tan θ, cosec θ, 1]
ସମାଧାନ:
1

(iv) cos θ × cosec θ × tan θ = ______ [1, cot θ, sec θ]
ସମାଧାନ:
1

(v) tan θ = 1 ହେଲେ tan θ + cot θ = ______ [1, 2, sin θ . cos θ]
ସମାଧାନ:
2

(vi) tan² θ + cot² θ – (cosec² θ + sec² θ) = ______ [1, -1, -2]
ସମାଧାନ:
-2

(vii) ABC ସମକୋଣୀ Δରେ m∠B = 90° ଓ AB = 3, BC = 4 ହେଲେ sin C = ______ [\(\frac{3}{5}\), \(\frac{4}{5}\), 1]
ସମାଧାନ:
\(\frac{3}{5}\)

(viii) ABC ସମକୋଣୀ Δରେ m∠B = 90° ଓ AB = 5, BC = 12 ହେଲେ cos A = ______ [1, \(\frac{5}{13}\), \(\frac{12}{13}\)]
ସମାଧାନ:
\(\frac{5}{13}\)

(ix) sin x = ______ (\(\sqrt{1-\cos ^2 x}, \sqrt{\cos ^2 x-1}, \sqrt{1-\cos x}, \sqrt{\cos x-1}\))
ସମାଧାନ:
\(\sqrt{1-\cos ^2 x}\)

(x) sec x = ______ (\(\sqrt{1-\tan ^2 x}, \sqrt{\tan ^2 x-1}, \sqrt{1+\tan ^2 x}, \sqrt{1+\tan x}\))
ସମାଧାନ:
\(\sqrt{1+\tan ^2 x}\)

Question 2.
ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ପ୍ରଦାନ କର ।
(i) sin α କୁ cot α ରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:
sin α = \(\frac{1}{{cosec} \alpha}\) = \(\frac{1}{\sqrt{1+\cot ^2 \alpha}}\)

(ii) cos α କୁ tan α ରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:
cos α = \(\frac{1}{{sec} \alpha}\) = \(\frac{1}{\sqrt{1+\tan ^2 \alpha}}\)

(iii) cosec α କୁ sec α ରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:

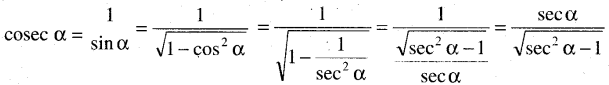
(iv) sec α କୁ cosec α ରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:

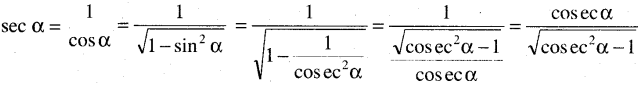
Question 3.
ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ପ୍ରଦାନ କର ।
(i) sin α = \(\frac{3}{5}\) ହେଲେ cos α × cot α ର ମାନ କେତେ ?
ସମାଧାନ:

(ii) cos α = \(\frac{4}{5}\) ହେଲେ sin α × tan α ର ମାନ କେତେ ?
ସମାଧାନ:

(iii) tan α = \(\frac{5}{12}\) ହେଲେ cot α × cosec α ର ମାନ କେତେ ?
ସମାଧାନ:

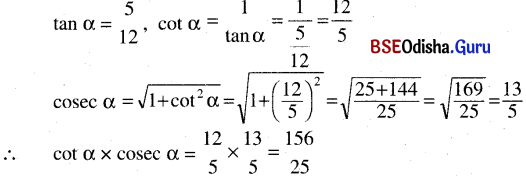
(iv) cot α = \(\frac{5}{12}\) ହେଲେ tan α × sec α ର ମାନ କେତେ ?
ସମାଧାନ:

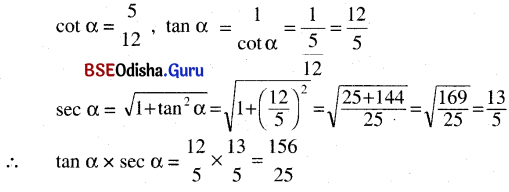
Question 4.
cosec θ = √2 ହେଲେ, ଅନ୍ୟ ପାଞ୍ଚଗୋଟି ଅନୁପାତର ମୂଲ୍ୟ କେତେ ?
ସମାଧାନ:

Question 5.
tan θ = 1 ହେଲେ, ଅନ୍ୟ ପାଞ୍ଚଗୋଟି ଅନୁପାତର ମୂଲ୍ୟ କେତେ ?
ସମାଧାନ:
tan θ = 1

Question 6.
cot θ = √3 ହେଲେ, ଅନ୍ୟ ପାଞ୍ଚଗୋଟି ଅନୁପାତର ମୂଲ୍ୟ କେତେ ?
ସମାଧାନ:

Question 7.
Δ ABC ରେ m∠A = 90°, AB = 20 ସେ.ମି. ଓ AC = 21 ସେ.ମି. ହେଲେ sin B, cos C ଓ tan B ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

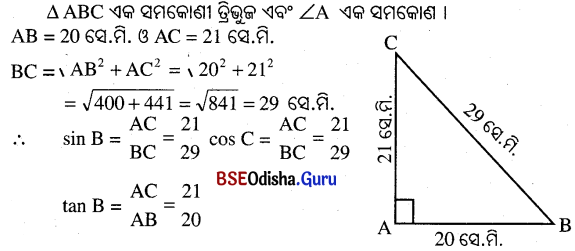
Question 8.
cot θ = \(\frac{3}{5}\) ହେଲେ, (sin θ – cos θ) ÷ (2 tan θ) ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

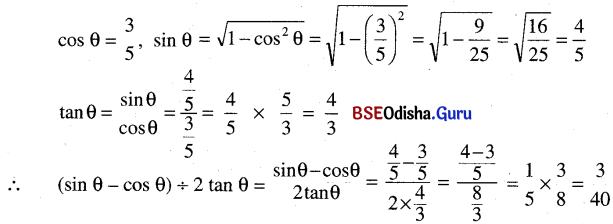
Question 9.
cot θ = \(\frac{40}{41}\) ହେଲେ, tan θ ÷ (1 – tan² θ) ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

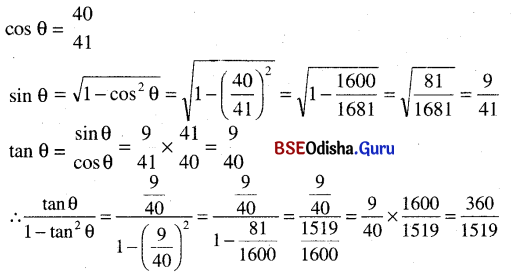
Question 10.
tan θ = \(\frac{a}{b}\) ହେଲେ, (cos θ + sin θ) ÷ (cos θ – sin θ) ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

Question 11.
tan θ = \(\frac{\sqrt{3}-1}{\sqrt{3}+1}\) ହେଲେ, sin θ + cos θ ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

ବିକଳ୍ପ ସମାଧାନ:

Question 12.
sin β = \(\frac{m}{\sqrt{m^2+n^2}}\) ହେଲେ, tan β ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

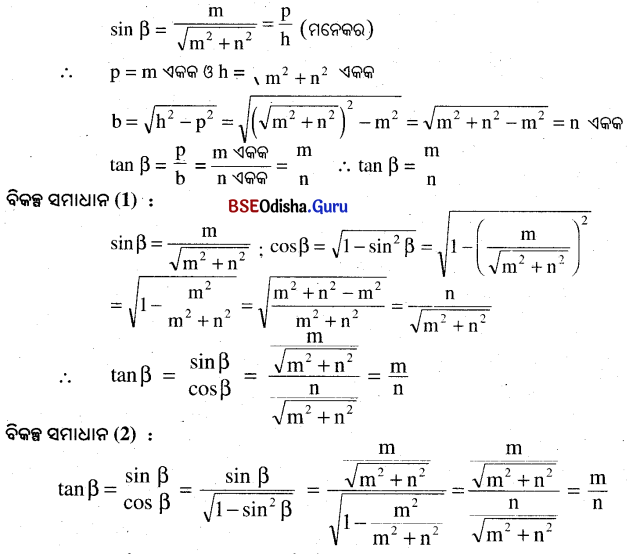
Question 13.
sin A = \(\frac{1}{2}\) ହେଲେ, cot A + \(\frac{\sin A}{1+\cos A}\) ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:
sin A = \(\frac{1}{2}\)

Question 14.
Δ ABC ରେ m∠C = 90°, BC = 20 ସେ.ମି. ଓ tan B = \(\frac{1}{4}\) ହେଲେ, AC ଓ AB ନିରୂପଣ କର ।
ସମାଧାନ:

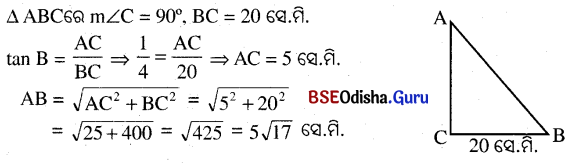
Question 15.
(sin θ + cos θ)² = 1 + 2 sin θ . cos θ
ସମାଧାନ:
L.H.S. = (sin θ + cos θ)² = sin² θ + cos² θ + 2 sin θ . cos θ
= 1 + 2 sin θ cos θ (∵ sin² θ + cos² θ = 1) = R.H.S. (ପ୍ରମାଣିତ)

Question 16.
\(\frac{1}{cosec \theta – \cot \theta}\) = cosec θ + cot θ
ସମାଧାନ:

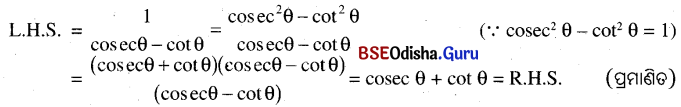
Question 17.
\(\frac{\tan ^2 \theta}{\sec \theta+1}\) = sec θ – 1
ସମାଧାନ:
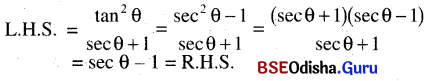 (ପ୍ରମାଣିତ)

Question 18.
\(\frac{\cos A}{1-\sin A}\) = \(\frac{1+\sin A}{\cos A}\)
ସମାଧାନ:
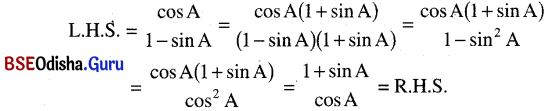(ପ୍ରମାଣିତ)

Question 19.
cot α + tan α = cosec α × sec α
ସମାଧାନ:

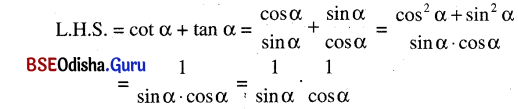
(∵ cos² a + sin² a = 1)
= cosec α × sec α = R.H.S (ପ୍ରମାଣିତ)

Question 20.
cos⁴ θ – 2cos² θ + 1 = sin⁴ θ
ସମାଧାନ:
L.H.S. = cos⁴ θ – 2cos² θ + 1 = 1 + cos⁴ θ – 2cos² θ
= (1)² + (cos² θ)² – 2 . 1 . cos² θ = (1 – cos² θ)² = (sin² θ)²
= sin⁴ θ = R.H.S. (ପ୍ରମାଣିତ)

Question 21.
cos⁴ θ – sin⁴ θ = 1 – 2sin² θ
ସମାଧାନ:
L.H.S. = cos⁴ θ – sin⁴ θ = (cos² θ)² – (sin² θ)²
= (cos² θ + sin² θ)(cos² θ – sin² θ)
= cos² θ – sin² θ (∵ cos² θ + sin² θ = 1)
= 1 – sin² θ – sin² θ
= 1 – 2sin² θ = R.H.S. (ପ୍ରମାଣିତ)

Question 22.
\(\frac{1}{1-\sin \theta}+\frac{1}{1+\sin \theta}\) = 2 sec² θ
ସମାଧାନ:
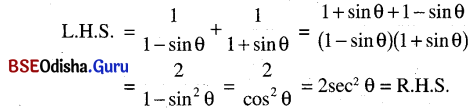(ପ୍ରମାଣିତ)

Question 23.
\(\frac{1-\tan ^3 \theta}{1-\tan \theta}\) = sec² θ + tan θ
ସମାଧାନ:

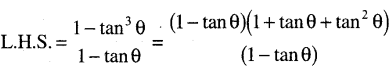
(∵ a³ – b³ = (a – b)(a² + ab + b²)
= 1 + tan² θ + tan θ
= sec² θ + tan θ = R.H.S (ପ୍ରମାଣିତ)

Question 24.
\(\frac{2 \tan \theta}{1+\tan ^2 \theta}\) = 2 sin θ . cos θ
ସମାଧାନ:
(ପ୍ରମାଣିତ)

Question 25.
\(\frac{2 \cos ^2 \theta-1}{\cot \theta-\tan \theta}\) = sin θ . cos θ
ସମାଧାନ:
(ପ୍ରମାଣିତ)

Question 26.
\(\frac{\sin ^2 \theta}{1+\cos \theta}+\frac{\sin ^2 \theta}{1-\cos \theta}\) = 2
ସମାଧାନ:

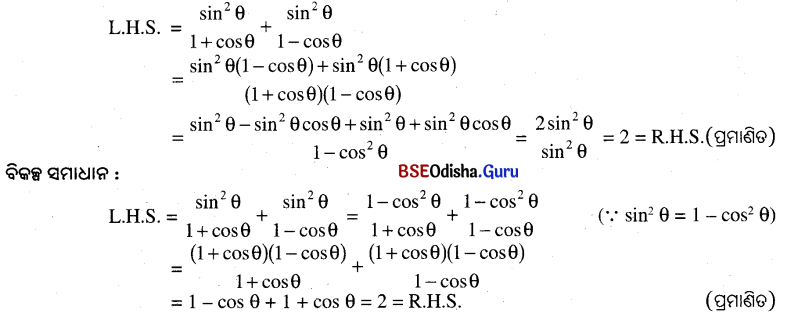
Question 27.
\(\frac{1+\sin \theta}{1-\sin \theta}+\frac{1-\sin \theta}{1+\sin \theta}\) – 4 tan² θ = 2
ସମାଧାନ:

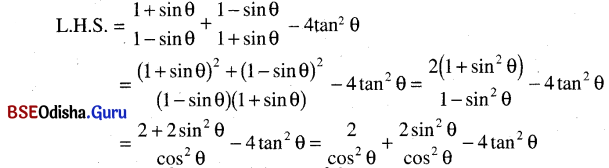
= 2 sec² θ + 2 tan² θ – 4 tan² θ
= 2 (sec² θ – tan² θ) = 2 = R.H.S. (∵ sec² θ – tan² θ = 1) (ପ୍ରମାଣିତ)

ବିକଳ୍ପ ସମାଧାନ:

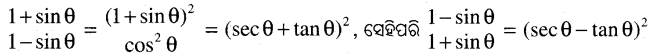
L.H.S. = (sec θ + tan θ)² + (sec θ – tan θ)² – 4 tan² θ
= 2(sec² θ + tan² θ) – 4 tan² θ
= 2sec² θ + 2tan² θ – 4 tan² θ
= 2sec² θ – 2tan² θ
= 2(sec² θ – tan² θ) = 2 = R.H.S. (ପ୍ରମାଣିତ)

Question 28.
\(\frac{1}{1+\tan ^2 \theta}+\frac{1}{1+\cot ^2 \theta}\) = 1
ସମାଧାନ:
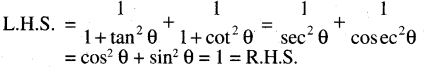(ପ୍ରମାଣିତ)

Question 29.
\(\frac{1}{1+\cos ^2 \theta}+\frac{1}{1+\sec ^2 \theta}\) = 1
ସମାଧାନ:
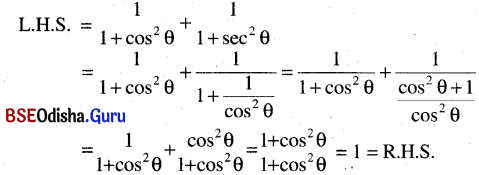(ପ୍ରମାଣିତ)

Question 30.
\(\sqrt{\frac{1+\sin \theta}{1-\sin \theta}}+\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}\) = 2 sec θ
ସମାଧାନ:
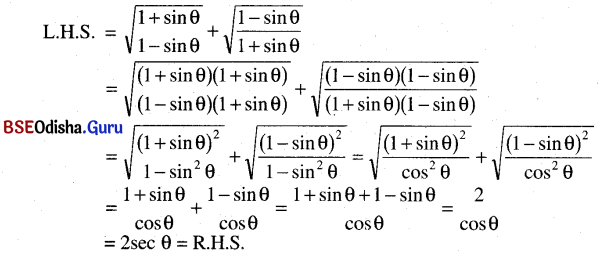(ପ୍ରମାଣିତ)

Question 31.
\(\frac{cosecA}{{cosec} A-1}+\frac{cosecA}{{cosec} A+1}\) = 2 sec² A
ସମାଧାନ:
(ପ୍ରମାଣିତ)

Question 32.
cot² θ + \(\frac{1}{\sin ^2 \theta}\) + 1 = 0
ସମାଧାନ:
L.H.S = cot² θ + \(\frac{1}{\sin ^2 \theta}\) + 1
= cot² θ – cosec² θ + 1
= 1 – cosec² θ + cot² θ
= 1 – (cosec² θ – cot² θ) (∵ cosec² θ – cot² θ = 1)
= 1 – 1 = 0 = R.H.S (ପ୍ରମାଣିତ)

Question 33.
sec A(1 + sin A)(sec A – tan A) = 1
ସମାଧାନ:
L.H.S. = sec A(1 + sin A)(sec A – tan A)
= (sec A + sec A . sin A)(sec A – tan A)
= (sec A + \(\frac{1}{\cos {A}}\) . sin A)(sec A – tan A)
= (sec A + tan A)(sec A – tan A)
= sec² A – tan² A = 1 = R.H.S. (ପ୍ରମାଣିତ)

Question 34.
(cosec α – sin α)(sec α – cos α)(tan α + cot α) = 1
ସମାଧାନ:
L.H.S = (cosec α – sin α)(sec α – cos α)(tan α + cot α) = 1
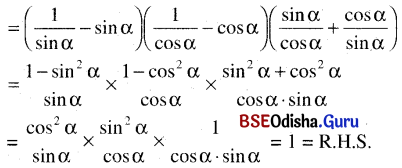(ପ୍ରମାଣିତ)

Question 35.
\(\frac{1+sin θ}{1-sin θ}\) = (sec θ + tan θ)²
ସମାଧାନ:

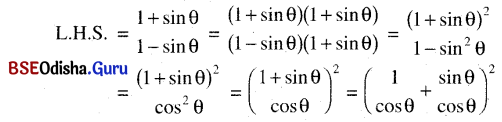
= (sec θ + tan θ)² = R.H.S. (ପ୍ରମାଣିତ)

Question 36.
tan² A . sec² B – sec² A . tan² B = tan² A – tan² B
ସମାଧାନ:
L.H.S. = tan² A . sec² B – sec² A . tan² B
= tan² A( 1 + tan² B) – ( 1 + tan² A)tan² B
= tan² A + tan² A . tan² B – tan² B – tan² A – tan² B
= tan² A – tan² B = R.H.S. (ପ୍ରମାଣିତ)

Question 37.
tan θ + sin θ = m ଓ tan θ – sin θ = n ହେଲେ ପ୍ରମାଣ କର ଯେ m² – n² = 4 √mn
ସମାଧାନ:
tan θ + sin θ = m … (i)
tan θ – sin θ = n … (ii)
ସମୀକରଣ (i) ଓ (ii) କୁ ଯୋଗକଲେ, 2 tan θ = m + n
⇒ tan θ = \(\frac{m+n}{2}\)
ସମୀକରଣ (i) ରୁ (ii) କୁ ବିୟୋଗ କଲେ, 2 sin θ = m – n
⇒ sin θ = \(\frac{m-n}{2}\)
∴ L.H.S. = m² – n² = (m + n)(m – n) = 2 tan θ × 2 sin θ
= 4 tan θ × sin θ

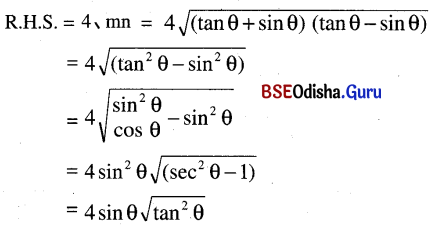
= 4 sin θ × tan θ = L.H.S.
∴ L.H.S. = R.H.S. (ପ୍ରମାଣିତ)

Question 38.
x = a sin θ ଓ y = b tan θ ହେଲେ ପ୍ରମାଣ କର ଯେ \(\frac{a^2}{x^2}-\frac{b^2}{y^2}\) = 1
ସମାଧାନ:

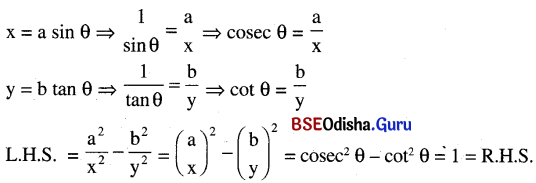
L.H.S. = R.H.S. (ପ୍ରମାଣିତ)

Question 39.
x = a cos θ + b sin θ ଓ y = a sin θ – b cos θ ହେଲେ ପ୍ରମାଣ କର ଯେ x² + y² = a² + b²
ସମାଧାନ:
x = a cos θ + b sin θ, y = a sin θ – b cos θ
L.H.S. = x² + y² = (a cos θ + b sin θ)² + (a sin θ – b cos θ)²
= a² cos² θ + b² sin² θ + 2ab cos θ . sin θ + a² sin² θ + b² cos² θ – 2ab sin θ . cos θ
= a² cos² θ + a² sin² θ + b² sin² θ + b² cos² θ
= a²(cos² θ + sin² θ) + b²(sin² θ + cos² θ) = a² + b² = R.H.S.
L.H.S. = R.H.S. (ପ୍ରମାଣିତ)

Question 40.
ଯଦି sin θ + sin² θ = 1 ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ cos² θ + cos⁴ θ = 1
ସମାଧାନ:
sin θ + sin² θ = 1
⇒ sin θ = 1 – sin² θ
⇒ sin θ = cos² θ
⇒ sin² θ = (cos² θ)²
⇒ sin² θ = cos⁴ θ
⇒ 1 – cos² θ = cos⁴ θ
⇒ cos² θ + cos⁴ θ = 1 (ପ୍ରମାଣିତ)