BSE Odisha 9th Class Physical Science Notes Chapter 5 ଗତି

Odisha State Board BSE Odisha 9th Class Physical Science Notes Chapter 5 ଗତି will enable students to study smartly.

BSE Odisha Class 9 Physical Science Notes Chapter 5 ଗତି

→ ଉପକ୍ରମ (Introduction):
(i) ବସ୍ତୁର ଅବସ୍ଥାନରେ ପରିବର୍ତ୍ତନ ଘଟିଲେ ବସ୍ତୁ ଗତି କରୁଛି ବୋଲି କୁହାଯାଏ ।
(ii) ଗୋଟିଏ ସ୍ଥିର ବସ୍ତୁକୁ ଭିଭିକରି ଅନ୍ୟ ଗୋଟିଏ ବସ୍ତୁର ଅବସ୍ଥିତି ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

→ ବିଶ୍ରାମ ଏବଂ ଗତି (Rest and Motion):
(i) ଘର, ବାଡ଼ି, ଗଛଲତା, ପାହାଡ଼ ପର୍ବତ, ନଦୀ, ନାଳ ଓ ସମୁଦ୍ର ଆଦିକୁ ସ୍ଥିର ବସ୍ତୁ କୁହାଯାଏ; କାରଣ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିନ୍ଦୁଠାରୁ ସେମାନଙ୍କର ଅବସ୍ଥାନର ପରିବର୍ତ୍ତନ ହୋଇ ନଥାଏ ।
(ii) ରାସ୍ତାଘାଟରେ ଯା’ଆସ କରୁଥିବା ଯାନବାହନ, ମନୁ ଷ୍ୟ, ନଈ, ନାଳ, ଝରଣା ଇତ୍ୟାଦିରେ ବହିଯାଉଥ‌ିବା ପାଣି; ପାଣିରେ ପହଁରୁଥ‌ିବା ମାଛ ଓ ହଂସ, ଅକାଶରେ ଉଡୁଥ‌ିବା ପକ୍ଷୀ ଆଦିକୁ ଗତିଶୀଳ କୁହାଯାଏ ।
(iii) କେତେକ କ୍ଷେତ୍ରରେ ଗତିକୁ ପରୋକ୍ଷ ଭାବରେ ଜାଣିହୁଏ ।

ଉଦାହରଣ :
(a) ବାଲିକଣା ଉଡ଼ିଲେ ତାହାର ଗତିରୁ ବାୟୁର ଗତି ଜଣାପଡ଼େ ।
(b) ବାଲିକଣା ଉଡ଼ିଲେ ତାହାର ଗତିରୁ ବାୟୁର ଗତି ଜଣାପଡ଼େ ।
(c) ସୂର୍ଯ୍ୟୋଦୟ ଓ ସୂର୍ଯ୍ୟାସ୍ତ ଏବଂ ଋତୁ ପରିବର୍ତ୍ତନ ପୃଥ‌ିବୀର ଗତି ଯୋଗୁଁ ହୋଇଥାଏ । କିନ୍ତୁ ପୃଥ‌ିବୀର ଗତିକୁ ଦେଖୁହୁଏ ନାହିଁ ।
(iv) ଅନ୍ୟ କ୍ଷେତ୍ରରେ ଗୋଟିଏ ବସ୍ତୁ ଜଣକୁ ଗତିଶୀଳ ଜଣାଯାଉଥିଲେ ମଧ୍ୟ ଆଉ ଜଣକୁ ତାହା ସ୍ଥିର ବୋଲି ସବୁ ପୃଥ‌ିବୀର ଗତିକୁ ଦେଖୁହୁଏ ନାହିଁ ଗତି କରୁଥିବାର ଦେଖେ କିନ୍ତୁ ବସ୍‌ରେ ଯାଉଥିବା ତା’ର ସହଯାତ୍ରୀମାନଙ୍କୁ ସ୍ଥିର ଥିବାର ଦେଖେ ।
(v) ବସ୍ତୁର ଅବସ୍ଥାନର ପରିବର୍ତ୍ତନ ହେଲେ, ତାହାକୁ ଗତିଶୀଳ ବୋଲି କୁହାଯାଏ ।
(i) ବସ୍ତୁର ବିଭିନ୍ନ ପ୍ରକାର ଗତି ଥାଏ; ଯଥା-ସରଳରୈଖ୍ୟକ ଗତି, ଘୂର୍ଣ୍ଣନ ଗତି, ଦୋଳନ ଗତି, କମ୍ପନ ଗତି ଇତ୍ୟାଦି ।
(ii) ସଳଖ ପଥରେ ଗତି କରୁଥିବା ବସ୍ତୁଗୁଡ଼ିକୁ ସରଳରେଖକ ଗତି କୁହାଯାଏ ।

ବସ୍ତୁର ଅବସ୍ଥାନ : ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ସ୍ଥିର ବିନ୍ଦୁଠାରୁ ବସ୍ତୁର ଅବସ୍ଥାନକୁ ଏହାର ଦୂରତା କୁହାଯାଏ । ଏହି ବିନ୍ଦୁକୁ ମୂଳ ବିନ୍ଦୁ କୁହାଯାଏ । ମୂଳ ବିନ୍ଦୁକୁ ନେଇ ବସ୍ତୁର ଅବସ୍ଥାନ ଜାଣିହୁଏ ।

→ ଗତି (Motion):
ସମୟ ଅନୁ ସାରେ ବସ୍ତୁର ଅବସ୍ଥାନର ପରିବର୍ତ୍ତନକୁ ବସ୍ତୁର ଗତି କୁହାଯାଏ । ବସ୍ତୁର ଅବସ୍ଥାନ ହେଉଛି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିନ୍ଦୁଠାରୁ ଏହାର ଦୂରତା । ଏହି ବିନ୍ଦୁକୁ ନିର୍ଦ୍ଦେଶକ ବିନ୍ଦୁ (Reference point) ବା ମୂଳବିନ୍ଦୁ (origin) କୁହାଯାଏ । ଏହି ମୂଳବିନ୍ଦୁକୁ ଭିଭିକରି ଅନ୍ୟ ବସ୍ତୁର ଅବସ୍ଥିତି ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

→ ଏକ ସରଳରେଖାରେ ଗତି (ସରଳରେଖକ ଗତି) (Motion along a straight line):
ବସ୍ତୁ ସରଳରେଖାରେ ଗତି କଲେ, ବସ୍ତୁର ସେହି ଗତିକୁ ସରଳରେଖ୍ୟକ ଗତି କୁହାଯାଏ ।
ଉଦାହରଣ :
ଚଟାଣରେ ବଲ୍‌ର ଗତି; ବସ୍, ଟ୍ରକ୍, ସ୍କୁଟର, ମଟର ସାଇକେଲ୍‌ର ଗତି; ଗଛରୁ ପଡୁଥିବା ଳର ଗତି ଆଦି ସରଳରେଖ୍ୟକ ଗତିର ଅନ୍ତର୍ଗତ ।

→ ଦୂରତା (Distance):
ଗୋଟିଏ ବସ୍ତୁ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ବାହାରି କୌଣସି ଏକ ପଥରେ ଗତିକରି ଅନ୍ତିମ ବିନ୍ଦୁରେ ପହଞ୍ଚିଲେ ବସ୍ତୁଟି ଅତିକ୍ରମ କରିଥିବା ପଥର ପ୍ରକୃତ ଦୈର୍ଘ୍ୟ (Length) କୁ ଦୂରତା
(i) ଦୂରତା ଏକ ଅଦିଶ ରାଶି (scalar quantity) କାରଣ ଏହାର ଦିଗ ନଥାଏ ।
(ii) ଏହି ଭୌତିକ ‘ରାଶିର ପରିମାଣକୁ କେବଳ ସଂଖ୍ୟାଦ୍ଵାରା ପ୍ରକାଶ କରାଯାଏ ।
ଏକକ : S.I. ପଦ୍ଧତିରେ ଦୂରତାର ଏକକ କି.ମି. ବା ମି. । CGS ପଦ୍ଧତିରେ ଦୂରତାର ଏକକ ସେ.ମି. ।
ଉଦାହରଣ :

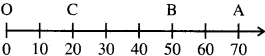
ମନେକର ଗୋଟିଏ ବସ୍ତୁ ଏକ ସରଳରେଖାରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିନ୍ଦୁ ( ଠାରୁ ତାହାର ଗତି ଆରମ୍ଭ କଲା । ଭିନ୍ନ ଭିନ୍ନ ସମୟରେ A, B ଓ C ବସ୍ତୁର ବିଭିନ୍ନ ଅବସ୍ଥାନର ତିନୋଟି ବିନ୍ଦୁ । ବସ୍ତୁଟି C ଓ B ବିନ୍ଦୁ ଦେଇ A ଆଡ଼କୁ ଯାଇଛି । ସେଠାରୁ ପୁନଶ୍ଚ ସେ B ବିନ୍ଦୁ ଦେଇ C ବିନ୍ଦୁକୁ ଫେରିଆସିଛି ।
ବସ୍ତୁଟି ଅତିକ୍ରାନ୍ତ କରିଥିବା ମୋଟ ଦୂରତା = OA+ AC = 70 କି.ମି. + 50 କି.ମି. = 120 କି.ମି.।

→ ବିସ୍ଥାପନ (Displacement):
(i) ଗୋଟିଏ ବସ୍ତୁ ଏକ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ତା’ର ଗତି ଆରମ୍ଭ କରି ଏକ ଅନ୍ତିମ ବିନ୍ଦୁରେ ପହଞ୍ଚିଲା ପରେ ସେହି ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ ଥ‌ିବା ସର୍ବନିମ୍ନ ଦୂରତାକୁ ବସ୍ତୁର ବିସ୍ଥାପନ କୁହାଯାଏ । ଅର୍ଥାତ୍ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ଅନ୍ତିମ ବିନ୍ଦୁପର୍ଯ୍ୟନ୍ତ ବସ୍ତୁର ଅତିକ୍ରମ ଦୂରତାକୁ ବିସ୍ଥାପନ କୁହାଯାଏ ।
(ii) ବିସ୍ଥାପନ ଏକ ସଦିଶ ରାଶି (Vector quantity) କାରଣ ଏହାର ଉଭୟ ପରିମାଣ ଓ ଦିଗ ରହିଥାଏ ।
(iii) ବିସ୍ଥାପନର ଦିଗ ସର୍ବଦା ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ଅନ୍ତିମ ବିନ୍ଦୁ ଆଡ଼କୁ ହୋଇଥାଏ ।

ଉଦାହରଣ :
(i) ଉପରିସ୍ଥ ଚିତ୍ରରେ ବସ୍ତୁଟି ଠ ଠାରୁ A ପର୍ଯ୍ୟନ୍ତ ଏକ ସରଳରେଖାରେ 70 କି.ମି. ଦୂରତା ଯାଇଛି । = 70 କି.ମି. ଏଠାରେ ବିସ୍ଥପନର ପରିମାଣ = ଦୂରତା = 70 କି.ମି
(ii) ବସ୍ତୁଟି ଠ ଠାରୁ A ପର୍ଯ୍ୟନ୍ତ ଯାଇ ପୁନଶ୍ଚ Bକୁ ଫେରି ଆସିଲେ ଅତିକ୍ରାନ୍ତ ଦୂରତା OA + AB = 70 କି.ମି.+ 20 କି.ମି. = 90 କି.ମି. ମାତ୍ର B ସ୍ଥାନରେ ମୂଳବିନ୍ଦୁ ( ଠାରୁ ବସ୍ତୁର ବିସ୍ଥାପନ 50 କି.ମି. । ତେଣୁ ବିସ୍ଥାପନର ପରିମାଣ (50 କି.ମି.) ଅତିକ୍ରାନ୍ତ ଦୂରତାର ପରିମାଣ (90 କି.ମି.) ସହ ସମାନ ନୁହେଁ ।
(iii) ଯଦି ବସ୍ତୁଟି ମୂଳବିନ୍ଦୁ ୦ ଠାରୁ ବାହାରି A ପର୍ଯ୍ୟନ୍ତ ଯାଇ ପୁଣି ଠ କୁ ଫେରି ଆସିଲେ, ଅତିକ୍ରାନ୍ତ ଦୂରତା = 70 କି.ମି. + 70 କି.ମି. = 140 କି.ମି. ।
କିନ୍ତୁ ବସ୍ତୁର ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁ ଓ ଅନ୍ତିମ ବିନ୍ଦୁ ସମାନ ହୋଇଯିବାରୁ ବସ୍ତୁର ବିସ୍ଥାପନ ଶୂନ ହେବ ।

• ଗୋଟିଏ ବିନ୍ଦୁରେ ବସ୍ତୁର ବିସ୍ଥାପନ ଶୂନ ହୋଇପାରେ, ମାତ୍ର ଅତିକ୍ରାନ୍ତ ଦୂରତା ଶୂନ ହେବ ନାହିଁ ।
• ଦୂରତାର ଏକକ ବିସ୍ଥାପନର ଏକକ ସହ ସମାନ ।
• ମୋଟରଯାନ ଗତି କରୁଥିବାବେଳେ ଅତିକ୍ରମ କରୁଥିବା ଦୂରତା ମାପିବା ପାଇଁ ସେଥୁରେ ଓଡ଼ୋମିଟର (Odometer) ଲାଗିଥାଏ ।

→ ୟୁନିଫର୍ମ ଗତି ଏବଂ ଅଣ ୟୁନିଫର୍ମ ଗତି। (Uniform Motion & Non-Uniform Motion) :
ସମଗତି :
(i) ଗୋଟିଏ ବସ୍ତୁ ସମାନ ସମୟ ଅନ୍ତରାଳରେ ସମାନ ଦୂରତା ଅତିକ୍ରମ କଲେ, ତାହାର ଗତିକୁ ସମଗତି କୁହାଯାଏ ।
(ii) ସମଗତି କ୍ଷେତ୍ରରେ ସମୟର ଅନ୍ତରାଳ କମ୍ ହେବା ଉଚିତ । ସମଗତି କ୍ଵଚିତ୍ ଦେଖାଯାଏ ।

ଉଦାହରଣ:
ମନେକର ଗୋଟିଏ ବସ୍ତୁ ଏକ ସରଳ ପଥରେ ପ୍ରଥମ ଘଣ୍ଟାରେ 5 କି.ମି., ଦ୍ଵିତୀୟ ଘଣ୍ଟାରେ 5 କି.ମି., ତୃତୀୟ ଘଣ୍ଟାରେ 5 କି.ମି. ଏବଂ ଚତୁର୍ଥ ଘଣ୍ଟାରେ ମଧ୍ଯ 5 କି.ମି. ଦୂରତା ଅତିକ୍ରମ କରୁଛି; ଅର୍ଥାତ୍ ପ୍ରତି ଏକ ଘଣ୍ଟା ସମୟ ଅନ୍ତରାଳ (interval)ରେ ଏହା 5 କି.ମି. ଯାଉଅଛି । ଏଠାରେ ବସ୍ତର ଗତି ସମଗତି ଅଟେ ।
ଅସମ ଗତି :
(i) ଗୋଟିଏ ବସ୍ତୁ ସମାନ ସମୟ ଅନ୍ତରାଳରେ ଅସମାନ ଦୂରତା ଅତିକ୍ରମ କଲେ ତାହାର ଗତିକୁ ଅସମ’ ଗତି କୁହାଯାଏ ।
(ii) ପ୍ରକୃତିରେ ଅଧୁକାଂଶ ଗତି ଅସମ ଅଟେ ।

ଉଦାହରଣ:
(ii)ଜନଗହଳି ରାସ୍ତାରେ ଯାନର ଗତି ଓ ଉଠାଣି ବା ଗଡ଼ାଣି ସ୍ଥାନରେ ଯାନର ଗତି ଅସ ଅଟେ ।
(i) ମନେକର ଗୋଟିଏ ବସ୍ତୁ ପ୍ରଥମ ଘଣ୍ଟାରେ 5′ କି.ମି., ଦ୍ଵିତୀୟ ଘଣ୍ଟାରେ 3 କି.ମି. ଓ ତୃତୀୟ ଘଣ୍ଟାରେ 7 କି.ମି ଦୂରତା ଅତିକ୍ରମ କରୁଛି । ଏଠାରେ ପ୍ରତି ଏକ ଘଣ୍ଟା ସମୟ ଅନ୍ତରାଳରେ ଅସମାନ ଦୂରତା ଅତିକ୍ରମ କରୁଛି । ଏଠାରେ ବସ୍ତୁର ଗତି ଅସମ ଅଟେ ।

→ ଗତି (Speed):
(i) ଏକକ ସମୟ ବ୍ୟବଧାନରେ ଏକ ବସ୍ତୁ ଅତିକ୍ରାନ୍ତ କରିଥିବା ଦୂରତାକୁ ସେହି ବସ୍ତୁର ବେଗ କୁହାଯାଏ ।
(ii) ଏକ ବସ୍ତୁ t ସମୟରେ s ଦୂରତା ଅତିକ୍ରମ କଲେ, ତାହାର ବେଗ

ବେଗର ପରିମାଣ ଥାଏ କିନ୍ତୁ ଦିଗ ନଥାଏ, ତେଣୁ ଏହା ଏକ ଅଦିଶ ରାଶି ।

→ ୟୁନିଫର୍ମ ସ୍ପିଡ୍ ଏବଂ ଅଣ ୟୁନିଫର୍ମ ସ୍ପିଡ୍। (Uniform Speed and Non-Uniform Speed):
(i) ଗତିଶୀଳ ବସ୍ତୁ ସମାନ ସମୟ ଅନ୍ତରାଳରେ ସମାନ ଦୂରତା ଅତିକ୍ରମ କରୁଥିଲେ, ତାହା ସମବେଗରେ ଗତି କରୁଛି ବୋଲି କୁହାଯାଏ ।
(ii) ଗତିଶୀଳ ବସ୍ତୁ ସମାନ ସମୟ ଅନ୍ତରାଳରେ ଅସମାନ ଦୂରତା ଅତିକ୍ରମ କରୁଥିଲେ, ତାହାର ବେଗକୁ ଅସମ ବେଗ କୁହାଯାଏ । ଅସମ ବେଗରେ ଯାଉଥିବା ଗତିଶୀଳ ବସ୍ତୁର ହାରାହାରି ବେଗ ଅନେକ କ୍ଷେତ୍ରରେ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

ଯେଉଁଠି u = ବସ୍ତୁର ହାରାହାରି ବେଗ
s = ବସ୍ତୁ ଅତିକ୍ରମ କରିଥିବା ମୋଟ ଦୂରତା, t = ବସ୍ତୁ ନେଇଥ‌ିବା ମୋଟ ସମୟ

→ ପରିବେଗ (Velocity):
(i) ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ଗତିଶୀଳ ବସ୍ତୁର ବେଗକୁ ପରିବେଗ (velocity) କୁହାଯାଏ ।
(ii) ବସ୍ତୁର ଏହି ପରିବେଗ ସମପରିବେଗ କିମ୍ବା ପରିବର୍ତୀ (variable) ପରିବେଗ ହୋଇପାରେ । ବସ୍ତୁର ବେଗ କିମ୍ବା ତାହାର ଗତିର ଦିଗ କିମ୍ବା ଉଭୟର ପରିବର୍ତ୍ତନ ହେଲେ ପରିବେଗର ପରିବର୍ତ୍ତନ ହୁଏ ।
(iii) ବସ୍ତୁର ପରିବେଗ ସମୟ ଅନୁସାରେ ସମାନ ହାରରେ ପରିବର୍ତ୍ତିତ ହେଲେ :


ଯେଉଁଠାରେ v_av = ବସ୍ତୁର ହାରାହାରି ପରିବେଗ
u = ବସ୍ତୁର ପ୍ରାରମ୍ଭିକ ପରିବେଗ
v = ବସ୍ତୁର ଅନ୍ତିମ ପରିବେଗ

→ ତ୍ୱରଣ (Acceleration):
(i) ପରି ବେଗର ପରିବର୍ତ୍ତନ ହାରକୁ ତ୍ଵରଣ (Acceleration) ତ୍ଵରଣ କୁହାଯାଏ ।
କିମ୍ବା, ଏକକ ସମୟ ଅବଧ୍ଧରେ ବସ୍ତୁର ପରିବେଗର ପରିବର୍ତ୍ତନକୁ ବସ୍ତୁର ତ୍ଵରଣ କୁହାଯାଏ
(ii) ଯଦି ଗୋଟିଏ ବସ୍ତୁର ପରିବେଗ t ସମୟ ମଧ୍ୟରେ uରୁ vକୁ ପରିବର୍ତ୍ତିତ ହୁଏ, ତେବେ ତ୍ଵରଣ
(iii) ତ୍ଵରଣ ଗୋଟିଏ ସଦିଶ ରାଶି । ଏହାର ଉଭୟ ପରିମାଣ ଓ ଦିଗ ଥାଏ ।
(iv) ଗତିଶୀଳ ବସ୍ତୁର ତ୍ଵରଣ ଥିଲେ, ବସ୍ତୁର ଗତିକୁ ତ୍ୱରାନ୍ବିତ (accelerated) ଗତି କୁହାଯାଏ ।
(v) ପରିବେଗ ଦିଗରେ ତ୍ଵରଣ ହେଲେ ତାହାକୁ ଯୁକ୍ତାତ୍ମକ (Positive) ତ୍ଵରଣ ଏବଂ ପରିବେଗର ବିପରୀତ ଦିଗରେ ତ୍ଵରଣ ହେଲେ ତାହାକୁ ବିଯୁକ୍ତାତ୍ମକ ତ୍ଵରଣ ବା ମନ୍ଦନ (Retardation) କୁହାଯାଏ ।
(vi) ଏକ ସରଳରେଖାରେ ଗତି କରୁଥିବା ବସ୍ତୁର ପରିବେଗ ସମାନ ସମୟ ଅନ୍ତରାଳରେ ସମାନ ପରିମାଣରେ ବୃଦ୍ଧି କିମ୍ବା ହ୍ରାସ ପାଉଥିଲେ ବସ୍ତୁଟି ସମତ୍ଵରଣରେ ଗତି କରୁଛି ବୋଲି କୁହାଯାଏ ।
(vii) ବସ୍ତୁର ପରିବେଗ ଅସମ ହାରରେ ପରିବର୍ତ୍ତିତ ହେଲେ ତାହାର ତ୍ଵରଣ ଅସୀମ ଅଟେ ।
ଉଦାହରଣ:
ଜନଗହଳିପୂର୍ଣ୍ଣ ରାସ୍ତାରେ ଗତିଶୀଳ କାର୍‌ର ଗତି ଅସମ-ତ୍ଵରଣ ଅଟେ ।

→ ଗତିର ଲୈଖକ ବା ଗ୍ରାଫିକାଲ୍ ପରିପ୍ରକାଶ (Graphical Representation of Motion):
(i) ଆଲେଖ (Graph) ଦ୍ୱାରା ବିଭିନ୍ନ ପ୍ରକାର ଗତିର ତଥ୍ୟକୁ ସହଜରେ ଓ ସୁବିଧାରେ ଜାଣିହୁଏ ।
(ii) ରେଖା ଗ୍ରାଫ୍‌ରୁ ଗୋଟିଏ ବସ୍ତୁର ଗତି ସମ୍ପର୍କରେ ଅନେକ ତଥ୍ୟ ସହଜରେ ଜାଣିହୁଏ ।
(iii) ରେଖା ଗ୍ରାଫ୍‌ରେ ଗତିର ସାଧାରଣ ସମୟକୁ X-ଅକ୍ଷରେଖାରେ ଓ ବସ୍ତୁର ବେଗ ବା ପରିବେଗ ବା ଦୂରତା ବା ବିସ୍ଥାପନ ଇତ୍ୟାଦିକୁ Y-ଅକ୍ଷରେଖାରେ ନିଆଯାଏ । ଅନେକ କ୍ଷେତ୍ରରେ ଭୌତିକ ରାଶିଗୁଡ଼ିକୁ ଅଲଗା ଅକ୍ଷରେ ମଧ୍ୟ ନିଆଯାଏ ।
(iv) ଗ୍ରାଫ୍ ପାଇଁ ଯେଉଁ ଦୁଇଟି ରାଶିକୁ ନିଆଯାଏ ତାହା ମଧ୍ୟରୁ ସ୍ଵାଧୀନ ଚଳ (Independent variable)କୁ x-ଅକ୍ଷରେଖାରେ ଓ ନିର୍ଭରଶୀଳ ଚଳ (Dependent variable) କୁ Y-ଅକ୍ଷରେଖାରେ ନିଆଯାଇଥାଏ ।

→ ସମୟ-ଦୂରତା ଗ୍ରା ଫ୍ (Distance-Time Graph):
ବସ୍ତୁଟି ସମ-ବେଗରେ ବା ଅସମ ବେଗରେ ଗତି କରୁଥିଲେ ବା ସ୍ଥିର ହୋଇ ରହିଥିଲେ ତାହାର ସମୟ- ଦୂରତା ଗ୍ରାଫ୍ ଅଙ୍କନ କରାଯାଇ ପାରିବ ।

(a) ସମ ବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍:
(i) ମନେକର ଗୋଟିଏ ବସ୍ତୁ ସରଳରେଖାରେ ସମ ବେଗରେ ଗତି କରୁଛି । ଏହି ଗତିରେ ବସ୍ତୁଦ୍ଵାରା ଅତିକ୍ରାନ୍ତ ଦୂରତା ସମାନ ସମୟ ଅନ୍ତରାଳରେ ସମାନ ପରିମାଣରେ ବୃଦ୍ଧିପାଏ ।
(ii) ସମ ବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ତୀର୍ଯ୍ୟକ ସରଳରେଖା ହୁଏ ଓ ଏଥିରୁ ଜଣାଯାଏ ଦୂରତା ସମହାରରେ ବୃଦ୍ଧି ପାଉଛି ।
(iii) ସମୟ-ଦୂରତା ଗ୍ରାଫ୍‌ରେ ଦୁଇଟି ବିନ୍ଦୁ A ଓ B ନିଆଯାଉ । À ସ୍ଥାନରେ ସମୟର ପାଠ୍ୟଙ୍କ t₁ ଏବଂ B ସ୍ଥାନରେ ସମୟର ପାଠ୍ୟାଙ୍କ ହେଉ । A ବିନ୍ଦୁ ର ପାଠ୍ୟଙ୍କ s₁ ଏବଂ ଦୂର ତାର B ବି ନ୍ଦୁ ର s₂ ହେଉ ।

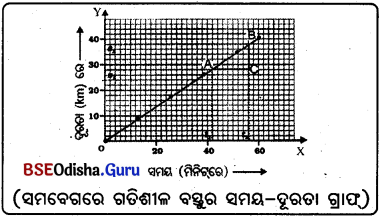
(iv) A ବିନ୍ଦୁରୁ X-ଅକ୍ଷରେଖା କରି ଅନ୍ୟ ଏକ ରେଖା ସହ ସମାନ୍ତର କରି ଏକ ରେଖା ଏବଂ B ବିନ୍ଦୁରୁ Y-ଅକ୍ଷରେଖା ସହ ସମାନ୍ତର ଟାଣ । ରେଖାଦ୍ଵୟ ପରସ୍ପରକୁ ୯ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତୁ ।
(v) ∆ ABC ରେ AC = ସମୟ ବ୍ୟବଧାନ = t₂ – t₁ ଓ BC = ଦୂରତାର ବ୍ୟବଧାନ = s₂ – S₁
 
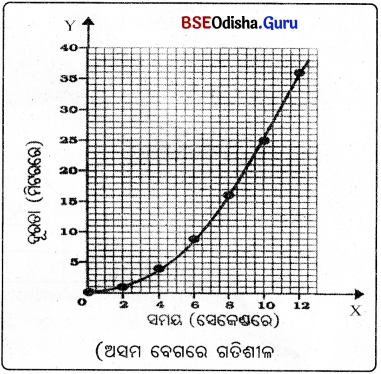
(b) ଅସମ ବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ :
(i) ଗୋଟିଏ ଗତିଶୀଳ କାରର ପ୍ରତି ଦୁଇ ସେକେଣ୍ଡ ଅନ୍ତରାଳରେ ଅତିକ୍ରାନ୍ତ ଦୂରତାକୁ ଦର୍ଶାଯାଇଛି

(ii) ଅସମ ବେଗରେ ଗତି ଶୀଳ ବସ୍ତୁଦ୍ୱାରା ଅତିକ୍ରାନ୍ତ ଦୂରତା ସମାନ ସମୟ ଅନ୍ତରା କରେ ଅପମାନ ପରିମାଣରେ ବୃଦ୍ଧି ପାଏ ।
(iii) ଏ ପ୍ରକାର ଗତି ପାଇଁ ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଏକ ବକ୍ରରେଖା ହୋଇଥାଏ । ଏହି ଗ୍ରାଫରୁ ସୂଚନା ମିଳେ ଯେ ଦୂରତା ଅସମ ହାରରେ ବୃଦ୍ଧି ପାଉଛି ।

(c) ସ୍ଥିର ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ :
ଯଦି ବସ୍ତୁ ର ଅବସ୍ଥାନ ସମୟ ଅନୁ ସାରେ ନ ବଦଳେ, ତେବେ ଗ୍ରାଫ୍‌ର ଅନୁ ରେଖ ଏକ ଭୂସମାନ୍ତର ସରଳରେଖା ହେବ ।

→ ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ (Velocity-Time Graph) : (କାରର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍)
ସମୟ- ପରିବେଗ ଗ୍ରାଫ୍‌ରେ ସମୟକୁ X-ଅକ୍ଷରେଖାରେ ଏବଂ ପରିବେଗକୁ Y-ଅକ୍ଷରେଖାରେ ନିଆଯାଏ।
(a) ସମ ପରିବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ଟ :
(i) ଯଦି ବସ୍ତୁଟି ସମ ପରିବେଗରେ ଗତି କରୁଥାଏ ତେବେ ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ ସମୟ ଅକ୍ଷରେଖା ସମାନ୍ତର ଏକ ସରଳରେଖା ସହି ତ ହୁଏ । ଏହି। ରଉଚ୍ଚତା ସମୟ ଅକ୍ଷରେଖା ସହ ପରିବର୍ତ୍ତନ ହେବ ନାହିଁ ।
(ii) ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ AB ଦ୍ଵାରା ସୂଚିତ ହୋଇଛି । ଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ ସ୍ଥିର ପରିବେଗ 40km/h ରେ ଗତି ପାଉଛି ।
(iii) A ଓ B ବିନ୍ଦୁରୁ ଦୁଇଟି ଲମ୍ବ AC ଓ BD ଅଙ୍କନ କଲେ ତାହା X-ଅକ୍ଷରେଖାକୁ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ଛେଦ କରିବ ।

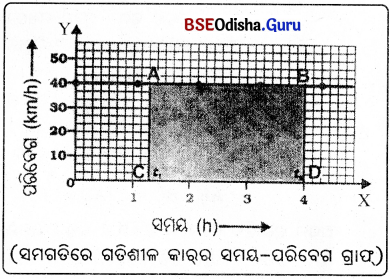
(iv) A ବିନ୍ଦୁ ଓ B ବିନ୍ଦୁଠାରେ ସମୟର ପାଠ୍ୟଙ୍କ ଯଥାକ୍ରମେ
t, ଓ t2 ହେର୍ତ୍ତ । AC = BD = 40 km/h 10° AB = CD = t₂ – t₁।
(v) କାର୍‌ଟି (t₁ – t₂) ସମୟ ମଧ୍ୟରେ ଅତିକ୍ରାନ୍ତ କରିଥିବା ଦୂରତା / ପରିବେଗକୁ s ଦ୍ଵାରା ପ୍ରକାଶ କଲେ,
ବିସ୍ଥାପନ (s) = ABDCର କ୍ଷେତ୍ରଫଳ = AC × CD

(vi) ଯଦି ବସ୍ତୁଟି ସମ ପରିବେଗରେ ଗତି କରୁଥାଏ, ତେବେ ପରିବେଗ ଓ ସମୟର ଗୁଣଫଳ ବିସ୍ଥାପନକୁ ସୂଚାଏ ।

(b) ସମ ତ୍ଵରାନ୍ଵିତ ବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ :
(i) ମନେକର ଗୋଟିଏ କାର୍ ସଳଖ ପଥରେ ସମ ତ୍ଵରାନ୍ଵିତ ବେଗରେ ଗତିକରୁଛି । ନିମ୍ନ ସାରଣୀରେ ପ୍ରତି 5 ସେକେଣ୍ଡରେ ତାହାର ଗତିକୁ m/s ଏକକରେ ଦର୍ଶାଯାଇଛି ।

(ii) ଏଠାରେ ଗତ ଶୀଳ ବସ୍ତୁର ପର ବେଗ ସମାନ ସମୟ ଅନ୍ତରାଳରେ ପରିବର୍ତ୍ତିତ ହେଉଛି । ଦତ୍ତ ସାରଣୀଦ୍ଵାରା ସୂଚିତ ସମ ତ୍ଵରାନ୍ଵିତ ଗତି ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ ଗୋଟିଏ ତୀର୍ଯ୍ୟକ୍ ସରଳରେଖା ହେବ ।
(iii) ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ ଓ ସମୟ ଅକ୍ଷ ମଧ୍ୟରେ ଦୁଇଟି ସମୟ ମୁହୂର୍ତ୍ତ ମଧ୍ୟରେ ଆବଦ୍ଧ କ୍ଷେତ୍ରଫଳ, କାର୍‌ଟି ଅତିକ୍ରାନ୍ତ କରୁଥିବା ମୋଟ ଦୂରତାକୁ ସୂଚାଏ । ଦୂରତା (s) = ABCDE କ୍ଷେତ୍ର ର କ୍ଷେତ୍ରଫଳ = ଆୟତକ୍ଷେତ୍ରର = ABCD ag
କ୍ଷେତ୍ରଫଳ + A ADE ର କ୍ଷେତ୍ରଫଳ
= AB × BC + \(\frac {1}{2}\) (AD × ED)

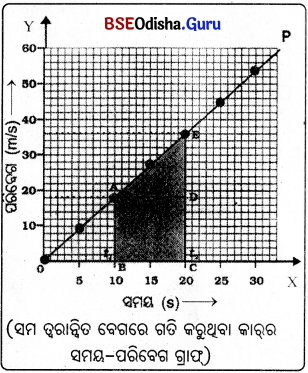
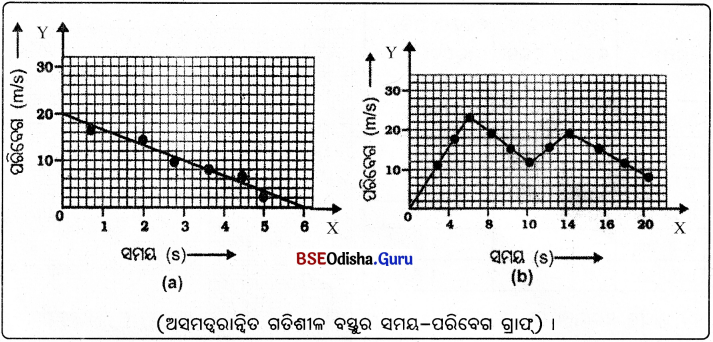
(c) ଅସମ ତ୍ଵରାନ୍ଵିତ ବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ :
(i) ଅସମ ତ୍ଵରାନ୍ଵିତ ବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ ପରିବେଗ ଗ୍ରାଫ୍ ଯେକୌଣସି ଆକୃତିର ହୋଇପାରେ ।
(ii) ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ (a)ରେ ବସ୍ତୁର ପରିବେଗ ସମୟ ଅନୁ ସାରେ ହ୍ରାସ ପାଇଛି ।
(iii) ଗ୍ରାଫ୍ (b)ରେ ବସ୍ତୁ ଅସମ ପରିବର୍ତ୍ତୀ ପରିବେଗରେ ଗତି କରୁଛି ।

→ ଲୈଖୁକ ପଦ୍ଧତିରେ ଗତି ସମୀକରଣଗୁଡ଼ିକର ବ୍ୟୁତ୍ପତ୍ତି (Derivation of Equations of Motion by Graphical Methods):
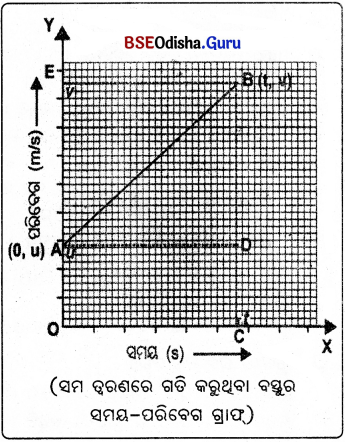
(i) ମନେକର ଗୋଟିଏ ବସ୍ତୁ ଏକ ସରଳରେଖାରେ ସମ ତ୍ଵରଣରେ ଗତି କରୁଛି । ବସ୍ତୁଟି ଗୋଟିଏ ବିନ୍ଦୁରୁ ବାହାରି । ସମୟ ପରେ ଆଉ ଗୋଟିଏ ସ୍ଥାନରେ ପହଞ୍ଚୁଛି । t = 0 ସମୟରେ ବସ୍ତୁର ପ୍ରାରମ୍ଭିକ ପରିବେଗ = u
t ସମୟରେ ବସ୍ତୁର ଅନ୍ତିମ ପରିବେଗ = v
ଗତି କରୁଥିବା ସମୟ ଅବଧୂ = t
ବସ୍ତୁର ତ୍ଵରଣ = a
t ସମୟ ପରେ ବସ୍ତୁଦ୍ଵାରା ଅତିକ୍ରାନ୍ତ ଦୂରତା = s
(ii) X-ଅକ୍ଷରେଖାରେ ସମୟକୁ ଏବଂ Y-ଅକ୍ଷରେଖାରେ ଗତି କରୁଥ‌ିବାରୁ ସମୟ-ପରି ବେଗ ଗ୍ରା, AB ସରଳରେଖାଦ୍ଵାରା ଦର୍ଶାଯାଇଛି ।
(iii) B ବିନ୍ଦୁରୁ X-ଅକ୍ଷରେଖା ପ୍ରତି BC ଲମ୍ବ ଅଙ୍କନ କରାଯାଉ ଯାହା À ବିନ୍ଦୁରୁ X-ଅକ୍ଷରେଖା ପ୍ରତି ଅଙ୍କିତ AD ସମାନ୍ତର ରେଖା BCକୁ D ବିନ୍ଦୁରେ ଛେଦ କରିବ ।

(iv) ଏହି ରାଶିମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କକୁ ତିନୋଟି ସମୀକରଣ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରିହେବ । ଏମାନଙ୍କୁ ଗତି ସମୀକରଣ (Equation of Motion) କୁହାଯାଏ । ଏହି ସମୀକରଣଗୁଡ଼ିକ ହେଲା –

→ ପ୍ରଥମ ଗତି ସମୀକରଣ
ସମୟ-ପରିବେଗ ସମ୍ପର୍କିତ ସମୀକରଣ (Equation for Velocity-Time Relation):
A ବିନ୍ଦୁ t = 0 ସମୟରେ ବସ୍ତୁର ପ୍ରାରମ୍ଭିକ ଅବସ୍ଥାନ ଏବଂ ଏହାର ନିର୍ଦ୍ଦେଶାଙ୍କଦ୍ଵୟ (0, u) । B ବିନ୍ଦୁ t = t ସମୟରେ ବସ୍ତୁର ଅନ୍ତିମ ଅବସ୍ଥାନ ଏବଂ ଏହାର ନିର୍ଦ୍ଦେଶାଙ୍କ ଦ୍ଵୟ (t, v) ।
OA = DC = u, BC = v, AD = t, BD = BC – DC = v – u

∴ v = u + at ଏହା ପ୍ରଥମ ଗତି ସମୀକରଣ ଅଟେ ।

ଦ୍ଵିତୀୟ ଗତି ସମୀକରଣ :
→ ସମୟ-ଅବସ୍ଥାନ ସମ୍ପର୍କ ସମୀକରଣ (Equation for Position-Time Relation):
(i) ଗୋଟିଏ ବସ୍ତୁର ବିସ୍ଥାପନ ଓ ସମୟ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କର ସମୀକରଣକୁ ଦ୍ୱିତୀୟ ଗତି ସମୀକରଣ କୁହାଯାଏ ।
(ii) ଦତ୍ତ ଚିତ୍ରରେ ଲେଖ AB ଏକ ସମ ତ୍ଵରାନ୍ଵିତ ବସ୍ତୁର ସରଳରେଖ୍ୟକ ଗତି ପାଇଁ ଅଙ୍କିତ ହୋଇଛି ।
(iii) ମନେକର ବସ୍ତୁଟି ମୂଳବିନ୍ଦୁରୁ ଯାତ୍ରା ଆରମ୍ଭ କରି ଏକ ସରଳରେଖାରେ ତ୍ଵରଣ ଥରେ ଗତିକରି । ସମୟ ମଧ୍ୟରେ s ଦୂରତା ଅତିକ୍ରମ କରିଛି ।
(iv) ଲେଖ AB ଓ X-ଅକ୍ଷରେଖା ମଧ୍ଯରେ t ସମୟ OABCର କ୍ଷେତ୍ର ଳ t ସମୟ ମଧ୍ୟରେ ବସ୍ତୁଦ୍ଵାରା ଅତିକ୍ରାନ୍ତ ଦୂରତା s ର ପରିମାଣ ସହ ସମାନ ।
s = OABC କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ
= OADC ଆୟକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ + ∆ ABDର କ୍ଷେତ୍ରଫଳ
= (OA × OC) + \(\frac {1}{2}\) (AD × BD) = u x t + \(\frac {1}{2}\) t × at (∵ BD = v – u = at) = ut + \(\frac {1}{2}\) at²
s = ut + \(\frac {1}{2}\) at² ଏହା ଦ୍ଵିତୀୟ ଗତି ସମୀକରଣ ଅଟେ।

ତୃତୀୟ ଗତି ସମୀକରଣ :
ପରିବେଗ-ଅବସ୍ଥାନ ସମ୍ପର୍କିତ ସମୀକରଣ (Equation for Position-Velocity Relation):
ବସ୍ତୁର ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍‌ରେ ବସ୍ତୁଟି t ସମୟ ମଧ୍ୟରେ ଅତିକ୍ରାନ୍ତ କରୁଥିବା ଦୂରତା sକୁ ଅନ୍ୟ ଏକ ସମୀକର ଦ୍ଵାରା ପ୍ରକାଶ କରାଯାଇପାରିବ

→ ସମବୃତ୍ତୀୟ ଗତି (Uniform Circular Motion):
(i) ବୃତ୍ତକାର ପଥରେ ଗୋଟିଏ ବସ୍ତୁ ସମବେଗରେ ଗତି କରିବାକୁ ସମବୃତ୍ତୀୟ ଗତି କୁହାଯାଏ ।
(ii) କୌଣସି ବସ୍ତୁର ପରିବେଗରେ ପରିବର୍ତ୍ତନ ହେଲେ ବସ୍ତୁଟି ତ୍ଵରାନ୍ଵିତ ଗତି କରୁଛି ବୋଲି କୁହାଯାଏ । ପରିବେଗରେ ପରିବର୍ତ୍ତନ ପରିବେଗର ପରିମାଣ କିମ୍ବା ଦିଗ କିମ୍ବା ଉଭୟର ପରିବର୍ତ୍ତନ ଯୋଗୁଁ ହୋଇଥାଏ ।
(iii) ବୃତ୍ତାକାର ପଥରେ ଗତି କରିବା ଏକ ତ୍ଵରାନ୍ଵିତ ଗତି ଅଟେ ।
(iv) ମନେକର ଗୋଟିଏ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r
∴ ବୃତ୍ତର ପରିଧ୍ଵ = 2πr
ଯଦି ଜଣେ ଧାବକ ଗୋଟିଏ ଥର ବୃତ୍ତାକାର ପଥରେ ଗତି କରିବାକୁ t ସେକେଣ୍ଡ ସମୟ ନିଏ, ଧାବକର ବେଗ