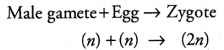Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 5 Heredity and Variation Important Questions and Answers.
CHSE Odisha 12th Class Biology Important Questions Chapter 5 Heredity and Variation
Heredity and Variation Class 12 Important Questions CHSE Odisha
Very Short Answer Type Questions
Choose the correct option
Question 1.
The process of physical removal of anthers is called …………
(a) emasculation
(b) mass selection
(c) introduction
(d) mutation
Answer:
(a) emasculation
Question 2.
Which term did Mendel use to denote something in germ cells responsible for transmission of characters?
(a) Chromosome
(b) Element
(c) Factor
(d) Gene
Answer:
(c) Factor
Question 3.
The character that is expressed in the F1 is called ……….
(a) recessive character
(b) dominant character
(c) codominant
(d) None of these
Answer:
(b) dominant character
Question 4.
An individual who has two different alleles of a gene is called ……………..
(a) allelopathic
(b) homozygous
(c) heterozygous
(d) codominant
Answer:
(c) heterogyzous
Question 5.
A cross of F1 with the recessive parent is known as
(a) back cross
(b) hybrid cross
(c) test cross
(d) double cross
Answer:
(c) test cross
Question 6.
The crose between F1 hybrid and the double recessive parent is called
(a) test cross
(b) double cross
(c) reciprocal cross
(d) complementary cross
Answer:
(c) test cross
Question 7.
If tallness (TT) is dominant and dwarfness (tt) is recessive, then a cross between ……….. will yield offspring of which 50% are dwarf.
(a) TT × tt
(b) Tt × tt
(c) tt × tt
(d) Tt × Tt
Answer:
(b) Tt × tt
Question 8.
The work of Mendel was published in 1866 before the Natural Science Society of Brunn in a paper named
(a) hybridisation on pea plant
(b) inheritance pattern in pea plant
(c) experiments in plant hybridisation
(d) Mendelian experiments on pea plant
Answer:
(c) experiments in plant hybridisation
Question 9.
The scientist not associated with the rediscovery of Mendel’s work is
(a) Hugo de Vries
(b) Carl Correns
(c) Erich von Tschermak
(d) William Bateson
Answer:
(d) William Bateson
Question 10.
Which one is not the reason for the success of Mendel?
(a) Made statistial analysis of the offsprings
(b) Kept accurate records
(c) Select pea plant
(d) Only did self-pollination in plants
Answer:
(d) Only did self-pollination in plants
Question 11.
Which one is a heterozygous condition?
(a) RR
(b) rr
(c) Rr
(d) RRrr
Answer:
(c) Rr
Question 12.
Phenotype is
(a) the genetic make up of an individual
(b) the same for parent and offspring
(c) the account of physiological activities
(d) the appearance of an individual
Answer:
(d) the appearance of an individual
Question 13.
To determine the heterozygosity of a cross, one has to perform
(a) back cross
(b) test cross
(c) reciprocal cross
(d) All of the above
Answer:
(b) test cross
Question 14.
The genetic ratio of 9 :3: 3:1 is due to
(a) segregation of characters
(b) crossing over of characters
(c) independent assortment of genes
(d) homologous pairing between chromosomes
Answer:
(c) independent assortment of genes
Question 15.
Organisms phenotypically similar but genotypically different are said to be
(a) heterozygous
(b) monozygous
(c) multizygous
(d) homozygous
Answer:
(a) heterozygous
Question 16.
Lack of independent assortment of two genes A and B in fruitfly is due to
(a) repulsion
(b) recombination
(c) linkage
(d) crossing over
Answer:
(c) linkage
Question 17.
The gene which controls many characters is called
(a) codominant gene
(b) polygene
(c) pleiotropic gene
(d) multiple gene
Answer:
(c) pleiotropic gene
Question 18.
A linkage group is explained as
(a) different groups of genes located on the same chromosome
(b) all the linked genes of a chromosome
(c) all genes of a chromosome
(d) None of the above
Answer:
(b) all the linked genes of a chromosome
Question 19.
Crossing over brings about
(a) recombination of genes
(b) no significant change
(c) sturdy offspring
(d) cytoplasmic reorganisation
Answer:
(a) recombination of genes
Question 20.
Different mutations referrable to the same locus of a chromosome gives rise to
(a) multiple alleles
(b) pseudoalleles
(c) polygenes
(d) oncogenes
Answer:
(a) multiple alleles
Question 21.
ABO blood group is an example of
(a) pseudoalleles
(b) isoalleles
(c) multiple alleles
(d) cytoplasmic inheritance
Answer:
(c) multiple alleles
Question 22.
Sutton gave chromosomal theory of inheritance, he united the knowledge of chromosomal segregation with
(a) recombination
(b) crossing over
(c) Both (a) and (b)
(d) Mendelian principle of segregation
Answer:
(d) Mendelian principle of segregation
Question 23.
The phenomenon of single gene contributing to multiple phenotypic traits is called
(a) pleiotropy
(b) codominance
(c) incomplete dominance
(d) polygenic inheritance
Answer:
(a) pleiotropy
Question 24.
Multiple alleles control the inheritance of in man.
(a) phenylketonuria
(b) colour blindness
(c) sickle-cell anaemia
(d) blood groups
Answer:
(d) blood groups
Question 25.
An incomplete dominance is shown by
(a) Pisum sativum
(b) Neurospora
(c) Mirabilis jalapa
(d) Lathyrus odoratus
Answer:
(c) Mirabilis jalapa
Question 26.
Pleiotropy occurs when a gene has
(a) a complementary gene elsewhere
(b) a small effect on one trait
(c) reversible effects on the phenotype, depending on age
(d) many effects on the phenotype
Answer:
(d) many effects on the phenotype
Question 27.
Crossing over occurs at
(a) 2 strand stage
(b) 4 strand stage
(c) Both (a) and (b)
(d) None of these
Answer:
(b) 4 strand stage
Question 28.
The number of linkage group found in Drosophila is
(a) 1
(b) 3
(c) 2
(d) 4
Answer:
(d) 4
Fill in the blanks
Question 1.
The basic unit of heredity is …………… .
Answer:
gene
Question 2.
An organism in which two alleles of a trait are unlike is called …………….. .
Answer:
heterozygous
Question 3.
An allele of T is …………
Answer:
t
Question 4.
Test cross is a cross between and ……….. .
Answer:
Tt, tt
Question 5.
A man with blood group ‘AB’ marries a woman with ‘O’ blood group. The blood group of offsprings will be ……………. .
Answer:
either ‘A’ or ‘B’ blood group
Question 6.
Phenylketonuria is an example of …………….. .
Answer:
pleiotropy
Question 7.
During incomplete dominance, phenotypic ratio is ………….. .
Answer:
1:2:1
Question 8.
Skin colour inheritance in humans is an example of …………..
Answer:
Polygenic inheritance
Correct the sentences, if required, by changing the underlined word(s)
Question 1.
Griffith coined the term ‘gene’ for Mendelian factor.
Answer:
Wilhelm Johannsen.
Question 2.
Inheritance is the degree by which progeny differs from their parents.
Answer:
Variation
Question 3.
Monohybrid cross yields two numbers of genotype.
Answer:
one
Question 4.
The genetic ratio in F2-generation of Mendel’s monohybrid cross is 9:3 : 3:1.
Answer:
1:2:1
Question 5.
A cross in which parents differ in a single pair of contrasting character is called dihybrid cross.
Answer:
monohybrid cross
Question 6.
Allelomorphs or alleles indicate identical characters of an individual.
Answer:
contrasting
Question 7.
The number of phenotypic classes is same as to the genotype in complete dominance.
Answer:
incomplete
Question 8.
In a cross between red and white flowered plants, F1-hybrids are pink. This is called quantitative dominance.
Answer:
incomplete
Question 9.
When two or more genes equally express themselves, they are called dominant genes.
Answer:
codominant
Question 10.
Inheritance of skin colour in man is monogenic.
Answer:
polygenic
Question 11.
Inheritance of skin colour in man is monogenic.
Answer:
polygenic
Question 12.
Multiple allelism is the phenomenon in which a single gene regulates several phenotypes.
Answer:
Pleiotropy
Express in one or two word(s)
Question 1.
These express contrasting characters of an individual.
Answer:
Alleles
Question 2.
Sum total of heredity or genetic makeup.
Answer:
Genome
Question 3.
Represent the genetic make up or gene complement of an organism.
Answer:
Genotype.
Question 4.
It is a simple square-shaped diagram which is drawn to show the possible combinations of male and female gametes of F1-parents.
Answer:
Punnett square.
Question 5.
Genes located in the same chromosome and being inherited together.
Answer:
Linked genes.
Question 6.
Skin colour inheritance in humans is an example of
Answer:
polygenic inheritance
Question 7.
In this phenomenon, the number of phenotypic classes is same as to the genotype.
Answer:
Incomplete dominance
Question 8.
In this phenomenon, both the genes of allelomorphic pair express themselves equally in the F1-hybrids.
Answer:
Codominance
Short Answer Type Questions
Question 1.
Mention the advantages of selecting pea plant for experiment by Mendel.
Answer:
Mendel’s Experimental Material
He selected garden pea plant as a sample due to the following reasons
- Pea plants are readily available on large scale and has bisexual cleistogamous flowers.
- Peas are self-pollinated and can be cross-pollinacd also.
- These are annual plants with short life cycle. So, several generations can be studied within a short period.
- Pea plants could be easily raised, maintained and handled.
- Pea plants differ in distinct/contrasting characteristics, which provide many easily detectable contrasting characters.
Question 2.
Write a note on emasculation.
Answer:
Mendel conducted artificial/cross-pollination experiments by performing emasculation (removal of anthers) on several true-breeding pea lines. A true-breeding line refers to one that have undergone continuous self-pollination and show stable trait inheritance and expression for several generations.
Mendel selected 14 true-breeding pea plant varieties as pairs, which were similar except for one character with contrasting traits.
Question 3.
Write short note with 2-3 important points on law of segregation.
Answer:
Principle of Segregation:
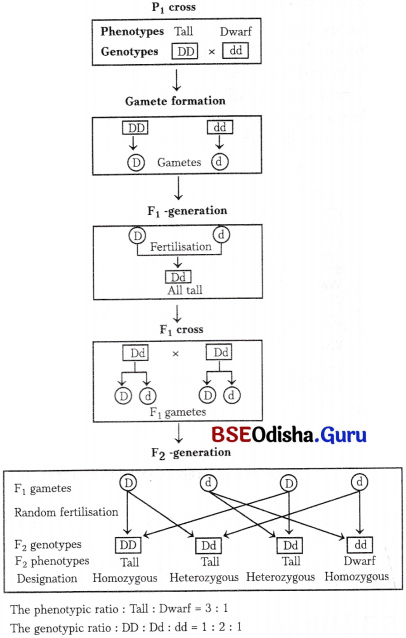
This principle states that, though the parents contain two alleles during gamete formation, the factors or alleles of a pair segregate from each other, such that a gamete receives only one of the two factors. Hence, the alleles do not show any blending and both the characters are recovered as such in the F2-generation though one of these is not seen in the F1 -generation.
Question 4.
A cross was carried out between two pea plants showing contrasting traits of height of the plants. The result of the cross showed 50% parental characters.
(i) Work out the cross with the help of a Punnett square.
(ii) Name the type of the cross carried out.
Answer:
Following inferences were made by Mendel based on his observations
- He proposed that some ‘factors’ passed down from parent to offsprings through the gametes over successive generations. Now-a-days, these factors are known as genes. Genes are hence, the units of inheritance. Genes which code for a pair of contrasting traits are known as alleles or allelomorphs, i.e. they are slightly different forms of the same gene.
- Genes occur in pairs in which, one dominates the other called as the dominant factor or the gene which expresses itself, while the other remains hidden and is called recessive factor.
- Allele can be similar in case of homozygous (TT or tt) and dissimilar in case of heterozygous (Tt).
- In a true-breeding tall or dwarf pea variety, the allelic pair of genes for height are identical or homozygous.
- TT and tt are called genotype (sum total of heredity or genetic make up) of the plant, while the term tall and dwarf are the phenotype.
- When tall and dwarf plants produce gametes by process of meiosis, the alleles of the parental pair segregate and only one of the alleles gets transmitted to a gamete. Thus, there is only 50% chance of a gamete containing either allele, as the segregation is a random process.
- During fertilisation, the two alleles, ‘T’ from one parent and V from other parent are united to produce a zygote, that has one ‘T’ and one ‘t’ allele or the hybrids have Tt.
- Since, these hybrids contain alleles which express contrasting traits, the plants are heterozygous.
Question 5.
Using a Punnett square, work out the
distribution of phenotypic features in the first (F1) filial generation after a cross between a homozygous female and a heterozygous male for a single locus.
Answer:
Homozygous female – WW
Hetrozygous – Ww
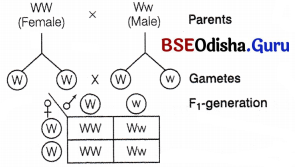
In this case, all F1 -generation is with dominant trait, i.e. 50% with homozygous and 50% with heterozygous nature.
Question 6.
When a cross is made between tall plant with yellow seeds (TtYy) and tall plant with green seeds (Ttyy), what proportions of phenotype in the offsprings could expected to be?
(i) Tall and green
(ii) Dwarf and green
Answer:
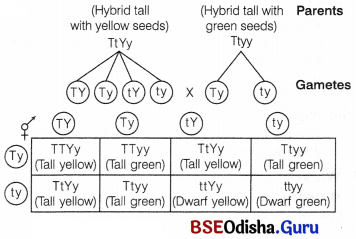
Tall green – 3/8 or 6/16
Dwarf green – 1/8 or 2/16
phenotypic ratio = 3 : 1
Question 7.
How are alleles of particular gene differ from each other? Explain its significance.
Answer:
Alleles are polymorphs that differ in their nucleotide sequence resulting in contrasting phenotypic expression. Alleles are the alternative forms of a same gene, e.g. genes for height have two alleles, one for dwarfness (t) and one for tallness (T). Significance of alleles are
(i) A character may have two or more contrasting phenotypic expressions, thus resulting in variation in a population.
(ii) These are used in the studies of inheritance and in understanding their behaviour.
Question 8.
During a monohybrid cross involving a tall pea plant with a dwarf pea plant, the offspring populations were tall and dwarf in equal ratio. Workout a cross to show how it is possible.
Answer:
In a monohybrid test cross, involving a heterozygous tall plant (Tt) and a pure dwarf plant, the progeny consists of tall and dwarf plants in the ratio of 1:1.
This can be shown as given below
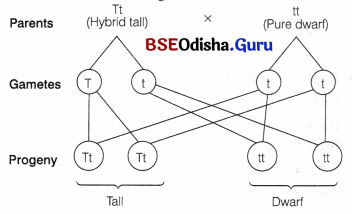
Question 9.
Write a short note on Mendel’s principle of dominance.
Answer:
Principle of Dominance:
It states that when two contrasting alleles for a character come together in an organism, only one is expressed completely and shows visible effect. This allele is called dominant and the other allele of the pair which does not express and remains hidden is called recessive.
For example, in the monohybrid cross when dwarf plant is crossed with tall plant, the Frgeneration are all tall plants. This shows that allele for tallness is dominant.
Question 10.
Define and design a test cross.
Answer:
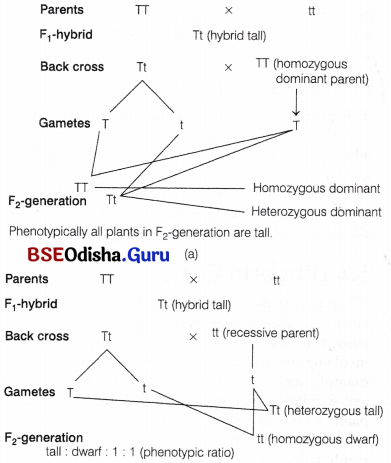
Back Cross and Test Cross
Back cross is a cross of F1 -progeny back to one of their parents. In back cross, there can be two possibilities, i.e. F1 -hybrid to be crossed with homozygous dominant parent or with homozygous recessive parent.
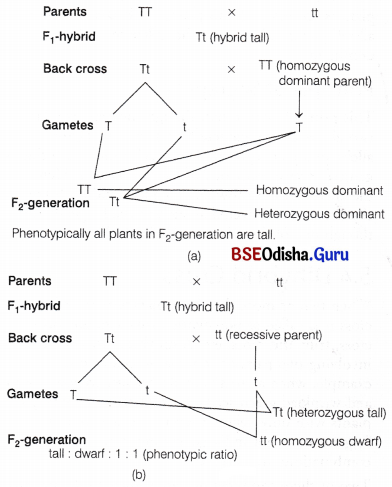
(a), (b): Diagrammatic representation of back cross
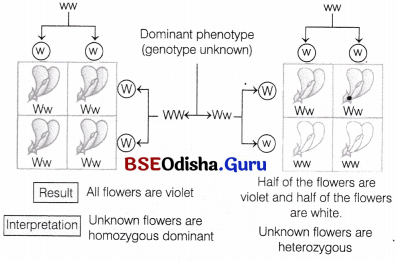
A special back cross to the recessive parent is known as test cross. This method was devised by Mendel to determine whether the dominant phenotype is homozygous or heterozygous.
For example, in a monohybrid cross between violet colour flower (W) and white colour flower (w), the F1-hybrid was a violet colour flower. If all the F1-progenies are of violet colour, then the dominant flower is homozygous and if the progenies are in 1:1 ratio, then the dominant flower is heterozygous.
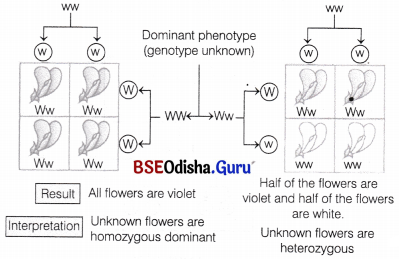
Diagrammatic representation of a test cross
Question 11.
A teacher wants his/her students to find the genotype of pea plants bearing purple coloured flowers in their school garden. Name and explain the cross that will make it possible.
Answer:
Test cross is a method devised by Mendel to determine the genotype of plant with dominant phenotype (purple flower in this case).
In a test cross, the unknown dominant genotype is crossed with recessive parent (white, WW in the given case).
(i) If the progeny consists of purple and white flowers in ratio of 1 : 1, the purple flower is a hybrid with – PW genotype. It can be seen from the given cross.
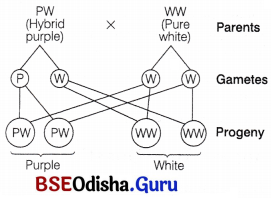
(ii) If the progeny obtained have all purple flowers, both parents are homozygous, i.e. genotype of purple flower; is PP. It can be seen from the cross that follows
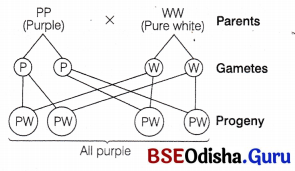
Question 12.
When tall pea plants were selfed, some of the offsprings were dwarf. Explain with the help of a Punnett square.
Answer:
Punnett Square
The production of gametes by the parents, the formation of zygotes, the F1 and F2-generations can be explained by a diagram called Punnett square. It was developed by British geneticist Reginald C Punnett.
It is a graphical representation to calculate the probability of all possible genotypes of offsprings in a genetic cross, as shown in the figure (5.2).
The 1/4 : 1/2 : 1/4 ratio of TT : Tt : tt is mathematically condensable in the form of the binomial expression (ax+ by)2, that has the gametes bearing genes T or t in equal frequency of 1/2. The expression is expanded as
(1/2T + 1/2t)2 = (1/2T + 1/2t) x (1/2T + 1/2t)
= \(\frac{1}{4}\) TT + 1/2T t + 1/4tt
Though the genotypic ratios can be calculated using mathematical probability, but it is not possible to know the genotypic composition by looking at the phenotype of a dominant trait.
Therefore, to solve this problem Mendel devised test cross.
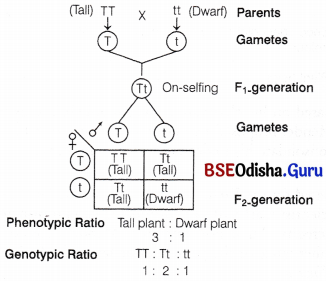
A Punnett square used to understand a typical monohybrid cross conducted by Mendel between true breeding tall plant and true-breeding dwarf plant
Question 13.
A pea plant with purple flowers was crossed with white flowers producing 50 plants with only purple flowers. On selfing, these plants produced 482 plants with purple flowers and 162 with white flowers. What genetic mechanism accounts for these results? Explain.
Answer:
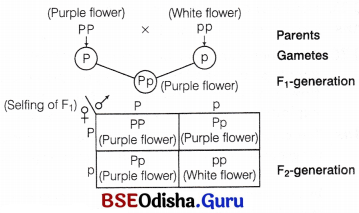
Phenotypic ratio is
Purple flowered plants : White flowered plants
3(482) : 1(162)
Mechanism is as follows
(i) Factors segregate from each other that remained together in a hybrid during gamete formation.
(ii) A homozygous parent produces all gametes that are similar while heterozygous parent produces two kinds of gametes in equal ratio.
Question 14.
Write a short note on law of independent assortment.
Answer:
Law of Independent Assortment
It states that when two pairs of traits are combined in a hybrid, segregation of one pair of traits is independent to the other pair of traits. As in the dihybrid cross of Mendel the presence of new combinations, i.e. round-green and wrinkled-yellow suggests that the genes for shape of seed and colour of seed are assorted independently. The results (9:3:3:1), indicate that yellow and green seeds appear in the ratio of 9+3 : 3+1 = 3:1. Similarly, the round and wrinkled seeds appear in the ratio of 9+3 : 3+1 = 3:1.
This indicates that each of the two pairs of alternative characters viz yellow-green cotyledon colour is inherited independent of the round-wrinkled characters of the cotyledons. It means that at the time of gamete formation the factor for yellow colour enters the gametes independent of R or r, i.e. gene Y can be passed on to the gametes either with gene R or r.
Question 15.
With the help of one example, explain the phenomenon of codominance and multiple allelism in human population.
Answer:
Codominance
It is the phenomenon in which two alleles express themselves independently when present together in an organism. In other words, it is the phenomenon in which offspring shows resemblance to both the parents, e.g.
ABO blood grouping in humans.
ABO blood groups are controlled by the gene-I.
The plasma membrane of the red blood cells has sugar polymers that protrude from its surface and the kind of sugar is controlled by the gene. The gene I has three alleles IA, IB and i. The alleles IA and IB produce a slightly different form of the sugar while, allele i does not produce any sugar. In humans, each person possesses any two of the three I gene alleles. IA and IB are completely dominant over i. When IB and i are present, only IB expresses (because i does not have any sugar), same is the case with IA and i.
But when IA and IB are present together, they both express their own types of sugars, this is due to codominance. Therefore, the red blood cells have both A and B-types of sugars. Since, there are three different types of alleles, there can be six different combinations. More information about blood type is discussed under multiple alleles.
In case of plants, when a red and white flowered plants are crossed, the progeny bears flowers that have red and white spots. When these plants are self-pollinated,
F2-generation will have genotypic ratio of 1 : 2 : 1 (Red : Spotted : White).
Multiple Allelism and Inheritance of Blood Groups:
Each gene has alternative forms or allelomorphs. For example, the genes for tall and dwarf characters of pea plant are alleles or allelomorphs. Here, former is called normal or wild type and later as mutant type. Sometimes, there may not be any alternative form such mutation that results in complete elimination of a gene is known as null mutation. Sometimes silent mutation occurs in which mutation does not have any effect of all.
These mutations occur in wild gene in any direction with a possibility of formation of many alternative alleles. Some genes may occur in more than two allelic forms, i.e. a gene can mutate several times to produce several alternative expressions such genes are called multiple alleles.
The multiple alleles can be defined as set of 3, 4 or more allelomorphic genes or allele, which have arises as a result of mutation of the normal gene and which occupy the same locus in the homologous chromosomes.
A mutant gene series is said to be multiple alleles only if they possess following characteristics
(i) Occupy same locus in homologous chromosome pair.
(ii) Since, only rwo chromosomes (homologous pair) of each type present in each diploid cell hence, only two alleles of a gene are found in a cell or in a given individual.
(iii) Gametes normally contain only one chromosome out of the pair. Hence, only one allele of a gene is found in one gamete.
(iv) Due to their presence on same locus, they do not exhibit the phenomenon of crossing over in themselves.
(v) They always regulate same characteristic, but with a variable degree of efficiency.
(vi) Within a multiple series, a wild type is always dominant over normal genes and others may be dominant or intermediate.
Question 16.
How does the gene T control ABO blood groups in humans? Write the effect the gene has on the structure of red blood cells.
Answer:
ABO Blood Group
ABO blood group in humans serves as a very good example of multiple alleles. It shows the phenomenon of both complete dominance and codominance. In humans, group-A, B, AB and O types of blood groups are discovered. A set of three multiple alleles on the chromosome-9 is responsible for the four blood types.
These different types of blood groups are due to the occurrence of different types of antigens present on the surface of RBC. The genes which are responsible for the production of these antigens is being called as I. This gene is present in the form of three alleles which are IA, IB and VI i. IA codes for enzyme that adds galactosamine on the surface of RBC. So, blood group-A individuals have only galactosamine added on the cell surface of RBC.
IB codes for the enzyme that add galactose on the surface of RBC and so blood group-B individuals have only galactose added to the cell surface of RBC.
Individuals belonging to AB blood group possess both the sugars added on the surface of RBC and individuals with blood group-O do not have any sugar added on the surface of RBC. People homozygous for the recessive i allele belong to blood group-O.
The Relationship Between ABO Genotype and Blood type (group)

Both IA and IB are dominant to i. Thus, you will express blood group-A, if you are either IA/Aor IAi and you will express blood group-B, if you are either IB / IB or IB/i. Heterozygous IA/IB individuals express blood group-AB.
Question 17.
Briefly mention the contribution of TH Morgan in genetics.
Answer:
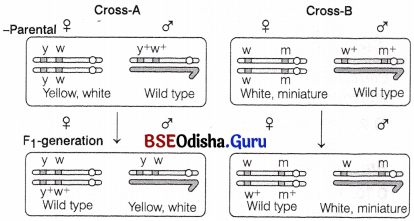
Morgan and his group also found that even when genes were grouped on the same chromosome, some genes were tightly linked, i.e. linkage is stronger between two genes, if the frequency of recombination is low (cross-A). Whereas, the frequency of recombination is higher, if genes are loosely linked, i.e. linkage is weak between two genes (cross-B) as given in below.
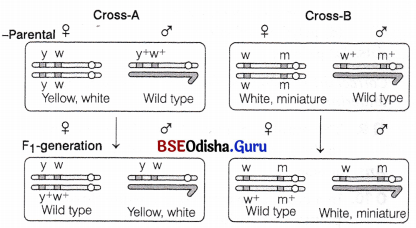
Linkage : Results of two dihybrid crosses conducted by Morgan. Cross ‘A’ shows crossing between genes y and w ; Cross ‘B’ shows crossing between genes w and m. Here, dominant wild type alleles are represented with ( + ) sign in superscript
Those traits present on same chromosome, which do not show any production of recombinants are completely linked which is known as complete linkage and it is very rare.
Question 18.
Linkage and crossing over of genes are alternatives of each other. Justify with the help of an example.
Answer:
Linkage is the tendency of certain loci or alleles (genes) to be inherited together while, crossing over is the segregation of genes, e.g. the genes on a chromosome either follow linkage path or cross over, to form the gametes during gametogenesis in human.
Question 19.
Two heterozygous parents are crossed. If the two loci are linked, what would be the distribution of phenotypic features in F1-generation for a dihybrid cross?
Answer:
If the two loci in parents are completely linked, there would be no segregation. The F1-generation will exhibit parental characters only. But, if the two loci are incompletely linked, then segregation would occur partly and the F1-generation will exhibit both parental and recombinant characteristics, but the recombinants will be in a very small proportion.
Question 20.
Explain two situations, when independent assortment of genes occurs, resulting in 50% recombinants.
Answer:
Two situations are
(i) When the genes of different traits are located on the same chromosome and must be distantly located to enhance the recombination frequency.
(ii) When the genes of different traits may be located on different chromosomes.
Question 21.
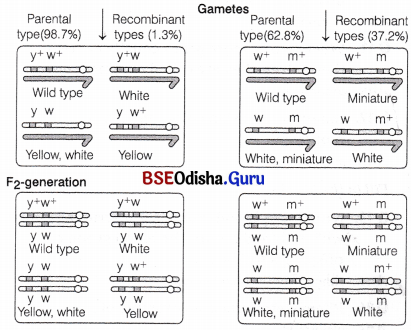
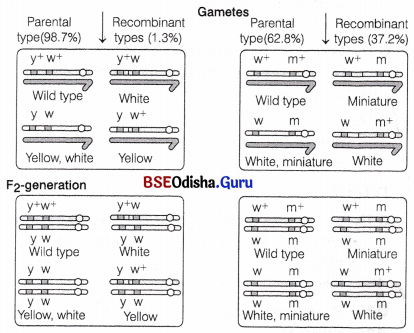
In a dihybrid cross, white-eyed, yellow-bodied female Drosophila was crossed with red-eyed, brown-bodied male Drosophila, produced in F2-generation are 1.3% recombinants and 98.7% progeny with parental type combinations. This observation of Morgan deviated from Mendelian F1-phenotypic .dihybrid ratio. Explain giving reasons, Morgan’s observations.
Answer:
Morgan saw that when the two genes in dihybrid cross were situated on same chromosome, the proportion of parental gene combinations were higher than non-parental type.
This is due to physical association of genes on a chromosome or linkage. In Morgan’s experiment, the genes for eye and body colour show linkage and do not always allow crossing to over during gamete formation. Hence, parental type progeny is in greater ratio than that of recombinants.
Question 22.
How do biologists use cross over frequencies to map genes on chromosomes?
Answer:
The farther the genes are on a chromosome, the more frequently they will cross over. By comparison, genes that are close together on a chromosome, are less likely to be separated. The analysis of how often the traits appear together, helps to establish linkage map, which shows the relative positions of genes on chromosomes.
Question 23.
(i) Explain the phenomenon of multiple allelism and codominance taking ABO blood group system as an example.
(ii) What is the phenotype of the following
(a) IAi (b) ii
Answer:
(i)
These mutations occur in wild gene in any direction with a possibility of formation of many alternative alleles. Some genes may occur in more than two allelic forms, i.e. a gene can mutate several times to produce several alternative expressions such genes are called multiple alleles.
It is the phenomenon in which two alleles express themselves independently when present together in an organism. In other words, it is the phenomenon in which offspring shows resemblance to both the parents, e.g.
ABO blood grouping in humans.
ABO blood groups are controlled by the gene-I.
The plasma membrane of the red blood cells has sugar polymers that protrude from its surface and the kind of sugar is controlled by the gene. The gene I has three alleles IA, IB and i. The alleles IAand IB produce a slightly different form of the sugar while, allele i does not produce any sugar. In humans, each person possesses any two of the three I gene alleles. IA and IB are completely dominant over i. When IB and i are present, only IB expresses (because i does not have any sugar), same is the case with IA and i.
But when IA and IB are present together, they both express their own types of sugars, this is due to codominance. Therefore, the red blood cells have both A and B-types of sugars. Since, there are three different types of alleles, there can be six different combinations. More information about blood type is discussed under multiple alleles.
(ii) (a) IAi – ‘A’ blood group
(b) ii – ‘O’ blood group
Question 24.
A child has blood group ‘O’. If the father has blood group ‘A’ and mother’s blood group is B, workout the genotypes of the parents and the possible genotypes of the other offsprings. .
Answer:
The child with blood group ‘O’ will have homozygous recessive alleles. Therefore, both the parents should be heterozygous, i.e. the genotype of father will be IAi afid the mother will be IBi.
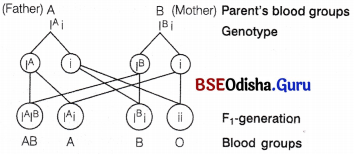
The other possible genotypes of offsprings will be ‘A’, ‘B’ and ‘AB’ blood groups.
Question 25.
Explain the following
(i) What is the most common example of pleiotropy in humans?
(ii) How are the pleiotropic genes useful?
Answer:
(i) In humans, the phenylketonuria, a disorder caused by mutation in the gene coding the enzyme phenylalanine hydroxylase serves as the best example. In this disorder, phenylalanine hydroxylase enzyme is deficient and is needed to convert essential amino acid phenylalanine to tyrosine.
Thus, tyrosine is not present which is being required for normal functioning of the body. Phenylalanine gets converted to phenylpyruvate which also creates problems. Tyrosine is required for protein biosynthesis and also as a precursor for neurotransmitters like norepinephrine, for pigment melanin and for hormone thyroxine. Thus, it leads to hair and skin pigmentation and mental retardation.
(ii) The pleiotropic genes provide us valuable information regarding the evolution of different genes and gene families. The pleiotropy reflects the fact that most proteins have multiple roles in distinct cell types.
Thus, any genetic change that alters gene expression or function can potentially have wide ranging effects in a variety of tissues.
Question 26.
State the significance of crossing over.
Answer:
The significance of crossing over are as follows
(i) Crossing over produced recombinations or new gene combinations which form variations which are the raw material in the formation of new species and evolution.
(ii) Useful recombination produced by crossing over are used in producing new varieties of plants and animals in breeding programme.
(iii) It is used for preparing linkage maps or determining location of genes in chromosomes.
Question 27.
What is chiasma?
Answer:
Crossing over takes place in the pachytene stage of meiosis-I, where there is exchange of segments between two non-sister chromatids. It occurs at several points all along their length and the point of contact between these non-sister chromatids of homologous chromosomes is called chiasma.
Question 28.
What is linkage? Mention its significance.
Answer:
The physical association of two genes on a chromosome is called linkage. It is the tendency of genes on a chromosome to remain together and is passed as such in the next generation. It is significant as it brings more parental gene combination types.
Question 29.
Write a short note on crossing over.
Answer:
Crossing over is the combination of genes due to the exchange of genetic material resulting from interchange of corresponding segments or parts of homologous chromosomes. This takes place in the pachytene stage of meiosis-I. It brings out new combination or recombination of genes.
Question 30.
Define multiple allelism.
Answer:
More than two alternative forms (allele) of a gene occupying the same locus on a chromosome in a population are known as multiple alleles. The ABO blood grouping is a good example of multiple alleles. In this case, more than two, i.e. three alleles are present governing the same character. Multiple alleles can be found only when population studies are made.
Question 31.
During his studies on genes in Drosophila that were sex-linked, TH Morgan found F2-population phenotypic ratio to be deviated from expected 9: 3: 3:1. Explain the conclusion he arrived at.
Answer:
Conclusion of Morgans experiments are
(i) Genes were located on the X-chromosome.
(ii) When the two genes in a dihybrid cross were studied on the same chromosome, the proportion of parental gene combinations were much higher than the non-parental type. Morgan stated this association as ‘linkage’ to describe the physical association of genes on a chromosome.
(iii) Morgan and his group also found that even when genes were grouped on the same chromosome, some genes were tightly linked (low recombination) and others were loosely linked (high recombination).
Question 32.
A woman with blood group ‘A’ marries a man with blood group ‘O’. Discuss the possibilities of the inheritance of the blood group in the following starting with ‘Yes’ or ‘No’ for each.
(a) They produce children with blood group ‘A’ only.
(b) They produce children some with ‘O’ blood group and some with ‘A’ blood group.
Answer:
(a) No, it is not necessary as mother could have a genotype IAIA or IAi. If the genotype is IA, all the offsprings would have ‘A’ blood group, but in the second case, offsprings can have either ‘A’ or ‘O’ blood group as their father has ‘O’ blood group.
(b) Yes, if the mother is A (genotype IAi) and father has ‘O’ (genotype ii) blood group, then the blood group of some children can be ‘O’ and some can be with blood group ‘A’.
Question 33.
Persons of which blood group are universal recipient?
Answer:
ABO blood group in humans serves as a very good example of multiple alleles. It shows the phenomenon of both complete dominance and codominance. In humans, group-A, B, AB and O types of blood groups are discovered. A set of three multiple alleles on the chromosome-9 is responsible for the four blood types.
These different types of blood groups are due to the occurrence of different types of antigens present on the surface of RBC. The genes which are responsible for the production of these antigens is being called as I. This gene is present in the form of three alleles which are IA, IB and I0/i. IA codes for enzyme that adds galactosamine on the surface of RBC. So, blood group-A individuals have only galactosamine added on the cell surface of RBC.
Question 34.
Explain ‘ABO blood group’.
Answer:
ABO blood group in humans serves as a very good example of multiple alleles. It shows the phenomenon of both complete dominance and codominance. In humans, group-A, B, AB and O types of blood groups are discovered. A set of three multiple alleles on the chromosome-9 is responsible for the four blood types.
These different types of blood groups are due to the occurrence of different types of antigens present on the surface of RBC. The genes which are responsible for the production of these antigens is being called as I. This gene is present in the form of three alleles which are IA, IB and I0 / i. IA codes for enzyme that adds galactosamine on the surface of RBC. So, blood group-A individuals have only galactosamine added on the cell surface of RBC.
IB codes for the enzyme that add galactose on the surface of RBC and so blood group-B individuals have only galactose added to the cell surface of RBC.
Individuals belonging to AB blood group possess both the sugars added on the surface of RBC and individuals with blood group-O do not have any sugar added on the surface of RBC. People homozygous for the recessive i allele belong to blood group-O.
Question 35.
Inheritance pattern of flower colour in garden pea plant and snapdragon differs. Why is this difference observed? Explain showing the crosses upto F2-generation.
Answer:
(i) Inheritance pattern of flower colour in garden pea plant
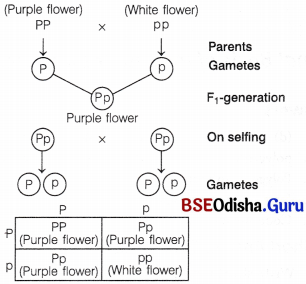
Phenotypic Ratio Purple : White
3 : 1
Genotypic Ratio PP : Pp : pp
1 : 2 : 1
Inheritance of flower colour in garden pea shows true dominance. In F1 -generation, dominant colour purple is expressed and in F2-generation both dominant (purple) and recessive (white) colour are expressed in the ratio of 3:1.
(ii) Inheritance pattern of flower colour in snapdragon is given below
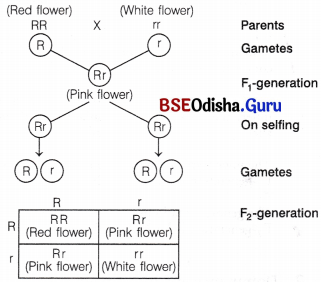
Phenotypic Ratio Red : Pink : White
1 : 2 : 1
Genotypic Ratio RR : Rr : rr
1 : 2 : 1
Inheritance in snapdragon flower colour shows incomplete dominance. In this phenomenon, neither of the two alleles are completely dominant over the other and the hybrid is-intermediate between the two. Hence, red is a homozygous dominant, white is a homozygous recessive, while hybrid is an intermediate, i.e. pink.
Question 36.
Explain the genetic basis of blood grouping in human population.
Answer:
‘ABO’ blood grouping in human shows the phenomenon of codominance (alleles are able to express themselves independently when present together) and multiple allelism (more than two alleles govern the same character).
ABO blood group in humans serves as a very good example of multiple alleles. It shows the phenomenon of both complete dominance and codominance. In humans, group-A, B, AB and O types of blood groups are discovered. A set of three multiple alleles on the chromosome-9 is responsible for the four blood types.
These different types of blood groups are due to the occurrence of different types of antigens present on the surface of RBC. The genes which are responsible for the production of these antigens is being called as I. This gene is present in the form of three alleles which are IA, IB and I0 / i. IA codes for enzyme that adds galactosamine on the surface of RBC. So, blood group-A individuals have only galactosamine added on the cell surface of RBC.
IB codes for the enzyme that add galactose on the surface of RBC and so blood group-B individuals have only galactose added to the cell surface of RBC.
Individuals belonging to AB blood group possess both the sugars added on the surface of RBC and individuals with blood group-O do not have any sugar added on the surface of RBC. People homozygous for the recessive i allele belong to blood group-O.
Question 37.
Can a child have blood group ‘O’ if his/her parents have blood group ‘A’ and ‘B’? Explain.
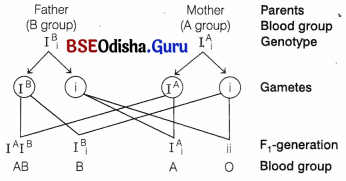
Answer:
The child with blood group ‘O’ will have homozygous recessive alleles. Therefore, both the parents should be heterozygous, i.e. genotype of father will be IA i or IB i and of mother will be IA i or IB i. A child have blood group ‘O’ in the following two cases
Case I When father is IA i and mother is IB
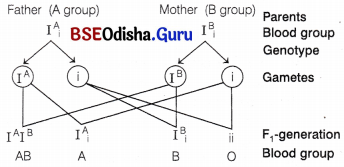
The offsprings will have the above possible blood groups, i.e. AB, A, B and O.
Case II When father is IB i and mother is IA i.
Question 38.
How do genes and chromosomes share similarity from the point of view of genetical studies?
Answer:
By 1902, the chromosome movement during meiosis had been worked out. Walter Sutton and Theodore Boveri (1902) noted that the behaviour of chromosomes was parallel to the behaviour of genes and used chromosome movement to explain Mendel’s laws. They studied the behaviour of chromosomes during mitosis (equational division) and during meiosis (reduction division). The chromosomes as well as genes occur in pairs and the two alleles of a gene pair are located on homologous sites of homologous chromosomes.
Chromosomes segregate when germ cells are formed.
Long Answer Type Questions
Question 1.
(i) Explain monohybrid cross taking seed coat colour as a trait in Pisum sativum. Workout the cross upto F2-generation.
(ii) State the laws of inheritance that can be derived from such a cross.
(iii) How is the phenotypic ratio of F2-generation different in a dihybrid cross?
Answer:
(i) In a monohybrid cross, when homozygous dominant and homozygous recessive parents are crossed, F1 -hybrid would be heterozygous for the trait and would express the dominant allele.
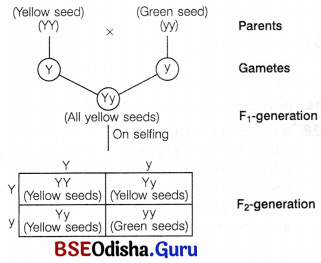
(ii) The hybrid is heterozygous containing both alternative alleles (Y and y) but only one trait,
i.e. yellow colour appeared and green colour trait is suppressed in F1 -generation. This shows that yellow seed colour is dominant over the green seed colour trait. This explains Mendel’s law of dominance.
(iii) Phenotypic ratio in F2-generation, Yellow seeds : Green seeds (3 : 1) in monohybrid cross and in dihybrid cross 9 : 3 : 3 : 1.
Question 2.
Workout a typical Mendelian dihybrid cross and state the law that he derived from it.
Answer:
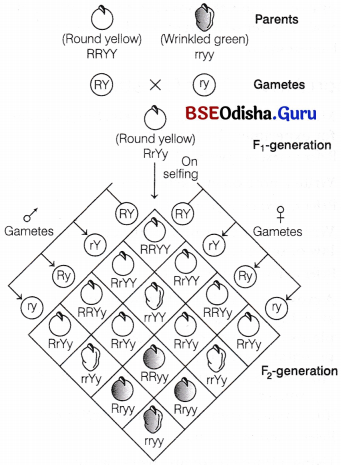
Dihybrid Cross:
When two or more than two characters are taken in a cross it is called as polyhybrid cross, e.g. dihybrid cross, trihybrid cross, etc. A dihybrid cross is a cross involving two pairs of contrasting characters. For example, when a cross is made between yellow-round and wrinkled green seeds (both pureline homozygous), plants with only yellow round seeds are seen in F1-generation but in F2-generation, four types of combinations are observed.
Two of these combinations are similar to the parental combinations and others are new combinations. These are round green and wrinkled yellow.
The cross can be seen as shown in the figure
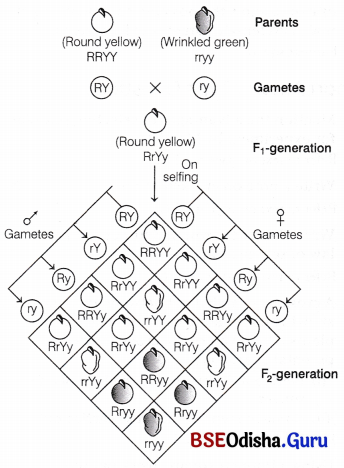
Phenotypic Ratio
Round yellow : Round green : Wrinkled yellow : Wrinkled green = 9 : 3 : 3 : 1
Genotypic Ratio 1 :2:2:4:1 :2:1 :2:1
Dihybrid cross between the two parents differed in two pairs of contrasting traits, i.e. seed colour and seed shape
The ratio of four combinations in F2-generation comes out to be 9 (round, yellow) : 3 (round, green) : 3 (wrinkled, yellow) : 1 (wrinkled, green). This ratio is called phenotypic dihybrid ratio. Phenotypic ratio of dihybrid test cross is 1 : 1 : 1 : 1.
Mendel’s Postulate Based on Dihybrid Cross:
Based on the result obtained from dihybrid crosses or two gene interaction, Mendel proposed the fourth postulate, i.e. law of independent assortment.
Question 3.
You are given tall pea plants with yellow seeds, whose genotypes are unknown. How would you find the genotype of these plants? Explain with the help of cross.
Answer:
The given tall pea plant with yellow seeds need to be crossed with a dwarf plant with green seeds.
(i) The dominant traits are tallness and yellow colour of seeds. The recessive traits are dwarfness and green colour of seeds.
(ii) Cross between tall plant/yellow seeds and dwarf plant/green seeds.
Cross showing heterozygous nature for both traits.
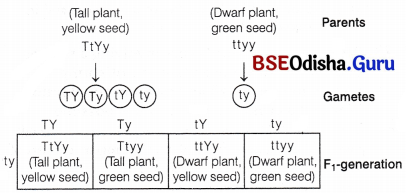
In this cross, the F1 -generation shows four phenotypes in the ratio of 1 : 1 : 1 : 1. So, the given plant is heterozygous for both the traits.
Question 4.
Explain Mendel’s dihybrid cross with a checker board.
Or Describe Mendel’s dihybrid cross with checker board.
Answer:
Dihybrid Cross:
When two or more than two characters are taken in a cross it is called as polyhybrid cross, e.g. dihybrid cross, trihybrid cross, etc. A dihybrid cross is a cross involving two pairs of contrasting characters. For example, when a cross is made between yellow-round and wrinkled green seeds (both pureline homozygous), plants with only yellow round seeds are seen in F1-generation but in F2-generation, four types of combinations are observed.
Two of these combinations are similar to the parental combinations and others are new combinations. These are round green and wrinkled yellow.
The cross can be seen as shown in the figure

Phenotypic Ratio
Round yellow : Round green : Wrinkled yellow : Wrinkled green = 9 : 3 : 3 : 1
Genotypic Ratio 1 :2:2:4:1 :2:1 :2:1
Dihybrid cross between the two parents differed in two pairs of contrasting traits, i.e. seed colour and seed shape
The ratio of four combinations in F2-generation comes out to be 9 (round, yellow) : 3 (round, green) : 3 (wrinkled, yellow) : 1 (wrinkled, green). This ratio is called phenotypic dihybrid ratio. Phenotypic ratio of dihybrid test cross is 1 : 1 : 1 : 1.
Mendel’s Postulate Based on Dihybrid Cross:
Based on the result obtained from dihybrid crosses or two gene interaction, Mendel proposed the fourth postulate, i.e. law of independent assortment.
Question 5.
Give an account of Mendel’s law of inheritance.
Or State and explain Mendel’s low of dominance.
Answer:
Dihybrid Cross:
When two or more than two characters are taken in a cross it is called as polyhybrid cross, e.g. dihybrid cross, trihybrid cross, etc. A dihybrid cross is a cross involving two pairs of contrasting characters. For example, when a cross is made between yellow-round and wrinkled green seeds (both pureline homozygous), plants with only yellow round seeds are seen in F1-generation but in F2-generation, four types of combinations are observed.
Two of these combinations are similar to the parental combinations and others are new combinations. These are round green and wrinkled yellow.
The cross can be seen as shown in the figure

Phenotypic Ratio
Round yellow : Round green : Wrinkled yellow : Wrinkled green = 9 : 3 : 3 : 1
Genotypic Ratio 1 :2:2:4:1 :2:1 :2:1
Dihybrid cross between the two parents differed in two pairs of contrasting traits, i.e. seed colour and seed shape
The ratio of four combinations in F2-generation comes out to be 9 (round, yellow) : 3 (round, green) : 3 (wrinkled, yellow) : 1 (wrinkled, green). This ratio is called phenotypic dihybrid ratio. Phenotypic ratio of dihybrid test cross is 1 : 1 : 1 : 1.
Mendel’s Postulate Based on Dihybrid Cross:
Based on the result obtained from dihybrid crosses or two gene interaction, Mendel proposed the fourth postulate, i.e. law of independent assortment.
Law of Independent Assortment:
It states that when two pairs of traits are combined in a hybrid, segregation of one pair of traits is independent to the other pair of traits. As in the dihybrid cross of Mendel the presence of new combinations, i.e. round-green and wrinkled-yellow suggests that the genes for shape of seed and colour of seed are assorted independently. The results (9:3:3:1), indicate that yellow and green seeds appear in the ratio of 9+3 : 3+1 = 3:1. Similarly, the round and wrinkled seeds appear in the ratio of 9+3 : 3+1 = 3:1.
This indicates that each of the two pairs of alternative characters viz yellow-green cotyledon colour is inherited independent of the round-wrinkled characters of the cotyledons. It means that at the time of gamete formation the factor for yellow colour enters the gametes independent of R or r, i.e. gene Y can be passed on to the gametes either with gene R or r.