Odisha State Board CHSE Odisha Class 11 Economics Solutions Chapter 20 ବିଚ୍ଛୁରଣର ପରିମାପ Questions and Answers.
CHSE Odisha 11th Class Economics Solutions Chapter 20 ବିଚ୍ଛୁରଣର ପରିମାପ
ବସ୍ତୁନିଷ୍ଠ ଓ ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନରେ ପ୍ରଦତ୍ତ ବିକଳ୍ପଉତ୍ତରମାନଙ୍କ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ।
୧। ଯେଉଁ ବିଜୁରଣ ପରିମାପ କ୍ଷୁଦ୍ରତମ ଓ ବୃହତ୍ତମ ଲବ୍ଧଙ୍କକୁ ବିଚାରକୁ ନେଇଥାଏ, ତାହା
(i) ମାଧ୍ୟ ବିଚ୍ୟୁତି
(ii) ମାନକ ବିଚ୍ୟୁତି
(iii) ବିସ୍ତାର
(iv) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(iii) ବିସ୍ତାର
୨। ୫୮, ୩୭, ୫୭, ୭୩ ଓ ୭୭ର ବିସ୍ତାର
(i) ୨୦
(ii) ୪୦
(iii) ୩୧
(iv) ୩୫
Answer:
(ii) ୪୦
୩। କେଉଁ ବିଚ୍ଛୁରଣ ପରିମାପ ରାଶିମାନଙ୍କର ୫୦% ପର୍ଯ୍ୟବେକ୍ଷଣକୁ ବିଚାରକୁ ନିଏ ?
(i) ମାଧ୍ୟ ବିଚ୍ୟୁତି
(ii) ମାଳକ ବିଚ୍ୟୁତି
(iii) ବିସ୍ତାର
(iv) ଚତୁର୍ଥାଶଂକ ବିଚ୍ୟୁତି
Answer:
(iv) ଚତୁର୍ଥାଶଂକ ବିଚ୍ୟୁତି
୪। କେଉଁ ବିଜୁରଣ ପରିମାପ ବିଜଗାଣିତିକ ନିୟମ ଲଙ୍ଘନ କରେ ?
(i) ମାଧ୍ୟ ବିଚ୍ୟୁତି
(ii) ମାନକ ବିଚ୍ୟୁତି
(iii) ବିସ୍ତାର
(iv) ଚତୁର୍ଥାଶଂକ ବିଚ୍ୟୁତି
Answer:
(i) ମାଧ୍ୟ ବିଚ୍ୟୁତି
୫। କେଉଁ ବିଚ୍ଛୁରଣ ପରିମାପ ମାଧ୍ଯମାନ କିମ୍ବା ମଧ୍ୟମାର ପରମବିଚ୍ୟୁତି ବବିଚାରକୁ ନେଇଥାଏ ?
(i) ମାଧ୍ୟ ବିଚ୍ୟୁତି
(ii) ମାନକ ବିଚ୍ୟୁତି
(iii) ବିସ୍ତାର
(iv) ଚତୁର୍ଥାଶଂକ ବିଚ୍ୟୁତି
Answer:
(i) ମାଧ୍ୟ ବିଚ୍ୟୁତି
୬। କେଉଁ ବିଚ୍ଛୁରଣ କେବଳ ମଧ୍ଯମାନଠାରୁ ନିର୍ଣ୍ଣୟ କରାଯାଏ ?
(i) ମାଧ୍ୟ ବିଚ୍ୟୁତି
(ii) ବିସ୍ତାର
(iii) ମାନକ ବିଚ୍ୟୁତି
(iv) ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି
Answer:
(iii) ମାନକ ବିଚ୍ୟୁତି
![]()
୭। ମାନକ ବିଚ୍ୟୁତିର ବର୍ଗ ହେଉଛି –
(i) ମାଧ୍ୟ ବିଚ୍ୟୁତି
(ii) ବିସ୍ତାର
(iii) ମାନକ ବିଚ୍ୟୁତି
(iv) ପ୍ରସାରଣ
Answer:
(iv) ପ୍ରସାରଣ
୮। କେଉଁଟି ବିଚ୍ଛୁରଣର ଜ୍ୟାମିତିକ ପରିପ୍ରକାଶ ଅଟେ ?
(i) ମାଧ୍ୟ-ବିଚ୍ୟୁତି
(ii) ବାରମ୍ବାରତା ବକ୍ରରେଖା
(iii) ମାନକ ବିଚ୍ୟୁତି
(iv) ଲରେଞ୍ଜ ବକ୍ରରେଖା
Answer:
(iv) ଲରେଞ୍ଜ ବକ୍ରରେଖା
୯। ମାଧ୍ୟ ବିଚ୍ୟୁତି କେଉଁ ହାରାହାରିଠାରୁ ଗଣନା କରାଯାଏ ?
(i) ମାଧ୍ୟମାନ
(ii) ମଧ୍ୟମା
(iii) ଉଭୟ ମାଧ୍ୟମାନ ଓ ମଧ୍ୟମା
(iv) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer: (iii) ଉଭୟ ମାଧ୍ଯମାନ ଓ ମଧ୍ୟମା
୧୦। ମାଧବିଚ୍ୟୁତି କେଉଁ ମଧ୍ଯକଠାରୁ ଗଣନା କରାଯାଏ ?
(i) ମାଧ୍ୟମାନ
(ii) ମଧ୍ୟମା
(iii) ଗରିଷ୍ଠକ
(iv) ଉପରୋକ୍ତ ସମସ୍ତ ମଧ୍ୟକ
Answer:
(iv) ଉପରୋକ୍ତ ସମସ୍ତ ମଧ୍ଯକ
୧୧। କେଉଁ ମଧ୍ଯକଠାରୁ ଲବ୍ଧାଙ୍କ ବିଚ୍ୟୁତିର ବର୍ଗର ଯୋଗଫଳ ସର୍ବନିମ୍ନ ?
(i) ମାଧ୍ୟମାନ
(ii) ମଧ୍ୟମା
(iii) ଗରିଷ୍ଠକ
(iv) ଚତୁର୍ଥାଂଶକ
Answer:
(i) ମାଧ୍ୟମାନ
![]()
୧୨। ଭାଗବିଭକ୍ତ ତଥ୍ୟାବଳୀର ବିସ୍ତାର କେଉଁ ଲବ୍ଧାଙ୍କ ଦ୍ବୟର ଅନ୍ତରଫଳ ଦ୍ବାରା ଆକଳନ ହୋଇଥାଏ ?
(i) ବୃହତ୍ତର ସଂଭାଗର ନିମ୍ନସୀମା ଓ କ୍ଷୁଦ୍ରତମ ସଂଭାଗର ଉର୍ଦ୍ଧ୍ୱସୀମା
(ii) ବୃହତ୍ତର ସଂଭାଗର ଉର୍ଦ୍ଧ୍ୱସୀମା ଓ କ୍ଷୁଦ୍ରତମ ସଂଭାଗର ଊର୍ଦ୍ଧ୍ୱସୀମା
(iii) ବୃହତ୍ତର ସଂଭାଗର ଉର୍ଦ୍ଧ୍ୱସୀମା ଓ କ୍ଷୁଦ୍ରତମ ସଂଭାଗର ନିମ୍ନସୀମା
(iv) ବୃହତ୍ତର ସଂଭାଗର ନିମ୍ନସୀମା ଓ କ୍ଷୁଦ୍ରତମ ସଂଭାଗର ନିମ୍ନସୀମା
Answer:
(ii) ବୃହତ୍ତର ସଂଭାର ଉର୍ଦ୍ଧ୍ୱସୀମା ଓ କ୍ଷୁଦ୍ରତମ ସଂଭାଗର ଉର୍ଦ୍ଧ୍ୱସୀମା
B. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :
୧। କୌଣସି ବଣ୍ଟନର ବିଚ୍ଛୁରଣ ତାହାର _____________________ ର ଚତୁଃପାର୍ଶ୍ଵରେ ବିଚ୍ଛୁରିତ ହେବାର ସୂଚନା ପ୍ରଦାନ କରେ
Answer:
କେନ୍ଦ୍ରୀୟମାନ
୨। ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ______________________ ସୂତ୍ର ସାହାଯ୍ୟରେ ନିର୍ଣ୍ଣୟ କରାଯାଏ।
Answer:
\(\frac{\theta_3-\theta_1}{2}\)
୩। ମାଧ୍ୟମାନଠାରୁ ଲବ୍ଧାଙ୍କମାନଙ୍କର ବିଚ୍ୟୁତିର ଯୋଗଫଳ ____________________ ।
Answer:
ଶୂନ୍ୟ
୪। ____________________ ମଧ୍ଯକଠାରୁ ଲବ୍ଧାଙ୍କମାନଙ୍କ ବିଚ୍ୟୁତିର ପରମମାନର ଯୋଗଫଳ ସର୍ବନିମ୍ନ।
Answer:
ମଧ୍ୟମା
୫। କୌଣସି ବଣ୍ଟନର ବିସ୍ତାର ତାହାର ମାନକ ବିଚ୍ୟୁତିଠାରୁ ___________________ ।
Answer:
ବୃହତ୍ତର
୬। ___________________ ବିଚ୍ଛୁରଣ ମାପଙ୍କରେ ବାରମ୍ବାରତା ବ୍ୟବହାର ହୋଇ ନ ଥାଏ।
Answer:
ବିସ୍ତାର
![]()
୭। ___________________ ବିଚ୍ଛୁରଣ ମାପଙ୍କ ଚରମ ଲବ୍ଧାଙ୍କ ଦ୍ଵାରା ବହୁଳ ପ୍ରଭାବିତ ଅଟେ।
Answer:
ବିସ୍ତାର
୮। ବିତରଣର ବୃହତ୍ତମ ଓ କ୍ଷୁଦ୍ରତମ ଲବ୍ଧାଙ୍କଦ୍ବୟର ଅନ୍ତରକୁ ________________ କହନ୍ତି ।
Answer:
ବିସ୍ତାର
୯। ____________________ ବିଚ୍ଛୁରଣ ମାପରେ ବିଦ୍ୟୁତିର ପରମମାନକୁ ବିଚାରକୁ ନିଆଯାଏ।
Answer:
ବିସ୍ତାର
୧୦। ________________________ ଚତୁର୍ଥାଂଶକ ମଧ୍ୟମା ସହିତ ସମାନ।
Answer:
ମଧ୍ୟଚତୁର୍ଥାଂଶ
୧୧। ______________________ ବିଚ୍ୟୁତିର ବୀଜଗାଣିତିକ ପ୍ରତିପାଦନ କ୍ଷମତା ଥାଏ ।
Answer:
ମାନକ ବିଚ୍ୟୁତି
୧୨। ______________________ ବିଚ୍ୟୁତି ହାରାହାରିରୁ ଧନାତ୍ମକ ଓ ଋଣାତ୍ମକ ଚିହ୍ନ ଛାଡ଼ି ପ୍ରତ୍ୟେକ ଲବ୍ଧଶଙ୍କର ବିଚ୍ୟୁତି ବାହାର କରିଥାଏ।
Answer:
ମାଧ୍ୟବିଚ୍ୟୁତି
C. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
୧। ବିସ୍ତାର କ’ଣ ?
Answer:
ରାଶିମାଳାର ବୃହତ୍ତମ ଓ କ୍ଷୁଦ୍ରତମ ଲବ୍ଧାଙ୍କ ଦ୍ଵୟର ଅନ୍ତରଫଳକୁ ବିସ୍ତାର କୁହାଯାଏ।
୨। ମାଧ୍ୟବିଚ୍ୟୁତି କ’ଣ ?
Answer:
ଗୋଟିଏ ବିତରଣରେ ଲବ୍ଧାଙ୍କମାନଙ୍କଠାରୁ ମାଧମାନ ବା ମଧ୍ୟମାର ପରମ ବିଚ୍ୟୁତି ଗୁଡ଼ିକର ମାଧ୍ଯମାନକୁ ମଧ୍ୟ ବିଚ୍ୟୁତି କୁହାଯାଏ।
![]()
୩। ମାନକ ବିଚ୍ୟୁତି କ’ଣ ?
Answer:
ଗୋଟିଏ ବିତରଣରେ ମାଧମାନ ଓ ଲବ୍ଧାଙ୍କ ମାନଙ୍କର ଅନ୍ତରର ବର୍ଗର ମାଧ୍ଯମାନର ଧନାତ୍ମକ ବର୍ଗମୂଳକୁ ମାନକ ବିଚ୍ୟୁତି କୁହାଯାଏ।
୪। ବିଚରଣ ଗୁଣାଙ୍କ କ’ଣ ?
Answer:
ମାଳକ ବିଚ୍ୟୁତି ଓ ମାଧ୍ଯମାନର ଶତକଡ଼ା ଅନୁପାତକୁ ବିଚରଣ ଗୁଣାଙ୍କ କୁହାଯାଏ।
୫। ପ୍ରସରଣ କ’ଣ ?
Answer:
ମାନକ ବିଦ୍ୟୁତିର ବର୍ଗକୁ ପ୍ରସରଣ କୁହାଯାଏ।
୬। ଚତୁର୍ଥାଂଶକର ବିଚ୍ୟୁତି କାହାକୁ କୁହାଯାଏ ?
Answer:
ଉର୍ଦ୍ଧ୍ବ ଓ ଅଧଃ ଚତୁର୍ଥାଂଶକର ଅନ୍ତରଫଳର ହାରାହାରିକୁ ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି କୁହାଯାଏ ।
୭। ବିସ୍ତାର କ’ଣ ?
Answer:
ବିତରଣ ମାଳାର ସର୍ବବୃହତ୍ ଓ ସର୍ବନିମ୍ନ ଲବ୍ଧାଙ୍କ ଦ୍ବୟର ଅନ୍ତରଫଳକୁ ବିସ୍ତାର କୁହାଯାଏ।
୮। ବିସ୍ତାରର ଗୁଣାଙ୍କ କ’ଣ ?
Answer:
ବିତରଣ ମାଳାର ସର୍ବାଧିକ ମୂଲ୍ୟ ଓ ସର୍ବନିମ୍ନ ମୂଲ୍ୟର ବିୟୋଗ ଓ ଯୋଗର ଅନୁପାତକୁ ବିସ୍ତାରର ଗୁଣାଙ୍କ କୁହାଯାଏ।’
୯। ବିଚ୍ଛୁରଣ କାହାକୁ କୁହାଯାଏ ?
Answer:
କୌଣସି ପର୍ଯ୍ୟବେକ୍ଷଣ ବା ତଥ୍ୟାବଳୀରେ ଲବ୍ଧାଙ୍କ ଗୁଡ଼ିକ କେନ୍ଦ୍ରୀୟ ମାପକରେ ଉଭୟ ପାର୍ଶ୍ଵରେ କିପରି ଭାବରେ ବିଚ୍ଛୁରିତ ହୋଇ ରହିଛନ୍ତି, ତାହାକୁ ବିଚ୍ଛୁରଣ କୁହାଯାଏ।
୧୦। ବିଜୁରଣର ଯେକୌଣସି ଗୋଟିଏ ଆଭିମୁଖ୍ୟ ଲେଖ ।
Answer:
ବିଚ୍ଛୁରଣ କୌଣସି ରାଶିମାଳାର ହାରାହାରି ବିଭିନ୍ନତା ପରିପ୍ରକାଶ କରିଥାଏ।
![]()
୧୧। ବିଜୁରଣ ମାର୍ଗର ବିଶୁଦ୍ଧ ପରିମାପ କ’ଣ ?
Answer:
ବିଚ୍ଛୁରଣର ପରିମାପ ଯାହାକୁ ବିତରଣ ମାଳାର ମୌଳିକ ଏକକରେ ପ୍ରକାଶ କରାଯାଏ, ତାହାକୁ ବିଶୁଦ୍ଧ ପରିମାପ କୁହାଯାଏ ।
୧୨। ବିଜୁରଣ ମାପର ଆପେକ୍ଷିକ ପରିମାପ କ’ଣ ?
Answer:
ତଥ୍ୟାବଳୀର ପରିବର୍ତ୍ତନୀୟତା ଶତକଡ଼ଶ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଗଲେ ତାହାକୁ ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ପରିମାପ କୁହାଯାଏ ।
୧୩। ବିସ୍ତାର ଯେକୌଣସି ଗୋଟିଏ ଉପକାରିତା ବର୍ଣ୍ଣନା କର ?
Answer:
ପାଣିପାଗର ଭବିଷ୍ୟତ ସୂଚନା ପ୍ରଦାନ କରେ।
୧୪। ବିଜୁରଣର କେଉଁ ପରିମାପକୁ ହାରାହାରି ବିଚ୍ୟୁତି କୁହାଯାଏ ?
Answer:
ମାଧ୍ୟ-ବିଚ୍ୟୁତି
୧୫। ମାଧବିଚ୍ୟୁତିର କୌଣସି ଗୋଟିଏ ବ୍ୟବହାର ଲେଖ।
Answer:
ଏହା ବ୍ୟବସାୟିକ ଉତ୍ଥାନ ପତନର ଗଣନା କ୍ଷେତ୍ରରେ ବିଶେଷ ଉପଯୋଗୀ।
୧୬। ଏକ ଅବାଧ ସଂଭାଗ ବିସ୍ତାର କ୍ଷେତ୍ରରେ କେଉଁ ପରିମାପକ ସବୁଠାରୁ ଅଧିକ ପ୍ରଯୁଜ୍ୟ ଅଟେ ?
Answer:
ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ।
୧୭। ବିଚରଣ ଗୁଣାଙ୍କ ନିର୍ଣ୍ଣୟ ସୂତ୍ରଟି କ’ଣ ?
Answer:
\(C . V=\frac{6}{\bar{X}} \times 100\)
୧୮। ଯଦି ବିଚରଣର ମାନକ ବିଚ୍ୟୁତି କମ୍ ହୁଏ, ତାହାହେଲେ ବିତରଣର ବିଚ୍ଛୁରଣ କ’ଣ ହୁଏ ?
Answer:
ସ୍ୱଳ୍ପ ।
୧୯। ଆଦର୍ଶ ବିଜୁରଣର ପରିମାପଟି କ’ଣ ?
Answer:
ମାନକ ବିଚ୍ୟୁତି
୨୦ । ଚତୁର୍ବିଂଶକ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ ମୂଲ୍ୟ ଗୋଟିଏ ପରିସଂଖ୍ୟାନ ବଣ୍ଟନମାଳାକୁ ସମାନ ଚାରି ଭାଗରେ ଭାଗ କରେ ତାହାକୁ ଚତୁର୍ଥାଂଶକ କୁହାଯାଏ ।
୨୧। ମାଧବିଚ୍ୟୁତି କାହିଁକି ଖୁବ୍ କମ୍ ବ୍ୟବହାର କରାଯାଏ ?
Answer:
କାରଣ ଏହାର ନିର୍ଣ୍ଣୟ ସମୟରେ ‘+’ ଓ ‘−’ ଚିହ୍ନକୁ ଉପେକ୍ଷା କରାଯାଇଥାଏ।
![]()
୨୨। କେଉଁ ବିଚ୍ଛୁରଣ ପରିମାପକଟି ସର୍ବୋତ୍କୃଷ୍ଟ ଅଟେ ?
Answer:
ମାନକ ବିଚ୍ୟୁତି ।
୨୩। ମାନକ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ ନିର୍ୟୟ ସୂତ୍ରଟି କ’ଣ ?
Answer:

= \(\frac{6}{\bar{X}}\)
୨୪। ମାନକ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ କ’ଣ ?
Answer:
ଦୁଇଟି ରାଶିମାଳାର ମାନକ ବିଦ୍ୟୁତିର ବିଭିନ୍ନତାର ଆପେକ୍ଷିତ ପରିମାପ ହେଉଛି ମାନକ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ।
୨୫। ମାଧ୍ୟ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ କ’ଣ ?
Answer:
କୌଣସି ତଥ୍ୟାବଳୀର ମାଧ୍ୟ ବିଚ୍ୟୁତିକୁ ସଂପୃକ୍ତ ହାରାହାରି ମୂଲ୍ୟ ଦ୍ଵାର ଭାଗକୁ ମାଧ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ କୁହାଯାଏ।
୨୬। ମାଧ୍ୟ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ ନିର୍ଣ୍ଣୟ କରିବାର ସୂତ୍ରଟି କ’ଣ ?
Answer:
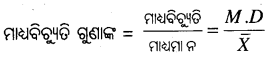
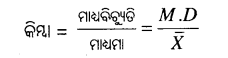
୨୭ । ମାଧ୍ଯମାନ ୨୦ ଏବଂ ମାନକ ବିଚ୍ୟୁତି ୪ ହେଲେ ବିଚରଣ ଗୁଣାଙ୍କ ହେବ କେତେ ?
Answer:
୨୦ ( ବିଚରଣ ଗୁଣାଙ୍କ (C.V) = \(\left.\frac{6}{\bar{X}} \times 100=\frac{4}{20} \times 100=20\right)\)
D. ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକ ଭୁଲ କି ଠିକ୍ ଲେଖ । ରେଖାଙ୍କିତ ଅଂଶର ପରିବର୍ତ୍ତନ ନ କରି ଆବଶ୍ୟକ ସ୍ଥଳେ ସଂଶୋଧନ କର ।
୧। ମାନକ ବିଚ୍ୟୁତିର ବର୍ଗ ମୂଳକୁ ପ୍ରସରଣ କୁହାଯାଏ ।
Answer:
ମାନକ ବିଚ୍ୟୁତିର ବର୍ଗକୁ ପ୍ରସରଣ କୁହାଯାଏ।
![]()
୨। ବିଚ୍ଛୁରଣ ଯେତେ ବେଶୀ ହୁଏ ତଥ୍ୟାବଳୀର ସଂଗତି ସେତେ ବେଶି ହୁଏ ।
Answer:
ବିଚ୍ଛୁରଣ ଯେତେ ବେଶୀ ହୁଏ ତଥ୍ୟାବଳୀର ସଂଗତି ସେତେ କମ୍ ହୁଏ ।
୩। ବିଚ୍ଛୁରଣ ଗୁଣାଙ୍କ ବିଜୁରଣର ଏକ ବିଶୁଦ୍ଧ ପରିମାପ ଅଟେ ।
Answer:
ବିଚ୍ଛୁରଣ ଗୁଣାଙ୍କ ବିଚ୍ଛୁରଣର ଏକ ଆପେକ୍ଷିକ ପରିମାପ ଅଟେ ।
୪। ପ୍ରସାରଣ ମାନକ ବିଚ୍ୟୁତିର ବର୍ଗମୂଳ ସଙ୍ଗେ ସମାନ ।
Answer:
ପ୍ରସାରଣ ମାନକ ବିଚ୍ୟୁତିର ବର୍ଗ ସଙ୍ଗେ ସମାନ ।
୫। ବିଜୁରଣର ପରିମାପକୁ ପ୍ରଥମ ଶ୍ରେଣୀର ହାରାହାରି କୁହାଯାଏ।
Answer:
ବିଚ୍ଛୁରଣର ପରିମାପକୁ ଦ୍ଵିତୀୟ ଶ୍ରେଣୀର ହାରାହାରି କୁହାଯାଏ।
୬। ବିଜୁରଣର ଆପେକ୍ଷିକ ପରିମାପକୁ ମୌଳିକ ଏକକରେ ପ୍ରକାଶ କରାଯାଏ।
Answer:
ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ପରିମାପକୁ ଶତକଡ଼ାରେ ପ୍ରକାଶ କରାଯାଏ।
୭। ଦୁଇଟି ବିତରଣ ମାଳାର ପରିବର୍ତ୍ତନୀୟ ତୁଳନା କରିବା ପାଇଁ ବିଶୁଦ୍ଧ ପରିମାପ ବ୍ୟବହାର ହୋଇଥାଏ।
Answer:
ଦୁଇଟି ବିତରଣ ମାଳାର ପରିବର୍ତ୍ତନୀୟ ତୁଳନା କରିବା ପାଇଁ ଆପେକ୍ଷିକ ପରିମାପ ବ୍ୟବହାର ହୋଇଥାଏ।
୮। ବିତରଣ ମାଳାର ସର୍ବ ବୃହତ୍ ଓ ସର୍ବ କନିଷ୍ଠ ଲବ୍ଧାଙ୍କଦ୍ୱୟର ଅନ୍ତରଫଳକୁ ବିସ୍ତାର କୁହାଯାଏ।
Answer:
ଠିକ୍
୯। ଗୋଟିଏ ବଣ୍ଟନରେ ବିସ୍ତାର ନିର୍ଣ୍ଣୟରେ ୫୦% ଲବ୍ଧାଙ୍କ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ।
Answer:
ଗୋଟିଏ ବଣ୍ଟନରେ ବିସ୍ତାର ନିର୍ଣ୍ଣୟରେ ୧୦୦% ଲବ୍ଧାଙ୍କ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ।
![]()
୧୦। ବିସ୍ତାର ନିଶ୍ଚିୟ ବିତରଣ ମାଳାର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ।
Answer:
ବିସ୍ତାର ନିର୍ଣ୍ଣୟ ବିତରଣ ମାଳାର ସର୍ବବୃହତ୍ ଓ ସର୍ବନିମ୍ନ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟ ବସିତ।
୧୧। ମାଧ୍ୟ ବିଚ୍ୟୁତି ଚରମ ଲବ୍ଧାଙ୍କ ଦ୍ୱାରା ବିଶେଷ ପ୍ରଭାବିତ ହୋଇଥାଏ।
Answer:
ବିସ୍ତାର ଚରମ ଲବ୍ଧାଙ୍କ ଦ୍ଵାରା ବିଶେଷ ପ୍ରଭାବିତ ହୋଇଥାଏ।
୧୨। ଚତୁର୍ଥ ଚତୁର୍ଥାଂଶକ ହେଉଛି ମଧ୍ଯମା।
Answer:
ଦ୍ବିତୀୟ ଚତୁର୍ଥାଂଶକ ହେଉଛି ମଧ୍ଯମା ।
୧୩। ମାଧ୍ୟ ବିଚ୍ୟୁତି କେବଳ ମାଧ୍ଯମାନକୁ ବ୍ୟବହାର କରିଥାଏ।
Answer:
ମାଧ୍ୟବିଚ୍ୟୁତି ମାଧ୍ୟମାନ, ମଧ୍ୟମା ଓ ଗରିଷ୍ଠକକୁ ବ୍ୟବହାର କରିଥାଏ।
୧୪। ବିସ୍ତାର ଯେ କୌଣସି ହାରାହାରିରୁ ଗଣନା କରାଯାଏ।
Answer:
ମାଧବିଚ୍ୟୁତି ବିସ୍ତାର ଯେ କୌଣସି ହାରାହାରିରୁ ଗଣନା କରାଯାଏ।
୧୫। ମାଧବିଚ୍ୟୁତି ଏକ ସର୍ବୋକୃଷ୍ଟ ବିଚ୍ଛୁରଣ ପରିମାପକ।
Answer:
ମାନକ ବିଚ୍ୟୁତି ଏକ ସର୍ବୋତ୍କୃଷ୍ଟ ବିଚ୍ଛୁରଣ ପରିମାପକ ।
୧୬। ମାନକ ବିଚ୍ୟୁତି ମଧ୍ଯମାକୁ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟରେ ବ୍ୟବହାର କରିଥାଏ।
Answer:
ମାନକ ବିଚ୍ୟୁତି ମାଧବିଚ୍ୟୁତି ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟରେ ବ୍ୟବହାର କରିଥାଏ।
୧୭। ଯଦି ବିଜୁରଣର ମାନକ ବିଚ୍ୟୁତି କମ୍ ହୁଏ ତା’ ହେଲେ ବିତରଣର ବିଚ୍ଛୁରଣ ଅଧ୍ବକ ହୁଏ ।
Answer:
ଯଦି ବିଚ୍ଛୁରଣର ମାନକ ବିଚ୍ୟୁତି କମ୍ ହୁଏ ତା’ ହେଲେ ବିତରଣର ବିଚ୍ଛୁରଣ ସ୍ଵଳ୍ପ ହୁଏ।
![]()
୧୮। ଯଦି ବଣ୍ଟନ ‘କ’ର ମାଧ୍ୟମାନ ଓ ମାନକ ବିଚ୍ୟୁତି ଯଥାକ୍ରମେ ବଣ୍ଟନ ‘ଖ’ର ମାଧ୍ୟମାନ ଓ ମାନକ ବିଚ୍ୟୁତି ଅପେକ୍ଷା କ୍ଷୁଦ୍ରତର ହୋଇଥା’ନ୍ତି, ତା’ହେଲେ ବଣ୍ଟନ ‘କ’ ବଣ୍ଟନ ‘ଖ’ ଅପେକ୍ଷା ଅଧିକ ସୁସଂଗତ ହୋଇଥାଏ।
Answer:
ଠିକ୍
ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
E. ନିମ୍ନଲିଖ ପ୍ରଶ୍ନମାନଙ୍କ ଉତ୍ତର ଦୁଇଟି / ତିନୋଟି ବାକ୍ୟ ମଧ୍ଯରେ ଦିଅ ।
୧। ବିଚ୍ଛୁରଣ କ’ଣ ?
Answer:
କୌଣସି ବଣ୍ଟନରେ ଲବ୍ଧାଙ୍କ ଗୁଡ଼ିକ କେନ୍ଦ୍ରୀୟମାନ ବା ମଧ୍ଯକର ଚତୁଃପାର୍ଶ୍ଵରେ କିପରି ଭାବେ ବିଚ୍ଛୁରିତ ହୋଇ ରହିଛନ୍ତି, ତାହାକୁ ବିଚ୍ଛୁରଣ କୁହାଯାଏ । ବିଚ୍ଛୁରଣ ଯେତେ ବେଶୀ, ତଥ୍ୟାବଳୀର ସଙ୍ଗତି ସେତେ କମ୍ ଓ ବିଚ୍ଛୁରଣ ଯେତେ କମ୍ ତଥ୍ୟାବଳୀର ସଙ୍ଗତି ସେତେ ବେଶି ହେବ ବୋଲି ବିଚାର କରାଯାଏ। ବିଜୁରଣର ମାପକ ଦ୍ଵିତୀୟ କ୍ରମର ମଧ୍ୟକ। ବିଚ୍ଛୁରଣର ମାପକ ଗୁଡ଼ିକୁ ଦୁଇଟି ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଥାଏ, ଯଥା – (୧) ବିଚ୍ଛୁରଣର ବିଶୁଦ୍ଧ ପରିମାପ, (୨) ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ପରିମାପ।
୨। ବିସ୍ତାର କ’ଣ ?
Answer:
ବିଚ୍ଛୁରଣର ପରିମାପକମାନଙ୍କ ମଧ୍ୟରୁ ବିସ୍ତାର ସବୁଠାରୁ ସହଜ। ଏହା ବାରମ୍ବାରତା ପରିବଣ୍ଟନ ସାରଣୀରେ ବୃହତ୍ତମ ଓ କ୍ଷୁଦ୍ରତମ ଲବ୍ଧାଙ୍କ ଦ୍ବୟର ଅନ୍ତରଫଳକୁ ବୁଝାଇଥାଏ। ବିସ୍ତାରମାନ ଅଧିକ ହେଲେ ବିଚ୍ଛୁରଣ ଅଧ୍ବକ ଓ ବିସ୍ତାରର ମାନ କମ୍ ହେଲେ ବିଚ୍ଛୁରଣ କମ୍ ହୁଏ। ବିସ୍ତାର କେବଳ ସର୍ବାଧକ ଓ ସର୍ବନିମ୍ନ ଲବ୍ଧାଙ୍କ ଦ୍ଵୟ ଉପରେ ନିର୍ଭରଶୀଳ ହୋଇଥିବାରୁ ଏହାକୁ ବିଚ୍ଛୁରଣର ଉତ୍ତମ ମାପକ ରୂପେ ଗ୍ରହଣ କରାଯାଏ ନାହିଁ ।
ଏହାର ଆପେକ୍ଷିକ ପରିମାପକ =\(\frac{L-S}{L+S}\) । C ହେଉଛି ବୃହତ୍ତମ ଲବ୍ଧାଙ୍କ ଏବଂ S ହେଉଛି କ୍ଷୁଦ୍ରତମ ଲବ୍ଧାଙ୍କ । ସାଧାରଣତଃ ଗୁଣ ନିୟନ୍ତ୍ରଣ ଓ ପାଣିପାଗର ସୂଚନା କ୍ଷେତ୍ରରେ ଏହା ବ୍ୟବହୃତ ହୁଏ।
୩। ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ପରିମାପ କ’ଣ ?
Answer:
କିଛି ଆପେକ୍ଷିକ ମୂଲ୍ୟ ବା ଶତକଡ଼ା ମାଧ୍ୟମରେ ତଥ୍ୟାବଳୀର ପରିବର୍ତ୍ତନୀୟତା ପ୍ରକାଶକୁ ବିଜୁରଣର ଆପେକ୍ଷିକ ପରିମାପ ବୋଲି କୁହାଯାଏ। ଆପେକ୍ଷିକ ପରିମାପକୁ ଅନୁପାତ ବା ଶତକଡ଼ାରେ ସ୍ଥିର କରାଯାଏ। ସେଥିପାଇଁ ଏହି ପରିମାପକୁ ସ୍ଵତନ୍ତ୍ର ଏକକର ବାସ୍ତବ ସଂଖ୍ୟା ବୋଲି କୁହାଯାଏ। ଏହା ସର୍ବାଧିକ ମୂଲ୍ୟ ଓ ସର୍ବନିମ୍ନ ମୂଲ୍ୟର ଅନୁପାତ ଓ ସେମାନଙ୍କର ସମ୍ମିଶ୍ରଣକୁ ବୁଝାଏ। ଦୁଇଟି ରଣ ମାଳାର ପରିବର୍ତ୍ତନୀୟତା ତୁଳନା କରିବା ପାଇଁ ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ମାପର ହିସାବ ଏକାନ୍ତ ଆବଶ୍ୟକ ।
![]()
୪। ମାନକ ବିଚ୍ୟୁତି କ’ଣ ?
Answer:
ମାନକ ବିଚ୍ୟୁତି ବିଜୁରଣର ଅନ୍ୟ ଏକ ପରିମାପକ। ଏହି ତତ୍ତ୍ଵକୁ ୧୮୨୩ ମସିହାରେ କାର୍ଲ-ପିଅରସନ ପ୍ରଥମେ ପ୍ରତିପାଦନ କରିଥିଲେ । ଗୋଟିଏ ବାରମ୍ବାରତା ବିତରଣ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ଓ ଲଜ୍ଜାଙ୍କମାନଙ୍କର ଅନ୍ତରର ବର୍ଗର ମାଧ୍ଯମାନର ବର୍ଗ ମୂଳକୁ ମାନକ ବିଚ୍ୟୁତି କୁହାଯାଏ।
ଯହିଁରେ ୬ = ମାନକ ବିଚ୍ୟୁତି, N = ବାରମ୍ବାରତାର ସମଷ୍ଟି ∑d² = ବିଭିନ୍ନ ଲଜ୍ଜାଙ୍କର ଗାଣିତିକ ମାଧମାନର ବିଚ୍ୟୁତିର ବର୍ଗର ସମଷ୍ଟି ମାନକ ବିଚ୍ୟୁତିର ଆପେକ୍ଷିକ

ଯେତେବେଳେ ଦୁଇଟି ବା ତହିଁରୁ ଅଧିକ ମାଳା ମଧ୍ଯରେ ତୁଳନା କରିବାକୁ ପଡ଼େ, ଏହି ମାନକ ବିଦ୍ୟୁତିର ଆପେକ୍ଷିକ ପରିମାପ ସେତେବେଳେ ବ୍ୟବହୃତ ହୋଇଥାଏ। ଏହାକୁ ମଧ୍ୟ ବିଚରଣର ଗୁଣାଙ୍କ ମଧ୍ୟ କୁହାଯାଏ। ଯେଉଁ ମାଳାର ଆପେକ୍ଷିକ ମୂଲ୍ୟ ଅଧିକ ହୋଇଥାଏ, ସେହି ମାଳାର ବିଚ୍ଛୁରଣ ଅଧିକ ହୋଇଥାଏ।
୫। ବିଜୁରଣ ପରିମାପକ କିପରି ମନୋନୟନ କରିବ ?
Answer:
ବିଚ୍ଛୁରଣ ପ୍ରତ୍ୟେକ ପରିମାପକର କିଛି ନା କିଛି ସୁ-ଗୁଣ ଓ ଦୁର୍ଗୁଣ ରହିଛି । ସବୁ ପରିମାପକ ସବୁ କ୍ଷେତ୍ରରେ ପ୍ରଯୁଜ୍ୟ କହିବା ଠିକ୍ ନୁହେଁ । ବଣ୍ଟନର ବିଭିନ୍ନ ଦିଗ ପ୍ରତି ଦୃଷ୍ଟି ଦେଇ ବିଚ୍ଛୁରଣର ପରିମାପକ ମନୋନୟନ କରିବା ଉଚିତ୍। ଯେପରି ପାଣିପାଗ ସୂଚନା କ୍ଷେତ୍ରରେ ବା ଗୁଣ ନିୟନ୍ତ୍ରଣ କ୍ଷେତ୍ରରେ ବିସ୍ତାର ସବୁଠାରୁ ଅଧିକ ପ୍ରଯୁଜ୍ୟ । କିନ୍ତୁ ଏକ ଅବାଧ ସଂଭାଗ ବିସ୍ତାର ବିତରଣ କ୍ଷେତ୍ରରେ ଚତୁର୍ଥାଂଶକ ଅଧିକ ଉପଯୁକ୍ତ ପରିମାପକ ଅଟେ । ଯେହେତୁ ମାଧବିଚ୍ୟୁତି ‘–’ ଓ ‘+’ ଚିହ୍ନକୁ ଉପେକ୍ଷା କରିଥାଏ, ତେଣୁ ଏହି ବିଚ୍ଛୁରଣ ନିର୍ଣ୍ଣୟରେ ବହୁତ କମ୍ ବ୍ୟବହାର କରାଯାଏ । ମାନକ ବିଚ୍ୟୁତି ଏକ ଉତ୍ତମ ବିଚ୍ଛୁରଣ ପରିମାପକ ।
ଏହା ଉତ୍ତମ ବିଚ୍ଛୁରଣ ପରିମାପକର ସମସ୍ତ ଗୁଣ ବହନ କରିଥାଏ। ତଥ୍ୟାବଳୀର ବୈଷମ୍ୟ, ସହ ସମ୍ବନ୍ଧ ଇତ୍ୟାଦି ଆକଳନ କରିବାରେ ମାନକ ବିଚ୍ୟୁତି ଅପରିହାର୍ଯ୍ୟ ଅଟେ। ଯଦି ବିଭିନ୍ନ ପର୍ଯ୍ୟବେକ୍ଷଣ ବିଭିନ୍ନ ଏକକରେ ପ୍ରକାଶ କରାଯାଇଥାଏ ଓ ସେମାନଙ୍କର ତୁଳନାତ୍ମର୍କ ଅନୁଶୀଳନ ଦରକାର ହୁଏ, ସେ କ୍ଷେତ୍ରରେ ବିତରଣ ଗୁଣାଙ୍କ ବ୍ୟବହୃତ କରାଯାଇଥାଏ। ବଣ୍ଟନର ଅସମତାକୁ ଜ୍ୟାମିତିକ ଚିତ୍ର ଆକାରରେ ପ୍ରକାଶ କରିବାକୁ ହେଲେ ଲରେଞ୍ଜ ବକ୍ର ଉପଯୁକ୍ତ ବିଚ୍ଛୁରଣ ପରିମାପକ ଅଟେ।
୬। ମାଧ୍ୟ ବିଚ୍ୟୁତିର ସୁଗୁଣ ଲେଖ ?
Answer:
ମାଧବିଚ୍ୟୁତି ବିତରଣ ସାରଣର ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ଓ ଲବ୍କମାନଙ୍କର ଅନ୍ତରର ପରମମାନର ମାଧ୍ୟମାନକୁ ମାଧ୍ୟବିଚ୍ୟୁତି କୁହାଯାଏ।
- ଏହା ଖୁବ୍ ସହଜରେ ନିର୍ଣ୍ଣୟ କରିହୁଏ।
- ଏହାକୁ ସହଜରେ ବୁଝିହୁଏ।
- ଏହା ବିତରଣର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ।
- ଏହା ଚରମ ଲବ୍ଧାଙ୍କ ଦ୍ଵାରା ପ୍ରଭାବିତ ହୁଏ ନାହିଁ ।
![]()
୭। ମାଧ୍ୟବିଚ୍ୟୁତିର ଦୁର୍ଗୁଣଗୁଡ଼ିକ ଲେଖ ।
Answer:
- ଏହା ବ୍ୟର୍ଥବୋଧକ ବା ଅସ୍ପଷ୍ଟ ଅଟେ ।
- ଏହ ଗାଣିତିକ ପ୍ରକ୍ରିୟାରେ ପୁନଃ ବ୍ୟବହାର କରାଯାଏ ନାହିଁ ।
- ତୁଳନାତ୍ମକ ବିଶ୍ଳେଷଣ ପାଇଁ ଏହା ପ୍ରଯୁଜ୍ୟ ନୁହେଁ।
- ଏହା ନମୁନାର ପରିବର୍ତ୍ତନଦ୍ୱାରା ବିଶେଷ ଭାବେ ପ୍ରଭାବିତ ହୁଏ ।
୮। ମାନକ ବିଦ୍ୟୁତିର ସୁଗୁଣ ଓ ଦୁର୍ଗୁଣ ଲେଖ ?
Answer:
ମାନକ ବିଚ୍ୟୁତି ଏକ ଉତ୍ତର ବିଚ୍ଛୁରଣ ପରିମାପକ ବୋଲି ଗଣନା କରାଯାଏ, କାରଣ ଏହା ଅନେକ ଗୁଡ଼ିଏ ଭଲ ଗୁଣ ବହନ କରିଥାଏ। ସେଗୁଡ଼ିକ ହେଲା –
- ଏହା ବ୍ୟର୍ଥବୋଧକ ନୁହେଁ ।
- ଏହାର ନିର୍ଣ୍ଣୟ ବିତରଣର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ଆଧାରିତ ।
- ଏହା ଗାଣିତିକ ପ୍ରକ୍ରିୟାରେ ପୁନଃ ବ୍ୟବହାର କରାଯାଇଥାଏ। ଏହା ତଥ୍ୟାବଳୀର ବୈଷମ୍ୟ, ସହ ସମ୍ବନ୍ଦ, ସମାଶ୍ରିୟତା ଗୁଣାଙ୍କ ଇତ୍ୟାଦି ଆକଳନରେ ବ୍ୟବହୃତ ହୋଇଥାଏ।
- ଏହା ପ୍ରତିଚୟନର ହ୍ରାସ ବୃଦ୍ଧିଦ୍ୱାରା ବିଶେଷ ଭାବେ ପ୍ରଭାବିତ ହୋଇ ନ ଥାଏ।
- ବିତରଣର ମାଧମାନର ବିଶ୍ଵାସଯୋଗ୍ୟତା ମାନକ ବିଚ୍ୟୁତି ଦ୍ଵାରା ପ୍ରମାଣିତ ହୋଇଥାଏ।
ମାନକ ବିଚ୍ଯୁତିର ଦୁର୍ଗୁଣଗୁଡ଼ିକ ଲେଖ ।
- ଏହା ଗଣନା କରିବା ଓ ବୁଝିବା ସହଜ ନୁହେଁ।
- ଏହା ବିତରଣର ଚରମ ଲବ୍ଧାଙ୍କ ଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ।
- ଏହା ବିଭିନ୍ନ ଏକକରେ ପ୍ରକାଶିତ ବଣ୍ଟନର ତୁଳନାତ୍ମକ ଅନୁଶୀଳନ ପାଇଁ ପ୍ରଯୁଜ୍ୟ ନୁହେଁ ।
F. ପାଞ୍ଚଟି / ଛଅଟି ବାକ୍ୟରେ ସୀମିତ ରଖ୍ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ।
୧। ମାଧ୍ୟବିଚ୍ୟୁତି ଓ ମାନକ ବିଚୁ୍ୟତି
Answer:
କୌଣସି ବିତରଣ ସାରଣୀରେ ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କ ଅନ୍ତରର ପରମମାନର ମାଧ୍ୟମାନକୁ ମାଧ୍ୟବିଚ୍ୟୁତି କୁହାଯାଏ। ମାଧବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ଦ୍ଵାରା ହୋଇଥାଏ।
M.D ମାଧ୍ଯମାନଠାରୁ (MDX ) = \(\frac{\sum d x}{N}\)
M.D ମଧ୍ୟମା ଠାରୁ (MDm) = \(\frac{\sum d x}{m}\)
M.D ଗରିଷ୍ଠକ ଠାରୁ (MDz) = \(\frac{\sum d x}{z}\)
ଏଠାରେ ∑dX = ମାଧ୍ୟମାନ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ପରମମାନ
∑dm = ମଧ୍ୟମା ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ପରମମାନ
∑dz = ଗରିଷ୍ଠକ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ପରମମାନ
ମାଧ୍ୟବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ ସମୟରେ + ଓ – ଚିହ୍ନ ଗୁଡ଼ିକୁ ଉପେକ୍ଷା କରାଯାଇଥାଏ। ମାଧବିଚ୍ୟୁତି ଖୁବ୍ ସହଜରେ ନିଶ୍ଚୟ ଓ ହୃଦୟଙ୍ଗମ କରିହୁଏ । କିନ୍ତୁ ଗାଣିତିକ ପ୍ରକ୍ରିୟାରେ ଏହା ପୁନଃ ବ୍ୟବହୃତ ହୋଇପାରେ ନାହିଁ । କୌଣସି ବିତରଣ ସାରଣୀରେ ମାଧ୍ୟମାନ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ବର୍ଗର ମାଧମାନର ଧନାତ୍ମକ ବର୍ଗମୂଳକୁ ମାନକ ବିଚ୍ୟୁତି କୁହାଯାଏ। ସାଧାରଣତଃ ୬ (ସିଗ୍ମା) ଦ୍ଵାରା ସୂଚୀତ କରାଯାଏ।
\(6=\sqrt{\frac{\sum d X^2}{n}}\)![]()
ମାନକ ବିଚ୍ୟୁତି ବିଚ୍ଛୁରଣ ପରିମାପକମାନଙ୍କ ମଧ୍ୟରେ ଅଧିକ ଲୋକପ୍ରିୟ ପରିମାପକ ଅଟେ । ଏହା ବିତରଣର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ, ଅସ୍କଟ ନୁହେଁ ଏବଂ ଏହା ଗାଣିତିକ ପ୍ରକ୍ରିୟାରେ ପୁନଃ ବ୍ୟବହୃତ ହୋଇଥାଏ। କିନ୍ତୁ ଏହା ନିର୍ଣ୍ଣୟ କରିବା ଓ ହୃଦୟଙ୍ଗମ କରିବା ଏତେ ସହଜ ନୁହେଁ ।
୨। ବିସ୍ତାର ଓ ବିସ୍ତାର ଗୁଣାଙ୍କ
ଏହା ସର୍ବାପେକ୍ଷା ସହଜ, ସରଳ ଓ ସ୍କୁଳ ପରିମାପ ଅଟେ।
ବିସ୍ତାର = L – S
L= ସର୍ବାଧିକ ମୂଲ୍ୟ
S = ସର୍ବନିମ୍ନ ମୂଲ୍ୟ
ବିସ୍ତାର ବିଶୁଦ୍ଧ ପରିମାପକ ଅଟେ । ତେଣୁ ଏହା ତୁଳନାତ୍ମକ ଭାବରେ ବ୍ୟବହାର ହୋଇପାରେ ନାହିଁ । ଏହାର ଆପେକ୍ଷିକ ପରିମାପକ ନିମନ୍ତେ ବିସ୍ତାରର ଗୁଣାଙ୍କ ଅଧ୍ୟୟନ କରିବାକୁ ପଡ଼ିଥାଏ।
ବିସ୍ତାରର ଗୁଣାଙ୍କ = \(\frac{L-S}{L+S}\)
L = ସର୍ବାଧକ ମୂଲ୍ୟ, S = ସର୍ବନିମ୍ନ ମୂଲ୍ୟ।
୩। ମାଧ୍ୟ ବିଚ୍ୟୁତିର ଗୁଣାଙ୍କ ଓ ମାନକ ବିଚ୍ୟୁତିର ଗୁଣାଙ୍କ
Answer:
ଆପେକ୍ଷିକ ମାଧ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କରିବା ପାଇଁ କୌଣସି ତଥ୍ୟାବଳୀର ମାଧ ବିଚ୍ୟୁତିକୁ ସଂପୃକ୍ତ ହାରାହାରି ମୂଲ୍ୟ, ଯଥା ମାଧମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକଦ୍ଵାରା ଭାଗ କରାଯାଇଥାଏ। ଯଦି ବିଚ୍ୟୁତି ଗୁଡ଼ିକ ମାଧ୍ଯମାନରୁ ନିର୍ଣ୍ଣୟ କରାଯାଇଥବ, ତା’ହେଲେ ମାଧବିଚ୍ୟୁତିକୁ ସେହି ମାଧ୍ଯମାନ ଦ୍ଵାରା ଭାଗ କରିବାକୁ ପଡ଼ିଥାଏ, ସେହିପରି ମଧ୍ଯମା ବା ଗରିଷ୍ଠକ ଦ୍ଵାରା ନିର୍ଣ୍ଣୟ କରାଯାଇଥିଲେ ଏହା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ଦ୍ଵାରା ଭାଗ କରାଯାଇଥାଏ।
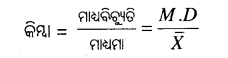
ଏହାକୁ ଶତକଡ଼ାରେ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେଲେ ଉକ୍ତ ସୂତ୍ରରେ ୧୦୦ ଗୁଣନ କରିବାକୁ ହୋଇଥାଏ।
ଦୁଇଟି ରାଶିମାଳାର ମାନକ ବିଦ୍ୟୁତିର ବିଭିନ୍ନତାର ଆପେକ୍ଷିକ ପରିମାପ ସ୍ଥିର କରିବା ପାଇଁ ମାନକ ବିଚ୍ୟୁତିର ଗୁଣାଙ୍କ ବ୍ୟବହାର କରାଯାଇଥାଏ ।
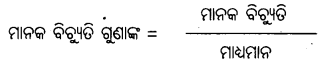
ଏହାକୁ ଶତକଡ଼ାରେ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେଲେ ଉକ୍ତ ସୂତ୍ରରେ 100 ଗୁଣନ କରିବାକୁ ହୋଇଥାଏ ।
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ବିଚ୍ଛୁରଣ କହିଲେ କ’ଣ ବୁଝ ? ବିଚ୍ଛୁରଣ ପରିମାପକଗୁଡ଼ିକ କ’ଣ ? ଏକ ଉତ୍ତମ ବିଚ୍ଛୁରଣ ପରିମାପକର ବୈଚିତ୍ରଗୁଡ଼ିକ ବର୍ଣ୍ଣନା କର ।
Answer:
କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତି; ଯଥା – ମାଧ୍ଯମାନ, ମଧ୍ୟମା ଓ ଗରିଷ୍ଠକ ଓ ତଥ୍ୟାବଳୀର ସମସ୍ତ ଲବ୍ଧାଙ୍କମାନଙ୍କର ପ୍ରତିନିଧ୍ୱ କରିଥାନ୍ତି । କିନ୍ତୁ ଏମାନଙ୍କଦ୍ୱାରା ତଥ୍ୟାବଳୀର ସମସ୍ତ ଅଭିଲକ୍ଷଣଗୁଡ଼ିକ ପ୍ରତିଫଳିତ ହୋଇ ନ ଥାଏ । ତଥ୍ୟାବଳୀର ସମସ୍ତ ଲବ୍ଧାଙ୍କମାନଙ୍କର ବିଷୟରେ ଅଧ୍ଯକ ଲକ୍ଷଣଗୁଡ଼ିକ ଜାଣିବା ପାଇଁ ବିଚ୍ଛୁରଣ ସମ୍ବନ୍ଧରେ ଅଧ୍ୟୟନ କରାଯାଏ । ମନେକର ଗୋଟିଏ ଶ୍ରେଣୀର ବାଳକମାନଙ୍କର ମାଧ୍ଯମାନ ମାର୍କ ଓ ବାଳିକାମାନଙ୍କର ମାଧ୍ଯମାନ ମାର୍କ ସମାନ ଅଟେ; ଯଥା – 37 ।
![]()
କିନ୍ତୁ ବାଳକ ତାଲିକାରେ ସର୍ବନିମ୍ନ ମାର୍କ 10 ଏବଂ ସର୍ବୋଚ୍ଚ ମାର୍କ 97 ଥିବା ସମୟରେ ବାଳିକା ତାଲିକାରେ ସର୍ବନିମ୍ନ ମାର୍କ 30 ଓ ସର୍ବୋଚ୍ଚ ମାର୍କ 95 ଅଛି । ଯଦିଓ ଉଭୟଙ୍କର ମାଧ୍ଯମାନ ମାର୍କ ସମାନ ତଥାପି ମାଧମାନ ତଥ୍ୟାବଳୀର ସମସ୍ତ ଲକ୍ଷଣଗୁଡ଼ିକ ଉପସ୍ଥାପିତ କରିପାରୁ ନାହିଁ । ବାଳିକାମାନଙ୍କର ମାର୍କ ମାଧ୍ୟମାନ ମାର୍କର ପାଖାପାଖ୍ ବିଚ୍ଛୁରିତ ହୋଇଥିଲାବେଳେ ବାଳକମାନଙ୍କର ମାର୍କ ଅଧ୍ବକ ବିଚ୍ଛୁରିତ ହୋଇରହିଛି । ଏଣୁ ବିଚ୍ଛୁରିତ ତଥ୍ୟାବଳୀ ସମ୍ବନ୍ଧରେ ଅଧିକ ଜ୍ଞାନ ପ୍ରଦାନ କରିଥାଏ ।
କୌଣସି ତଥ୍ୟାବଳୀରେ ଲବ୍ଧାଙ୍କଗୁଡ଼ିକ କେନ୍ଦ୍ରୀୟ ମାପକର ଉଭୟ ପାର୍ଶ୍ଵରେ କିପରିଭାବେ ବିଚ୍ଛୁରିତ ହୋଇ ରହିଛନ୍ତି, ତାହାକୁ ବିଚ୍ଛୁରଣ କୁହାଯାଏ । Prof. Spieges ଙ୍କ ମତରେ, “‘The degree to which numerical data tends to spread about an average value is called the variation or dispersion.” ସେହିପରି A.L. Bowleyଙ୍କ ମତରେ, “Dispersion is the measure of the variations of the item.”
ଏହିସବୁ ଦର୍ଶାଯାଇଥିବା ସଂଜ୍ଞାଗୁଡ଼ିକ ଅନୁଧ୍ୟାନ କଲେ ଜଣାପଡ଼ୁଛି ଯେ, ବିଚ୍ଛୁରଣ ତଥ୍ୟାବଳୀର ସଂଗତି (Consistency) ଉପରେ ଆଲୋକପାତ କରେ । ବଣ୍ଟନର ବିଚ୍ଛୁରଣ ଯେତେ ବେଶୀ ହେବ ତଥ୍ୟାବଳୀର ସଂଗତି ସେତେ କମ୍ ହେବ ଓ ବିଚ୍ଛୁରଣ ଯେତେ କମ୍ ତଥ୍ୟାବଳୀର ସଂଗତି ସେତେ ବେଶୀ ହେବ ବୋଲି ବିଚାର କରାଯାଇଥାଏ ।’
ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – (1) ବିଶୁଦ୍ଧ ପରିମାପ (Absolute measures of dispersion) ଓ (2) ଆପେକ୍ଷିକ ପରିମାପ (Relative measures of dispersion) । ବିଶୁଦ୍ଧ ପରିମାପଗୁଡ଼ିକ ହେଲା – ( 1 ) ବିସ୍ତାର (Range), (2) ଆନ୍ତଃ ଚତୁର୍ଥାଂଶକ (Inter-quartile range or Quartile deviation), (3) Flag (Mean deviation) ଓ (4) ମାନକ ବିଚ୍ୟୁତି (Standard deviation) ।,ସେହିପରି ଆପେକ୍ଷିକ ପରିମାପକଗୁଡ଼ିକ ହେଲା – (1) ବିଚରଣ ଗୁଣାଙ୍କ (Co-efficient of variation) ଏବଂ (2) ଲରେଞ୍ଜ୍ ବଜ୍ର (Lorenz curve) । ଆପେକ୍ଷିକ ବିଚ୍ଛୁରଣଦ୍ବାରା ଦୁଇ ବା ତତୋଽଧୂକ ବଣ୍ଟନର ସଂଗତିକୁ ତୁଳନା କରାଯାଇଥାଏ ।
ଏଠାରେ ପ୍ରଶ୍ନ ଉଠିପାରେ, ବିଚ୍ଛୁରଣର କେଉଁ ମାପକଟି ଉତ୍ତମ ଅଟେ । ପ୍ରତ୍ୟେକ ମାପକର କିଛି ନା କିଛି ଭଲ ବା ଖରାପ ଗୁଣ ଅଛି । ତଥାପି ଏକ ଉତ୍ତମ ବିଚ୍ଛୁରଣ ମାପକର ନିମ୍ନଲିଖିତ ଲକ୍ଷଣଗୁଡ଼ିକ ରିହବା ବିଧେୟ ।
- ଏହାକୁ ସହଜରେ କଷାଯାଇପାରୁଥ୍ ଓ ହୃଦୟଙ୍ଗମ କରିହେଉଥିବ ।
- ଏହା ବ୍ୟର୍ଥବୋଧକ ବା ଅସ୍ପଷ୍ଟ ହୋଇ ନ ଥିବ ।
- ସାଧାରଣ ଲୋକ ଏହାକୁ ବ୍ୟବହାର କରିପାରୁଥିବେ ।
- ଏହା ସମସ୍ତ ତଥ୍ୟାବଳୀର ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ ହୋଇଥବ ।
- ଏହାକୁ ଗାଣିତିକ ପ୍ରକ୍ରିୟାରେ ପୁନଃ ବ୍ୟବହାର କରାଯାଇପାରୁଥିବ ।
- ଏହା ଚରମ ଲବ୍ଧାଙ୍କଦ୍ୱାରା ପ୍ରଭାବିତ ହେଉ ନ ଥିବ ।
- (ଏହା ଅବାଧ ସଂଭାଗ ବିସ୍ତାର କ୍ଷେତ୍ରରେ ମଧ୍ୟ ଗଣନା କରାଯାଇପାରୁଥିବ ।
୨। ସଂକ୍ଷେପରେ ବିଚ୍ଛୁରଣର ପରିମାପକଗୁଡ଼ିକ ବର୍ଣ୍ଣନା କର ।
Answer:
କୌଣସି ପର୍ଯ୍ୟବେକ୍ଷଣରେ ଲବଧାଙ୍କଗୁଡ଼ିକ କେନ୍ଦ୍ରୀୟ ମାପକର ଉଭୟ ପାର୍ଶ୍ବରେ ଯେପରିଭାବରେ ବିଚ୍ଛୁରିତ ହୋଇ ରହିଛନ୍ତି, ତାହାକୁ ବିଚ୍ଛୁରଣ କୁହାଯାଏ । ତଥ୍ୟାବଳୀର ବିଚ୍ଛୁରଣ ନିର୍ଦ୍ଧାରଣ ପାଇଁ ବିଭିନ୍ନ ପଦ୍ଧତି ପରିମାପକ ଅନୁସରଣ କରାଯାଏ । ସେଗୁଡ଼ିକୁ ମୁଖ୍ୟତଃ ଦୁଇଗୋଟି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – ବିଶୁଦ୍ଧ ପରିମାପ (Absolute measures of dispersion) ଓ ଆପେକ୍ଷିକ ପରିମାପ (Relative measures of dispersion) ।
![]()
ବିଶୁଦ୍ଧ ପରିମାପକମାନଙ୍କ ମଧ୍ୟରୁ –
(1) ବିସ୍ତାର (Range)
(2) ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି (Quartile deviation)
(3) ମାଧ୍ୟବିଚ୍ୟୁତି (Mean deviation) ଓ
(4) ମାନକ ବିଚ୍ୟୁତି (Standard deviation) ଅନ୍ୟତମ ।
ଆପେକ୍ଷିକ ପରିମାପକମାନଙ୍କ ମଧ୍ୟରେ –
(1) ବିଚରଣ ଗୁଣାଙ୍କ (Coefficient of variation) ଓ
(2) ଲରେଞ୍ଜ୍ ବଜ୍ର (Lorenz curve) ବିଶେଷଭାବରେ ବ୍ୟବହୃତ ହୋଇଥାଏ ।
ଏଠାରେ ସେଗୁଡ଼ିକ ବିଷୟରେ ସଂକ୍ଷେପରେ ଆଲୋଚନା କରାଯାଇଛି ।
(1) ବିସ୍ତାର (Range) – ଏହା ବିତରଣ ସାରଣୀର ବୃହତ୍ତମ ଓ କ୍ଷୁଦ୍ରତମ ଲବ୍ଧାଙ୍କଦ୍ବୟର ଅନ୍ତରଫଳ ଅଟେ । ଅର୍ଥାତ୍ ବିସ୍ତାର (Range) = ବୃହତ୍ତମ ଲବ୍ଧାଙ୍କ – କ୍ଷୁଦ୍ରତମ ଲବ୍ଧାଙ୍କ
Or, R = L – S
ବିସ୍ତାରର ଗୁଣାଙ୍କ (Coefficient of Range) = \(\frac{L-S}{L+S}\)
ବିସ୍ତାରର ମାନ ଅଧ୍ଵ ହେଲେ ବିଚ୍ଛୁରଣ ଅଧ୍ବକ ଓ ବିସ୍ତାରର ମାନ କମ୍ ହେଲେ ବିଚ୍ଛୁରଣ କମ୍ ହୁଏ । ବିସ୍ତାର ସବୁଠାରୁ ସହଜ ପରିମାପକ ହେଲେ ମଧ୍ୟ ଏହାକୁ ବିଚ୍ଛୁରଣର ଉତ୍ତମ ମାପକରୂପେ ଗ୍ରହଣ କରାଯାଏ ।
(2) ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ବା ଆନ୍ତଃଚତୁର୍ଥାଂଶକ ବିସ୍ତାର (Quartile Deviation or Semi-Inter quartile Range) – ବିତରଣର ଊର୍ଦ୍ଧ୍ବ ଓ ଅଧଃ ଅନ୍ତରର ଅର୍ଦ୍ଧେକକୁ ଅନ୍ତଃଚତୁର୍ଥାଂଶ ବିସ୍ତାର ବା ଚତୁର୍ବିଂଶକ ବିଚ୍ୟୁତି ବୋଲି କୁହାଯାଏ । ସୁତରାଂ, IQR = Q3 = Q1 |
ଏବଂ \(\mathrm{QD}=\frac{\mathrm{Q}_3-\mathrm{Q}_1}{2}\)
ଏଠାରେ QD = ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି, Q3 = ଊର୍ଦ୍ଧ୍ବ ଚତୁର୍ଥାଂଶକ, Q1 = ଅଧଃ ଚତୁର୍ଥାଂଶକ । ଚତୁର୍ଥାଂଶ କର
ଗୁଣାଙ୍କ (Coefficient of QD) = \(\frac{\mathrm{Q}_3-\mathrm{Q}_1}{\mathrm{Q}_3+\mathrm{Q}_1}\)
ବିଚ୍ଛୁରଣର ମାପକ ହିସାବରେ ଏହା ସହଜ ଓ ଚରମ ଲବ୍ଧାଙ୍କମାନଙ୍କଦ୍ୱାରା ପ୍ରଭାବିତ ନ ହେଲେ ମଧ୍ୟ ଏହାର ବ୍ୟବହାର ବହୁତ ସଙ୍କୁଚିତ ହୋଇଥାଏ । କାରଣ ଏହା ସାରଣୀର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ ନୁହେଁ ।
(3) ମାଧ୍ୟବିଚ୍ୟୁତି (Mean deviation) – କୌଣସି ବିତରଣ ସାରଣୀରେ ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ପରମମାନର ମାଧ୍ଯମାନକୁ ମାଧବିଚ୍ୟୁତି (Mean deviation) କୁହାଯାଏ । ମାଧ୍ୟବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକଦ୍ୱାରା ହୋଇଥାଏ । ସୁତରାଂ;
MD ମାଧ୍ୟମାନଠାରୁ (MD x̄)=\(\frac{\Sigma \mathrm{dx}}{\mathrm{N}}\)
MD ମଧ୍ୟମାନଠାରୁ (MDm) = \(\frac{\Sigma \mathrm{dm}}{\mathrm{N}}\)
MD ଗରିଷ୍ଠକଠାରୁ (MDz) = \(\frac{\Sigma \mathrm{dz}}{\mathrm{N}}\)
ଏଠାରେ Σdx = ମାଧ୍ୟମାନ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ପରମମାନ ।
Σdm = ମଧ୍ୟମା ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ପରମମାନ ।
Σdz = ଗରିଷ୍ଠକ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ପରମମାନ ।
ମାଧ୍ୟବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ ସମୟରେ + ଓ – ଚିହ୍ନ ଗୁଡ଼ିକୁ ଉପେକ୍ଷା (Ignore) କରାଯାଇଥାଏ ।
ମାଧ୍ୟବିଚ୍ୟୁତି ଖୁବ୍ ସହଜରେ ନିର୍ଣ୍ଣୟ ଓ ହୃଦୟଙ୍ଗମ କରିହୁଏ । କିନ୍ତୁ ଗାଣିତିକ ପ୍ରକ୍ରିୟାରେ ଏହା ପୁନଃ ବ୍ୟବହୃତ ହୋଇପାରେ ନାହିଁ ।
(4) ମାନକ ବିଚ୍ୟୁତି (Standard deviation) – କୌଣସି ବିତରଣ ସାରଣୀରେ ମାଧ୍ୟମାନ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ବର୍ଗର ମାଧ୍ଯମାନର ଧନାତ୍ମକ ବର୍ଗମୂଳକୁ ମାନକ ବିଚ୍ୟୁତି କୁହାଯାଏ । ସାଧାରଣତଃ ଏହା ଓ (ସିଗ୍ମା) ଦ୍ଵାରା ସୂଚୀତ କରାଯାଏ । ଏହା ବିଭିନ୍ନ ପ୍ରଣାଳୀରେ ନିର୍ଣ୍ଣୟ କରିହୁଏ । ସୁତରାଂ;
SD Or \(\sigma=\sqrt{\frac{\Sigma d x^2}{n}}\)
ଏବଂ ମାନକ ବିଚ୍ୟୁତିର ଗୁଣାଙ୍କ (Co-efficient of SD) = \(\frac{\delta}{x}\)
ମାନକ ବିଚ୍ୟୁତି ବିଚ୍ଛୁରଣ ପରିମାପକମାନଙ୍କ ମଧ୍ୟରେ ଅଧୂକ ଲୋକପ୍ରିୟ ପରିମାପକ ଅଟେ । ଏହା ବିତରଣର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ, ଅସ୍ପଷ୍ଟ ନୁହେଁ ଏବଂ ଏହା ଗାଣିତିକ ପ୍ରକ୍ରିୟାରେ ପୁନଃ ବ୍ୟବହୃତ ହୋଇଥାଏ । କିନ୍ତୁ ଏହା ନିର୍ଣ୍ଣୟ କରିବା ଓ ହୃଦୟଙ୍ଗମ କରିବା ଏତେ ସହଜ ନୁହେଁ ।
![]()
(5) ବିତରଣ ଗୁଣାଙ୍କ (Co-efficient of Variation) – ମାନକ ବିଚ୍ୟୁତି ଓ ମାଧ୍ଯମାନର ଶତକଡ଼ା ଅନୁପାତ କୁ ବିତରଣ ଗୁଣାଙ୍କ କୁହାଯାଏ । ସୁତରାଂ,
ବିଚରଣ ଗୁଣାଙ୍କ (c.v.) = \(\frac{\delta}{x} \times 100\)
ବିଚରଣ ଗୁଣାଙ୍କ ବଣ୍ଟନଗୁଡ଼ିକର ତୁଳନାତ୍ମକ ଅନୁଶୀଳନରେ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ କାର୍ଯ୍ୟ ନିର୍ବାହ କରିଥାଏ ।
(6) ଲରେଞ୍ଜ୍ ବକ୍ର (Lorenz curve) – ଲରେଞ୍ଜ ବକ୍ର ଏକ ଜ୍ୟାମିତିକ ବକ୍ର । ଏହା ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ମାପକ ହିସାବରେ ଗ୍ରହଣ କରାଯାଏ । 1905 ରେ ମ୍ୟାକ୍ସ ଓ ଲରେଞ୍ଜ୍ ଏହି ବକ୍ରକୁ ବ୍ୟବହାର କରି ଲୋକମାନଙ୍କର ସମ୍ପତ୍ତି ବଣ୍ଟନରେ ଥିବା ଅସମତାକୁ ପ୍ରଦର୍ଶନ କରିଥିବାରୁ ଏହାକୁ Lorenz curve ବା ଲରେଞ୍ଜ୍ ବଜ୍ର କୁହାଯାଏ । ରାଶିକୃତ ଚଳର ଲବ୍ଧାଙ୍କ ଶତାଂଶ ଓ ରାଶିକୃତ ବାରମ୍ବାରତାର ଶତାଂଶଗୁଡ଼ିକୁ ନେଇ ବିନ୍ଦୁମାନ ସ୍ଥାପନ କରି ସେଗୁଡ଼ିକୁ ଯୋଗ କଲେ ଲରେଞ୍ଜ୍ ବଜ୍ର ମିଳିଥାଏ । ଏହି ବକ୍ର ସମବଣ୍ଟନ (Line of equal distribution) ଠାରୁ ଅଧିକ ଦୂରରେ ରହିଲେ ବଣ୍ଟନରେ ଅସମତା ଅଧିକ ବୋଲି ଜାଣିବାକୁ ହେବ ।
୩। ବିସ୍ତାର କାହାକୁ କୁହାଯାଏ ? ବିଚ୍ଛୁରଣର ପରିମାପକ ଭାବରେ ଏହାର ସୁଗୁଣ ଓ ଦୁର୍ଗୁଣ ସହ ଏହାର ଉପଯୋଗିତା ବର୍ଣ୍ଣନା କର ।
Answer:
ଗୋଟିଏ ବିତରଣରେ ବୃହତ୍ତମ ଲବ୍ଧାଙ୍କ ଓ କ୍ଷୁଦ୍ରତମ ଲବ୍ଧାଙ୍କର ଅନ୍ତରର ପ୍ରକ୍ରିୟାକୁ ବିସ୍ତାର (Range) କୁହାଯାଏ । ବିଚ୍ଛୁରଣ ଏହା ସର୍ବାପେକ୍ଷା ସହଜ, ସରଳ ଓ ସ୍ଥୂଳ ପରିମାପ ଅଟେ । ପର୍ଯ୍ୟବେକ୍ଷଣର ଦୁଇ ଚୂଡ଼ାନ୍ତ ମୂଲ୍ୟରୁ ବିସ୍ତାର ନିର୍ଦ୍ଧାରଣ କରାଯାଏ । ଅର୍ଥାତ୍ ବିତରଣ ମାଳାର ସର୍ବାଧିକ ଓ ସର୍ବନିମ୍ନ ଲବ୍ଧାଙ୍କର ଅନ୍ତରଫଳରୁ ବିସ୍ତାର ଜଣାପଡ଼େ ।
ବିସ୍ତାର (Range) = ସର୍ବାଧିକ ମୂଲ୍ୟ (L) – ସର୍ବନିମ୍ନ ମୂଲ୍ୟ (S)
→R = L – S
ଏହା ବିସ୍ତାରର ବିଶୁଦ୍ଧ ପରିମାପକ ଅଟେ । ତେଣୁ ଏହା ତୁଳନାତ୍ମକ ଭାବରେ ବ୍ୟବହାର ହୋଇପାରେ ନାହିଁ । ଏହାର ଆପେକ୍ଷିକ ପରିମାପ ନିମନ୍ତେ ବିସ୍ତାରର ଗୁଣାଙ୍କ (Co-efficient of Range) ଅଧ୍ୟୟନ କରିବାକୁ ପଡ଼ିଥାଏ । ବିତରଣ ମାଳାର ସର୍ବାଧିକ ମୂଲ୍ୟ ଓ ସର୍ବନିମ୍ନ ମୂଲ୍ୟର ବିୟୋଗ ଓ ଯୋଗର ଅନୁପାତକୁ ବିସ୍ତାରର ଗୁଣାଙ୍କ କୁହାଯାଏ;
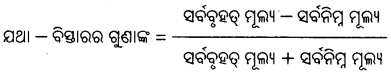
→ C.R= \(\frac{L-S}{L+S}\)
ସୁଗୁଣ (Merits) – ବିଚ୍ଛୁରଣର ପରିମାପକ ଭାବରେ ବିସ୍ତାରର ଅନେକଗୁଡ଼ିଏ ସୁଗୁଣ ରହିଛି ଯାହା ନିମ୍ନରେ ବର୍ଣ୍ଣନା କରାଗଲା ।
- ବିଚ୍ଛୁରଣ ପରିମାପକ ଭାବରେ ଏହା ସର୍ବାପେକ୍ଷା ସରଳ, ସହଜ ପଦ୍ଧତି ଅଟେ । ଏହାର ଗଣନା ମଧ୍ୟ ଖୁବ୍ ସହଜ ଓ ସରଳ ।
- ବିଚ୍ଛୁରଣର ବିଶୁଦ୍ଧ ପରିମାପକ ଆକାରରେ ଏହା ସ୍ଥୂଳ ମୂଲ୍ୟ ପ୍ରଦାନ କରୁଥିଲେ ହେଁ ଏହା ତ୍ୱରିତ୍ ଫଳ ପ୍ରଦାନ କରିଥାଏ । ଖୁବ୍ ସ୍ୱଳ୍ପ ସମୟ ମଧ୍ୟରେ ଏହା ଉତ୍ତର ନିରୂପଣ କରିଥାଏ ।
- ଉତ୍ପାଦନର ଗୁଣାତ୍ମକ ନିୟନ୍ତ୍ରଣ ପରିପ୍ରେକ୍ଷୀରେ ପରିସଂଖ୍ୟାନ ମାଳାରେ ଏହାର ବ୍ୟାପକ ପ୍ରୟୋଗ କରାଯାଇଥାଏ ।
- ଏହା ଗଣନା ପଦ୍ଧତି ଅତି ସହଜ ହୋଇଥବାରୁ ଜଣେ ସାଧାରଣ ବ୍ୟକ୍ତି ଏହାକୁ ସହଜରେ ବ୍ୟବହାର କରିପାରିଥାନ୍ତି । ତଥ୍ୟାବଳୀର ଏହା ଏକ ବ୍ୟାପକ ଆଲେଖ୍ୟ ପ୍ରତିପାଦନ କରେ ଯାହାର ସୀମା ମଧ୍ୟରେ ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଦୃଷ୍ଟିଗୋଚର ହୋଇଥାଏ ।
- ତଥ୍ୟାବଳୀର ଏହା ଏକ ବ୍ୟାପକ ଆଲେଖ୍ୟ ପ୍ରତିପାଦନ କରେ ଯାହାର ସୀମା ମଧ୍ୟରେ ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଦୃଷ୍ଟିଗୋଚର ହୋଇଥାଏ ।
ଦୁର୍ଗୁଣ (Demerits) –
ବିସ୍ତାରର ଗଣନା ପଦ୍ଧତି ସହଜ ଓ ସରଳ ହୋଇଥିଲେ ହେଁ ନିମ୍ନଲିଖିତ ଦୁର୍ଗୁଣ ଯୋଗୁଁ ଏହା ଏକ ଉତ୍ତମ ନିର୍ଭରଯୋଗ୍ୟ ପରିମାପକ ଭାବରେ ଗ୍ରହଣୀୟ ନୁହେଁ ।
- ଏହା ଚୂଡ଼ାନ୍ତ ଲବ୍ଧାଙ୍କ ଦ୍ୱାରା ପ୍ରଭାବିତ ହୋଇଥାଏ । କାରଣ ଏହି ପଦ୍ଧତି ବିତରଣ ମାଳାର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ ହୋଇ ନଥାଏ । ତେଣୁ ଏହାକୁ ଏକ ନିର୍ଭରଯୋଗ୍ୟ ପରିମାପକ ଭାବରେ ଗ୍ରହଣ କରାଯାଏ ନାହିଁ ।
- ବିସ୍ତାର କେବଳ ସର୍ବାଧିକ ଲବ୍ଧାଙ୍କ ଓ ସର୍ବନିମ୍ନ ଲବ୍ଧାଙ୍କ ଦ୍ବାରା ନିର୍ଦ୍ଧାରିତ ହୋଇଥାଏ । ତେଣୁ ଏହା ଅନ୍ୟ ଲବ୍ଧାଙ୍କର ବିଚ୍ଛୁରଣ ମାପ କରିପାରେ ନାହିଁ ।
- ନମୁନାର ପରିବର୍ତ୍ତନଦ୍ୱାରା ବିସ୍ତାର ବିଶେଷଭାବେ ପ୍ରଭାବିତ ହୋଇଥାଏ ।
- ଅବାଧ ସଂଭାଗଯୁକ୍ତ ବାରମ୍ବାରତା ବିତରଣର ବିସ୍ତାର ନିର୍ଣ୍ଣୟ ସମ୍ଭବ ନୁହେଁ ।
![]()
ବିସ୍ତାରର ଉପଯୋଗିତା – ବିସ୍ତାର ଦୁର୍ଗୁଣ ରହିଥିଲେ ସୁଦ୍ଧା ଏହା ଅନେକ କ୍ଷେତ୍ରରେ ଉପଯୋଗୀ ସାବ୍ୟସ୍ତ ହୋଇଥାଏ ।
- ଗୁଣାତ୍ମକ ମାନ ନିୟନ୍ତ୍ରଣ – ଗୁଣାତ୍ମକ ମାନ ନିୟନ୍ତ୍ରଣ କ୍ଷେତ୍ରରେ ବିସ୍ତାରର ସ୍ଵତନ୍ତ୍ର ପ୍ରୟୋଗ କରାଯାଇଥାଏ । କଳକାରଖାନାରେ ଉତ୍ପାଦିତ ପୂର୍ବ ଦ୍ରବ୍ୟଗୁଡ଼ିକର ଗୁଣାତ୍ମକ ମାନ ପରିବର୍ତ୍ତନର ଅଧ୍ୟୟନ ପାଇଁ ବିସ୍ତାରକୁ ବ୍ୟବହାର କରାଯାଏ । ବିସ୍ତାର ମାଧ୍ୟମରେ ନିୟନ୍ତ୍ରଣ ଚାର୍ଟ ପ୍ରସ୍ତୁତ କରାଯାଏ ।
- ପାଣିପାଗର ପ୍ରାକ୍ କଥନ – ଭବିଷ୍ୟତର ପାଣିପାଗ ସଂପର୍କରେ ଗଣନା ପାଇଁ ଏହା ବହୁଳ ଭାବରେ ବ୍ୟବହୃତ ହୋଇଥାଏ । ପାଣିପାଗର ସୀମା ତଥା ଉତ୍ତାପର ସ୍ତର ଜାଣିବାପାଇଁ ସାଧାରଣ ଲୋକ ବିଶେଷ ଆଗ୍ରହ ପ୍ରକାଶ କରିଥାନ୍ତି ।
- ପରିବର୍ତ୍ତନର ପରିମାପ – ତଥ୍ୟାବଳୀର ପରିବର୍ତ୍ତନ ଅଧ୍ୟୟନ ନିମିତ୍ତ ବିସ୍ତାରକୁ ବ୍ୟବହାର କରାଯାଏ । ରୋଗୀର ଶରୀରର ଉତ୍ତାପର ତାରତମ୍ୟ ବା ପରିବର୍ଭନ ସଂପର୍କରେ ଜାଣିବାପାଇଁ ଏହାର ପ୍ରୟୋଗ କରାଯାଇଥାଏ । ବଜାରରେ ଦାମ୍ର ପରିବର୍ତ୍ତନ ଓ ଅଂଶ ବଜାରରେ ପୁଞ୍ଜିର ଚାହିଦାର ପରିବର୍ତ୍ତନ ଇତ୍ୟାଦି ବିସ୍ତାରଦ୍ୱାରା ମାପ କରାଯାଇଥାଏ ।
୪। ମାଧ୍ୟ ବିଚ୍ୟୁତି (Mean Deviation) କ’ଣ ? ଏହି ପଦ୍ଧତି ରହିଥିବା ସୁଗୁଣ ଓ ଦୁର୍ଗୁଣ ସହ ଏହାର ଉପଯୋଗିତା ବର୍ଣ୍ଣନା କର ।
Answer:
କୌଣସି ବିତରଣ ସାରଣୀରେ ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ଓ ଲବ୍ଧାଙ୍କ ମାନଙ୍କ ମଧ୍ୟରେ ଅନ୍ତରର ପରମ ମାନର ମାଧ୍ଯମାନକୁ ମାଧ୍ୟ ବିଚ୍ୟୁତି (Mean Deviation) କୁହାଯାଏ । ଏହାକୁ ମଧ୍ୟ ହାରାହାରି ବିଚ୍ୟୁତି (Average deviation) କୁହାଯାଏ । କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତିର ଯେକୌଣସି ପରିମାପ; ଯଥା – ମାଧ୍ଯମାନ, ମଧ୍ୟମା, ଗରିଷ୍ଠକ ଦ୍ବାରା ପ୍ରସ୍ତୁତ ହେଉଥିବା କୌଣସି ମାଳାର ବିଚ୍ୟୁତିମାନଙ୍କର ଗାଣିତିକ ମାଧ୍ୟମାନକୁ ମାଧବିଚ୍ୟୁତି ବୋଲି କୁହାଯାଇଥାଏ ।
ବିତରଣ ମାଳାର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ ବିଚ୍ଛୁରଣ ପରିମାପକୁ ମାଧବିଚ୍ୟୁତି ବୋଲି କୁହାଯାଇଥାଏ । ଏହା M.D. ଭାବରେ ଚିହ୍ନିତ କରାଯାଏ । ମାଧ୍ୟବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କଲାବେଳେ କେବଳ ଧନାତ୍ମକ ଚିହ୍ନକୁ ଗୁରୁତ୍ଵ ଦିଆଯାଇଥାଏ । ଏ କ୍ଷେତ୍ରରେ ଋଣାତ୍ମକ ଚିହ୍ନ ମଧ୍ୟ ଧନାତ୍ମକ ଚିହ୍ନ ବୋଲି ଧରିନିଆଯାଏ । ତେଣୁ ଏହା ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ଓ ଲବ୍ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ପରମ ମାନର ମାଧ୍ଯମାନ ଅଟେ । ମାଧ୍ୟ ବିଚ୍ୟୁତିକୁ ପୂର୍ଣ୍ଣ ବା ନିରଙ୍କୁଶ ବା ବିଶୁଦ୍ଧ ବିଚ୍ୟୁତି ବୋଲି କୁହାଯାଏ ।
ନିଶ୍ଚୟ ପଦ୍ଧତି :
ମାଧ୍ୟ ବିଚ୍ୟୁତି (M.D) = \(\frac{\Sigma|D|}{N}=\frac{\Sigma|(X-\bar{X})|}{N}\)
ଏଠାରେ X ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ହୋଇପାରେ । N ଏଠାରେ ଲବ୍ଧାଙ୍କ ସଂଖ୍ୟା ସୂଚାଇଥାଏ । ଏହା ଏକ ବିଶିଷ୍ଟ ପରିମାପ ହୋଇଥିବାରୁ ବିଭିନ୍ନ ମାଳାର ଭିନ୍ନତା ତୁଳନା କରିବା ପାଇଁ ଆପେକ୍ଷିକ ମାଧ ବିଚ୍ୟୁତିର ଅବତାରଣା
ମାଧବିଚ୍ୟୁତିର ଗୁଣାଙ୍କ (Co-efficient of Mean Deviation) – ଆପେକ୍ଷିକ ମାଧ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କରିବାପାଇଁ କୌଣସି ତଥ୍ୟାବଳୀର ମାଧ ବିଚ୍ୟୁତିକୁ ସଂପୃକ୍ତ ହାରାହାରି ମୂଲ୍ୟ (Average value); ଯଥା ମାଧ୍ଯମାନ ବା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକଦ୍ୱାରା ଭାଗ କରାଯାଇଥାଏ । ଯଦି ବିଚ୍ୟୁତିଗୁଡ଼ିକ ମାଧମାନରୁ ନିର୍ଣ୍ଣୟ କରାଯାଇଥବ, ତା’ହେଲେ ମାଧ ବିଚ୍ୟୁତିକୁ ସେହି ମାଧ୍ଯମାନଦ୍ୱାରା ଭାଗ କରିବାକୁ ପଡ଼ିଥାଏ, ସେହିପରି ମଧ୍ଯମା ବା ଗରିଷ୍ଠକ ଦ୍ବାରା ନିର୍ଣ୍ଣୟ କରାଯାଇଥିଲେ ଏହା ମଧ୍ୟମା ବା ଗରିଷ୍ଠକ ଦ୍ବାରା ଭାଗ କରାଯାଇଥାଏ ।

ଏହାକୁ ଶତକଡ଼ାରେ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେଲେ ଉକ୍ତ ସୂତ୍ରରେ 100 ଗୁଣନ କରିବାକୁ ହୋଇଥାଏ ।
ମାଧ୍ୟବିଚ୍ଯୁତିର ସୁଗୁଣ (Merits) :
- ଏହି ପଦ୍ଧତି ସହଜ, ସରଳ ଓ ବୋଧଗମ୍ୟ ।
- ମାଧ୍ୟବିଚ୍ୟୁତି ଏକ ଗଣନାତ୍ମକ ମୂଲ୍ୟ ଅଟେ । ବିଭିନ୍ନ ପଦ୍ଧତିରେ ଗଣନା କରାଯାଇ ତାହାର ମୂଲ୍ୟ ସ୍ଥିର କରାଯାଇଥାଏ ।
- ଏହା ଅଧିକ ପ୍ରତିନିଧ୍ଵ କରିଥାଏ । ମାଧବିଚ୍ୟୁତି ପ୍ରତ୍ୟେକ ଲବ୍ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ ହୋଇଥାଏ ।
- ଚୂଡ଼ାନ୍ତ ଲବ୍ଧାଙ୍କଦ୍ୱାରା ପ୍ରଭାବିତ ହୋଇ ନଥାଏ ।
- ମାଧ୍ୟ ବିଚ୍ୟୁତି ଯେକୌଣସି ହାରାହାରି; ଯଥା – ମାଧ୍ଯମାନ, ମଧ୍ଯମା, ଗରିଷ୍ଠକରୁ ଗଣନା କରାଯାଇଥାଏ ।
![]()
ଦୁର୍ଗୁଣ (Demerits):
- ଗାଣିତିକ ବ୍ୟାଖ୍ୟା ନିମନ୍ତେ ଏହା ଅନୁପଯୁକ୍ତ କାରଣ ଏହା ଧନାତ୍ମକ ଓ ଋଣାତ୍ମକ ଚିହ୍ନକୁ ବିଚାରକୁ ନେଇ ନ ଥାଏ, ଯାହାଫଳରେ ଏହାର ଗାଣିତିକ ବ୍ୟାଖ୍ୟା ଅପ୍ରାସଙ୍ଗିକ ହୋଇଥାଏ ।
- ମାଧ୍ୟବି ବ୍ୟତିର ବିଚ୍ଛୁରଣର ସଠିକ ପରିମାପକ ନୁହେଁ । ବିଶେଷକରି ଗରିଷ୍ଠକରୁ ପ୍ରସ୍ତୁତ ମାଧବିଚ୍ୟୁତି ବିଶେଷ ତ୍ରୁଟିପୂର୍ଣ୍ଣ ଓ ଅବିଶ୍ୱସନୀୟ ।
- ମାଧ୍ୟବିଚ୍ୟୁତି ଯେକୌଣସି ହାରାହାରି ଦ୍ବାରା ନିର୍ଦ୍ଧାରିତ ହେଉଥିବାରୁ ଏହା ଉପଯୁକ୍ତ ପରିମାପକ ଭାବରେ ବିବେଚନା କରାଯାଇ ନ ଥାଏ ।
- ମାଧ୍ୟବିଚ୍ୟୁତିର ବ୍ୟବହାର ବ୍ୟାପକ ନୁହେଁ ।
ଉପଯୋଗିତା – ଗାଣିତିକ ଦୋଷତ୍ରୁଟି ପରିଲକ୍ଷିତ ହେଉଥିଲେହେଁ ଏହା ଏକ ସରଳ ପଦ୍ଧତି ଯୋଗୁଁ ଗ୍ରହଣୀୟ ହୋଇଥାଏ । କ୍ଷୁଦ୍ର ନମୁନା ସଂଗ୍ରହରେ ଏହାର ଉପଯୋଗିତା ଅଧ୍ଵ । ଅର୍ଥନୈତିକ, ସାମାଜିକ ଓ ବ୍ୟବସାୟିକ ବ୍ୟାପାରରେ ଏହା ବିଶେଷ ବ୍ୟବହାର ହୋଇଥାଏ । ବଜାର ସମସ୍ୟାରେ ଏହାର ଉପଯୋଗିତା ଦୃଷ୍ଟିଗୋଚର ହୋଇଥାଏ । ବ୍ୟବସାୟିକ ଉତ୍ଥାନ ପତନର ଗଣନାରେ ଏହା ବିଶେଷ ଉପଯୋଗୀ ।
୫। ମାନକ ବିଚ୍ୟୁତି କାହାକୁ କୁହାଯାଏ ? ଏହାର ସୁଗୁଣ ଓ ଦୁର୍ଗୁଣ ବର୍ଣ୍ଣନା କର ।
Answer:
କୌଣସି ବିତରଣ ସାରଣୀରେ ମାଧ୍ୟମାନ ଓ ଲବ୍ଧାଙ୍କ ମାନଙ୍କର ଅନ୍ତରର ବର୍ଗର ମାଧ୍ଯମାନର ଧନାତ୍ମକ ବର୍ଗମୂଳକୁ ମାନକ ବିଚ୍ୟୁତି (Standard deviation) କୁହାଯାଏ । ମାନକ ବିଚ୍ୟୁତିକୁ ବର୍ଗମୂଳ ମାଧମାନ ବର୍ଗ ବିଚ୍ୟୁତି ମଧ୍ୟ କୁହାଯାଏ । ‘ଓ” ଦ୍ୱାରା ଚିହ୍ନିତ ଏହି ପରିମାପ ବିଚ୍ଛୁରଣର ସମସ୍ତ ପରିମାପକ ଠାରୁ ଅଧିକ ଗ୍ରହଣଯୋଗ୍ୟ । ମାନକ ବିଚ୍ୟୁତିଦ୍ୱାରା ମାଧ୍ଯମାନ ଚତୁଃପାର୍ଶ୍ବରେ ଲବ୍ଧାଙ୍କମାନଙ୍କର ବ୍ୟାପ୍ତି ବା ବିସ୍ତୃତିର ପରିସର କଳ୍ପନା କରାଯାଇଥାଏ ।
ନିର୍ଦ୍ଧାରଣ ପଦ୍ଧତି – ମାନକ ବିଚ୍ୟୁତି \((\sigma)=\sqrt{\frac{\Sigma(\mathrm{X}-\overline{\mathrm{X}})^2}{\mathrm{~N}}}\)
କିମ୍ବା ମାଧ୍ଯମାନ ଏକ ଦଶମିକ ସଂଖ୍ୟା ହୋଇଥିଲେ
ମାନକ ବିଚ୍ୟୁତି \((\sigma)=\sqrt{\frac{\Sigma x}{N}-\frac{\Sigma x^2}{N}}\)
ବୈଶିଷ୍ଟ୍ୟ –
- ଗାଣିତିକ ମାଧ୍ୟମାନରୁ ଏହାର ନିମ୍ନମୂଲ୍ୟ ନିର୍ଦ୍ଧାରିତ ହୁଏ ।
- ମାଧ୍ୟମାନରୁ ମିଳୁଥିବା ବିଚ୍ୟୁତିର ମୂଲ୍ୟରୁ ଧନାତ୍ମକ (+) ଓ ଋଣାତ୍ମକ (–) ଚିହ୍ନକୁ ବିଚାର କରାଯାଏ ନାହିଁ ।
- ବିଚ୍ୟୁତି ବର୍ଗର ଗାଣିତିକ ମାଧ୍ଯମାନର ବର୍ଗମୂଳ ଗଣନା କରିବାକୁ ହୁଏ । ଯାହା ଫଳ ନିର୍ଦ୍ଧାରଣ ମାନକ ବିଚ୍ୟୁତି ଅଟେ ।
ମାନକ ବିଚ୍ୟୁତିର ଗୁଣାଙ୍କ (Co-efficient of standard deviation) :
ଦୁଇଟି ରାଶିମାଳାର ମାନକ ବିଚ୍ୟୁତିର ବିଭିନ୍ନତାର ଆପେକ୍ଷିକ ପରିମାପ ସ୍ଥିର କରିବାପାଇଁ ମାନକ ବିଚ୍ୟୁତିର ଗୁଣାଙ୍କ ବ୍ୟବହାର କରାଯାଇଥାଏ ।
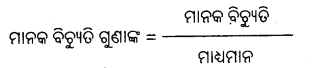
ମାନକ ବିଚ୍ୟୁତିର ସୁଗୁଣ (Merits) :
- ମାନକ ବିଚ୍ୟୁତି ନିର୍ଦ୍ଦିଷ୍ଟ ଓ ଉତ୍ତମ ପରିମାପକ ରୂପେ ବିଶେଷ ଭାବରେ ଗ୍ରହଣୀୟ । ବିଚ୍ଛୁରଣର ଏହା ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାପକ । ପ୍ରତ୍ୟେକ ଅବସ୍ଥାରେ ଏହି ପରିମାପ ସମ୍ଭବ ହୋଇଥାଏ ।
- ତଥ୍ୟାବଳୀର ସମସ୍ତ ଲବ୍ଧାଙ୍କ ଉପରେ ଏହା ପର୍ଯ୍ୟବସିତ ତେଣୁ ଏହା ଅଧ୍ବକ ପ୍ରତିନିଧ୍ୟ କରିଥାଏ ।
- ବିଚ୍ଛୁରଣ ମାପର ଏହା ସ୍ପଷ୍ଟ ଓ ନିର୍ଦ୍ଦିଷ୍ଟ ଚିତ୍ର ପ୍ରଦାନ କରେ । ଦୁଇ ବା ତତୋଽଧ୍ଵ ତଥ୍ୟାବଳୀର ବିଭିନ୍ନତା ତୁଳନା କରିବାପାଇଁ ମାନକ ବିଦ୍ୟୁତିର ଆପେକ୍ଷିକ ପରିମାପ; ଯଥା – ବିତରଣ ଗୁଣାଙ୍କ, ପାରସ୍ପରିକ ସବନ୍ଧ, ନମୁନା ଓ ପରିସଂଖ୍ୟାନ ସିଦ୍ଧାନ୍ତ ପ୍ରସ୍ତୁତିପାଇଁ ଭିତ୍ତି ସ୍ଥାପନ କରେ ।
- ନମୁନା । ପରିବର୍ତ୍ତନରେ ମାନକ ବିଚ୍ୟୁତି ବିଶେଷ ପ୍ରଭାବିତ ହୋଇ ନଥାଏ । କାରଣ ନମୁନାର ସମସ୍ତ ମୂଲ୍ୟଦ୍ୱାରା ଏହା ନିର୍ଦ୍ଧାରିତ ହୋଇଥାଏ ।
- ମାନକ ବିଚ୍ୟୁତି ସଠିକ ଗାଣିତିକ ପ୍ରଦାନ କରିବା ସହିତ ଅଧିକ ବୀଜଗାଣିତିକ ପ୍ରତିପାଦନ ପାଇଁ ସକ୍ଷମ ହୋଇଥାଏ । ଏହା ଧନାତ୍ମକ ଓ ଋଣାତ୍ମକ ଚିହ୍ନକୁ ବାଦ୍ ଦେଇ ନ ଥାଏ ।
![]()
ଦୁର୍ଗୁଣ (Demerits):
- ଅନେକ ଗାଣିତିକ ପ୍ରକ୍ରିୟା ସହ ଜଡ଼ିତ ଥିବାରୁ ଏହାର ଗଣନା ଅପେକ୍ଷାକୃତ କଷ୍ଟସାଧ୍ୟ । ସାଧାରଣ ଲୋକଙ୍କ ପାଇଁ ଏହା ବୋଧଗମ୍ୟ ନୁହେଁ ।
- ମାନକ ବିଚ୍ୟୁତି କ୍ଷେତ୍ରରେ ଚୂଡ଼ାନ୍ତ ମୂଲ୍ୟକୁ ଅଧିକ ଗୁରୁତ୍ୱ ଦିଆଯାଇଥାଏ । କାରଣ ଏହାର ମୂଲ୍ୟର ବର୍ଗ ବାହାର କରାଯାଏ ।
- ମାନକ ବିଚ୍ୟୁତିର ପରିସର ସୀମିତ ।
- ବିଭିନ୍ନତା ପରିମାପର ଏହା ବିଶୁଦ୍ଧ ପରିମାପ ହୋଇଥିବାରୁ ଏହା ଆପେକ୍ଷିକ ପରିମାପ କରିପାରେ ନାହିଁ । ଦୁଇରୁ ଅଧିକ ବିତରଣ ମାଳାର ତୁଳନା ପାଇଁ ଏହା ବ୍ୟବହୃତ ହୋଇ ନ ଥାଏ ।
ଉପରୋକ୍ତ ଦୁର୍ଗୁଣ ସତ୍ତ୍ବେ, ମାନକ ବିଚ୍ୟୁତି ଏକ ଉତ୍ତମ ପରିମାପକ ଭାବରେ ଆଦୃତ ହୋଇଛି । ବିଚ୍ଛୁରଣର ପରିମାପକ ଭାବରେ ଏହା ସର୍ବୋତ୍କୃଷ୍ଟ ଅଟେ । ଅନ୍ୟାନ୍ୟ ପରିମାପକ ଠାରୁ ଏହି ପଦ୍ଧତି ବିଶେଷ ଉପଯୋଗୀ ।
