CHSE Odisha Class 11 Economics Solutions Chapter 21 ସହସମ୍ବନ୍ଧ ଓ ସମାଶ୍ରୟଣ

Odisha State Board CHSE Odisha Class 11 Economics Solutions Chapter 21 ସହସମ୍ବନ୍ଧ ଓ ସମାଶ୍ରୟଣ Questions and Answers.

CHSE Odisha 11th Class Economics Solutions Chapter 21 ସହସମ୍ବନ୍ଧ ଓ ସମାଶ୍ରୟଣ

ବସ୍ତୁନିଷ୍ଠ ଓ ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନରେ ପ୍ରଦତ୍ତ ବିକଳ୍ପଉତ୍ତରମାନଙ୍କ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ।

୧। ଯଦି ଦୁଇଟି ବିଚ୍ୟୁତି ଏକ ଦିଗରେ ସଂଗଠିତ ହେଉଥାଏ, ତେବେ ସେମାନଙ୍କର ସହ ସମ୍ବନ୍ଧ
(i) ଧନାତ୍ମକ
(ii) ରଣାତ୍ମକ
(iii) ଶୂନ୍ଯ
(iv) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(i) ଧନାତ୍ମକ

୨। ଯଦି ଦୁଇଟି ଚଳର ବିଚ୍ୟୁତି ବିପରୀତ ଦିଗରେ ସଂଘଟିତ ହେଉଥାଏ, ତେବେ ସେମାନଙ୍କ ମଧ୍ୟରେ
(i) ଅନୁଲୋମ ସମ୍ପର୍କ ଥାଏ
(ii) ପ୍ରତିଲୋମ ସମ୍ପର୍କ ଥାଏ
(iii) ସମ୍ପର୍କ ନ ଥାଏ
(iv) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(ii) ପ୍ରତିଲୋମ ସମ୍ପର୍କ ଥାଏ

୩। ତିନି ବା ତଦୁର୍ଦ୍ଧ୍ବ ଚଳମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ସହ ସମ୍ବନ୍ଧକୁ କ’ଣ କୁହାଯାଏ ?
(i) ସରଳ ସହ-ସମ୍ବନ୍ଧ
(ii) ଏକାଧିକ ସହ-ସମ୍ବନ୍ଧ
(iii) ଆଂଶିକ ସହ-ସମ୍ବନ୍ଧ
(iv) ସ୍ଥିତି ସମ୍ବନ୍ଧ
Answer:
(ii) ଏକାଧିକ ସହ-ସମ୍ବନ୍ଧ

୪। ଗୋଟିଏ ଚଳର ଏକକ ପରିବର୍ତ୍ତନ ଯୋଗୁଁ ଅନ୍ୟ ଏକ ଚଳର ଧ୍ରୁବକ (ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଏକକ) ପରିବର୍ତ୍ତନ ଘଟୁଥୁଲେ
(i) ସରଳ ରେଖକ
(ii) ବକ୍ର ରିଖକ
(iii) ଏକ୍ସପୋନେସିଆଲ
(iv) ଲଗାରିଦମିକ
Answer:
(i) ସରଳରେଖକ

୫। ଦୁଇଟି ଚଳର ପରିବର୍ତ୍ତନ ପ୍ରାୟ ସମାନ ଅନୁପାତରେ ଘଟୁଥିଲେ ସେମାନଙ୍କର ସହ-ସମ୍ବନ୍ଧ
(i) ଉଚ୍ଚ
(ii) ନିମ୍ନ
(iii) ଶୂନ୍ଯ
(iv) ପୂର୍ଣ୍ଣ
Answer:
(i) ଉଚ୍ଚ

୬। କାର୍ଲପିଅରସନ୍‌ଙ୍କ ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର (r) ସଂଜ୍ଞା
(i) Cov (X,Y)/σx
(ii) Cov(x,y)/σy
(iii) Cov (x,y)/σx.σy (iv)
(iv) \(\frac{V .(x) V(y)}{\sigma x . \sigma y}\)
Answer:
(iii) Cov (x,y)/σx.σy

୭। n ଯଦି ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ ହୁଏ, ତେବେ
(i) n>1
(ii) n<-1
(iii) -1≤1≤1
(iv) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(iii) -1≤1≤1

୮। ଯଦି n = 1 ହୁଏ ତେବେ
(i) ସହସମ୍ବନ୍ଧ ପୂର୍ଣ ହୋଇଥାଏ
(ii) ସହସମ୍ବନ୍ଧ ଧନାତ୍ମକ ହୋଇଥାଏ
(iii) ସହସମ୍ବନ୍ଧ ଋଣାତ୍ମକ ହୋଇଥାଏ
(iv) ସହସମ୍ବନ୍ଧ ପୂର୍ଣ୍ଣ ଓ ଧନାତ୍ମକ ହୋଇଥାଏ
Answer:
(iv) ସହସମ୍ବନ୍ଧ ପୂର୍ଣ୍ଣ ଓ ଧନାତ୍ମକ ହୋଇଥାଏ

୯। ଯଦି  Σ(x – x̄)²=4, Σ(y – ȳ)² =9 ଏବଂ Σ(x – x̄)² (y – ȳ)=5 ହୁଏ, ତେବେ ସହସମ୍ବନ୍ଧ (r)
(i) \(\frac{5}{6}\)
(ii) \(\frac{6}{5}\)
(iii) \(\frac{5}{36}\)
(iv) \(\frac{6}{35}\)
Answer:
\(\frac{5}{6}\left[r=\frac{\sum(X-\bar{X})(Y-\bar{Y})}{\sqrt{(X-\bar{X})^2(Y-\bar{Y})^2}}=\frac{5}{\sqrt{4 \times 9}}=\frac{5}{2 \times 3}=\frac{5}{6}\right]\)

୧୦। ଯଦି r = 0.6 6x=2 ଏବଂ 6y=5 ହୁଏ ତେବେ Cov(x.y)
(i) 4
(ii) 5
(iii) 6
(iv) 7
Answer:
(iii) 6

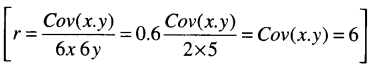
୧୧। ସମାଶ୍ରୟଣ କେଉଁ ଉକ୍ତିକୁ ପ୍ରତିପାଦିତ କରିଥାଏ ?
(i) କାରଣ ଓ ପ୍ରଭାବ ସମ୍ପର୍କ
(ii) ଭବିଷ୍ୟତ କଳନା
(iii) ସମ୍ପର୍କର ଦିଗ ଓ ପ୍ରବଣତା
(iv) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(iv) ଉପରୋକ୍ତ ସମସ୍ତ

୧୨। ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟିକୁ ସମାଶ୍ରୟଣ ପ୍ରତିପାଦିତ କରିଥାଏ ?
(i) ଭବିଷ୍ୟତ କଥନ
(ii) ସମ୍ପର୍କର ଆକଳନ
(iii) ସହ ସମ୍ପର୍କ
(iv) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(iv) ଉପରୋକ୍ତ ସମସ୍ତ

୧୩ । ସମାଶ୍ରୟଣ ସମୀକରଣ y = a + bx ହେଉଛି-
(i) ସ୍ଵତନ୍ତ୍ର ଚଳ
(ii) ନିର୍ଭରଶୀଳ ଚଳ
(iii) ଅନିୟମିତ ଚଳ
(iv) ସ୍ଵାଧୀନ ଚଳ
Answer:
(iv) ସ୍ଵାଧୀନ ଚଳ

୧୪ । ସମାଶ୍ରୟଣ ସମୀକରଣ y = a + bx ହେଉଛି –
(i) ସ୍ଵାଧୀନ ଚଳ
(ii) ନିର୍ଭରଶୀଳ ଚଳ
(iii) ଅନିୟମିତ ଚଳ
(iv) ସ୍ଵତନ୍ତ୍ର ଚଳ
Answer:
(ii) ନିର୍ଭରଶୀଳ ଚଳ

B. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :

୧। ଦୁଇଟି ଚଳ ଏକ ଦିଗରେ ପରିବର୍ତ୍ତିତ ହେଉଥଲେ ସେମାନଙ୍କର ସହସମ୍ବନ୍ଧ _____________________ ହୋଇଥାଏ।
Answer:
ଧନାତ୍ମକ

୨। ଦୁଇଟି ଚଳର ସହସମ୍ବନ୍ଧ ଋଣାତ୍ମକ ହୋଇଥିଲେ ସେମାନଙ୍କର ପରିବର୍ତ୍ତନ __________________ ଦିଗରେ ସଂଘଟିତ ହୋଇଥାଏ ।
Answer:
ବିପରୀତ

୩। ସରଳରେଖକ ସହସମ୍ବନ୍ଧ ଥିଲେ, ଗୋଟିଏ ଚଳର ଏକକ ପରିବର୍ତ୍ତନ ପାଇଁ ଅନ୍ୟ ଚଳର ଏକ ________________ ହୋଇଥାଏ।
Answer:
ଧ୍ରୁବକ

୪। X ଓ Y ଚଳ ଦ୍ଵୟର ସହସମ୍ବନ୍ଧ ବକ୍ରରେଖକ ହୋଇଥିଲେ _____________________ ଏକ ଧ୍ରୁବକ ରାଶି ହୋଇ ନ ଥାଏ ।
Answer:
\(\frac{\Delta Y}{\Delta X}\)

୫। ଅନେକ ଚଳରାଶି ପରସ୍ପର ସମ୍ପର୍କିତ ହୋଇଥିଲେ, କୌଣସି ଦୁଇ ଚଳରାଶି ଉପରୁ ଅନ୍ୟ ଚଳରାଶିମାନଙ୍କର ପ୍ରଭାବ ଅପସାରଣ କଲାପରେ ସେମାନଙ୍କ ମଧ୍ୟରେ ଯେଉଁ ସହସମ୍ବନ୍ଧ ପରିଲକ୍ଷିତ ହୁଏ, ତାହାକୁ _____________________ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।
Answer:
ଆଂଶିକ

୬। ଦୁଇଟି ଚଳ ସମାନ ଅନୁପାତରେ ପରିବର୍ତ୍ତନ ହେଉଥିଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ ________________________ ସହସମ୍ବନ୍ଧ ପରିଲକ୍ଷିତ ହୁଏ।
Answer:
ପୂର୍ଣଓ

୭। ସହସମ୍ୱନ୍ଧ ଗୁଣାଙ୍କ ________________ ଠାରୁ ବୃହତ୍ତର ନୁହେଁ ।
Answer:
+୧

୮। ସହସମ୍ୱନ୍ଧ ଗୁଣାଙ୍କ ________________ ଠାରୁ ବୃହତ୍ତର ନୁହେଁ ।
Answer:
-୧

୯। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ ଅରିଜିନ ଓ ସ୍କେଲର ପରିବର୍ତ୍ତନର _____________________ ଅଗେ ।
Answer:
ନିରପେକ୍ଷ

୧୦। n = 0 ହେଲେ ଚଳମାନଙ୍କ ମଧ୍ୟରେ ________________________ ନାହିଁ ବୋଲି କୁହାଯାଏ ।
Answer:
ସହସମ୍ବନ୍ଧ

୧୧। ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ହାରାହାରି ସମ୍ପର୍କକୁ ___________________ କୁହାଯାଏ ।
Answer:
ସମାଶ୍ରୟଣ

୧୨। ସମାଶ୍ରୟଣକୁ ବୁଝାଉଥବା ରେଖାଚିତ୍ରକୁ _________________ କୁହାଯାଏ ।
Answer:
ସମାଶ୍ରୟଣ ରେଖା

୧୩। ଯେଉଁ ଚଳର ଭବିଷ୍ୟତ କଥନ କରାଯାଏ, ତାହାକୁ ______________________ କୁହାଯାଏ ।
Answer:
ସ୍ଵାଧୀନ ଚଳ

୧୪। ସମାଶ୍ରୟଣ ସମୀକରଣଟି _____________________ ରୂପେ ଲେଖାଯାଏ ।
Answer:
y = a + bx |

C. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।

୧। ଦୁଇଟି ଚଳ ସମଦିଗରେ ଗତି କଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ କେଉଁ କିସମର ସହସମ୍ବନ୍ଧ ରହିଥାଏ ?
Answer:
ଦୁଇଟି ଚଳ ସମଦିଗରେ ଗତିକଲେ ସେମାନ ମଧ୍ୟରେ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ରହିଥାଏ।

୨। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ କେତେ ହୋଇପାରେ ?
Answer:
ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ –୧ରୁ +୧ ମଧ୍ୟରେ ହୋଇପାରେ।

୩। ସହସମ୍ବନ୍ଧର ସର୍ବାଧ‌ିକ ମୂଲ୍ୟ କେତେ ହୋଇପାରେ ?
Answer:
ସହସମ୍ବନ୍ଧର ସର୍ବାଧ‌ିକ ମୂଲ୍ୟ +୧ ହୋଇପାରେ।

୪। ଦୁଇଟି ଚଳ ବିପରୀତ ଦିଗରେ ଗତି କଲେ, ସେମାନଙ୍କ ମଧ୍ୟରେ କେଉଁ କିସମର ସହସମ୍ବନ୍ଧ ଦେଖାଯାଏ ?
Answer:
ଦୁଇଟି ଚଳ ବିପରୀତ ଦିଗରେ ଗତିକଲେ, ସେମାନଙ୍କ ମଧ୍ୟରେ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ ଦେଖାଯାଏ।

୫। ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ସମାନୁପାତିକ ପରିବର୍ତ୍ତନ ଦେଖାଦେଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ କେଉଁ କିସମର ସହସମ୍ବନ୍ଧ ଥାଏ ?
Answer:
ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ସମାନୁପାତିକ ପରିବର୍ତ୍ତନ ଦେଖାଦେଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ ସମ୍ପୂର୍ଣ ସହ ସମ୍ବନ୍ଧ ଥାଏ।

୬। ସହସମ୍ବନ୍ଧ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଦୁଇଟି ରାଶି ମଧ୍ୟରେ ରହିଥିବା ପାରସ୍ପରିକ ସମ୍ପର୍କକୁ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

୭। ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ କ’ଣ ?
Answer:
ଯେତେବେଳେ ଦୁଇଟି ରାଶିର ପରିବର୍ତ୍ତନ ସମଦିଗରେ ସଂଗଠିତ ହୁଅନ୍ତି, ଅର୍ଥାତ୍ ଗୋଟିକର ବୃଦ୍ଧି ବା ହ୍ରାସ ସହ ଅନ୍ୟଟିର ବୃଦ୍ଧି ହ୍ରାସ ସମକାଳୀନ ହୋଇଥାଏ, ତାହାକୁ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

୮। ଶୈଖକ ସହସମ୍ବନ୍ଧ କ’ଣ ?
Answer:
ଯେତେବେଳେ ରାଶିଦ୍ଵୟର ପରିବର୍ତ୍ତନ ଏକ ସ୍ଥିର ଅନୁପାତରେ ଘଟେ ତାହାକୁ ବୈଖକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

୯। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ କ’ଣ ?
Answer:
ଯାହା ମାଧ୍ୟମରେ ରାଶିଦ୍ଵୟରେ ରହିଥିବା ପାରସ୍ପରିକ ସଂପର୍କର ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣାତ୍ମକ ପରିପ୍ରକାଶ କରାଯାଏ,

୧୦ । ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯଦି କୌଣସି ରାଶିର ବୃଦ୍ଧି ବା ହ୍ରାସ ସହ ଅନ୍ୟ ରାଶିଟିର ବୃଦ୍ଧି ଓ ହ୍ରାସ ସ୍ଥିର ଅନୁପାତରେ ଘଟିଥାଏ, ତାହାକୁ ରାଶି ମଧ୍ୟରେ ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ ରହିଛି ବୋଲି କୁହାଯାଏ।

୧୧। ପୂର୍ଣ ସହସମ୍ବନ୍ଧ କେତେ ପ୍ରକାର ?
Answer:
ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ ଦୁଇ ପ୍ରକାର; ଯଥା – ଧନାତ୍ମକ ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ ଓ ଋଣାତ୍ମକ ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ ।

୧୨। ଧନାତ୍ମକ ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ କ’ଣ ?
Answer:
ଯେତେବେଳେ ଗୋଟିଏ ରାଶିର ବୃଦ୍ଧି ବା ହ୍ରାସ ସହ ଅନ୍ୟରାଶିର ଯଥାକ୍ରମେ ବୃଦ୍ଧି ବା ହ୍ରାସ ପରିଲକ୍ଷିତ ହୁଏ

୧୩। ଋଣାତ୍ମକ ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ କ’ଣ ?
Answer:
ଯେତେବେଳେ ରାଶି ଦ୍ବୟର ପରିବର୍ତ୍ତନ ବିପରୀତ ଦିଗରେ ସଂଗଠିତ ହୁଏ; ଯଥା – ଗୋଟିଏ ରାଶିର ବୃଦ୍ଧି ବା ହ୍ରାସ ସହ ଅନ୍ୟ ରାଶିର ଯଥାକ୍ରମେ ହ୍ରାସ ଓ ବୃଦ୍ଧି ଘଟେ ତାହାକୁ ଋଣାତ୍ମକ ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

୧୪। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ସର୍ବାଧ‌ିକ ମୂଲ୍ୟକେତେ ହୋଇପାରେ ?
Answer:
+୧

୧୫। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ ‘୦’ ହେଲେ କି ପ୍ରକାର ସିଦ୍ଧାନ୍ତ ନିଆଯାଇପାରେ ?
Answer:
ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ‘୦’ ହେଲେ, ଦୁଇଟି ରାଶି ମଧ୍ୟରେ ପାରସ୍ପରିକ ସଂପର୍କ ନଥବାର ସିଦ୍ଧାନ୍ତ ନିଆଯାଇପାରେ।

୧୬। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ ୯୮ ହେଲେ କି ପ୍ରକାର ସିଦ୍ଧାନ୍ତ ଗ୍ରହଣ କରାଯାଇପାରେ ?
Answer:
ରାଶିଦ୍ଵୟ ମଧ୍ଯରେ ଅଧିକ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ରହିଛି।

୧୭। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ –୧ ହେଲେ ରାଶିଦ୍ଵୟ ମଧ୍ଯରେ କି ପ୍ରକାର ସଂପର୍କ ରହିଛି ?
Answer:
ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ – ୧ ହେଲେ ରାଶିଦ୍ଵୟ ମଧ୍ୟରେ ପୂର୍ଣ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ ରହିଛି।

୧୮। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ ପାଇଁ ପ୍ରଣୟନ କରିଥିବା ସୂତ୍ରର ଏକ ମୁଖ୍ୟ ପ୍ରଣେତାଙ୍କ ନାମ କ’ଣ ?
Answer:
କାଇଁ ପିଅରସନ।

୧୯ । ସମାଶ୍ରୟଣ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ହାରାହାରୀ ସମ୍ପର୍କକୁ ସମାଶ୍ରୟଣ କୁହାଯାଏ ।

୨୦ । ସହସମ୍ପର୍କର ଗୁଣାଙ୍କ କିପରି ମିଳିଥାଏ ?
Answer:
ଦୁଇଟି ସମାଶ୍ରୟତା ଗୁଣାଙ୍କର ଗୁଣଫଳର ବର୍ଗମୂଳ ନେଇ ସହସମ୍ପର୍କ ଗୁଣାଙ୍କ ମିଳିଥାଏ ।

D. ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକ ଭୁଲ କି ଠିକ୍ ଲେଖ । ରେଖାଙ୍କିତ ଅଂଶର ପରିବର୍ତ୍ତନ ନ କରି ଆବଶ୍ୟକ ସ୍ଥଳେ ସଂଶୋଧନ କର ।

୧। ଚାହିଦା ଓ ଦର ମଧ୍ଯରେ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ଥାଏ।
Answer:
ଚାହିଦା ଓ ଦର ମଧ୍ଯରେ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ ଥାଏ।

୨। ଉଚ୍ଚ ସହ ସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ +୧ ସଂଖ୍ୟାର ନିକଟରେ ଥାଏ।
Answer:
ଉଚ୍ଚ ସହ ସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ + ୧ ସଂଖ୍ୟାର ନିକଟରେ ଥାଏ।

୩। ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ସହସମ୍ବନ୍ଧ ନ ଥିଲେ ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ ୧ ହୋଇଥାଏ।
Answer:
ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ସହସମ୍ବନ୍ଧ ନ ଥିଲେ ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ମୂଲ୍ୟ ୦ ହୋଇଥାଏ

୪। ଦର ଓ ଯୋଗାଣ ମଧ୍ଯରେ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ ପରିଲକ୍ଷିତ ହୋଇଥାଏ।
Answer:
ଦର ଓ ଯୋଗାଣ ମଧ୍ଯରେ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ପରିଲକ୍ଷିତ ହୋଇଥାଏ।

୫। ଦୁଇଟି ଚଳ ଥବା ବଣ୍ଟନକୁ ବିଚଳ ବଣ୍ଟନ କୁହାଯାଏ।
Answer:
ଦୁଇଟି ଚଳ ଥବା ବଣ୍ଟନକୁ ଦ୍ଵିବିଚଳ (bivariate distribution) ବଣ୍ଟନ କୁହାଯାଏ।

୬। ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ଥିବା ସମ୍ବନ୍ଧକୁ ଏକାଧିକାର ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।
Answer:
ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ଥିବା ସମ୍ବନ୍ଧକୁ ସରଳ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

୭। ବିପରୀତ ଦିଗରେ ପରିବର୍ତ୍ତିତ ହେଉଥୁବା ଚଳମାନଙ୍କର ସହସମ୍ବନ୍ଧକୁ ଧନାକତ୍ମ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।
Answer:
Answer:
ବିପରୀତ ଦିଗରେ ପରିବର୍ତ୍ତିତ ହେଉଥୁବା ଚଳମାନଙ୍କର ସହସମ୍ବନ୍ଧକୁ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

୮। ଯେଉଁ ଚିତ୍ରଲେଖ ସାହାଯ୍ୟରେ ସହସମ୍ବନ୍ଧର ଧାରଣା କରିହୁଏ ତାହାକୁ ବକ୍ରରେଖକ ଚିତ୍ର କହନ୍ତି ।
Answer:
ଯେଉଁ ଚିତ୍ରଲେଖ ସାହାଯ୍ୟରେ ସହସମ୍ବନ୍ଧର ଧାରଣା କରିହୁଏ ତାହାକୁ ବିକ୍ଷିପ୍ତ ରେଖାଚିତ୍ର କହନ୍ତି ।

୯ । ଅନେକ ଚଳମାନଙ୍କ ମଧ୍ୟରେ ଯେଉଁ ସହସମ୍ବନ୍ଧ ପରିଲକ୍ଷିତ ହୁଏ ତାହାକୁ ଆଂଶିକ ସହସମ୍ବନ୍ଧ କହନ୍ତି ।
Answer:
ଅନେକ ଚଳମାନଙ୍କ ମଧ୍ୟରେ ଯେଉଁ ସହସମ୍ବନ୍ଧ ପରିଲକ୍ଷିତ ହୁଏ, ତାହାକୁ ଏକାଧିକ ସହସମ୍ବନ୍ଧ କହନ୍ତି ।

୧୦। \(\frac{\Delta Y}{\Delta X}\) ଯଦି ଧବଙ୍କ ( ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଏକକ) ହୋଇଥାଏ ତା’ ହେଲେ X ଓ Y ମଧ୍ୟରେ ସରଳରେଖକ ସହସମ୍ବନ୍ଧ ଥାଏ।
Answer:
ଠିକ୍

୧୧। ସହସମ୍ବନ୍ଧ ମାଧ୍ୟମରେ ରାଶିଦ୍ଵୟ ମଧ୍ଯରେ ରହିଥିବା ଗୁଣାତ୍ମକ ସଂପର୍କ ନିର୍ଦ୍ଧାରଣ କରାଯାଇଥାଏ।
Answer:
ଯେତେବେଳେ ରାଶିଦ୍ଵୟର ପରିବର୍ତ୍ତନ ସ୍ଥିର ଅନୁପାତରେ ହୁଏ, ତାହାକୁ ବୈଖକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

୧୨। ଯେତେବେଳେ ରାଶିଦୁର ପରିବର୍ତ୍ତନ ସ୍ଥିର ଅନୁପାତରେ ହୁଏ, ତାହାକୁ ସରଳ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।
Answer:
ଯେତେବେଳେ ରାଶିଦ୍ବୟର ପରିବର୍ତ୍ତନ ସ୍ଥିର ଅନୁପାତରେ ହୁଏ, ତାହାକୁ ବୈଖ୍ୟକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

୧୩। ଅଣରେଖକ ସହସମ୍ବନ୍ଧ କ୍ଷେତ୍ରରେ ଦୁଇଟି ପରିବର୍ତ୍ତନ ହାର ଅସମାନୁପାତିକ।
Answer:
ଠିକ୍

୧୪। ସହସମ୍ବନ୍ଧର ଗୁଣାଙ୍କ ମୂଲ୍ୟର ସୀମା –୧ରୁ ୦ ମଧ୍ୟରେ ହୋଇଥାଏ।
Answer:
ସହସମ୍ବନ୍ଧର ଗୁଣାଙ୍କ ମୂଲ୍ୟର ସୀମା –୧ରୁ +୧ ମଧ୍ୟରେ ହୋଇଥାଏ।

୧୫। ଏକାଧ‌ିକ ସହସମ୍ବନ୍ଧରେ ଦୁଇଟି ରାଶିର ପରିବର୍ତ୍ତନ ଅନୁପାତ ସ୍ଥିର ରହେ।
Answer:
ସରଳ ରେଖକ ସମ୍ବନ୍ଧରେ ଦୁଇଟି ରାଶିର ପରିବର୍ତ୍ତନ ଅନୁପାତ ସ୍ଥିର ରହେ।

୧୬ । ସମାଶ୍ରୟଣଦ୍ୱାରା ଫଳନକୁ ବ୍ୟବହାର କରି ସ୍ୱତନ୍ତ୍ର ଚଳର ମୂଲ୍ୟର ଭବିଷ୍ୟ କଥନ କରିହୁଏ ।
Answer:
ସମାଶ୍ରୟଣଦ୍ୱାରା ଫଳନକୁ ବ୍ୟବହାର କରି ନିର୍ଭରଶୀଳ ଚଳର ମୂଲ୍ୟର ଭବିଷ୍ୟ କଥନ କରିହୁଏ ।

E. ପାଞ୍ଚଟି ବାକ୍ୟ ମଧ୍ଯରେ ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନମାନଙ୍କ ଉତ୍ତର ଦିଅ ।

୧। ସହସମ୍ବନ୍ଧ କ’ଣ ?
Answer:
ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ଥ‌ିବା ସମ୍ବନ୍ଧକୁ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ। ଯଦି ଗୋଟିଏ ଚଳରେ ପରିବର୍ତ୍ତନ ଯୋଗୁଁ ଅନ୍ୟ ଏକ ଚଳରେ ପରିବର୍ତ୍ତନ ହୁଏ, ସେହି ଚଳଦ୍ଵୟର ସମ୍ପର୍କକୁ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ। କ୍ରକ୍ୱଟନ୍ ଓ କଉଡେନ୍‌ଙ୍କ ଅନୁଯାୟୀ ଯେତେବେଳେ ସମ୍ବନ୍ଧ ପରିମାଣତ୍ମକ ହୋଇଥାଏ, ସମ୍ବନ୍ଧର ପରିମାପ ଓ ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀରେ ବ୍ୟକ୍ତ କରିବା ପାଇଁ ବ୍ୟବହୃତ ଉପଯୁକ୍ତ ପରିସଂଖ୍ୟାନ ସମ୍ବନ୍ଧୀୟ ଉପକରଣକୁ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ। ସୁତରାଂ ସହସମ୍ବନ୍ଧ ହେଉଛି ଏକ ବିଶ୍ଳେଷଣ ପଦ୍ଧତି ଯହିଁରେ ଦୁଇ ବା ତତୋଽଧୂକ ଚଳମାନଙ୍କ ମଧ୍ୟରେ ସହମାନ ପରିବର୍ତ୍ତନର ବିଶ୍ଳେଷଣ କରାଯାଇଥାଏ।

୨। ସହସମ୍ବନ୍ଧର ଉପଯୋଗିତା କ’ଣ ?
Answer:

• ସହସମ୍ବନ୍ଧର ପ୍ରକ୍ରିୟାରେ ରାଶିମାନଙ୍କ ମଧ୍ୟରେ ରହିଥିବା ପାରସ୍ପରିକ ସଂର୍ପକର ମାତ୍ରାକୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟାରେ ପରିପ୍ରକାଶ କରାଯାଇଥାଏ ।
• ସହସମ୍ବନ୍ଧ ପ୍ରକ୍ରିୟାରେ ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଥ‌ିବା ଗୋଟିଏ ରାଶିର ମୂଲ୍ୟ ଜଣାଥଲେ ଅନ୍ୟ ରାଶିର ମୂଲ୍ୟ ଆକଳନ କରାଯାଇଥାଏ ।
• ବ୍ୟବସାୟିକ ଉତ୍‌ଥାନ ପତନ, ଅର୍ଥନୈତିକ ପ୍ରକ୍ରିୟାରେ ଏହା ବିଶେଷ ଉପଯୋଗୀ।

୩। ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ କ’ଣ ?
Answer:
ଯଦି ଦୁଇଟି ଚଳ ସମଦିଗରେ ପରିବର୍ତ୍ତନ ହୁଏ, ତେବେ ଚଳଦ୍ଵୟ ମଧ୍ଯରେ ସମ୍ପର୍କକୁ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ। ଅର୍ଥାତ୍ ଯଦି ଗୋଟିଏ ଚଳରେ ବୃଦ୍ଧି ଘଟିବା ଯୋଗୁଁ ଅନ୍ୟ ଚଳଟିର ବୃଦ୍ଧି ଘଟେ କିମ୍ବା ଯଦି ଗୋଟିଏ ଚଳରେ ହ୍ରାସ ଯୋଗୁଁ ଅନ୍ୟ ଚଳରେ ମଧ୍ୟ ହ୍ରାସ ଘଟେ, ତେବେ ସେହି ଚଳଦ୍ଵୟ ମଧ୍ଯରେ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ରହେ। ଦ୍ରବ୍ୟର ଦର ଓ ଦ୍ରବ୍ୟର ଯୋଗାଣ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧର ଏକ ଉଦାହରଣ।

୪। ରେଖକ ସହସମ୍ବନ୍ଧ କ’ଣ ?
Answer:
ଗୋଟିଏ ଚଳର ଏକକ ପରିବର୍ତ୍ତନ ସହିତ ଅନ୍ୟ ଚଳରେ ସର୍ବଦା ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାତ୍ରାର ପରିବର୍ତ୍ତନ ଦେଖାଦେଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ସହସମ୍ବନ୍ଧକୁ ବୈଖ୍ୟକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ। ଉଦାହରଣ ସ୍ଵରୂପ ଯଦି କୌଣସି ସମୟରେ ଦାମ୍‌ର ଶତକଡ଼ା ୧୦ ବୃଦ୍ଧି ହୁଏ, ଏହାର ଯୋଗାଣର ୨୦% ବୃଦ୍ଧି ଘଟାଏ ଓ ଏହି ଅନୁପାତ ସ୍ଥିର ରହେ ତେବେ ଏହା ରିଖକ ସହସମ୍ବନ୍ଧର ଉଦାହରଣ ଦର୍ଶାଇଥାଏ। ଏହି ରାଶିଦ୍ଵୟର ମୂଲ୍ୟକୁ କ୍ରମାନ୍ଵୟରେ ଏକ ଗ୍ରାଫ୍ କାଗଜରେ ସ୍ଥାପିତ କଲେ ତାହା ମଧ୍ୟରେ ଏକ ସରଳ ରେଖାର ଚିତ୍ର ପ୍ରତିଫଳିତ ହୋଇଥାଏ।

୫। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ କ’ଣ ?
Answer:
କୌଣସି ଏକ ବିତରଣ ମାଳାର ଦତ୍ତ ଥବା ରାଶିଦ୍ଵୟ ମଧ୍ଯରେ ରହିଥ‌ିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧର ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣାତ୍ମକ ପରିପ୍ରକାଶ ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ ମାଧ୍ୟମରେ କରାଯାଇଥାଏ। ଏହା ସତ୍ୟ ଯେ ରାଶିଦ୍ଵୟ ମଧ୍ଯରେ ରହିଥିବା ସମ୍ବନ୍ଧ ସ୍ଥିର ନୁହେଁ। ଅଥବା ରାଶିଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ମୂଲ୍ୟ ଦତ୍ତ ଥିଲେ ଅନ୍ୟଟିର ମୂଲ୍ୟ ଗଣନା କରିବା ସର୍ବଦା ସମ୍ଭବପର ନୁହେଁ। ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ ‘r’ ଦ୍ଵାରା ଚିହ୍ନିତ ହୋଇଥଶଏ। ଏହାର ମୂଲ୍ୟ +୧ ରୁ –୧ ହୋଇଥାଏ। ଯେତେବେଳେ r = 0 ହୁଏ ସେ ସମୟରେ ରାଶିଦ୍ଵୟ ମଧ୍ୟରେ କୌଣସି ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ନ ଥାଏ।

୬। କାର୍ଲ ପିଅରସନଙ୍କ ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ କାହାକୁ କୁହାଯାଏ ?
Answer:
ସହସମ୍ବନ୍ଧର ମାତ୍ରା ପରିମାପ କରିବା ପାଇଁ ବ୍ରିଟିଶ୍ ପରିସଂଖ୍ୟାନବିତ୍ କାର୍ଲ ପିଅରସନ ଏକ ଗାଣିତିକ ସୂତ୍ରର ଅବତାରଣା କରିଥିଲେ । ତାଙ୍କରି ନାମାନୁସାରେ ଏହି ସୂତ୍ରକୁ କାର୍ଲ ପିଅସରନଙ୍କ ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ ବୋଲି କୁହାଯାଏ । X ଓ Y ଦୁଇଟି ଚଳର ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କର ସାଧାରଣତଃ rxy ବା କେବଳ ‘r’ ଅକ୍ଷର ଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଇଥାଏ।

ଏହା ଦୁଇଟି ଚଳରାଶିର ସରଳ ରୈଖ୍ୟକ ସହସମ୍ବନ୍ଧ ମାତ୍ରାକୁ ସୂଚିତ କରେ । ପିଅରସନଙ୍କ ଅନୁସାରେ ଏହି ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ ଚଳରାଶିଦ୍ଵୟର ସହପ୍ରସରଣ ଓ ସେମାନଙ୍କର ମାନକ ବିଚ୍ୟୁତି ଦ୍ଵୟର ଗୁଣଫଳର ଅନୁପାତକୁ ବୁଝାଇଥାଏ।

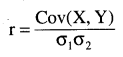
r = ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ Cov (X.Y) –X ଓ Y ର ସହପ୍ରସରଣ, 6₁ = X ର ମାନକ ବିଚ୍ୟୁତି, 6₂ = Y ର ମାନକ ବିଚ୍ୟୁତି ।

୭। ସମାଶ୍ରୟଣ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ଥ‌ିବା ହାରାହାରି ସମ୍ପର୍କକୁ ସମାଶ୍ରୟଣ କୁହାଯାଏ । ଏହା ଆକଳନ ଓ ଭବିଷ୍ୟତ କଥନରେ ବହୁଳ ଭାବରେ ବ୍ୟବହାର ହୋଇଥାଏ ।

E. ତିନୋଟି ବାକ୍ୟରେ ସୀମିତ ରଖ୍ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।

୧। ଧନାତ୍ମକ ଓ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ
Answer:
ଚଳଗୁଡ଼ିକର ପରିର୍ତ୍ତନର ଦିଗ ଭିତ୍ତିରେ ସହସମ୍ବନ୍ଧ ଧନାତ୍ମକ କିମ୍ବା ଋଣାତ୍ମକ ହୋଇଥାଏ। ଯଦି ଦୁଇଟି ଚଳ ସମଦିଗରେ ପରିବର୍ତ୍ତନ ହୁଏ, ତେବେ ଚଳଦ୍ଵୟ ମଧ୍ଯରେ ସମ୍ପର୍କକୁ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ। ଅର୍ଥାତ୍ ଯଦି ଗୋଟିଏ ଚଳରେ ହ୍ରାସ ବା ବୃଦ୍ଧି ଘଟିବା ଯୋଗୁଁ ଅନ୍ୟ ଚଳଟିର ହ୍ରାସ ବା ବୃଦ୍ଧି ଘଟେ; ତେବେ ସେହି ଚଳଦ୍ଵୟ ମଧ୍ଯରେ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ରହେ। ଦ୍ରବ୍ୟର ଦର ଓ ତେବେ ଚଳଦ୍ଵୟ ମଧ୍ୟରେ ସମ୍ପର୍କକୁ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

ଅର୍ଥାତ୍ ଯଦି ଗୋଟିଏ ଚଳରେ ବୃଦ୍ଧି ଘଟେ ଓ ଅନ୍ୟ ଚଳଟିର ହ୍ରାସ ଘଟେ କିମ୍ବା ଗୋଟିଏ ଚଳରେ ହ୍ରାସ ଘଟେ ଓ ଅନ୍ୟଚଳଟିର ବୃଦ୍ଧି ଘଟେ, ତେବେ ସେହି ଚଳଦ୍ଵୟ ମଧ୍ଯରେ ସମ୍ପର୍କକୁ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ । ଦ୍ରବ୍ୟର ଦର ଓ ଦ୍ରବ୍ୟର ଚାହିଦା ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧର ଏକ ଉଦାହରଣ।

୨। ସରଳରେଖକ ଓ ବକ୍ରରୈଖକ ସହସମ୍ବନ୍ଧ
Answer:
ଗୋଟିଏ ଚଳର ଏକକ ପରିବର୍ତ୍ତନ ସହିତ ଅନ୍ୟ ଚଳରେ ସର୍ବଦା ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାତ୍ରାର ପରିବର୍ତ୍ତନ ଦେଖାଦେଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସହସମ୍ବନ୍ଧକୁ ରେଖକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ। ସରଳରେଖକ ସହସମ୍ବନ୍ଧ ଥିବା ଦୁଇଟି ଚଳରାଶିର ମୂଲ୍ୟ ଗୁଡ଼ିକୁ ରେଖାଚିତ୍ରଦ୍ଵାରା ପ୍ରକାଶ କଲେ ତାହା ଏକ ସରଳରେଖା ହୋଇଥାଏ। ଅନ୍ୟ ପକ୍ଷରେ ଗୋଟିଏ ଚଳର ଏକକ ପରିବର୍ତ୍ତନ ଯୋଗୁଁ ଅନ୍ୟ ଚଳରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାତ୍ରାର ପରିବର୍ତ୍ତନ ଦେଖା ନ ଦେଇ ଭିନ୍ନ ଭିନ୍ନ ମାତ୍ରାର ପରିବର୍ତ୍ତନ ଦେଖାଦିଏ, ତେବେ ସେମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସହସମ୍ବନ୍ଧକୁ ବକ୍ରରେଖକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ।

ସେମାନଙ୍କର ମୂଲ୍ୟଗୁଡ଼ିକୁ ଚିତ୍ରରେଖା ଦ୍ଵାରା ପ୍ରକାଶ କଲେ ତାହା ଏକ ବକ୍ରରେଖାର ଆକୃତି ଧାରଣ କରିଥାଏ । X ଓ Y ଦୁଇଟି ଚଳରାଶି ହେଲେ ଏକଘାତୀ ସହସମ୍ବନ୍ଧ କ୍ଷେତ୍ରରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଏକକ ହୋଇଥାଏ । ସାଧାରଣତଃ ସେମାନଙ୍କ ସମ୍ପର୍କକୁ ଏକଘାତୀ ସମୀକରଣ Y = a + bx ଦ୍ଵାରା ପ୍ରକାଶିତ କରାଯାଇଥାଏ । X ଓ Y ଚଳଦ୍ଵୟ ମଧ୍ୟରେ ବକ୍ରରେଖକ ସହସମ୍ବନ୍ଧ ଥିଲେ \(\frac{\Delta Y}{\Delta X}\) ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଏକକ ନ ହୋଇ ଏକ ଚଳରାଶି ହୋଇଥାଏ ।

୩। ସମ୍ପୂର୍ଣ୍ଣ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ଓ ସମ୍ପୂର୍ଣ୍ଣ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ
Answer:
ଚଳ ଦୁଇଟିର ମୂଲ୍ୟ ଦର୍ଶାଉଥବା ଲେଖବିନ୍ଦୁ ସବୁ ଗୋଟିଏ ସରଳରେଖାରେ ବିଦ୍ୟମାନ ହେଲେ ଚଳ ଦୁଇଟି ମଧ୍ୟରେ ସମ୍ପୂର୍ଣ୍ଣ ସହସମ୍ବନ୍ଧ ରହିଛି ବୋଲି କୁହାଯାଏ। ଏହା ଧିନାତ୍ମକ ଅଥବା ଋଣାତ୍ମକ ହୋଇପାରେ। ସେହି ସରଳରେଖା ବାମରୁ ଡାହାଣକୁ ଉର୍ଦ୍ଧ୍ୱଗାମୀ ହେଲେ ଚଳ ଦୁଇଟି ମଧ୍ୟରେ ସମ୍ପୂର୍ଣ୍ଣ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ରହିଥାଏ। ମାତ୍ର ଲେଖବିନ୍ଦୁ ସବୁକୁ ଧାରଣ ଡାହାଣକୁ ଉର୍ଦ୍ଧ୍ୱଗାମୀ ହେଲେ ଚଳ ଦୁଇଟି ମଧ୍ୟରେ ସମ୍ପୂର୍ଣ୍ଣ ଧନାତ୍ମକ ସହସମ୍ବନ୍ଧ ରହିଥାଏ।

ମାତ୍ର ଲେଖବିନ୍ଦୁ ସବୁକୁ ଧାରଣ ରେଖାଚିତ୍ର ପଦ୍ଧତିରେ ଚଳ ଦୁଇଟିର କ୍ରମିକ ମୂଲ୍ୟସବୁକୁ ଲେଖବିନ୍ଦୁ ଆକାରରେ ଉପସ୍ଥାପନ କରିବାକୁ ପଡ଼େ । ଏପରିଭାବେ ଅଙ୍କିତ ବନ୍ଧୁଗୁଡ଼ିକ ପରସ୍ପରର ଅଡ଼ି ନିକଟତର ହେଲେ ଚଳ ଦୁଇଟି ମଧ୍ୟରେ ସହସମ୍ବନ୍ଧର ମାତ୍ରା ଅଧିକ ହୋଇଥାଏ । ଅନ୍ୟପକ୍ଷରେ ବିନ୍ଦୁଗୁଡ଼ିକ ପରସ୍ପରଠାରୁ ବିକ୍ଷିପ୍ତ ହୋଇ ରହିଲେ ଚଳ ଦୁଇଟି ମଧ୍ୟରେ ସହସମ୍ବନ୍ଧର ମାତ୍ରା କମ୍ ହୋଇଥାଏ ।

୪। ଉଚ୍ଚ ସହସମ୍ବନ୍ଧ ଓ ନିମ୍ନ ସହସମ୍ବନ୍ଧ
Answer:
ଦୁଇ ବା ତତୋଧ୍ଵକ ଚଳରାଶିମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ଓ ତାହାର ମାତ୍ରାକୁ ମାପ କରିବାପାଇଁ ଯେଉଁ ସାଂଖ୍ୟକ ପଦ୍ଧତିର ସାହାଯ୍ୟ ନିଆଯାଏ, ତାହାକୁ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ । ଯଦି ଗୋଟିଏ ଚଳରାଶିର ପରିବର୍ତ୍ତନ ଫଳରେ ଅନ୍ୟ ଗୋଟିଏ ଚଳରାଶିର ବହୁ ପରିମାଣରେ ପରିବର୍ତ୍ତନ ଘଟେ ତାହାହେଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ ଉଚ୍ଚ ସହସମ୍ବନ୍ଧ ରହିଥାଏ। ଏହା ଧନାତ୍ମକ ଯୋଗୁଁ ଅନ୍ୟ ଚଳରାଶିର ସ୍ଵଳ୍ପ ପରିବର୍ତ୍ତନ ଘଟିଲେ ସେମାନଙ୍କର ସହସମ୍ବନ୍ଧ ମାତ୍ରା ନିମ୍ନ ହୋଇଥାଏ। ଏହା ମଧ୍ୟ ଧନାତ୍ମକ ଅଥବା ଋଣାତ୍ମକ ହୋଇପାରେ।

୫। ସହସମ୍ବନ୍ଧର ମାତ୍ରା ଓ ସହସମ୍ବନ୍ଧର ଅଭାବ
Answer:
ଏଠାରେ କେବଳ ଚଳମାନଙ୍କର ସରଳରେଖକ ସହସମ୍ବନ୍ଧ ସହ ସଂଶ୍ଳିଷ୍ଟ । ସୁତରାଂ ଚଳମାନଙ୍କର ଏକ ବିକୀର୍ଣନ ଆରେଖ ଅଙ୍କନ କଲେ ଯଦି ବିନ୍ଦୁ ଗୁଡ଼ିକ ଏକ ସରଳରେଖାର ଖୁବ୍ ନିକଟରେ ଅବସ୍ଥାପିତ ହୁଅନ୍ତି ତାହାହେଲେ ସେମାନଙ୍କର ସହସମ୍ବନ୍ଧ ମାତ୍ରା ସେତେ ଅଧ୍ଵକ ହୋଇଥାଏ। ଅନ୍ୟ ପକ୍ଷରେ ଯଦି ବିନ୍ଦୁଗୁଡ଼ିକ ସରଳରେଖାର ଦୂରରେ ବିକ୍ଷିପ୍ତ ହୋଇଥାନ୍ତି ତେବେ ଚଳମାନଙ୍କର ସହସମ୍ବନ୍ଧ ମାତ୍ରା କମ୍ ହୋଇଥାଏ। ସୁତରାଂ ସହସମ୍ବନ୍ଧର ବିଭିନ୍ନ ଦିଗ ଓ ମାତ୍ରା ସମ୍ପର୍କରେ ଜାଣିବା ଏକାନ୍ତ ଆବଶ୍ୟକ ।

ଯଦି ଗୋଟିଏ ଚଳରାଶିର ପରିବର୍ତ୍ତନ ଅନ୍ୟ ଚଳରାଶିର ପରିବର୍ତ୍ତନରେ ଉଦାସୀନ ଥିଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ ସହସମ୍ବନ୍ଧର ଅଭାବ ଥାଏ ବୋଲି କୁହାଯାଏ।

୬। ସହସମ୍ବନ୍ଧ ଓ ସହକାରଣ
Answer:
ସହସମ୍ବନ୍ଧ ଓ ସହକାରଣ ଶବ୍ଦ ଦୁଇଟି ପରିସଂଖ୍ୟାନରେ ସାଧାରଣଭାବେ ବ୍ୟବହାର ହେଲେ ମଧ୍ୟ ଉଭୟଙ୍କ ମଧ୍ୟରେ ବ୍ୟବହାରିକ ପାର୍ଥକ୍ୟ ରହିଛି । ସହସମ୍ବନ୍ଧ କ୍ଷେତ୍ରରେ ଦୁଇଟି ଚଳ ପରସ୍ପର ମଧ୍ୟରେ ସମ୍ପର୍କିତ କିନ୍ତୁ କାରଣ ଓ ଫଳାଫଳ ଭିଭିକ ସମ୍ପର୍କ ନ ଥାଏ । ଅନ୍ୟପକ୍ଷରେ ସହକାରଣରେ ଗୋଟିଏ ଚଳ ଅନ୍ୟ ଚଳ ଉପରେ ପ୍ରଭାବ ପକାଇଥାଏ । ଉଦାହରଣ ସ୍ୱରୂପ, ବ୍ୟକ୍ତିର ଖାଦ୍ୟ ଓ ସ୍ୱାସ୍ଥ୍ୟ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କକୁ ସହସମ୍ପର୍କ କୁହାଯାଏ । କିନ୍ତୁ ସ୍ୱାସ୍ଥ୍ୟ ଓ ଖାଦ୍ୟ ମଧ୍ୟରେ ସହକାରଣ ନଥାଇପାରେ ।

ସହକାରଣ କ୍ଷେତ୍ରରେ ଗୋଟିଏ ଚଳକୁ ସ୍ଵତନ୍ତ୍ର ଚଳ ଓ ଅନ୍ୟ ଚଳକୁ ନିର୍ଭରଶୀଳ ଚଳ କୁହାଯାଏ । ତେଣୁ ସହକାରଣ ଥିଲେ ସହସମ୍ବନ୍ଧର ନିଶ୍ଚୟ ରହିବ ଯଦି ସହସମ୍ପଦ ଓ ସହକାରଣ ଏକା ସମୟରେ ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ଥାଏ, ଅନ୍ୟ ଏକ ବିଶେଷ କଥା ହେଲା – ସହକାରଣ ଥିଲେ ଭବିଷ୍ୟ ଗଣନା କରିବା ସମ୍ଭବ କିନ୍ତୁ ସହସମ୍ବନ୍ଧରେ ସେ ଭବିଷ୍ୟ କଳନା କରିହୁଏ ନାହିଁ ।

୭। ସହସମ୍ପର୍କ ଓ ସମାଶ୍ରୟଣ
Answer:
ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ଥ‌ିବା ସମ୍ପର୍କ ଜାଣିବା ପାଇଁ ଉଭୟ ସହସମ୍ବନ୍ଧ ଓ ସମାଶ୍ରୟଣ ପରିସଂଖ୍ୟାନରେ ଅତ୍ୟନ୍ତ ଉପଯୋଗୀ ପଦ୍ଧତି । କିନ୍ତୁ ଭିନ୍ନ ଭିନ୍ନ ସର୍ଭ ସମୂହରେ ଉଭୟ ପଦ୍ଧତି ପର୍ଯ୍ୟବସିତ । ସହସମ୍ପର୍କ ମାଧ୍ୟମରେ ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ସମ୍ପର୍କର ମାତ୍ରା ମାପିହୁଏ । କିନ୍ତୁ ସମାଶ୍ରୟଣରେ ଏହା ସମ୍ଭବ ନୁହେଁ । ଏହା କେବଳ ଉଭୟ ଚଳ ମଧ୍ୟରେ ଥ‌ିବା ପ୍ରଭାବ ବିଷୟ ଜଣାଯାଏ । ଗୋଟିଏ ଚଳର ମୂଲ୍ୟକୁ ନେଇ ସହସମ୍ପର୍କ ପଦ୍ଧତିଦ୍ୱାରା ଭବିଷ୍ୟତ କଳନା କରିହୁଏ ନାହିଁ । ପରନ୍ତୁ ସମାଶ୍ରୟଣ ଦ୍ବାରା ଫଳନ ବ୍ୟବହାର କରି ନିର୍ଭରଶୀଳ ଚଳର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କରିହୁଏ ।

ସହସମ୍ପର୍କର ଗୁଣାଙ୍କ (x, ଏବଂ 1 ) ପ୍ରତିସାମ୍ୟ ଅଟେ । କିନ୍ତୁ ସମାଶ୍ରୟଣ ଗୁଣାଙ୍କ (b ଏବଂ b) ପ୍ରତିସାମ୍ୟ ନୁହେଁ । ଦୁଇଟି ଚଳ ମଧ୍ୟରେ ଅପ୍ରସିଦ୍ଧଙ୍କ ସମସମ୍ପର୍କ ଥାଇପାରେ କିନ୍ତୁ ସମାଶ୍ରୟଣ କ୍ଷେତ୍ରରେ ନୁହେଁ । ମୁଖ୍ୟ କଥା ଗୋଟିଏ ଶ୍ରେଣୀର ମୂଳବିନ୍ଦୁ ଓ ମାପକ୍ରମ ପରିବର୍ତ୍ତନ ହେଲେ ସହସମ୍ପର୍କର ଗୁଣାଙ୍କ ପରିବର୍ତ୍ତନ ହୁଏନାହିଁ, କିନ୍ତୁ ସମାଶ୍ରୟଣରେ ଗୁଣାଙ୍କ ପରିବର୍ତ୍ତନ ହୁଏ ।

ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

୧। ସହସମ୍ବନ୍ଧ (Correlation) କାହାକୁ କୁହାଯାଏ । ଏହାର ଉପଯୋଗିତା ବର୍ଣ୍ଣନା କର ।
Answer:
ଦୁଇ ବା ତତୋଧକ ପରିବର୍ତ୍ତନୀୟ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ସହ ସଂପର୍କର ମାତ୍ରା ସହସମ୍ବନ୍ଧ ବିଶ୍ଳେଷଣ ମାଧ୍ୟମରେ ଅଧ୍ୟୟନ କରାଯାଇଥାଏ । ସହସମ୍ବନ୍ଧ ଦୁଇ ବା ତତୋଽକ ଉପାଦାନ ମଧ୍ୟରେ ରହିଥ‌ିବା ସହସଂପର୍କ ବା ସହ ସଂଯୋଗର ଏକ ପରିମାଣାତ୍ମକ ପରିପ୍ରକାଶ କରିଥାଏ । ଯଦି ଦୁଇଟି ଉପାଦାନର ପରିମାଣାତ୍ମକ ପରିବର୍ତ୍ତନ ଏପରି ଘଟେ ଯେ ଯଦ୍ୱାରା ଏହି ଉପାଦାନ ଦ୍ବୟର ସମକାଳୀନ ପରିବର୍ତ୍ତନ ଘଟିଥାଏ ।

ଏହି ପରିବର୍ତ୍ତନ ମାତ୍ରାର ସଂଖ୍ୟକ ଅବତରଣ ସହସମ୍ବନ୍ଧ ବିଶ୍ଳେଷଣ ମାଧ୍ୟମରେ କରାଯାଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ କୌଣସି ଦ୍ରବ୍ୟର ଦାମ୍‌ର ପରିବର୍ତ୍ତନ ହେଲେ ଏହାର ଯୋଗାଣ ପରିମାଣରେ ସମକାଳୀନ ପରିବର୍ତ୍ତନ ଘଟିଥାଏ । ଏହି ପରିବର୍ତ୍ତନ ଏକ ଦିଗମୁଖ୍ୟ ହୋଇଥାନ୍ତି । ଏହି ପରିବର୍ତ୍ତନର ମାତ୍ରାକୁ ସହସମ୍ବନ୍ଧ ବିଶ୍ଳେଷଣ ଦ୍ଵାରା ପରିମାପ କରାଯାଇଥାଏ । ତେଣୁ ସହସମ୍ବନ୍ଧ ଅଧ୍ୟୟନରେ ଦୁଇ ବା ତତୋଧ୍ୱ ଉପାଦାନ ମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସଂପର୍କର ମାତ୍ରାର ସାଂଖ୍ୟକ ଉପସ୍ଥାପନ କରାଯାଇଥାଏ ।

ଏହି ପରିମାପକ ଉପାଦାନ ମାନଙ୍କର ପରିବର୍ତ୍ତନର ଦିଗ ଉପସ୍ଥାପନ କରିବା ସଂଗେ ସଂଗେ ସେମାନଙ୍କର ପରିବର୍ତ୍ତନ ମାତ୍ରା ମଧ୍ୟ ପରିପ୍ରକାଶ କରିଥାଏ । ସହସମ୍ବନ୍ଧର ଗାଣିତିକ ପଦ୍ଧତି ଅବଲମ୍ବନରେ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ରହିଥ‌ିବା ନିବିଡ଼ତାର ଏକ ସାଂଖ୍ୟକ ପ୍ରଦର୍ଶନ ହୋଇଥାଏ ।

• ସହସମ୍ବନ୍ଧ ଦୁଇ ବା ତତୋଧ‌ିକ ଉପାଦାନ ମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ସଂଯୋଗ ବା ସମନ୍ବୟ ବା ସହ ସଂପର୍କର ମାତ୍ରାକୁ ଅଧ୍ୟୟନ କରିଥାଏ ।
• ସହସମ୍ବନ୍ଧ (ସହସଂପର୍କ) ପରିବର୍ତ୍ତନୀୟ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ସହ ସଂଯୋଗ ବା ସହ ସଂପର୍କର ଏକ ସାଂଖ୍ୟକ ପରିପ୍ରକାଶ ।
• ଉପରୋକ୍ତ ପର୍ଯ୍ୟାଲୋଚନାରୁ ପ୍ରତୀୟମାନ ହୁଏ ଯେ କୋରିଲେସନ ଦୁଇ ବା ତତୋଧ୍ୱକ ପରିବର୍ତ୍ତନଶୀଳ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ଆନ୍ତଃସଂପର୍କକୁ ଅଧ୍ୟୟନ କରିଥାଏ ।

ଉପଯୋଗିତା :
ସମାଜ ବିଜ୍ଞାନ କ୍ଷେତ୍ରରେ କୋରିଲେସନ ଅଧ୍ୟୟନର ପ୍ରମୁଖ ଭୂମିକା ରହିଛି । ବାସ୍ତବ କ୍ଷେତ୍ରରେ ମଧ୍ୟ ସହସମ୍ବନ୍ଧ କେତେକ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଭୂମିକା ନିର୍ବାହ କରିଥାଏ । ଏହାର ବିଶେଷ ଉପଯୋଗିତା ନିମ୍ନରେ ବର୍ଣ୍ଣନା କରାଗଲା ।
(i) ସଂପର୍କର ସାଂଖ୍ୟକ ପରିପ୍ରକାଶ କରିଥାଏ – ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ସହ ସଂପର୍କର ମାତ୍ରାର ପରିମାଣାତ୍ମକ ପରିପ୍ରକାଶ ସହସମ୍ବନ୍ଧ ପଦ୍ଧତି ଅବଲମ୍ବନ ଦ୍ବାରା ସମ୍ଭବ ହୋଇଥାଏ । ଏହି ସହ ସଂପର୍କର ପରିପ୍ରକାଶ ପାଇଁ ଏକ ଗାଣିତିକ ପଦ୍ଧତି ଅବଲମ୍ବନ କରାଯାଇଥାଏ । ଏହି ଗାଣିତିକ ପଦ୍ଧତି ଦ୍ୱାରା ନିର୍ଦ୍ଧାରଣ ସହସମ୍ବନ୍ଧ ଗୁଣାଙ୍କ (r) ର ନିରୂପିତ ମୂଲ୍ୟ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ସଂପର୍କର ଦିଗ ଓ ମାତ୍ରା ଉପସ୍ଥାପନ କରିଥାଏ ।

ଯଦି r ର ମୂଲ୍ୟ + l ହୁଏ ତେବେ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ଏକ ପୂର୍ଣ୍ଣ ସହସଂପର୍କ ରହିଥାଏ ଏବଂ ଉପାଦାନମାନଙ୍କର ପରିବର୍ତ୍ତନ ଏକ ଦିଗରେ ହୋଇଥାଏ । ସେହିପରି r = 1 ହେଲେ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ଋଣାତ୍ମକ ସହ ସଂପର୍କ ରହିଥାଏ ଏବଂ ଉପାଦାନମାନଙ୍କର ପରିବର୍ତ୍ତନ ବିପରୀତ ଦିଗ ମୁଖୀ ହୋଇଥାଏ । r = 0 ହେଲେ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ କୌଣସି ପାରସ୍ପରିକ ସଂପର୍କ ନ ଥାଏ ।

(ii) ନିଷ୍ପତ୍ତି ଗ୍ରହଣରେ ସାହାଯ୍ୟ କରେ – କୌଣସି ଅର୍ଥନୈତିକ ପ୍ରକ୍ରିୟାରେ ନିଷ୍ପତ୍ତି ଗ୍ରହଣରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ଅନିଶ୍ଚିତତା ସହସମ୍ବନ୍ଧ ବିଶ୍ଳେଷଣ ଦ୍ଵାରା ଦୂରୀଭୂତ ହୋଇଥାଏ । ବ୍ୟବସାୟିକ କ୍ଷେତ୍ରରେ ଏହାର ଉପଯୋଗିତା ବିଶେଷ ଭାବେ ଉପଲବ୍‌ ହୋଇଥାଏ । ବିଶେଷକରି ବ୍ୟବସାୟିକ ପ୍ରାକ୍‌ସୂଚନା କୋରିଲେସନ ପଦ୍ଧତି ମାଧ୍ୟମରେ ମିଳିପାରିଥାଏ । ଏହି ପ୍ରାକ୍ ଆକଳନ ନିର୍ଭରଯୋଗ୍ୟ ହୋଇଥାଏ ।

(iii) ଅର୍ଥନୈତିକ ଆଚରଣ କ୍ଷେତ୍ରରେ ବିଶେଷ ଉପଯୋଗୀ – ସହସମ୍ବନ୍ଧ ଅଧ୍ୟୟନ ଅର୍ଥନୈତିକ ଆଚରଣ କ୍ଷେତ୍ରରେ ବିଶେଷ ସହାୟକ ହୋଇଥାଏ । ପାରସ୍ପରିକ ସଂପର୍କ ଥ‌ିବା ଉପାଦାନ ମାନଙ୍କର ଅର୍ଥନୈତିକ ପ୍ରକ୍ରିୟାରେ ସେମାନଙ୍କର ସ୍ଥିତି ଆକଳନ ସହସମ୍ବନ୍ଧ ବିଶ୍ଳେଷଣ ମାଧ୍ୟମରେ ହୋଇଥାଏ । ଅର୍ଥନୈତିକ ପ୍ରକ୍ରିୟାକୁ ପ୍ରଭାବିତ କରୁଥିବା ଉପାଦାନମାନଙ୍କ ସଂପର୍କରେ ସୂଚନା ଏହି ବିଶ୍ଳେଷଣରୁ ମିଳିଥାଏ ।

ଅର୍ଥନୈତିକ ସ୍ଥିରତାପାଇଁ ଆବଶ୍ୟକୀୟ ଉପାଦାନମାନଙ୍କୁ ଚିହ୍ନଟ କରିବାରେ ଏହି ପଦ୍ଧତିର ପ୍ରୟୋଗ କରାଯାଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ ମୁଦ୍ରାସ୍ପିତି ଘଟାଉଥିବା କିମ୍ବା ସ୍ବଳ୍ପ ଉତ୍ପାଦନର କାରଣ ସାଜିଥ‌ିବା ଉପାଦାନମାନଙ୍କ ସଂପର୍କରେ ଏହା ସମ୍ୟକ୍ ସୂଚନା ପ୍ରଦାନ କରିଥାଏ । ତେଣୁ ଅର୍ଥନୈତିକ ପ୍ରକ୍ରିୟାରେ ସ୍ଥିରତା ଆଣିବା କ୍ଷେତ୍ରରେ ଏହି ଗାଣିତିକ ପଦ୍ଧତିର ପ୍ରୟୋଗାତ୍ମକ ଭୂମିକା ରହିଛି ।

ପରିବର୍ଭନୀୟ ଉପାଦାନମାନଙ୍କର ପରିବର୍ତ୍ତନର ପରିମାପ – କୌଣସି ପ୍ରକ୍ରିୟାରେ ବିଶେଷ ଭୂମିକା ନିର୍ବାହ କରୁଥି ଉପାଦାନମାନଙ୍କର ନିବିଡ଼ତା ସଂପର୍କରେ ଏକ ପରିମାଣାତ୍ମକ ପରିପ୍ରକାଶ କରିଥାଏ । ଏତଦ୍‌ବ୍ୟତୀତ ଏହା ଉପାଦାନମାନଙ୍କର ପରିବର୍ତ୍ତନର ଦିଗ ସଂପର୍କରେ ମଧ୍ୟ ସୂଚନା ପ୍ରଦାନ କରିଥାଏ । ଉଦାହରଣସ୍ୱରୂପ, ଦାମ୍‌ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିବର୍ତ୍ତନ ଯୋଗୁ ଚାହିଦାର ପରିବର୍ତ୍ତନ ନିର୍ଦ୍ଧାରଣ କ୍ଷେତ୍ରରେ ସହସମ୍ବନ୍ଧର ଭୂମିକା ରହିଛି । ଉପରୋକ୍ତ ଆଲୋଚନାରୁ ସହସମ୍ବନ୍ଧର ବିଶେଷ ଭୂମିକା ସହଜରେ ଅନୁମେୟ ।

୨। ସହସମ୍ବନ୍ଧର ପ୍ରକାର ଭେଦ ବର୍ଣନା କର ।
Answer:
ସହସମ୍ବନ୍ଧ ବିଶ୍ଳେଷଣ ଦୁଇ ବା ତତୋଧ‌ିକ ଉପାଦାନ ମଧ୍ୟରେ ଥ‌ିବା ସଂପର୍କର ପରିମାଣାତ୍ମକ ପରିବର୍ତ୍ତନର ମାତ୍ରାର ପରିପ୍ରକାଶ କରିଥାଏ । ଏହି ସଂପର୍କର ସାଂଖ୍ୟକ ପରିପ୍ରକାଶ ବିଭିନ୍ନ ଭାବରେ ପ୍ରଦର୍ଶିତ ହୋଇଥାଏ । ନିମ୍ନରେ ପ୍ରଦତ୍ତ ସହସମ୍ବନ୍ଧର ପ୍ରକାର ଭେଦ ଏ ସଂପର୍କରେ ବିଷଦ ତଥ୍ୟ ପ୍ରଦାନ କରିଥାଏ ।

• ଯୋଗାତ୍ମକ ବା ଋଣାତ୍ମକ
• ସରଳ, ବହୁସ୍ତରୀୟ ଓ ଆଂଶିକ
• ରୈଖିକ ଓ ଅଣରୈଖିକ ।

(i) ଯୋଗାତ୍ମକ କିମ୍ବା ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ (Positive or Negative Correlation) –
ସହସମ୍ବନ୍ଧ ଯୋଗାତ୍ମକ କିମ୍ବା ଋଣାତ୍ମକ ହୋଇପାରେ, ଯେତେବେଳେ ଦୁଇଟି ଉପାଦାନର ପରିବର୍ତ୍ତନ ଏକ ଦିଗରେ । ହୁଏ ତାହାକୁ ଯୋଗାତ୍ମକ କୋରିଲେସନ କୁହାଯାଏ । ଏ କ୍ଷେତ୍ରରେ ଗୋଟିଏ ଉପାଦାନର ବୃଦ୍ଧି କିମ୍ବା ହ୍ରାସ ସହ ଅନ୍ୟଟିର ମଧ୍ୟ ଯଥାକ୍ରମେ ବୃଦ୍ଧି ବା ହ୍ରାସ ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ, ଦ୍ରବ୍ୟର ଦାମ୍ ଓ ଏହାର ଯୋଗାଣ ମଧ୍ଯରେ ଯୋଗାତ୍ମକ ସହସମ୍ବନ୍ଧ ଅନୁଭୂତ ହୋଇଥାଏ । ଉଭୟଙ୍କର ପରିବର୍ତ୍ତନ ସମଦିଗରେ ଘଟିଥାଏ ।

ଅନ୍ୟପକ୍ଷରେ ଯେତେବେଳେ ଦୁଇଟି ଉପାଦାନର ପରିବର୍ତ୍ତନର ଦିଗ ବିପରୀତମୁଖୀ ହୋଇଥାଏ ତାହାକୁ ଋଣାତ୍ମକ ସହସମ୍ବନ୍ଧ କୁହାଯାଏ । ଏ କ୍ଷେତ୍ରରେ ଗୋଟିଏ ଉପାଦାନର ପରିମାଣାତ୍ମକ ବୃଦ୍ଧି ସହ ଅନ୍ୟଟିରେ ପରିମାଣାତ୍ମକ ହ୍ରାସ ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ ଦ୍ରବ୍ୟର ଦାମ୍‌ରେ ହ୍ରାସ ଘଟିଲେ ଏହାର ଚାହିଦାର ପରିମାଣରେ ବୃଦ୍ଧି ଘଟିଥାଏ । ଏହା ଋଣାତ୍ମକ କୋରିଲେସନ ଦର୍ଶାଇଥାଏ ।

(ii) ସରଳ, ବହୁସ୍ତରୀୟ ଓ ଆଂଶିକ କୋରିଲେସନ – ଯେଉଁ କୋରିଲେସନ ପଦ୍ଧତିରେ ଦୁଇଟି ଉପାଦାନ ରହିଥାଏ, ତାହାକୁ ସରଳ କୋରିଲେସନ କୁହାଯାଏ । ଏହି ପଦ୍ଧତିରେ ଦୁଇଟି ଉପାଦାନ ମଧ୍ୟରେ ଥ‌ିବା ସହସଂପର୍କ ଦର୍ଶାଯାଇଥାଏ ।

ମାତ୍ର ଯେଉଁ କୋରିଲେସନ ବିଶ୍ଳେଷଣରେ ଦୁଇରୁ ଅଧୂକ ଉପାଦାନମାନଙ୍କରେ ଥ‌ିବା ସହ ସଂପର୍କର ଅଧ୍ୟୟନ କରାଯାଇଥାଏ ତାହାକୁ ବହୁସ୍ତରୀୟ (ବହୁମୁଖୀ) କୋରିଲେସନ କୁହାଯାଏ । ଉଦାହରଣସ୍ୱରୂପ ଉତ୍ପାଦନକୁ ପ୍ରଭାବିତ କରୁଥିବା ଅନେକ ଉପାଦାନମାନଙ୍କ ମଧ୍ୟରେ ସହ ସଂପର୍କ ରହିଥାଏ । ଏହା ବହୁସ୍ତରୀୟ (ବହୁମୁଖୀ) କୋରିଲେସନର ଉଦାହରଣ ।

ଆଂଶିକ କୋରିଲେସନ କ୍ଷେତ୍ରରେ ଦୁଇରୁ ଅଧିକ ଉପାଦାନ ରହିଥାଏ ମାତ୍ର ବିଶ୍ଳେଷଣ ପ୍ରକ୍ରିୟାରେ ଏହି ଉପାଦାନ ମାନଙ୍କ ମଧ୍ୟରୁ ଦୁଇଟି ଉପାଦାନ ମଧ୍ୟରେ ଥ‌ିବା ସଂପର୍କର ଅଧ୍ୟୟନ କରାଯାଇଥାଏ ଓ ଅନ୍ୟାନ୍ୟ ଉପାଦାନଗୁଡ଼ିକ ଅପରିବର୍ତ୍ତନୀୟ ବା ସ୍ଥିର ଉପାଦାନ ଭାବେ ଧରି ନିଆଯାଇଥାଏ ।

(iii) ରୈଖିକ ଏବଂ ଅଣରୈଖିକ କୋରିଲେସନ – ଯଦି ଦୁଇଟି ପରିବର୍ତ୍ତନୀୟ ଉପାଦାନ ଅପରିବର୍ତ୍ତନୀୟ ବା ସ୍ଥିର ଅନୁପାତରେ ଘଟିଥାଏ, ତାହାକୁ ଶୈଖିକ କୋରିଲେସନ କୁହାଯାଏ । ଏହି ପରିବର୍ତ୍ତନର ବିଭିନ୍ନ ମାତ୍ରାକୁ ରେଖାଚିତ୍ର ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଗଲେ ରେଖାଚିତ୍ରଟି ଏକ ସରଳରେଖା ହୋଇଥାଏ । ଯଦି ଦୁଇଟି ପରିବର୍ତ୍ତନୀୟ ଉପାଦାନରେ ପରିବର୍ତ୍ତନର ଅନୁପାତ ପରିବର୍ତ୍ତନଶୀଳ ହୁଏ, ତାହାକୁ ଅଣରୈଖିକ ସହସମ୍ପର୍କ କୁହାଯାଏ । ଉପରୋକ୍ତ ରୈଖିକ ସହସମ୍ପର୍କଟି କ୍ବଚିତ୍ ଦେଖାଯାଏ ।

୩। ସହସଂପର୍କ ଗୁଣାଙ୍କ କ’ଣ ? କାର୍ଲ ପିଅରସନ୍‌ଙ୍କ ଦ୍ବାରା ପ୍ରଣୀତ ସହସଂପର୍କ ଗୁଣାଙ୍କ ସଂପର୍କରେ ଆଲୋଚନା କର।
Answer:
ଦୁଇଟି ପରିବର୍ତ୍ତନୀୟ ଉପାଦାନ ମଧ୍ୟରେ ରହିଥ‌ିବା ସହସଂପର୍କର ମାତ୍ରା (Degree of correlation) କୁ ସହସଂପର୍କର ଗୁଣାଙ୍କ (correlation co-efficient) ମାଧ୍ୟମରେ ପରିପ୍ରକାଶ କରାଯାଇଥାଏ । ଦୁଇଟି ପରିବର୍ତ୍ତନୀୟ ରାଶି ମଧ୍ୟରେ ରହିଥ‌ିବା ସହସଂପର୍କ ସେମାନଙ୍କ ମଧ୍ୟରେ ରହିଥ‌ିବା ସଂପର୍କକୁ ଫଳନଯୁକ୍ତ (functional) ବା ସ୍ଥିର ବୋଲି ନିଶ୍ଚିତ ଭାବରେ ସୂଚାଇ ନଥାଏ । ଯଦି କୌଣସି ଗୋଟିଏ ରାଶିର ମୂଲ୍ୟ ଜଣାଥାଏ, ତେବେ ଅନ୍ୟ ରାଶିଟିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ ସର୍ବଦା ସମ୍ଭବ ହୋଇନଥାଏ । ଏହା କେବଳ ଦୁଇଟି ରାଶି ବା ଉପାଦାନ ମଧ୍ୟରେ ଥ‌ିବା ରୈଖିକ ସହ ସଂପର୍କ ସମୟରେ ସମ୍ଭବ ହୋଇଥାଏ ।

ମାତ୍ର ଏହି ଶୈଖିକ ସଂପର୍କ କେତେକ କ୍ଷେତ୍ରରେ ଦୃଷ୍ଟିଗୋଚର ହେଉଥ୍ଲେହେଁ କେତେକ ବାସ୍ତବ କ୍ଷେତ୍ରରେ ଏହା ଦେଖାଯାଇ ନଥାଏ । ଯଥା ଗଣନସଂଖ୍ୟା ଏବଂ ସେମାନଙ୍କର ବର୍ଗମାଳା କ୍ଷେତ୍ରରେ ରୈଖିକ ସଂପର୍କ ରହିଥିଲା ବେଳେ ଚାହିଦା ଓ ଦ୍ରବ୍ୟର ଦାମ୍ କ୍ଷେତ୍ରରେ ସେପରି ସଂପର୍କ ଦେଖାଯାଏ ନାହିଁ । କାରଣ ଦ୍ରବ୍ୟର ଦାମ୍‌ର ପରିବର୍ତ୍ତନ ଓ ତଦ୍ଵଜନିତ ଚାହିଦା ପରିମାଣର ପରିବର୍ତ୍ତନ ଏକ ସ୍ଥିର ଅନୁପାତରେ ଘଟି ନ ଥାଏ ।

ପୂର୍ଣ୍ଣ ସହସଂପର୍କ – (Perfect correlation) – ଯଦି ଦୁଇଟି ରାଶି ବା ଉପାଦାନର ପରିବର୍ତ୍ତନ ଏକ ସ୍ଥିର ଅନୁପାତରେ ଘଟିଥାଏ ତାହାକୁ ପୂର୍ଣ୍ଣ ସହସଂପର୍କ କୁହାଯାଏ । ପୂର୍ଣ୍ଣ ସହସଂପର୍କ କ୍ଷେତ୍ରରେ ଗୋଟିଏ ରାଶି ବା ଉପାଦାନର ହ୍ରାସ ବା ବୃଦ୍ଧି ସହ ଅନ୍ୟ ରାଶିର ହ୍ରାସ ବା ବୃଦ୍ଧି ମଧ୍ୟରେ ଏକ ସ୍ଥିର ଅନୁପାତ ବଜାୟ ରହିଥାଏ । ଅର୍ଥାତ୍ ଦୁଇଟି ରାଶି ମଧ୍ୟରେ ଆନୁପାତିକ ପରିବର୍ତ୍ତନ ସ୍ଥିର ରହିଥାଏ ।

ଏହି ପୂର୍ଣ୍ଣ ସହସଂପର୍କ ଯୋଗାତ୍ମକ (Positive) ବା ଋଣାତ୍ମକ (Negative) ହୋଇପାରେ । ଯଦି ଦୁଇଟି ରାଶି ବା ଉପାଦାନର ମାଳା ଏକ ଆନୁପାତିକ ହାରରେ ସମଦିଗରେ ପରିବର୍ତ୍ତନ ହୁଅନ୍ତି ତେବେ ତାହାକୁ ଯୋଗାତ୍ମକ ପୂର୍ଣ ସହସଂପର୍କ କୁହାଯାଏ ଓ ଅନ୍ୟପକ୍ଷରେ ଯଦି ଏହି ଦୁଇଟି ରାଶିର ମାଳା ଆନୁପାତିକ ହାରରେ ପରସ୍ପର ବିପରୀତ ମୁଖୀ ହୁଅନ୍ତି ତାହାକୁ ଋଣାତ୍ମକ ପୂର୍ଣ୍ଣ ସହସଂପର୍କ କୁହାଯାଏ ।

ଅର୍ଥନୈତିକ ପ୍ରକ୍ରିୟାରେ ଏହି ଦୁଇ ପ୍ରକାର ସଂପର୍କ କ୍ଵଚିତ୍ ଦେଖାଯାଏ କାରଣ ଦୁଇଟି ମାଳାର ରାଶିଦ୍ଵୟ ପରସ୍ପର ପୂର୍ଣ ନିର୍ଭରଶୀଳ ହୋଇନଥାନ୍ତି ।

ତେଣୁ ଏହି ପରିସ୍ଥିତିରେ ସହସଂପର୍କର ମାତ୍ରାର ପରିମାଣାତ୍ମକ ପରିପ୍ରକାଶର ଆବଶ୍ୟକତା ପଡ଼ିଥାଏ । ଏକ ଉପଯୁକ୍ତ ପରିମାପକ ସାହାଯ୍ୟରେ ଦୁଇଟି ମାଳାର ରାଶିଦ୍ଵୟ ମଧ୍ଯରେ ରହିଥ‌ିବା ପାରସ୍ପରିକ ସଂପର୍କ ପରିମାଣାତ୍ମକ ପରିପ୍ରକାଶ କରାଯିବାର ଆବଶ୍ୟକତା ରହିଥାଏ ।

ଏ କ୍ଷେତ୍ରରେ ସହସଂପର୍କର ଗୁଣାଙ୍କ ଏକ ଉପଯୁକ୍ତ ପରିମାପକ ଭାବରେ ଗ୍ରହଣ କରାଯାଏ । ତେଣୁ ସହ ସଂପର୍କ ଗୁଣାଙ୍କ ଦୁଇଟି ମାଳାରେ ରହିଥ‌ିବା ରାଶିମାନଙ୍କ ମଧ୍ୟରେ ରହିଥ‌ିବା ସଂପର୍କର ମାତ୍ରାର ପରିମାଣାତ୍ମକ ପରିପ୍ରକାଶ କରିଥାଏ । ଏହି ପରିମାଣାତ୍ମକ ମାତ୍ରାରୁ ରାଶିଦ୍ଵୟ ମଧ୍ୟରେ ରହିଥ‌ିବା ସଂପର୍କ ବିଷୟରେ ସିଦ୍ଧାନ୍ତ ନିଆଯାଇପାରେ ।

ଏହି ସହସଂପର୍କ ଗୁଣାଙ୍କର ମୂଲ୍ୟ +1 ରୁ –1 ମଧ୍ୟରେ ସୀମିତ ରହିଥାଏ । ପୂର୍ଣ୍ଣ ଯୋଗାତ୍ମକ ସଂପର୍କ କ୍ଷେତ୍ରରେ ଏହାର ମୂଲ୍ୟ +1 ହୋଇଥିବାବେଳେ ପୂର୍ଣ ଋଣାତ୍ମକ ସହସଂପର୍କ କ୍ଷେତ୍ରରେ ଏହାର ମୂଲ୍ୟ – ହୋଇଥାଏ । ଏହି ଦୁଇଟି ଚରମ ମୂଲ୍ୟର ମଧ୍ୟ ବିନ୍ଦୁର ମୂଲ୍ୟ ‘0’ ହୋଇଥାଏ ଯାହା ସହସଂପର୍କର ଅନୁପସ୍ଥିତି ଦର୍ଶାଇଥାଏ । ଏହି ସହସଂପର୍କ ଗୁଣାଙ୍କ କୁ ଇଂରାଜୀ ଅକ୍ଷର ‘r’ ମାଧ୍ୟମରେ ଚିହ୍ନିତ କରାଯାଇଥାଏ ।

କାର୍ଲ ପିଅରସନ ଏକ ଗାଣିତିକ ପଦ୍ଧତି ଅବଲମ୍ବନ କରିଥିଲେ ଯାହା କାଇଁ ପିଅରସନଙ୍କ ସହସଂପର୍କ ଗୁଣାଙ୍କ ନାମରେ ପରିଚିତ । କାର୍ଲ ପିଅରସନଙ୍କ ଦ୍ଵାରା ପ୍ରଣୀତ ଏହି ଗୁଣାଙ୍କ ସହାଯ୍ୟରେ ସହସଂପର୍କର ପରିମାଣାତ୍ମକ ମାତ୍ରା ସହଜରେ ନିର୍ଦ୍ଧାରଣ
କରାଯାଇପାରିଥାଏ । ‘r’ ଦ୍ୱାରା ଚିହ୍ନିତ ଏହି ଗୁଣାଙ୍କ ସହସଂପର୍କର ମାତ୍ରା ପରିପ୍ରକାଶର ଏକ ସରଳ ତଥା ଉପଯୁକ୍ତ ପରିମାପକ ।
\(\mathrm{r}=\frac{\Sigma(\mathrm{x}-\overline{\mathrm{x}})(\mathrm{y}-\overline{\mathrm{y}})}{\text { N. } \sigma_{\mathrm{x}} \sigma_{\mathrm{y}}}\)

ଏଠାରେ = x ଓ y ଦୁଇଟି ମାଳାରେ ଥ‌ିବା ରାଶିଦ୍ଧୟର ଲବ୍‌ଧାଙ୍କ
x̄ → x ରାଶିମାନଙ୍କର ମାଧ୍ଯମାନ ।
ȳ → y ରାଶିମାନଙ୍କର ମାଧ୍ଯମାନ
N → x ଓ y ରାଶି ଦ୍ବୟର କ୍ରମିକ ଯୋଡ଼ି ସଂଖ୍ୟା ।
σ_x → x ରାଶି ମଧ୍ୟରେ ଥିବା ମାନକ ବିଚ୍ୟୁତି ।
σ_y → y ରାଶି ମଧ୍ୟରେ ଥ‌ିବା ମାନକ ବିଚ୍ୟୁତି ।

ଏହି ପଦ୍ଧତି ଅବଲମ୍ବନରେ 1 ର ମୂଲ୍ୟ +1 ହେଲେ, ଏହା ପୂର୍ବ ଯୋଗାତ୍ମକ ସହସଂପର୍କ ଦର୍ଶାଇଥାଏ, r ର ମୂଲ୍ୟ – ହେଲେ ଏହା ପୂର୍ଣ୍ଣ ଋଣାତ୍ମକ ସହ ସଂପର୍କ ସୂଚାଇଥାଏ ଏବଂ r ର ମୂଲ୍ୟ ( ହେଲେ ଏହା କୌଣସି ସହସଂପର୍କ ଦର୍ଶାଇ ନଥାଏ । କାର୍ଲ ପିଅରସନଙ୍କ ଏହି ଗୁଣାଙ୍କ ରାଶିଦ୍ଵୟ ମଧ୍ୟରେ ରହିଥିବା ପାରସ୍ପରିକ ସଂପର୍କର ମାତ୍ରା ପରିପ୍ରକାଶ ନିମନ୍ତେ ଏକ ଉପଯୁକ୍ତ ତଥା ନିର୍ଭରଯୋଗ୍ୟ ପରିମାପକ ଭାବରେ ଗ୍ରହଣ କରାଯାଇଥାଏ ।

୪। ସହସମ୍ବନ୍ଧ କ’ଣ ? ଅର୍ଥଶାସ୍ତ୍ରରେ ସହସମ୍ବନ୍ଧର ବ୍ୟବହାର କ’ଣ ଆଲୋଚନା କର ।
Answer:
ଅର୍ଥନୈତିକ ଚଳମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ଓ ଆଚରଣକୁ ବୁଝିବାରେ ସହସମ୍ବନ୍ଧ ବିଶ୍ଳେଷଣ ସହାୟତା କରେ । ଅର୍ଥନୈତିକ ସ୍ଥିରତା ପାଇଁ ଅର୍ଥନୀତିଜ୍ଞମାନଙ୍କୁ ଅସ୍ଥିରତା ସୃଷ୍ଟି କରୁଛି । କାରଣଗୁଡ଼ିକ ନିରୂପଣ କରିବାରେ ସହାୟତା କରେ, ସହସମ୍ବନ୍ଧ ବ୍ୟବସାୟ, ବାଣିଜ୍ୟ, ଶିଳ୍ପ, ପରିବେଶ ଆଦି ଅନେକ ଅର୍ଥନୈତିକ କ୍ଷେତ୍ରରେ ବହୁଳଭାବେ ବ୍ୟବହୃତ ହୁଏ । ତେବେ ଏହି ପରିସଂଖ୍ୟାନ ପଦ୍ଧତିର ଅର୍ଥନୀତିରେ ବିଶେଷ ବ୍ୟବହାର ବିଷୟରେ ନିମ୍ନରେ ଆଲୋଚନା କରାଯାଇଛି ।

(a) ସମ୍ପର୍କର ପରିସଂଖ୍ୟାନ ଗୁରୁତ୍ଵ ପରୀକ୍ଷା – ବିଭିନ୍ନ ଚଳ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ପାଇଁ ସହସମ୍ବନ୍ଧରେ ସାହାଯ୍ୟ ନିଆଯାଇଥାଏ । ଯେପରି ଦାମ୍ ଓ ଯୋଗାଣ ମଧ୍ୟରେ ଥିବା ବିଭିନ୍ନ ଚଳ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ପାଇଁ ସହସମ୍ବନ୍ଧରେ ସାହାଯ୍ୟ ସମ୍ପର୍କର ପରିମାଣ ଭାବରେ ସହସମ୍ବନ୍ଧର ଗୁଣାଙ୍କ (r)କୁ ‘t’ test ଦ୍ଵାରା ପରୀକ୍ଷା କରାଯାଏ ।

(b) ଚଳମାନଙ୍କ ମଧ୍ୟରେ ସମ୍ବନ୍ଧ – ସହସମ୍ବନ୍ଧର ଗୁଣାଙ୍କଦ୍ବାରା ଦୁଇଟି ଚଳମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ଋଣାତ୍ମକ ଏବଂ ଯୁକ୍ତାତ୍ମକ ସମ୍ବନ୍ଧ ମାପିବା ସହିତ ସମ୍ବନ୍ଧର ଗଭୀରତା ମଧ୍ୟ ପରିମାପ କରିହୁଏ । ଅର୍ଥଶାସ୍ତ୍ର, ବ୍ୟବସାୟ, ବାଣିଜ୍ୟ ଏବଂ ବିଜ୍ଞାନ କ୍ଷେତ୍ରରେ ଥିବା ଚଳମାନଙ୍କ ମଧ୍ୟରେ ସମ୍ବନ୍ଧ ମାପିବାରେ ସହସମ୍ବନ୍ଧ ପଦ୍ଧତି ଅନୁସରଣ କରାଯାଏ ।

(c) ଯୋଜନା ପ୍ରସ୍ତୁତ ଓ ପ୍ରଣୟନ – ନୀତି ପ୍ରସ୍ତୁତ ଓ ପ୍ରଣୟନ ନିମନ୍ତେ ସଂଶ୍ଳିଷ୍ଟ ବିଭିନ୍ନ ଉପାଦାନ ମଧ୍ୟରେ ସହସମ୍ବନ୍ଧ ପଦ୍ଧତି ବ୍ୟବହାର କରାଯାଏ । ଯଦି ସରକାର ଟିକସହାର ବୃଦ୍ଧି କରନ୍ତି, ତେବେ ତାହାର ନୀତି ପ୍ରଣୟନ ପୂର୍ବରୁ ମୁଣ୍ଡପିଛା ଆୟ ଓ ଜନସାଧାରଣଙ୍କ ଟିକସ ସେବାର କ୍ଷମତା ସହିତ ତାହାର ସମ୍ପର୍କ ଏହି ପଦ୍ଧତି ମାଧ୍ୟମରେ ପରୀକ୍ଷା କରାଯାଏ ।

(d) ଗବେଷଣା – ଆଧୁନିକ ବିଜ୍ଞାନ ଯୁଗରେ ଅର୍ଥନୀତି ବ୍ୟତୀତ ଯେତେସବୁ କ୍ଷେତ୍ର; ଯଥା – ଶିକ୍ଷା, ସ୍ୱାସ୍ଥ୍ୟ, ପରିବେଶ, ସମାଜ ଆଦି ଗବେଷଣା କ୍ଷେତ୍ରର ସହସମ୍ବନ୍ଧର ବିଶେଷ ବ୍ୟବହାର ହୁଏ ।

୫। ସମାଶ୍ରୟଣ କହିଲେ କ’ଣ ବୁଝ ? ଏହି ପଦ୍ଧତିର ଅର୍ଥନୀତିରେ ବ୍ୟବହାର ବୁଝାଇ ଲେଖ ।
Answer:
ସମାଶ୍ରୟଣ କହିଲେ ଦୁଇଟି ଚଳ ମଧ୍ଯରେ ହାରାହାରି ସମ୍ପର୍କକୁ ବୁଝାଏ । ଏହା ବିଭିନ୍ନ କ୍ଷେତ୍ରରେ ଭବିଷ୍ୟ ଆକଳନ କରିବାରେ ସହାୟକ ହୋଇଥାଏ । 1877 ମସିହାରେ ପ୍ରଥମେ ସାର୍ ପ୍ରାନ୍ସିସ୍ ଗାଲ୍ଟନ୍ ଚଳ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ପରିମାପ ଓ ବିଶ୍ଳେଷଣ କରିବାରେ ପ୍ରୟୋଗ କରିଥିଲେ । ଯଦି ଗୋଟିଏ ଚଳର ମୂଲ୍ୟ ଜଣାଥାଏ, ତେବେ ଅନ୍ୟ ଚଳର ମୂଲ୍ୟ ସମାଶ୍ରୟଣଦ୍ୱାରା କଳନା କରିହୁଏ ।

ଯେପରି ବଜାରରେ କୌଣସି ଦ୍ରବ୍ୟର ଦାମ୍ ଜଣାଥିଲେ ଏହାର ଯୋଗାଣର ପରିମାଣ ଜାଣିହୁଏ । ଯଉଁ ଚଳର ଭବିଷ୍ୟତ କଳନା କରାଯାଏ ତାକୁ ନିର୍ଭରଶୀଳ ଚଳ (y) ଏବଂ ଯେଉଁ ଚଳଦ୍ଵାରା ଭବିଷ୍ୟ କଳନା କରାଯାଏ, ତାହାକୁ ସ୍ୱାଧୀନ ଚଳ (x) କୁହାଯାଏ । ସମାଶ୍ରୟଣ ସମୀକରଣକୁ y = a + bx ଦ୍ବାରା ଲେଖାଯାଏ ।

ତେବେ ସଂକ୍ଷେପରେ କହିଲେ ସମାଶ୍ରୟଣର ମୁଖ୍ୟ ଉଦ୍ଦେଶ୍ୟ ହେଲା ସ୍ଵାଧୀନ ଚଳ ଏବଂ ନିର୍ଭରଶୀଳ ଚଳ ମଧ୍ୟରେ କାର୍ଯ୍ୟକାରୀ ସମ୍ପର୍କ ସ୍ଥାପନ କରିବା, ଯାହାଦ୍ଵାରା ପୂର୍ବତନ ଚଳର ପରିବର୍ତ୍ତନରେ ଭବିଷ୍ୟତର ଅବସ୍ଥାକୁ ଆକଳନ କରିବ । ଯେହେତୁ ସମାଶ୍ରୟଣ ବିଶ୍ଳେଷଣଦ୍ଵାରା ଚଳମାନଙ୍କର ବ୍ୟବହାରୀକ ସମ୍ପର୍କକୁ ଜଣାଯାଏ, ତେଣୁ ଅନ୍ୟାନ୍ୟ ବିଷୟ ଭଳି ଅର୍ଥଶାସ୍ତ୍ର ଅଧ୍ୟୟନ କ୍ଷେତ୍ରରେ ବିଶେଷ ସହାୟକ ହୋଇଥାଏ । ଉଦାହରଣସ୍ୱରୂପ ଉପଭୋଗ ଫଳନ ରେଖା ଅଙ୍କନ କଲାବେଳେ ଆମେ ସମାଶ୍ରୟଣ ବିଶ୍ଳେଷଣରେ ଦୁଇଟି ଚଳ ବିଷୟରେ ଆଲୋଚନା କରୁ ।

ଆୟ ଯାହା ହେଲା ସ୍ଵାଧୀନ ଚଳ ଏବଂ ଉପଭୋଗ ନିର୍ଭରଶୀଳ ଚଳ । ପ୍ରସିଦ୍ଧ ଅର୍ଥନୀତିଜ୍ଞ ତାଙ୍କ ଆୟର ସାଧାରଣ ତତ୍ତ୍ବ କ୍ଷେତ୍ରରେ ପରିସଂଖ୍ୟାନ ମାଧ୍ୟମରେ ସିଦ୍ଧାନ୍ତରେ ପହଞ୍ଚି ପାରି ଅର୍ଥଶାସ୍ତ୍ରର ଗବେଷଣା କ୍ଷେତ୍ରରେ ସମାଶ୍ରୟଣଦ୍ୱାରା ଆକଳନ ହୋଇଥାଏ । ତେବେ ନିମ୍ନରେ ଅର୍ଥନୀତିରେ ଏହାର ବ୍ୟବହାର ବିଷୟରେ ଆଲୋଚନା କରାଯାଇଛି ।

(i) ସମ୍ପର୍କର ଆକଳନ ବା ହିସାବ – କୌଣସି ଅର୍ଥନୈତିକ ଚଳ ମଧ୍ୟରେ ଥିବା ପ୍ରଭାବ ଓ ସମ୍ପର୍କ ଆକଳନ କରିବା ପାଇଁ ସମାଶ୍ରୟଣ ଏକ ପ୍ରାଥମିକ ପଦ୍ଧତି, ଉଦାହରଣସ୍ୱରୂପ ପୁଞ୍ଜିର ପରିମାଣ ବୃଦ୍ଧିପାଇଲେ ସମାଶ୍ରୟଣଦ୍ୱାରା ଏହାର ଉତ୍ପାଦନ ଉପରେ ପଡ଼ୁଥ‌ିବା ପ୍ରଭାବର ପରିମାପ କରିହୁଏ ଏବଂ ବିଶ୍ଳେଷଣ ମଧ୍ୟ କରିହୁଏ ।

(ii) ଭବିଷ୍ୟତ କଳନା କରିବା – ସମାଶ୍ରୟଣ ମାଧ୍ୟମରେ ସ୍ବାଧୀନ ଚଳର ମୂଲ୍ୟଦ୍ଵାରା ନିର୍ଭରଶୀଳ ଚଳର ଭବିଷ୍ୟତ କଳନା କରାଯାଏ । ପେଟ୍ରୋଲର ଦାମ୍ ବଢ଼ିଲେ ସ୍କୁଟରର ମୂଲ୍ୟ କେତେ ବଢ଼ିବ ବା କମିବ ତାହା ସମାଶ୍ରୟଣର ବିଶ୍ଳେଷଣଦ୍ୱାରା

(iii) ସହସମ୍ପର୍କ – ଦୁଇଟି ସମାଶ୍ରୟଣର ଗୁଣାଙ୍କ ଜଣାଥିଲେ ତ’ର ଗୁଣଫଳର ବର୍ଗମୂଳ ବାହର କଲେ ସହସମ୍ପର୍କର ଗୁଣାଙ୍କ ନିର୍ଣ୍ଣୟ ହୁଏ ।
ଏତଦ୍ ବ୍ୟତୀତ ସମାଶ୍ରୟଣ ପଦ୍ଧତିଦ୍ୱାରା ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟାବଳୀର ଅଧିକାଂଶ କ୍ଷେତ୍ରରେ ବ୍ୟବହୃତ ହୋଇଥାଏ ।