CHSE Odisha Class 11 Economics Solutions Unit 7 ପରିସାଂଖ୍ୟିକ ପଦ୍ଧତି (I)

Odisha State Board CHSE Odisha Class 11 Economics Solutions Unit 7 ପରିସାଂଖ୍ୟିକ ପଦ୍ଧତି (I) Questions and Answers.

CHSE Odisha 11th Class Economics Unit 7 Question Answer ପରିସାଂଖ୍ୟିକ ପଦ୍ଧତି (I)

I. ନିମ୍ନୋକ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ପ୍ରଦତ୍ତ ବିକଳ୍ପଗୁଡ଼ିକ ମଧ୍ୟରୁ ଚୟନ କର।
[Choose the Correct answer of the following from the Alternatives as given]

Question ୧।.
+3 ଦ୍ଵିତୀୟ ବର୍ଷର୍ 50 ଜଣ ଛାତ୍ରଙ୍କର ଅର୍ଥନୀତିରେ ହାରାହାରି ନମ୍ବର(ମାଧ୍ୟମାନ) 40 ଓ 60। ଜଣ ଛାତ୍ରୀଙ୍କର ଅର୍ଥନୀତିରେ ହାରାହାରି ନମ୍ବର (ମାଧ୍ୟମାନ) 30। ତେବେ ମୋଟ 110 ଜଣ ଛାତ୍ର-ଛାତ୍ରୀଙ୍କର ମିଳିତ ମାଧ୍ଯମାନ ବା ହାରାହାରୀ ମୂଲ୍ୟ କେତେ ହେବ ?
(A) 34,54
(C) 54.23
(B) 15.64
(D) 32.28
Answer:
(A) 34,54

Question ୨।
ମଧ୍ୟମାକୁ କେଉଁ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପକ କୁହାଯାଏ ?
(A) ଅବସ୍ଥାପିତ
(B) ଗାଣିତିକ
(C) ଉଭୟ (A) ଓ (B)
(D) ଉପରୋକ୍ତ କୌଣସିଟି
Answer:
(A) ମାଧ୍ଯମାନ

Question ୩।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁ ହାରାହାରିର ମୂଲ୍ୟକୁ ରେଖାଚିତ୍ର ସାହାଯ୍ୟରେ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରିବ ?
(A) ଗରିଷ୍ଠକ
(B) ମାଧ୍ଯମାନ
(C) ମଧ୍ଯମା
(D) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(A) ଗରିଷ୍ଠକ

Question ୪।
ସବୁଠାରୁ ଅଧ‌ିକ ଥର ଥୁବା ଲବ୍‌ଧାକଙ୍କୁ କ’ଣ କୁହାଯାଏ ?
(A) ଚାରିଷ୍ଟକ
(B) ମାଧ୍ୟମାନ
(C) ମଧ୍ୟମା
(D) ଉପରେ।କ୍ତ ସମସ୍ତ
Answer:
(D) ଉପରେ।କ୍ତ ସମସ୍ତ

Question ୫।
ଗୋଟିଏ ବାରମ୍ବାରତା ବିତରଣର କଚ୍ଛିତ ମାଧ୍ଯମାନର ମୂଲ୍ୟ 350, ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ସଂଖ୍ୟା 0 ଏବଂ ଲବ୍‌ଧାଙ୍କରୁ କଳ୍ପିତ ମାଧ୍ଯମାନର ବିଚ୍ୟୁତିଗୁନିକର ସମଷ୍ଟି 100), ତେବେ ମାଧ୍ଯମାନର ମୂଲ୍ୟ କେତେ ?
(A) 366.60
(B) 140.50
(C) 282.60
(D) 351.66
Answer:
(D) 351.66

Question ୬।
x : 10, 12, 18, 11, 10, 10, 10, 15, 10 । ଏହି ବାରମ୍ବାରତାର ବିତରଣର ଗରିଷ୍ଠକର ମୂଲ୍ୟ କେତେ ?
(A) 10
(B) 12
(C) 18
(D) 11
Answer:
(A) 10

Question ୭।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ମାଧ୍ଯମାନର ସୁଗୁଣ ?
(A) ସହଜରେ ହୃଦୟଙ୍ଗମ କରିହୁଏ
(B) ସରଳ ପଦ୍ଧତି
(C) ଲରେଞ୍ଜ ବକ୍ରରେଖା
(D) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(D) ଉପରୋକ୍ତ ସମସ୍ତ

Question ୮।
Σ(x – x̄) =?
(A) 1
(B) 0
(C) 15
(D) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(B) 0

Question ୯।
ମଧ୍ୟମା ତଥ୍ୟାବଳୀକୁ କେତେ ଅଂଶରେ ବିଭକ୍ତ କରେ?
(A) 2
(B) 1
(C) 4
(D) 6
Answer:
(A) 2

Question ୧୦।
ମଧ୍ଯମାରୁ ରେଖାଚିତ୍ର ଉପସ୍ଥାପନକୁ କ’ଣ କୁହାଯାଏ ?
(A) ଓଜିଡ୍
(B) ହିଷ୍ଟାଗ୍ରାମ୍
(C) ଲରେଞ୍ଜ ଚକ୍ରରେଖା
(D) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(A) ଓଜିଡ୍

Question ୧୧।
ଯଦି ପାଞ୍ଚଜଣ ବ୍ୟକ୍ତିଙ୍କର ମାସିକ ଦରମା ଯଥାକ୍ରମେ Rs. 6000, Rs.8500, Rs.7500, Rs. 12000 ଏବଂ Rs. 15000 ହୁଏ, ତେବେ ସେମାନଙ୍କର ହାରାହାରି ଦରମା (ମାଧ୍ଯମାନ) କେତେ ହେବ ?
(A) 9700
(B) 7000
(C) 6800
(D) 12000
Answer:
(C) 6800

Question ୧୨।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ମଧ୍ଯମାର ସୁଗୁଣ ?
(A) ଗଣନା ସରଳ
(B) ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଜ୍ଞା ଅଛି
(C) ଲେଖଚିତ୍ର ମାଧ୍ୟମରେ ଉପସ୍ଥାପନ କରାଯାଇପାରେ
(D) ଉପରୋକ୍ତ ସମୟ
Answer:
(D) ଉପରୋକ୍ତ ସମୟ

Question ୧୩ ।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଚତୁର୍ଥାଂଶ ବିଚ୍ୟୁତିର ଦୁର୍ଗୁଣ ?
(A) ରାଶିମାଳାର 50% ପର୍ଯ୍ୟବେକ୍ଷଣକୁ ବିଚାରକୁ ନିଏ।
(B) ଯୁକ୍ତ ସମ୍ଭାଗଯୁକ୍ତ ବିତରଣରେ ବିଚ୍ୟୁତି ନିର୍ୟକର କରାଯାଇପାରେ।
(C) ଚୟନ ଅସ୍ଥିରତା ଦ୍ଵାରା ପ୍ରଭାବିତ ହୁଏ।
(D) ଉପରୋକ୍ତ ସମସ୍ତ।
Answer:
(A) ରାଶିମାଳାର 50% ପର୍ଯ୍ୟବେକ୍ଷଣକୁ ବିଚାରକୁ ନିଏ।

Question ୧୪ ।
ଚତୁର୍ଥାଂଶ ବିଚ୍ୟୁତି ଗୋଟିଏ ବାରମ୍ବାରତା ବିତରଣକୁ କେତେ ଭାଗରେ ବିଭକ୍ତ କରେ ?
(A) 2
(B) 4
(C) 8
(D) 5
Answer:
(A) 2

Question ୧୫।
ମାଧ୍ୟ ବିଦ୍ୟୁତିର ମୂଲ୍ୟ ନିମ୍ନଲିଖତ କେଉଁ ହାରାହାରିକୁ ନିର୍ଦ୍ଧାରଣ କରାଯାଏ ?
(A) ମାଧ୍ଯମାନ
(B) ମାଧ୍ଯମା
(C) ଜ୍ୟାମିତିକ ମାଧ୍ୟମାନ
(D) ଉଭୟ (A) ଓ (B)
Answer:
(D) ଉଭୟ (A) ଓ (B)

Question ୧୬।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ମାଧ୍ୟ ବିଦ୍ୟୁତିର ସୁଗୁଣ ?
(A) ସଠିକ୍ ସଂଜ୍ଞା ଅଛି
(B) ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ଆଧାରିତ
(C) ଚରମ ଲବ୍‌ଧାଙ୍କ ଦ୍ବାରା କମ୍ ପ୍ରଭାବିତ
(D) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(D) ଉପରୋକ୍ତ ସମସ୍ତ

Question ୧୭।
X : 10, 12, 14, 16, 18 ର ମାଧ୍ୟ ବିଚ୍ୟୁତିର ମୂଲ୍ୟ କେତେ ?
(A) 2.4
(B) 5
(C) 4
(D) 3
Answer:
(A) 2.4

Question ୧୮।
ମାନକ ବିଚ୍ୟୁତିର ବର୍ଗକୁ କ’ଣ କୁହାଯାଏ ?
(A) ପ୍ରସାରଣ
(B) ବିଚରଣ ଗୁଣାଙ୍କ
(C) ମାଧ୍ୟବିଚ୍ୟୁତି
(D) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(A) ପ୍ରସାରଣ

Question ୧୯।
ମାଧ୍ୟ ବିଚ୍ୟୁତି ଓ ମାଧ୍ଯମାନର ଶତକଡ଼ା ଅନୁପାତକୁ କ’ଣ କୁହାଯାଏ ?
(A) ପ୍ରସାରଣ
(B) ବିଚରଣ ଗୁଣାଙ୍କ
(C) ମାନଙ୍କ ବିଚ୍ୟୁତି
(D) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(B) ବିଚରଣ ଗୁଣାଙ୍କ

Question ୨୦।
ନିମ୍ନଲିଖୁତ ମଧ୍ୟରୁ କେଉଁଟି ମାନକ ବିଦ୍ୟୁତିର ସୁଗୁଣ ?
(A) ଅଭିକଳନା ସହଜ ନୁହେଁ
(B) ଚରମ ଲବ୍‌ଧାଙ୍କ ଦ୍ଵାରା ପ୍ରଭାବିତ
(C) ଏହାର ସଠିକ୍ ସଂଜ୍ଞା ଅଛି
(D) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(C) ଏହାର ସଠିକ୍ ସଂଜ୍ଞା ଅଛି

Question ୨୧।
\(\frac{6}{\bar{x}}\) 100 କେଉଁ ବିଚ୍ଛୁରଣ ମାପକର ପଦ୍ଧତି ?
(A) ମାଧ୍ଯମାନ
(B) ବିଚରଣ ଗୁଣାଙ୍କ ବା ପରିବର୍ତ୍ତନୀୟ ଗୁଣାଙ୍କ(c.v)
(C) ପ୍ରସାରଣ
(D) ମଧ୍ୟମା
Answer:
(B) ବିଚରଣ ଗୁଣାଙ୍କ ବା ପରିବର୍ତ୍ତନୀୟ ଗୁଣାଙ୍କ(c.v)

Question ୨୨।
ମାନକ ବିଦ୍ୟୁତିର ରେଖାଙ୍କିତ ଉପସ୍ଥାପନ
(A) ଓଜିଭ୍
(B) ବିଚରଣ ଗୁଣାଙ୍କ
(C) ହିଷ୍ଟାଗ୍ରାମ
(D) ସମସ୍ତଟି
Answer:
(B) ବିଚରଣ ଗୁଣାଙ୍କ

Question ୨୩।
ମୁକ୍ତ ସଂଭାଗ ଶ୍ରେଣୀ କ୍ଷେତ୍ରରେ ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ :
(A) ମଧ୍ୟମା
(B) ମାଧ୍ଯମାନ
(C) ଗରିଷ୍ଠକ
(D) ସମସ୍ତଟି
Answer:
(A) ମଧ୍ୟମା

Question ୨୪।
ଲୋରେଞ୍ଜ ବକ୍ର କିଏ ଉତ୍ପତ୍ତି କରିଥିଲେ ?
(A) ମାକ୍ସ ଓ ଲୋରେଞ୍ଜ
(B) ମାର୍ନାଲ୍
(C) ପିଗୁ
(D) ସମସ୍ତଟି ନୁହେଁ
Answer:
(A) ମାକ୍ସ ଓ ଲୋରେଞ୍ଜ

Question ୨୫।
ଯଦି X ର ମୂଲ୍ୟ ୨୦-୩୦, ୩୦-୪୦, ୪୦-୫୦ ଓ ୫୦-୬୦ ଶ୍ରେଣୀର ବିସ୍ତାର ମୂଲ୍ୟ କେତେ ?
(A) ୪୦
(B) ୨୦
(C) ୩୦ .
(D) ୬୦
Answer:
(A) ୪୦

Question ୨୬।
ଯଦି, X = 10,12, 14, 16, 18, 20 ହୁଏ, ତେବେ ମଧ୍ୟମାର ମୂଲ୍ୟ କେତେ ହେବ ?
(A) 15
(B) 14
(C) 16
(D) 20
Answer:
(A) 15

Question ୨୭।
ବିଜୁରଣର ଆପେକ୍ଷିକ ପରିମାପକ
(A) ବିସ୍ତାର
(B) ମାନକ ବିଚ୍ୟୁତି
(C) ମାଧ୍ୟ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ
(D) ସମସ୍ତଟି
Answer:
(C) ମାଧ୍ୟ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ

Question ୨୮।
\(\Sigma(\mathbf{X}-\overline{\mathbf{X}})^2\)
(A) ସର୍ବନିମ୍ନ
(B) ଶୂନ୍ଯ
(C) ସର୍ବାଧକ
(D) ସମସ୍ତ
Answer:
(A) ସର୍ବନିମ୍ନ

Question ୨୯।
ଗୁଣାଙ୍କର ମୂଲ୍ୟ ସର୍ବଦା :
(A) ୧ ରୁ ଅଧିକ
(B) ୧ ରୁ କମ୍
(C) ୧
(D) ସମସ୍ତଟି
Answer:
(B) ୧ ରୁ କମ୍

II. ନିମ୍ନୋକ୍ତ ଉକ୍ତିଗୁଡ଼ିକର ସଠିକତା ପ୍ରମାଣ କର। ଆବଶ୍ୟକ ସ୍ଥଳେ ରେଖାଙ୍କିତ ଅଂଶଗୁଡ଼ିକୁ ନ ବଦଳାଇ ଭ୍ରମ ସଂଶୋଧନ କର।
[Prove the correctness of the followings correct then if necessary with- out changing words underlined.]

Question ୧।
ମାଧ୍ଯମାନ ଏକ ଅବସ୍ଥାପିତ ହାରାହାରି।
Answer:
ମାଧ୍ଯମାନ ଏକ ଗାଣିତିକ ହାରାହାରି।

Question ୨।
ମଧର୍ମା ଏକ ଅବସ୍ଥାପିତ ହାରାହାରି।
Answer:
ସଠିକ୍।

Question ୩।
ମାଧ୍ୟମାନର ମୂଲ୍ୟକୁ ରେଖାଚିତ୍ର ସାହାଯ୍ୟରେ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ।
Answer:
ମଧ୍ଯମାର ମୂଲ୍ୟକୁ ରେଖାଚିତ୍ର ସାହାଯ୍ୟରେ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ।

Question ୪।
3 Median – 2 Mean = Mode (ଗରିଷ୍ଠକ)
Answer:
ସଠିକ୍

Question ୫।
ମାଧ୍ଯମାନ ଚରମ ଲବ୍‌ଧାଙ୍କ ଦ୍ବାରା ପ୍ରଭାବିତ ହୁଏ।
Answer:
ସଠିକ୍

Question ୬।
ଗରିଷ୍ଠକର ସଠିକ୍ ସଂଜ୍ଞା ନାହିଁ।
Answer:
ସଠିକ୍

Question ୭।
ରେଖାଚିତ୍ର ମାଧ୍ୟମରେ ଗରିଷ୍ଠକର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ।
Answer:
ସଠିକ୍

Question ୮।
ଏକ ପ୍ରତିସମ ବଣ୍ଟନାରେ ମାଧ୍ଯମାନ ± ମଧ୍ୟମା ± ଗରିଷ୍ଠକ।
Answer:
ଏକ ପ୍ରତିଦସମ ବଣ୍ଟନରେ ମାଧମାନ = ମଧ୍ୟମା = ଗରିଷ୍ଠକ।

Question ୯।
ମାଧ୍ୟମାନ ପୂର୍ଣ୍ଣ ବୀଜଗଣିତ ପ୍ରୟୋଗ ନିମିତ୍ତ ଉପଯୁକ୍ତ।
Answer:
ସଠିକ୍

Question ୧୦।
ଗରିଷ୍ପକ ବଣ୍ଟନର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବେସିତ।
Answer:
ମାଧ୍ଯମାନ ବଣ୍ଟନର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବେସିତ।

Question ୧୧।
ବିସ୍ତାର ଚରମ ଲବ୍‌ଧାଙ୍କ ଦ୍ବାରା ବହୁ ପରିମାଣରେ ପ୍ରଭାବିତ ହୁଏ।
Answer:
ସଠିକ୍

Question ୧୨।
ଚତୁର୍ଥାଂଶ ଏକ ବାରମ୍ବାରତା ବିତରଣକୁ ଚାରି ଭାଗରେ ବିଭକ୍ତ କରିଥାଏ।
Answer:
ସଠିକ୍

Question ୧୩।
ମାନକ ବିଚ୍ୟୁତି ବିଜୁରଣର ଏକ ଗାଣିତିକ ପରିମାପକ।
Answer:
ସଠିକ୍

Question ୧୪।
ଯୁକ୍ତ ସଂଭାଗଯୁକ୍ତ ବିତରଣରେ ବିସ୍ତାର ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ।
Answer:
ଯୁକ୍ତ ସଂଭାଗଯୁକ୍ତ ବିତରଣରେ ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କରାଯାପାରେ।

Question ୧୫।
ମାଧ୍ୟ ବିଚ୍ୟୁତି (ସିଗ୍‌ମା) = \(\sqrt{\frac{\Sigma \mathrm{fdx}^2}{\Sigma \mathrm{f}}=\left(\frac{\Sigma \mathrm{fdx}}{\Sigma \mathrm{f}}\right)^2}\)
Answer:
ମାନକ ବିଚ୍ୟୁତି (ସିଗ୍‌ମା) = \(\sqrt{\frac{\Sigma \mathrm{fdx}^2}{\Sigma \mathrm{f}}=\left(\frac{\Sigma \mathrm{fdx}}{\Sigma \mathrm{f}}\right)^2}\)

Question ୧୬।
ମାନକ ବିଚ୍ୟୁତିର ସଠିକ୍ ସଂଜ୍ଞା ନାହିଁ।
Answer:
ମାନକ ବିଚ୍ୟୁତିର ସଠିକ୍ ସଂଜ୍ଞା ଅଛି।

Question ୧୭।
ମାଧ୍ୟ ବିଚ୍ୟୁତି ମଧ୍ୟମା କିମ୍ବା ମାଧ୍ୟମାନ ଠାରୁ ନିର୍ଣ୍ଣୟ କରାଯାଏ।
Answer:
ସଠିକ୍

Question ୧୮।
ମାନକ ବିଚ୍ୟୁତି ପୁନଃ ବୀଜଗାଣିତିକ ବିଶ୍ଳେଷଣ ଦ୍ବାରା ବ୍ୟବହାରକ୍ଷମ।
Answer:
ସଠିକ୍

Question ୧୯।
ବିବରଣ ଗୁଣାଙ୍କ ବିଚ୍ଛୁରଣ ମାପକର ଏକ ଆପେକ୍ଷିକ ପରିମାପକ।
Answer:
ସଠିକ୍

Question ୨୦।
ମାଧ୍ୟ ବିଚ୍ୟୁତି ବିଚ୍ଛୁରଣ ମାପକର ଏକ ଅବସ୍ଥାପିତ ପରିମାପକ।
Answer:
ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ବିଜୁରଣ ମାପକର ଏକ ଅବସ୍ଥାପିତ ପରିମାପକ।

III. ନିମ୍ନୋକ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇଟିରୁ ତିନୋଟି ବାକ୍ୟରେ ମଧ୍ୟରେ ଲେଖ।
[Answer the following questions within 2 to 3 sentences in each case.]

Question ୧।
ମଧ୍ୟମା (Median) କାହାକୁ କୁହାଯାଏ ?
Answer:
ମଧ୍ୟମା ଏକ ଅବସ୍ଥାପିତ ହାରାହାରି | କୌଣସି ତତ୍ୟାବଳୀର ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକ ଉଷ୍ଟକ୍ରମ ବା ଅଧଃକ୍ରମରେ ସଜାଡ଼ି ଦେଲେ ସେମାନଙ୍କର ମଧ୍ୟମ ଲବ୍‌ଧାଙ୍କକୁ ମଧ୍ୟମା କୁହାଯାଏ। ଏହା ତଥ୍ୟାବଳୀକୁ ସମାନ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରିଥାଏ।

Question ୨।
ମଧ୍ୟମାର ଦୁଇଟି ସୁଗୁଣ (Merits) ଲେଖ।
Answer:
ମଧ୍ଯମାର ଦୁଇଟି ସୁଗୁଣ ହେଲା-
(i) ମୁକ୍ତ ସୟାଗଯୁକ୍ତ ଶ୍ରେଣୀରେ ମଧମାର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କରାଯାଇପାରେ।
(ii) ମଧ୍ୟମା ରେଖାଚିତ୍ର ମାଧ୍ୟମରେ ନିର୍ଣ୍ଣୟ କରାଯାଏ।

Question ୩।
ଗରିଷ୍ଠକ (Mode) କାହାକୁ କୁହାଯାଏ ?
Answer:
କୌଣସି ବିତ ରଣରେ ସର୍ବାଧ‌ିକ ଥର ଆବିର୍ଭାବ ହେଉଥ‌ିବା ଲବ୍‌ଧାଙ୍କକୁ ଗରିଷ୍ଠକ କୁହାଯାଏ। ଅନ୍ୟ ଅର୍ଥରେ, ସର୍ବାଧ‌ିକ ବ୍ୟକ୍ତିଗତ ବାରମ୍ବାରତା ଥିବା ଲବ୍‌ଧାଙ୍କକୁ ଗରିଷ୍ଠକ କୁହାଯାଏ। ସାଧାରଣତଃ, ୩୦, ଦ୍ବାରା ଚିହ୍ନଟ କରାଯାଇଥାଏ।

Question ୪।
ଗରିଷ୍ଠକର ଦୁଇଟି ଦୁର୍ଗୁଣ (Demerits) ଲେଖ।
Answer:
ମାଧ୍ଯମାନର ଦୁଇଟି ଦୁର୍ଗୁଣ ହେଲା
(i) ମାଧ୍ଯମାନ ଚରମ ଲବ୍‌ଧାଙ୍କ ଦ୍ଵାରା ପ୍ରଭାବିତ ହୁଏ।
(ii) ମାଧ୍ଯମାନର ମୂଲ୍ୟକୁ ରେଖାଚିତ୍ର ମାଧ୍ୟମରେ ଉପସ୍ଥାପନ କରାଯାଇପାରେ ନାହିଁ।

Question ୫।
ମାଧ୍ଯମାନର ଦୁଇଟି ଦୁର୍ଗୁଣ (Demerits)ଲେଖ।
Answer:
ଗରିଷ୍ଠକର ଦୁଇଟି ଦୁର୍ଗୁଣ ହେଲା-
(i) ଏହା ଅଧୂକ ଗାଣିତିକ ବାଖ୍ୟା ସମ୍ଭବପର ନୁହେଁ, ଏବଂ
(ii) ମାଧ୍ୟମାନ ତୁଳନାରେ ଗରିଷ୍ଠକ ଚୟନ ଅସ୍ଥିରତା ଦ୍ବାରା ଅଧ‌ିକ ପ୍ରଭାବିତ ହୁଏ।

Question ୬।
ଏକ ଆଦର୍ଶ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପକର ଦୁଇଟି ଗୁଣାବଳୀ (features) ଲେଖ।
Answer:
ଗୋଟିଏ ଆଦର୍ଶ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା ମାପକର ଦୁଇଟି ଗୁଣାବଳୀ ହେଲା
(i) ଏହା ସରଳ ଓ ବୋଧଗମ୍ୟ ହେବା ଆବଶ୍ୟକ।
(ii) ଏହା ତଥ୍ୟାବଳୀର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ଆଧାରିତ।

Question ୭।
ମାଧ୍ୟମାନ (Arithmetic Mean) କାହାକୁ କୁହାଯାଏ ?
Answer:
ଗୋଟିଏ ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ମାନଙ୍କର ସମଷ୍ଟି ଓ ଲବ୍‌ଧାଙ୍କ ମାନଙ୍କର ସଂଖ୍ୟାର ଅନୁପାତକୁ ମାଧ୍ୟମାନ କୁହାଯାଏ। ଏହା ସାଧାରଣତଃ x̄ ଦ୍ଵାରା ସୂଚିତ ହୋଇଥାଏ।

Question ୮।
ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି (.). କାହାକୁ କୁହାଯାଏ ?
Answer:
ରାଶିମାଳର ଉର୍ଦ୍ଧ୍ଵ ଚତୁର୍ଥାଂଶକୁଏବଂ ନିମ୍ନ ଚତୁର୍ଥାଂଶକ ଦ୍ଵୟର ଅନ୍ତରଫଳର ଅର୍ଦ୍ଧେକକୁ ଉକ୍ତ ରାଶିମାଳାର ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି କୁହାଯାଏ। ସାଙ୍କେତିକ ଭାଷାରେ
Q.D. = \(\frac{Q_3-Q_1}{2}\)

Question ୯।
ଲରେଞ୍ଜ ବକ୍ର (Lorenz Curve) କ’ଣ ?
Answer:
ଲେଖଚିତ୍ର ମାଧ୍ୟମରେ ବିଚ୍ଛୁରଣ ପରିମାପକର ଅଧ୍ୟାୟ ଓ ଅନୁଶୀଳନକୁ ଲରେଞ୍ଜ ବକ୍ର କୁହାଯାଏ । ଆୟ ବଣ୍ଟନରେ ଅସମାନତା ଅନୁଧ୍ୟାନ କରିବା ପାଇଁ ମାକ୍‌ସ ଓ ଇରେଞ୍ଜ ସର୍ବପ୍ରଥମେ ଏହି ପଦ୍ଧତିର ବ୍ୟବହାର କରିଥିଲେ। ଏହା ଏକ ରାଶିକୃତ ଶତାଂଶ ବକ୍ରରେଖା।

Question ୧୦।
ମାନକ ବିଚ୍ୟୁତି (Standard Deviation) କାହାକୁ କୁହାଯାଏ ?
Answer:
କୌଣସି ରାଶିମାଳୀର ମାଧ୍ଯମାନ ଓ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ଅନ୍ତର ବା ବିଚ୍ୟୁତିର ବର୍ଗର ମାଧ୍ଯମାନର ବର୍ଗମୂଳକୁ ମାନ ବିଚ୍ୟୁତି କୁହାଯାଏ। ମାନବ ବିଚ୍ୟୁତିକୁ ସାଙ୍କେତିକ ଚିହ୍ନ ଓ (Sigma) ରେ ଚିହ୍ନଟ କରାଯାଏ। ସାଙ୍କେତିକ ଭାଷାରେ
\(\sigma=\sqrt{\frac{\Sigma x^2}{\mathrm{~N}}}\)

Question ୧୧।
ବିସ୍ତାର (Range) କାହାକୁ କୁହାଯାଏ ?
Answer:
ରାଶିମାଳ, ଅନ୍ତର୍ଗତ ସର୍ବବୃହତ ଓ କ୍ଷୁଦ୍ରତମ ଲବ୍‌ଧାଙ୍କ ଦ୍ଵୟର ଅନ୍ତରଫଳକୁ ବିସ୍ତାର କୁହାଯାଏ । ସାଙ୍କେତିକ ଭାଷାରେ ବିସ୍ତାର (R) = L – S କିମ୍ବା
HV – tv ଏଠାରେ,
HV = ବୃହତ୍ତମ ଲବ୍‌ଧାଙ୍କ,
LV – କ୍ଷୁଦ୍ରତମ ଲବ୍‌ଧାଙ୍କ

Question ୧୨।
ବିଚ୍ଛୁରଣର ବିଶୁଦ୍ଧ ମାପକ (Absolute) କାହାକୁ କୁହାଯାଏ ?
Answer:
ବିତରଣର ରାଶିମାଳା ଯେଉଁ ଏକକରେ ପ୍ରକାଶିତ ହୋଇଥାଏ, ବିଚ୍ଛୁରଣ ମାପକ ସେହି ଏକକରେ ପ୍ରକାଶିତ ହେଲେ ତାହାକୁ ବିଚ୍ଛୁରଣର ବିଶୁଦ୍ଧ ମାପକ କୁହାଯାଏ । ଉଦାହରଣସ୍ୱରୂପ, ଯଦି ତଥ୍ୟାବଳୀର ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକ କିଲୋଗ୍ରାମ୍ ଆକାରରେ ଦିଆଯାଇଛି, ତେବେ ଉତ୍ତର ନିଶ୍ଚୟ କଲାବେଳେ ଉତ୍ତରକୁ ସେହି ଏକକ (କିଲୋଗ୍ରାମ୍)ରେ ପ୍ରକାଶ କରାଯିବ।

Question ୧୩।
ବିଚରଣ ଗୁଣାଙ୍କ (Coefficient of variation) କାହାକୁ କୁହାଯାଏ ?
Answer:
ମାନକ ବିଚ୍ୟୁତି ଓ ମାଧ୍ଯମାନର ଶତକଡ଼ା ଅନୁପାତକୁ ବିଚରଣ ଗୁଣାଙ୍କ କୁହାଯାଏ । ସାଙ୍କେତିକ ଭାଷାରେ,

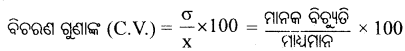
Question ୧୪।
ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ମାପକ (Relative Measures of Dispersion) କାହାକୁ କୁହାଯାଏ ?
Answer:
ବିତରଣର ରାଶିମାଳା ଯେଉଁ ଏକକରେ ପ୍ରକାଶିତ ହୋଇଥାଏ, ବିଚ୍ଛୁରଣର ମାପକ ସେହି ଏକକରେ ପ୍ରକାଶିତ ନ ହେଲେ, ତାହାକୁ ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ମାପକ କୁହାଯାଏ। ଅନ୍ୟ ଅର୍ଥରେ, ଆପେକ୍ଷିକ ମୂଲ୍ୟ, ଶତକଡ଼ା ଓ ଅନୁପାତ ଇତ୍ୟାଦିରେ ପ୍ରକାଶିତ ହେଉଥିବା ବିଜୁରଣ ମାପକକୁ ଆପେକ୍ଷିକ ମାପକ କୁହାଯାଏ। ଏହାର ମୂଲ୍ୟ ସର୍ବଦା ଏକ (i) ଠାରୁ କମ୍ ହୋଇଥାଏ।

Question ୧୫।
ବିଜୁରଣ (Dispersion) କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ବିଚ୍ଛୁରଣର ଅର୍ଥ ହେଲା ବିଭିନ୍ନତା ବା ଦୂରତା ତଥ୍ୟାବଳୀର ବିଚ୍ଛୁରଣ କହିଲେ କେନ୍ଦ୍ରୀୟ ମୂଲ୍ୟଠାରୁ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ହାରାହାରି ଦୂରତାକୁ ବୁଝାଏ। ତଥ୍ୟାବଳୀର ସଙ୍ଗତି ଅଧ‌ିକ ହେଲେ ବିଚ୍ଛୁରଣ କମ୍ ହୋଇଥାଏ।

Question ୧୬।
ଯଦି ୧୦୪ ଜଣ ଛାତ୍ରଙ୍କର ହାରାହାରି ନମ୍ବର ୮୦ ଏବଂ ୫୦ ଜଣ ଛାତ୍ରିଙ୍କର ହାରାହାରି ନମ୍ବର ୩୦ ହୁଏ, ତେବେ ୧୫୦ ଜଣ ଛାତ୍ର-ଛାତୀଙ୍କର ଯୁଗ୍ମ ମାଧ୍ଯମାନ କେତେ ହେବ?
Answer:

Question ୧୭।
100 ଜଣ ଛାତ୍ରଙ୍କର ହାରାହାରି ନମ୍ବର 60। କଂପୁଟର ଭୁଲ୍ ବସତ ଜଣେ ଛାତ୍ରର ନମ୍ବର 70 ପରିବର୍ତ୍ତେ 50 ହୋଇଛି, ତେବେ ସଠିକ୍ ହାରାହାରି ନମ୍ବର କେତେ ହେବ ?
Answer:
\(\bar{X}=\frac{\Sigma X}{N} \text { Or, } \Sigma x=\bar{X} \cdot N\)
= 100 × 60 = 6000
ସଠିକ୍ Σx = ଭୁଲ Ex = ଭୁଲ ନମ୍ବର + ସଠିକ୍ ନମ୍ବର
6000 – 50 + 70 = 5550 + 60 = 5610
∴ x̄ = \( \frac{5610}{100}\) = 56.10

IV. ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ।
[Distinguish between]

Question ୧।
ମାଧ୍ୟମାନ (Mean) ଏବଂ ମଧ୍ୟମା (Median)
Answer:
ମାଧମାନ :
(i) .ମାଧ୍ଯମାନ ଏକ ଗାଣିତିକ ହାରାହାରି।
(ii) ମାଧ୍ଯମାର ମୂଲ୍ୟକୁ ରେଖାଚିତ୍ର ମାଧ୍ୟମରେ ଉପସ୍ଥାପନ କରାଯାଇ ପାରିବ ନାହିଁ।
(iii) ମାଧ୍ଯମାନର ମୂଲ୍ୟ ବାରମ୍ବାରତା ବିତରଣର ସମସ୍ତ ଲବଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବସିତ।

ମଧ୍ୟମା
(i) ମଧ୍ୟମା ଏକ ଅବସ୍ଥାପିତ ହାରାହାରି।
(ii) ମଧ୍ୟମାର ମୂଲ୍ୟକୁ ରେଖାଚିତ୍ର ମାଧ୍ୟମରେ ଉପସ୍ଥାପନ କରାଯାଇପାରିବ।
(iii) ମଧ୍ୟମାର ମୂଲ୍ୟ ବାରମ୍ବାରତା ବିତରଣର ସମସ୍ତ ମୂଲ୍ୟ ଉପରେ ଆଧାରିତ ନୁହେଁ।

Question ୨।
ମଧ୍ୟମା (Median) ଏବଂ ଗରିଷ୍ଠକ (Mode):
Answer:
ମଧ୍ୟମା:
(i) ମଧ୍ୟମା କହିଲେ ଗୋଟିଏ ବାରମ୍ବାରତା ବିତରଣର ସେହି ମଝି ସଂଖ୍ୟାକୁ ବୁଝାଏ, ଯାହାକି ଏହାକୁ ସମାନ ଦୁଇଭାଗରେ ବିଭକ୍ତ କରିଥାଏ।
(ii) ମଧ୍ୟମା ନିର୍ଦ୍ଧାରଣର ପଦ୍ଧତି : \(L_1+\frac{L_2-L_1}{F} \times N / 2-C . F\)
(iii) ମଧ୍ୟମାର ରେଖାଙ୍କିତ ଉପସ୍ଥାପନକୁ ଓଜିଭ୍ (Ogive) କୁହାଯାଏ।

ଗରିଷ୍ଠକ :
(i) ଗରିଷ୍ଠକ କହିଲେ ଗୋଟିଏ ବାରମ୍ବାରତା ବିତରଣର ସର୍ବାଧ‌ିକ ଥର ଆବିର୍ଭାବ ହେଉଥୁବା ଲବ୍‌ଧାଙ୍କକୁ ବୁଝାଏ।
(ii) ଗରିଷ୍ଠକ ନିର୍ଦ୍ଧାରଣର ପଦ୍ଧତି : \(L_1+\frac{F_1-F_0}{2 F_1-F_0-F_2} \times i\)
(iii) ଗରିଷ୍ଠଳର ରେଖାଙ୍କିତ ଉପସ୍ଥାପନକୁ ହିଷ୍ଟାଗ୍ରାମ୍ କୁହାଯାଏ।

Question ୩।
ଚତୁର୍ଥାଂଶ ବିଚ୍ୟୁତି ଏବଂ ମାନକ ବିଚ୍ୟୁତି :
(Quartile deviation and standard deviation.)
Answer:
ଚତୁର୍ଥାଂଶ ବିଚ୍ୟୁତି :
(i) ଚତୁର୍ଥାଂଶ ବିଚ୍ୟୁତି ବିଚ୍ଛୁରଣ ମାପକର ଏକ ଅବସ୍ଥାପିତ ମାପକ।
(ii) ଚତୁର୍ଥାଂଶ ବିଚ୍ୟୁତି ନିର୍ଦ୍ଧାରଣର ପଦ୍ଧତି ହେଲା : \(\frac{N+1}{4}\) କିମ୍ବା \(\frac{N}{4}\)
(iii) ଚତୁର୍ଥାଂଶ ବିଚ୍ୟୁତିର ମୂଲ୍ୟ ବାରମ୍ବାରତା ବିତରଣର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ଆଧାରିତ ନୁହେଁ।

ମାନକ ବିଚ୍ୟୁତି :
(i) ମାନକ ବିଚ୍ୟୁତି ବିଚ୍ଛୁରଣ ମାପକର ଏକ ଗାଣିତିକ ମାପକ।
(ii) ମାନକ ବିଚ୍ୟୁତି ନିର୍ଦ୍ଧାରଣ ପଦ୍ଧତି ହେଲା
\(\sigma=\sqrt{\frac{\sum x^2}{n}}\)
(iii) ଏହା ବାରମ୍ବାରତା ବିତରଣର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ଆଧାରିତ।

Question ୪।
ମାଧବିଚ୍ୟୁତି ଓ ମାନକ ବିଚ୍ୟୁତି
(Mean deviation and stanard deviation.)
Answer:
ମାଧବିଚ୍ୟୁତି :
(i) ମାଣବିଦ୍ୟୁତିର ମୂଲ୍ୟକୁ ମଧ୍ୟମା କିମ୍ବା ମାଧମାନ ରୁ ନିର୍ଦ୍ଧାରଣ କରାଯାଏ।
(ii) ମାଧ୍ୟବିଚ୍ୟୁତି ନିର୍ଦ୍ଧାରଣର ପଦ୍ଧତି ହେଲା :
\(\text { S.D. }=\sqrt{\frac{\Sigma(\mathrm{X}-\overline{\mathrm{X}})^2}{\mathrm{n}}}\)

Question ୫।
ବିଚ୍ଛୁରଣର ସ୍ଥୂଳ ମାପକ ଓ ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ମାପକ
(Absolute measure of dispesion and relative measure of disparsion.)
ବିଚ୍ଛୁରଣର ସ୍ଥୁଳ ମାପକ :
Answer:
(i) ବାରମ୍ବାରତା ବିତରଣ ଯେଉଁ ଏକକରେ ଦିଆଯାଉଛି, ବିଚ୍ଛୁରଣର ମୂଲ୍ୟକୁ ସମାନ ଏକକରେ ପ୍ରକାଶ କରାଯାଏ।
(ii) ବିଚ୍ଛୁରଣର ସ୍ଥୁଳ ମାପକ ଗୁଡ଼ିକ ହେଲା– ବିସ୍ତାର, ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି, ମାଧବିଚ୍ୟୁତି, ମାନକ ବିଚ୍ୟୁତି ଏବଂ ପ୍ରସରଣ।

ମାପକ ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ମାପକ :
(i) ବାରମ୍ବାରତା ବିତରଣ ଯେଉଁ ଏକକରେ ଦିଆଯାଇଛି, ବିଚ୍ଛୁରଣ ଗୁଣାଙ୍କର ମୂଲ୍ୟ ସେହି ଏକକରେ ନିର୍ଦ୍ଧାରଣ କରାଯାଏ ନାହିଁ।
(ii) ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ଏକକ ଗୁଡ଼ିକ ହେଲା- ବିସ୍ତାର ଗୁଣାଙ୍କ, ମାଧ୍ୟବିଚ୍ୟୁତି ଗୁଣାତ୍ତ୍ୱିକ ଓ ମାନକ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ ଇତ୍ୟାଦି।

Question ୬।
ମାଧ୍ୟମାନ (Mean) ଏବଂ ଗରିଷ୍ଠକ (Mode):
Answer:
ମାଧ୍ୟମାନ :
(i) ମାଧ୍ଯମାନ ଏକ ଗାଣିତିକ ହାରାହାରି।
(ii) ମାଧ୍ଯମାନର ମୂଲ୍ୟ ସମସ୍ତ ଏକକ ଉପରେ ଆଧାରିତ।
(iii) ମାଧ୍ଯମାନର ମୂଲ୍ୟକୁ ରେଖା ଚିତ୍ର ସାହାଯ୍ୟରେ ଉପସ୍ଥାପନ କରାଯାଇପାରିବ ନାହିଁ।

ଗରିଷ୍ଠକ :
(i) ଗରିଷ୍ଠକ ଏକ ଅବସ୍ଥାପିତ ହାରାହାରି।
(ii) ଗରିଷ୍ଠକର ମୂଲ୍ୟ ସମସ୍ତ ଏକକ ଉପରେ ଆଧାରିତ ନୁହେଁ।
(i) ଗରିଷ୍ଠକର ମୂଲ୍ୟକୁ ରେଖାଚିତ୍ର ସାହାଯ୍ୟରେ ଉପସ୍ଥାପନ କରାଯାଇପାରିବ।

Question ୭।
ବିସ୍ତାର (Range) ଏବଂ ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି (Q.D.):
Answer:
ବିସ୍ତାର:
(i) ବିସ୍ତାର ମୂଲ୍ୟ ଗୋଟିଏ ବାରମ୍ବାରତା ବିତରଣର ଦୁଇଟି ସୀମା ଉପରେ ଆଧାରିତ।
(ii) ସାଙ୍କେତିକ ଭାଷାରେ, R = H.V. – L.V.
(iii) ବିସ୍ତାର ଗୁଣାଙ୍କର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣର ପଦ୍ଧତି ହେଲା-
E.x. – R = \(\frac{\text { H.L. }- \text { H.L. }}{\text { H.L. }+ \text { H.L }}\)

ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି :
(i) ଚତୁର୍ଥାଂଶକ ବିଦ୍ୟୁତିର ମୂଲ୍ୟ ଦୁଇଟି ଚତୁର୍ଥାଂଶକର ଅନ୍ତର ସହିତ ଦୁଇ ଭାଗ କରି ନିର୍ଣ୍ଣୟ କରାଯାଏ।
(ii) ସାଙ୍କେତିକ ଭାଷାରେ, Q.D. = \(\frac{Q_3-Q_1}{2}\)
(iii) ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣରୁ ପଦ୍ଧତି ହେଲା ,
Q.D. = \(\frac{Q_3-Q_1}{Q_3+Q_1}\)

Question ୮।
ବିସ୍ତାର (Range) ଏବଂ ମାନକ ବିଚ୍ୟୁତି (S.D):
Answer:
ବିସ୍ତାର:
(i) ଏହା ଏକ ଅବସ୍ଥାପିତ ବିଜୁରଣର ମାପକ।
(ii) ବିସ୍ତାର ଗୋଟିଏ ବାରମ୍ବାରତା ବିତରଣର ଦୁଇଟି ସୀମା ଉପରେ ପର୍ଯ୍ୟବେସିତ।
(iii) ଏହା ବିଚ୍ଛୁରଣର ଏକ ସରଳମାପକ।

ମାନକ ବିଚ୍ୟୁତି :
(i) ଏହା ଏକ ଗାଣିତିକ ବିଚ୍ଛୁରଣର ମାପକ।
(ii) ଏହା ବାରମ୍ବାରତା ବିତରଣର ସମସ୍ତ ଏକକ ଉପରେ ପର୍ଯ୍ୟବସିତ
(iii) ଏହା ବିଚ୍ଛୁରଣର ଏକ ସରଳ ମାପକ ନୁହେଁ।

V. ଦୀର୍ଘଧର୍ମୀ ପ୍ରଶ୍ନୋତ୍ତର।
[Long Answer type Questions]

Question ୧।
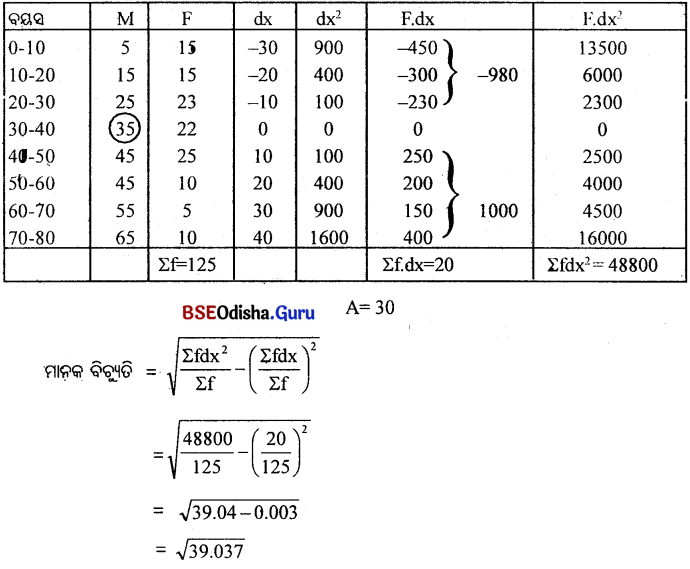
ମାନକ ବିଚ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର।
(Determine the value of Standard of deviation.)

ବୟସ (X)	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80
ଛାତ୍ରଙ୍କର ସଂଖ୍ୟା (F)	15	15	23	22	25	10	5	10

Answer:
ମାନକ ବିଚ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ-

Question ୨।
ମାଧ୍ଯମାନର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର। (Determine the value of Mean.)
X: 10, 12, 14, 16, 18
ମାଧ୍ୟମାନର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ ( ପ୍ରତ୍ୟକ୍ଷ ପଦ୍ଧତି)

x	(dx)  (x – A)
10	-4
12	-2
14	0
16	2
18	4
X – 70	Σdx = 0

x̄ (ମାଧ୍ୟମାନ) = \(\frac{\sum X}{n}=\frac{70}{5}\) = 14
x̄ = A + \(\frac{\Sigma \mathrm{dx}}{\mathrm{~N}}\)
= 14 + \(\frac{0}{5}\) =  14 + 0 = 14
∴ ମାଧ୍ଯମାନର ମୂଲ୍ୟ 14

Question ୩।
ମାଧ୍ଯମାନର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର। (Determine the value of mean.)

Marks (X)	10	20	30	40	50	60	70
No. of Students (F)	5	8	10	20	15	7	5

Answer:
ମାଧମାନର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ (ସଂକ୍ଷିପ୍ତ ପଦ୍ଧତି)

Question ୪।
ମାଧ୍ୟମାନର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର।
(Determine the value of Mean.)

ନମ୍ବର (X)	0-10	10-20	20-30	30-40	40-50	50-60
ଛାତ୍ରଙ୍କର ସଂଖ୍ୟା (F)	4	6	10	8	12	5

Answer:

ନମ୍ବର (X)	ଛାତ୍ରଙ୍କର ସଂଖ୍ୟା (F)	ନମ୍ବର	ଛାତ୍ରଙ୍କର ସଂଖ୍ୟା	M	F.M
0-10	4	0-10	4	5	20
10-20	6	10-20	6	15	90
20-30	10	20-30	10	25	250
30-40	8	30-40	8	35	280
40-50	12	40-50	12	45	540
50-60	5	50-60	5	55	275
			Σf = 45		Σfm = 1455

x̄ = \(\frac{\Sigma \mathrm{fm}}{\Sigma \mathrm{f}}=\frac{1455}{45}\) = 32.35
∴ ମାଧ୍ୟମାନର ମୂଲ୍ୟ 32.33

ମାଧ୍ଯମାନର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ ( ସଂକ୍ଷିପ୍ତ ପଦ୍ଧତି)

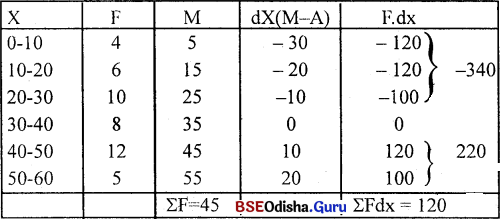
ବିରବିଚ୍ଛିନ୍ନ ବାରମ୍ବାରତା ବିତରଣ (ସଂକ୍ଷିପ୍ତ ପଦ୍ଧତି)
x̄ = A + \(\frac{\Sigma \mathrm{Fdx}}{\Sigma \mathrm{f}}\) = 35 – \(\frac{120}{45}\)
5 = 35 – 2.66
= 32.34
∴ ମାଧ୍ୟମାନର ମୂଲ୍ୟ 32.34.

Question ୫।
ମଧ୍ୟମାର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର (Determine the value of Median.)

ନମ୍ବର (X)	0-10	10-20	20-30	30-40	40-50
ଛାତ୍ରଙ୍କର ସଂଖ୍ୟା (F)	4	8	11	9	10

ମଧ୍ୟମାର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ

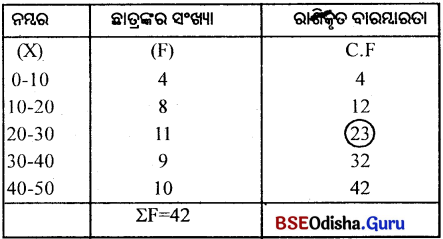
ମଧ୍ୟମା = \(\frac{N}{2}\) ତମ ସଂଖ୍ୟା
= \(\frac{42}{2}\) = 21 ତମ ସଂଖ୍ୟା
21 ତମ ସଂଖ୍ୟା C.F. ର 23 ରେ ରହିଛି।
23 ବିରୁଦ୍ଧରେ ଶ୍ରେଣୀ ହେଲା 20-30।
ତେଣୁ 20-30 ମଧ୍ଯମାର ଶ୍ରେଣୀ। ମଧ୍ୟମାର ଶ୍ରେଣୀରୁ ମଧ୍ୟମାର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କରାଯାଇଅଛି।

ମଧ୍ୟମା (Md) = \(L_1+\frac{L_2+L_1}{F} \times N / 2-C . F\)
\(20+\frac{30-20}{11} \times 21-12\)
20 + \(\frac{10}{11}\) × 9
= 20 + \(\frac{90}{11}\)
= 20 + 8.18 = 28.18
∴ ମାଧ୍ୟମାନର ମୂଲ୍ୟ 28.18

Question ୬।
ଚତୁର୍ଥାଶଂକ ବିଦ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର।
(Determine the value of Quartile deviation.)

କୋଠରୀର ସଂଖ୍ୟା (X)	ରହୁଥ‌ିବା ଲୋକମାନଙ୍କର ସଂଖ୍ୟା (F)
10	5
12	8
14	11
16	10
18	9
20	4

ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ

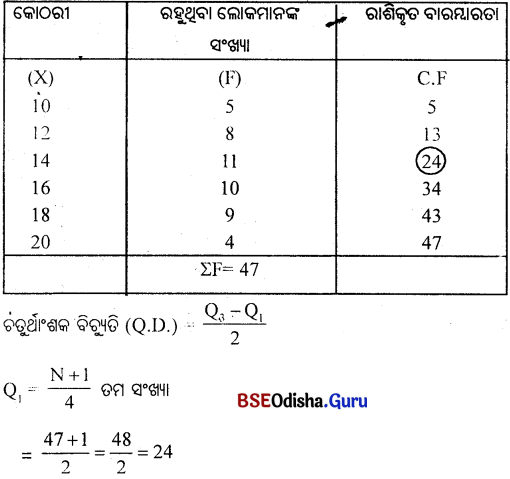
ରାଶିକୃତ ବାରମ୍ବାରତାର 24 ରେ Q₁ ର ମୂଲ୍ୟ ରହିଛି। 24 ବିରୁଦ୍ଧରେ ସଂଖ୍ୟା 14 Q₁ ର ମୂଲ୍ୟ 14।
24 ବିରୁଦ୍ଧରେ ପରିବର୍ତ୍ତନରେ ହେଲା 1 4
Q₁ ର ମୂଲ୍ୟ।

Q₃ = \(\frac{3(n+1)}{4}=\frac{3(48)}{4}=\frac{144}{4}\) = 36
36 ତମ ସଂଖ୍ୟା c.ର 43 ରେ ରହିଛି 43 ବିରୁଦ୍ଧରେ ମୂଲ୍ୟ 18
Q₃  ର ମୂଲ୍ୟ = 18
Q = \(\frac{Q_3-Q_1}{2}\)
\(\frac{4}{2}\) = 2
∴ Q. Dର ମୂଲ୍ୟ 2।

Question ୭।
ଗରିଷ୍ଠକର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର। (Determine the value of Mode.)

Marks (X)	0-10	10-20	20-30	30-40	40-50
No of Students (F)	5	11	15	10	7

ଗରିଷ୍ଠକର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ

Marks (X)	No. of Students (F)
0-10	5
10-20	11
20-30	15
20-30	10
30-40	7
30-40	10
40-50	7

ଗରିଷ୍ଠକର ଶ୍ରେଣୀ 20-30 ଏହାର କାରଣ ହେଲା ସର୍ବୋଚ୍ଚ ବ୍ୟକ୍ତିଗତ ବାରମ୍ବାରତାର ମୂଲ୍ୟ 15। ଏହା 20- 30 ଶ୍ରେଣୀରେ ରହିଛି।

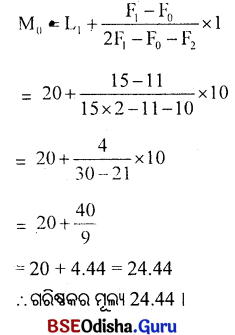
Question ୮।
ମାଧ୍ୟ ବିଚ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର। (Determine the value of mean deviation.)

Marks (X)	No. of Students(F)
0-10	4
10-20	6
20-30	10
30-40	7
40-50	3
50-60	5

Answer:
ମାଧ୍ୟ ବିଦ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର

X	F	M	F.M	X-x̄	F.X
0-10	4	5	20	+33	132
10-20	6	15	90	23	138
20-30	10	25	250	13	130
30-40	7	35	245	3	21
40-50	3	45	135	7	21
50-60	5	55	275	17	85
	ΣF = 35		ΣFm = 1015		ΣFx = 527

x̄ = \(\frac{\Sigma \mathrm{Fm}}{\Sigma \mathrm{f}}=\frac{1015}{35}\) = 38
M.D = \(\frac{\Sigma \mathrm{f}|\mathrm{X}-\overline{\mathrm{X}}|}{\Sigma \mathrm{f}}\) = \(\frac{527}{35}\) = 15.05
∴ ମାଧ୍ୟ ବିଦ୍ୟୁତିର ମୂଲ୍ୟ 15.05

Question ୯।
ଗରିଷ୍ଠକର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ। (Determine the value of Mode.)
କର୍ମଚାରୀମାନଙ୍କର

ଦରମା (X)	କର୍ମଚାରୀମାନଙ୍କର ସଂଖ୍ୟା (F)
1000	10
2000	20
3000	15
4000	30
5000	31
6000	5
7000	11

Answer:
Grouping Table

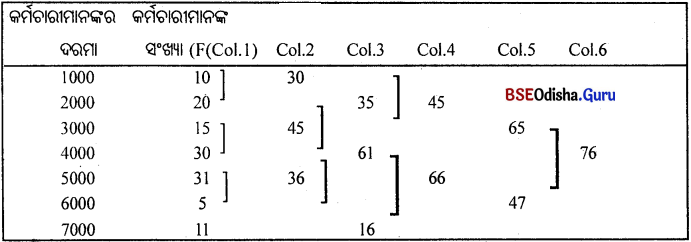
Analysis Table

Col.No.	1000	2000	3000	4000	5000	6000	7000
1					1
2			1	1
3				1	1
4				1	1	1
5	1	1	1	1
6		1	1	1	1
Total	0	1	3	5	4	2	0

ଉପରୋକ୍ତ ବିଶ୍ଳେଷଣ ସାରଣୀରୁ ଏହା ସ୍ପଷ୍ଟ ହୁଏ ଯେ ଟ.5000 ଦରମା ସର୍ବାଧ‌ିକ 5 ଥର ରହିଛି। ତେଣୁ ଗରିଷ୍ଠକର ମୂଲ୍ୟ ଟ.5000।

Question ୧୦।
ଗରିଷ୍ଠକର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ। (Determine the values of Mode.)

X:	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80
F:	5	11	15	21	22	17	10	6

Answer:

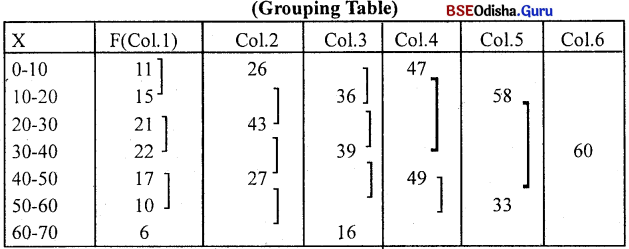
Analysis Table

Col.No.	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80
1				1
2			1	1
3				1	1
4				1	1	1
5		1	1	1
6				1	1
Total	0	1	3	5	4	2	0	0

30 – 40 ଶ୍ରେଣୀ ସର୍ବାଧିକ ସ୍ତର ରହିଛି। ଏହାକୁ ଗରିଷ୍ଠକ ଶ୍ରେଣୀ କୁହାଯାଏ। ଏହି ଶ୍ରେଣୀର ଗରିଷ୍ଠକର ମୂଲ୍ୟ ନିଦ୍ଧାରଣ କରାଯିବ।

Question ୧୧।
ଯଦି x̄ = 40, x̄₂ = 50, N₂ = 100, 6₁ = 3, 6₂ = 4
ଯୁଗ୍ମମାନକ ବିଚ୍ୟୁତର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର।
Answer:
ଯୁଗ୍ମମାଧ୍ଯମାନ

Question ୧୨।
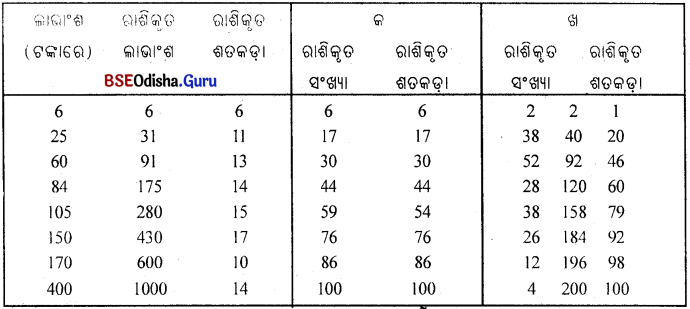
ଲୋରେଞ୍ଚ ବକ୍ର ସାରଣୀ ଗଠନ କର। (Construct a Lorenz Curve Table:)

ଲାଭାଂଶ (ଟଙ୍କାରେ)	କଂପାନୀର ସଂଖ୍ୟା ଅଞ୍ଚଳ (କ)	ଅଞ୍ଚଳ
6	6	2
25	11	38
60	13	52
84	14	28
105	15	38
150	17	26
170	10	12
400	14	2

Answer:
ଲୋରେଞ୍ଚ ବକ୍ର ସାରଣୀ (Lorenz Curve Schedule.)

Question ୧୩।
ଯଦି, ୧୪୦ ଜଣ ଛାତ୍ରଙ୍କର ହାରାହାରି ନମ୍ବର ୪୦ ଏବଂ ମାନକ ବିଦ୍ୟୁତିର ମୂଲ୍ୟ ୫। କଂପ୍ୟୁଟର ଭୁଲବସତଃ ଜଣେ ଛାତ୍ରଙ୍କର ନମ୍ବର ୪୦ ପରିବର୍ତ୍ତେ୫୦ ହୋଇଛି, ତେବେ ସଠିକ୍ ହାରାହାରି ନମ୍ବର ଏବଂ ମାନକ ବିଚ୍ୟୁତି କେତେ ହେବ ?
(If average marks of 140 students is 40 and standard deviation is 5. By the mistake of a computer the marks of a student is wrongly taken as 50 instead of 40), then calculate the correct average marks.)
Answer:
x̄ = \(\frac{\Sigma x}{N}\)
ΣΧ = N.x̄
ଏଠାରେ, N = 100, x̄ = 40
ΣΧ = 100 × 40 = 4000
ସଠିକ୍ Σx = ଭୁଲ୍ Σx – ଭୁଲ୍ ନମ୍ବର + ସଠିକ୍ ନମ୍ବର
= 4000 – 50 + 40
x̄ = \(\frac{\sum X}{N}\)
= 3950 + 40 = 3990
= \(\frac{3990}{100}\) = 39.90
\(\sigma=\sqrt{\frac{\sum x^2}{n}-(\bar{x})^2}\)
\((6)^2=\frac{\sum x^2}{n}-(\bar{x})^2\)
\((5)^2=\frac{\sum x^2}{100}-(40)^2\)
25 = \(\frac{\Sigma x^2-1600 \times 100}{100}\)
25 × 100 = Σx² – 160000
2500 = Σx² – 160000
∴ Σx² = 162500

ସଠିକ୍ ପx ଭୁଲ୍ ପx – (ଭୁଲ୍ ନମ୍ବର) + (ସଠିକ୍ ନମ୍ବର)
162500 – (50)² + (40)
162500 – 2500 + 1600
= 160000 + 1600
= 161600

∴ ସଠିକ୍ ମାଧ୍ଯମାନ 39.୨ ଏବଂ ସଠିକ୍ ମାନକ ବିଚ୍ୟୁତି 4.75 1.

Question ୧୧।
ବିଚ୍ଛୁରଣର ପରିମାପ ଆଲେଚାନା କର। (Explain measures of dispersion.)
Answer:
ଏହା ନିଶ୍ଚିତ ଯେ ବିତରଣର କେନ୍ଦ୍ରୀୟ ଅଂଶରେ ପର୍ଯ୍ୟବେକ୍ଷଣର ଘନୀଭୂତ ସଂପର୍କରେ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତାର ପରିମାପ ବା ହାରାହାରି ସମ୍ୟକ୍ ଧାରଣା ପ୍ରଦାନ କରିଥାଏ। ବଣ୍ଟନମାଳାକୁ ସଂକ୍ଷିପ୍ତ କରିବା ପାଇଁ କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତିର ପରିମାପର ଭୂମିକା ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ । କିନ୍ତୁ ତଥ୍ୟାବଳୀର ବିସ୍ତାର ଏବଂ ଅନ୍ୟାନ୍ୟ କୌଣସି ବିଷୟରେ ଏହା ଆଲୋକପାତ କରିପାରେ ନାହିଁ। ଅର୍ଥାତ୍ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତାର ପରିମାପ ଚତୁଃପାର୍ଶ୍ବରେ ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକ କିଭଳି ବିଚ୍ଛୁରିତ ହୋଇଥାନ୍ତି ସେ ସଂପର୍କରେ ସବିଶେଷ ବିବରଣୀ ପ୍ରଦାନ କରି ନ ଥାଏ। ଏହା କେବଳ ସଂପୂର୍ଣ୍ଣ ତଥ୍ୟାବଳୀକୁ ଗୋଟିଏ ମାତ୍ର ଲବ୍‌ଧାଙ୍କ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରୁଥିବାରୁ ସମୁଦାୟ ମାଳାର ସଠିକ୍ ବୃତ୍ତାନ୍ତ ପାଇବା ସମ୍ଭବ ହୋଇ ନ ଥାଏ । ସେଥୁ ନିମିତ୍ତ ଯେ କୌଣସି ବଣ୍ଟନମାଳା ବିଷୟରେ ସଂପୂର୍ଣ୍ଣ ତଥ୍ୟ ପାଇବା ପାଇଁ ବିଜୁରଣ ପରିମାପ (Measures of dispersion) ଅତ୍ୟନ୍ତ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ମନେହୁଏ।

ବିଚ୍ଛୁରଣର ଅର୍ଥ ଓ ସଂଜ୍ଞା (Meaning and Definitions of Dispersion):
କୌଣସି ତଥ୍ୟାବଳୀରେ ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକ କେନ୍ଦ୍ରୀୟ ମାପକର ଉଭୟ ପାର୍ଶ୍ଵରେ କିପରି ଭାବେ ବିଚ୍ଛୁରିତ ହୋଇ ରହିଛନ୍ତି ତାହାକୁ ବିଚ୍ଛୁରଣ କୁହାଯାଏ। ବିଜୁରଣ ଯେତେ ବେଶୀ ତଥ୍ୟାବଳୀର ସଂପରି ସେତେ କମ୍ ଓ ବିଚ୍ଛୁରଣ ଯେତେ କମ୍ ତଥ୍ୟାବଳୀର ସଂପତି ସେତେ ବେଶୀ ବୋଲି ଗ୍ରହଣ କରାଯାଇଥାଏ। ବିଜୁରଣ ଦ୍ଵାରା ତଥ୍ୟାବଳୀର ହାରାହାରି ମୂଲ୍ୟ ଓ ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକ ମଧ୍ୟରେ ଥ‌ିବା ଦୂରତା ପ୍ରଦର୍ଶିତ ହୋଇଥାଏ। ବିଜୁରଣ ମାପକୁ କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତି ପରିମାପର ଅନୁପୂରକ ଓ ସହଯୋଗୀ ରୂପେ ଗ୍ରହଣ କରାଯାଇଥାଏ। କେନ୍ଦ୍ରୀୟ ପ୍ରକୃତିର ପରିମାପ, ଯଥା : ମଧ୍ଯମାନ, ମଧ୍ୟମା ଓ ଗରିଷ୍ଠକମାଳାର ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ବାସ୍ତବ ମୂଲ୍ୟ ଥିବାରୁ ଏହାକୁ ପ୍ରଥମ ଶ୍ରେଣୀର ହାରାହାରି ( Averages of the first Order) ବୋଲି କୁହାଯାଇଥାଏ। ବିଚ୍ଛୁରଣର ମାପ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତାର ପରିମାପ ଓ ତଥ୍ୟାବଳୀର ପ୍ରତ୍ୟେକ ଲବ୍‌ଧାଙ୍କ ମଧ୍ୟରେ ଥୁବା ଦୂରତାର ହାରାହାରି ମୂଲ୍ୟ ହୋଇଥିବାରୁ ଏହାକୁ ଦ୍ଵିତୀୟକ ଶ୍ରେଣୀର ହାରାହାରି ( Averages of the second order) ବୋଲି କୁହାଯାଏ।

ପରିସଂଖ୍ୟାନବିତ୍ରମାନେ ବିଚ୍ଛୁରଣର ବିଭିନ୍ନ ସଂଜ୍ଞା ପ୍ରଦାନ କରିଛନ୍ତି । କେତେକେ ପ୍ରମୁଖ ସଂଜ୍ଞାଗୁଡ଼ିକୁ ନିମ୍ନରେ ପ୍ରକାଶ କରାଯାଇଛି। ବାଉଲେଙ୍କ ମତରେ “ଲବ୍‌ଧାଙ୍କ (Items) ର ପରିବର୍ତ୍ତିତ ପରିମାପକୁ ବିଚ୍ଛୁରଣ ବା ବିକ୍ଷେପଣ କୁହାଯାଏ ।” Accordig to Bawley “Dispersion is the measure of the variation of the item.” ବୁକ୍ ଏବଂ ଡିକ୍‌ଙ୍କ ମତରେ, “କେନ୍ଦ୍ରୀୟ ମୂଲ୍ୟର ପରିବର୍ତ୍ତିତ କାରକ (variable) ର ଭିନ୍ନତାର ହାରକୁ ବିଚ୍ଛୁରଣ କୁହାଯାଏ । ? According to Brooks and Dick “Dispersion or spread is the degree of variation of the vairable about a central value.”

ସିଜେଲେଙ୍କ ମତରେ, “ଯେଉଁ ହାରରେ ଗାଣିତିକ ତଥ୍ୟ ଏକ ହାରାହାରି ମୂଲ୍ୟ ମଧ୍ଯରେ ବିଚ୍ଛୁରିତ ହୁଏ, ତାହାକୁ ତଥ୍ୟର ବିଭିନ୍ନତା ବା ବିଚ୍ଛୁରଣ କୁହାଯାଏ ।” According to Spiegel “The degree to which numerical data tend to spread about on average value is called as the variation or dispersion of data.”

ବିଚ୍ଛୁରଣ ମାପ (Measures of Dispersion):
ବିଚ୍ଛୁରଣ ମାପଗୁଡ଼ିକୁ ମୁଖ୍ୟତଃ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇପାରେ। ଯଥା : (୧) ବିଶୁଦ୍ଧ ପରିମାପ ( Absolute teasures), (୨) ଆପେକ୍ଷିକ ପରିମାପ (Relative measures)।

(୧) ବିଶୁଦ୍ଧ ପରିମାପ (Absolute measures):
ବିଚ୍ଛୁରଣର ପରିମାପ ଯାହାକୁ ବିତରଣମାଳାର ମୌଳିକ ଏକକରେ ପ୍ରକାଶ କରାଯାଏ, ତାହାକୁ ବିଶୁଦ୍ଧ ପରିମାପ ବୋଲି କୁହାଯାଏ। ଏହି ପରିମାପ ଲବ୍‌ଧାମାନଙ୍କର କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତିର ପରିମାପରୁ ବିଚ୍ୟୁତିକୁ ହିସାବକୁ ନେଇଥାଏ। ସେଥୁପାଇଁ ରାଶିମାଳାର ମୌଳିକ ଏକକରେ ସେଗୁଡ଼ିକ ପ୍ରକାଶିତ ହୋଇଥାନ୍ତି। ଉଦାହରଣ ସ୍ଵରୂପ, ଛାତ୍ରମାନଙ୍କର ଉଚ୍ଚତା ଓ ଓଜନର ବିଚ୍ଛୁରଣର ବିଶୁଦ୍ଧ ପରିମାପ ଯଥାକ୍ରମେ ଇଞ୍ଚ ଫୁଟ ଓ କିଲୋଗ୍ରାମରେ ପ୍ରକାଶିତ ହୁଏ। ମାତ୍ର ଇଞ୍ଚା ଫୁଟ ଓ କିଲୋଗ୍ରାମ୍ ଉଭୟ ଦୁଇ ଭିନ୍ନ ଭିନ୍ନ ଏକକ ଅଟନ୍ତି। ଏହି କ୍ଷେତ୍ରରେ ଏକକର ବିଭିନ୍ନତାକୁ ବିଶୁଦ୍ଧ ପଦ୍ଧତିରେ ମପାଯାଇପାରିବ ନାହିଁ। ତାହା କେବଳ ଆପେକ୍ଷିକ ପରିମାଣ ଦ୍ବାରା ମପାଯାଇପାରିବ। ବିସ୍ତାର (Range), ଆନ୍ତଃଚତୁର୍ଥାଂଶ ବିସ୍ତାର ବା ଚତୁର୍ଥାଂଶକ (Standard deviation) ବିଶୁଦ୍ଧ ପରିମାପର ଅନ୍ତର୍ଭୁକ୍ତ।

(୨) ଆପେକ୍ଷିକ ପରିମାପ (Relative measures):
ବିଚ୍ଛୁରଣର ଆପେକ୍ଷିକ ପରିମାପକୁ ବିଜୁରଣର ଗୁଣାଙ୍କ କୁହାଯାଏ । କିଛି ଆପେକ୍ଷିକ ମୂଲ୍ୟ ବା ଶତକଡ଼ା ମାଧ୍ୟମରେ ତଥ୍ୟାବଳୀର ପରିବର୍ତ୍ତନୀୟତା ପ୍ରକାଶକୁ ବିଜୁରଣର ଆପେକ୍ଷିକ ପରିମାପ ବୋଲି କୁହାଯାଏ। ସେଥ‌ିପାଇଁ ଏହି ପରିମାପକୁ ସ୍ଵତନ୍ତ୍ର ଏକକର ବାସ୍ଵ ସଂଖ୍ୟା ବୋଲି କୁହାଯାଏ । ଏହା ସର୍ବାଧ‌ିକ ମୂଲ୍ୟ ଓ ସର୍ବନିମ୍ନ ମୂଲ୍ୟର ଅନୁପାତ ଓ ସେମାନଙ୍କର ସମ୍ରାଣକୁ ବୁଝାଏ । ବିସ୍ତାର ଗୁଣାଙ୍କ (Coefficient of range) ଚତୁର୍ଥାଂଶକ ବିଦ୍ୟୁତିର ଗୁଣାଙ୍କ (Coefficient of Quartile Deviation) ମାଧ୍ୟ ବିଦ୍ୟୁତିର ଗୁଣାଙ୍କ (Coeflicient of mean deviation) ମାନଙ୍କ ବିଚ୍ୟୁତିର ଗୁଣାଙ୍କ (Coellicient of standard deviation)। ବିଚରଣ ଗୁଣାଙ୍କର (Coefficient of variation) ଏବଂ ଲରେଞ୍ଜ ବକ୍ସ (Lorenz Curve) ଅନ୍ତର୍ଭୁକ୍ତ।

Question ୧୨।
ବିସ୍ତାର (Range) କ’ଣ ? ବିସ୍ତାରର ସୁଗୁଣ ଓ ଦୁର୍ଗୁଣଗୁଡ଼ିକ ଆଲୋଚନା କର।
(What is Range ? Explain its merits and demerits.)
Answer:
ବିଜୁରଣର ପରିମାପକମାନଙ୍କ ବିସ୍ତାର ସବୁଠାରୁ ସହଜ । ଦୁଇଟି ଚରମ ଲବ୍‌ଧାଙ୍କ ମଧ୍ୟରେ ଥିବା ତାରତମ୍ୟକୁ ବିସ୍ତାର କୁହାଯାଏ । ଅନ୍ୟ ଅର୍ଥରେ ପ୍ରକାଶ କଲେ ବିସ୍ତାର ହେଉଛି ବିଚରଣମାଳାର ସର୍ବବୃହତ୍ ଓ ସର୍ବକନିଷ୍ଠ ଲବ୍‌ଧାଙ୍କ ଦ୍ବୟର ଅନ୍ତରଫଳ।

ବିସ୍ତାରର ସୁଗୁଣ (Merits of Range):
(୧) ବିସ୍ତାରର ନିର୍ଣ୍ଣୟ ପଦ୍ଧତି ଅତ୍ୟନ୍ତ ସରଳ।
(୨) ଏହି ପଦ୍ଧତି ସହଜ, ବୋଧଗମ୍ୟ ଏବଂ ଏହାର ନିର୍ଣ୍ଣୟ ସ୍ଵଳ୍ପ ସମୟସାପେକ୍ଷ।
(୩) ଗୋଟିଏ ବଣ୍ଟନର ବିସ୍ତାର ସଂପର୍କର ଏହା ତୁରନ୍ତ ଫଳାଫଳ ପ୍ରଦାନ କରିଥାଏ।
(୪) ସଂପୂର୍ଣ୍ଣ ସଠିକତା ନ ଥିଲେ ମଧ୍ୟ ତୁରନ୍ତ ଫଳାଫଳ ଜାଣିବା ପାଇଁ ଏହା ବିଶେଷ ଉପଯୋଗୀ ହୋଇଥାଏ।

ବିସ୍ତାରର ଦୁର୍ଗଣ (Merits of Range):
(୧) ଏହାର ଗଣନା ତଥ୍ୟାବଳୀର ପ୍ରତ୍ୟେକ ଲବ୍‌ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବେସିତ ହୋଇ ନ ଥିବାରୁ ଏହା ଏକ ନିର୍ଭରଯୋଗ୍ୟ ପରିମାପ ନୁହେଁ।
(୨) କେବଳ ମାତ୍ର ଦୁଇଟି ଲବ୍‌ଧାଙ୍କ ଦ୍ଵାରା ନିର୍ଦ୍ଧାରିତ ହେଉଥିବାରୁ ଏହା ଅନ୍ୟାନ୍ୟ ଲବ୍‌ଧାଙ୍କର ବିଚ୍ଛୁରଣ ମାପ କରିବାକୁ ସକ୍ଷମ ନୁହେଁ।
(୩) ମୁକ୍ତ ସଂଭାଗଯୁକ୍ତ ବାରମ୍ବାରତା ବିତରଣରେ ଏହାର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କରିବା ସମ୍ଭବ ହୋଇ ନ ଥାଏ।

Question ୧୩ ।
ଆନ୍ତଃଚତୁର୍ଥାଂଶକ ବିସ୍ତାର ବା ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ଆଲୋଚନା କର।
(Explain Inter Quartile Range or Quartile Deviation.)
Answer:
ବିଚ୍ଛୁରଣର ଏହା ଅନ୍ୟ ଏକ ପରିମାପକ । ଏହା ଊର୍ଦ୍ଧ୍ବ ଚତୁର୍ଥାଂଶକ(Q),) ଓ ଅତଃଚତୁର୍ଥାଂଶକ (Q,) ଉପରେ ପର୍ଯ୍ୟବେସିତ ଅଟେ। ଊର୍ଦ୍ଧ୍ବ ଓ ଅଧଃ ଚତୁର୍ଥାଂଶକର ଅନ୍ତରଫଳର ଅର୍ଦ୍ଧେକକୁ ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ବା ଆନ୍ତଃଚତୁର୍ଥାଂଶକ ବିସ୍ତାର ବୋଲି କୁହାଯାଏ।

ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତିର ସୁଗୁଣ (Merits of Quartile Deviation):
(୧) ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ବୁଝିବାକୁ ଅତି ସହଜ ଏବଂ ଏହାର ନିର୍ଣ୍ଣୟ ପ୍ରଣାଳୀ ମଧ୍ୟ ସରଳ।
(୨) ଏହା ଚରମ ଲବ୍‌ଧାଙ୍କ ଦ୍ବାରା ପ୍ରଭାବିତ ହୋଇ ନ ଥାଏ।
(୩) ଏହା ଅବାଧ ସଂଭାଗ ବିସ୍ତାର ସହିତ ମଧ୍ୟ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ।
(୪) ଅପ୍ରତିସମ ବଣ୍ଟନ କ୍ଷେତ୍ରରେ ଏହା ମଧ୍ୟ ଉପଯୋଗୀ।

ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତିର ଦୁର୍ଗୁଣ (Demerits of Quartile Deviation):
(୧) ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ବଣ୍ଟନର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବେସିତ ହୋଇ ନ ଥିବାରୁ ଏହା ବିଚ୍ଛୁରଣର ସଠିକ୍ ପ୍ରତିନିଧ‌ିତ୍ଵ କରିବାରେ ଅସଫଳ ହୋଇଥାଏ।
(୨) ଏହା ପ୍ରଥମ ଓ ଶେଷ ୨୫ ପ୍ରତିଶତ ଲେଖାଏଁ ଇବ୍‌ଧାଙ୍କ ମାନଙ୍କୁ ଗଣନା ପରିସର ମଧ୍ୟକୁ ନେଇ ନ ଥ‌ିବାରୁ ଏହାର ପରିସର ସଂକୁଚିତ ହୋଇଥାଏ।
(୩) ନମୁନାର ପରିବର୍ତ୍ତନ ସହ ଏହାର ମୂଲ୍ୟ ପରିବର୍ତ୍ତନ ହେଉଥିବାରୁ ଏହାକୁ ଏକ ସ୍ଥିର ମାପାଙ୍କ ରୂପେ ଗ୍ରହଣ କରାଯାଏ ନାହିଁ।

ମାଧ୍ୟ ବିଚ୍ୟୁତି (Mean Deviation):
ଗୋଟିଏ ବାରମ୍ବାରତା ବିତରଣ ସାରଣୀରେ ମାଧ୍ୟମାନ ବା ମଧ୍ୟମା ଓ ଇଛାଙ୍କ ମାନଙ୍କର ପରିମାଣର ମାଧ୍ୟମାନକୁ ମାଧ୍ୟ ବିଚ୍ୟୁତି କୁହାଯାଏ। ଏହାକୁ ମଧ୍ୟ ହାରାହାରି ବିଚ୍ୟୁତି ବା ନିରଙ୍କୁଶ ବା ବିଶୁଧ ବିଚ୍ୟୁତି କୁହାଯାଏ।

ମାଧ୍ୟ ବିଦ୍ୟୁତିର ସୁଗୁଣ (Merits of Mean Deviation):
(୧) ମଧ୍ୟ ବିଚ୍ୟୁତି ନିର୍ଦ୍ଧାରଣ କଲାବେଳେ ଧନାତ୍ମକ ଓ ଋଣାତ୍ମକ ଚିହ୍ନକୁ ବିଚାରକୁ ନିଆଯାଏ ନାହିଁ। ଯାହା ଫଳରେ ଏହା ଗାଣିତିକ ମତେ ଅତ୍ୟନ୍ତ ଅପ୍ରାସଙ୍ଗିକ ଓ ତ୍ରୁଟିପୂର୍ଣ୍ଣ ଅଟେ।
(୨) ମାଧ୍ୟ ବିଦ୍ୟୁତିର ନିଜସ୍ଵ ଦୁର୍ବଳତା ଯୋଗୁଁ ବୀଜଗାଣିତିକ ବ୍ୟାଖ୍ୟାନ ପାଇଁ ଅନୁପଯୁକ୍ତ ହୋଇଥାଏ।
(୩) ମାଧ୍ୟ ବିଚ୍ୟୁତି ବିଚ୍ଛୁରଣର ସଠିକ୍ ପରିମାପକ ନୁହେଁ।
(୪) ମାଧ୍ୟ ବିଦ୍ୟୁତିର ବ୍ୟବହାର କ୍ଵଚିତ୍ ଦେଖାଯାଇଥାଏ।

Question ୧୪।
ମାନକ ବିଚ୍ୟୁତି ଆଲୋଚନା କର !
(Explain Standard Deviation.)
Answer:
ଗୋଟିଏ ବିଚରଣରେ ମାଧମାନ ଓ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ଅନ୍ତରର ବର୍ଗର ମାଧ୍ଯମାନର ଧନାତ୍ମକ ବର୍ଗମୂଳକୁ ମାନକ ବିଚ୍ୟୁତି କୁହାଯାଏ। ଏହାକୁ ବର୍ଗମୂଳ ମାଧ୍ୟମାନ ବର୍ଗ ବିଚ୍ୟୁତି କିମ୍ବା ମାଧ୍ୟମାନ ଅଶୁଦ୍ଧି (Mean crror) ବୋଲି କୁହାଯାଏ। ୧୮୯୩ ମସିହାରେ ପ୍ରଫେସର କାର୍ଲିପିଅରସନ ଏହି ତତ୍ତ୍ଵକୁ ପ୍ରତିପାଦନ କରିଥିଲେ। ବିଜୁରଣ ପରିମାପମାନଙ୍କ ମଧ୍ୟରେ ମାନକ ବିଚ୍ୟୁତି ସବୁଠାରୁ ଅଧିକ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଅଟେ । ମାନକ ବିଚ୍ୟୁତିକୁ ଗ୍ରୀକ ଶବ୍ଦ ସିଗମ (ଓ) ଦ୍ଵାରା ସୂଚିତ କରାଯାଇଥାଏ।

ମାନକ ବିଦ୍ୟୁତିର ସୁଗୁଣ (Merits of Standard Deviation):
(୧) ଏହାର ସଠିକ୍ ସଂଜ୍ଞା ଅଛି ଏବଂ ଏହା ଅଧ‌ିକ ପ୍ରତିନିଧୃତ୍ଵ ଅଟେ।
(୨) ଏହା ତଥ୍ୟାବଳୀର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ପର୍ଯ୍ୟବେସିତ।
(୩) ଏହା ପୁନଃ ବୀଜଗାଣିତିକ ବିଶ୍ଳେଣଷରେ ବ୍ୟବହାର କ୍ଷମ।
(୪) ଏହା ନମୁନା ପରିବର୍ତ୍ତନରେ ମାନକ ବିଚ୍ୟୁତି କମ୍ ପ୍ରଭାବିତ ହୋଇଥାଏ।
(୫) ଏହା ବିଚ୍ଛୁରଣ ପଦ୍ଧତିର ଏକ ଉତ୍ତମ ପରିମାପକ।

ମାନକ ବିଚ୍ୟୁତିର ଦୁର୍ଗୁଣ (Demerits of Standard Deviation):
(୧) ଅନେକ ଗାଣିତିକ ନମୁନା ସହିତ ଜଡ଼ିତ ଥିବାରୁ ଏହାକୁ ଆକଳନ କରିବା କଷ୍ଟସାଧ୍ୟ ହୋଇଥାଏ।
(୨) ଏହା ଚୂଡ଼ାନ୍ତ ମୂଲ୍ୟକୁ ଅଧିକ ଗୁରୁତ୍ଵ ଦେଇଥାଏ।
(୩) ଏହାର ପରିସର ସୀମିତ ହୋଇଥାରୁ ଏହା ଏକ ଉତ୍ତମ ପରିମାପକ ନୁହେଁ।

Question ୧୫।
ହାରାହାରି କ’ଣ ଗୋଟିଏ ଆଦର୍ଶ ହାରାହାରୀର ଗୁଣାବଳୀ ଆଲୋଚନା କର।
(What is an Average? Explain the qualities of a good average.)
Answer:
ପରିସଂଖ୍ୟାନ ବିଶ୍ଳେଷଣରେ କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତିର ପରିମାପ ଏକ ଆବଶ୍ୟକ ତଥା ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ସଂକ୍ଷିପ୍ତ ପରିମାପ ଅଟେ। କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତି କହିଲେ କୌଣସି ବିତରିତ ତଥ୍ୟାବଳୀର ସମସ୍ତ ମୂଲକୁ ପ୍ରତିନିଧୂତ୍ବ କରୁଥିବା ଗୋଟିଏ ସଂଖ୍ୟାକୁ ବୁଝାଇଥାଏ। ଯାହା ତଥ୍ୟାବଳୀର ବାରମ୍ବାରତା ବିତରଣର କେନ୍ଦ୍ରରେ ଅବସ୍ଥିତ ହୋଇଥାଏ। (It is a statistical device which studies the concentration of data around the central value, ସମୁଦାୟ ସମଷ୍ଟିଗତ ତଥ୍ୟର ଏହା ଏକ ପ୍ରତିରୂପ ମୂଲ୍ୟ ଅଟେ। ଏହାକୁ ଅବସ୍ଥିତିର ପରିମାପକ (Measures of Location) ବା ହାରାହାରି ବୋଲି କୁହାଯାଏ।

ହାରାହାରିର ସଂଜ୍ଞା (Definitions of an Average) :
ପରିସଂଖ୍ୟାନବିତ୍‌ମାନେ ହାରାହାରିର ବିଭିନ୍ନ ସଂଜ୍ଞା, ନିରୂପଣ କରିଛନ୍ତି।
ପରିସଂଖ୍ୟାନବିତ୍‌ମାନେ ହାରାହାରିର ବିଭିନ୍ନ ସଂଜ୍ଞା ନିରୂପଣ କରିଛନ୍ତି।

୧। କ୍ଲାର୍କଙ୍କ ମତରେ “ ସମୁଦାୟ ସଂଖ୍ୟାକୁ ବର୍ଣନା କରିବାପାଇଁ ଏକ ସଂଖ୍ୟା ଖୋଜିବାର ପ୍ରଚେଷ୍ଟାକୁ ହାରାହାରି କୁହାଯାଏ।
(According to Clark “Average is an attempt to find one single figure to describe the whoel of figures.”)

୨। ୟା-ଲୁନ୍-ଚୁଙ୍କ ମତରେ “ ଏକ ହାରାହାରି ସେହି ଅର୍ଥରେ ଏକ ସ୍ଵତନ୍ତ୍ର ମୂଲ୍ୟ, ଯାହାକି ବେଳେବେଳେ କ୍ରମରେ ଥ‌ିବା ସମସ୍ତ ବ୍ୟକ୍ତିଗତ ମୂଲ୍ୟଗୁଡ଼ିକ ବା କାରକଗୁଡ଼ିକୁ ପ୍ରତିନିଧୂତ୍ବ କରିବାକୁ ନିଯୁକ୍ତ ହୋଇଥାଏ ।’ According to Ya-Lun-chuo “An average is a typical value in the sense that it is some times employed to represent all the individual series of a variable.”

୩। ସଂପସନ ଏବଂ କାଫ୍‌କାଙ୍କ ମତରେ “ ଏକ କେନ୍ଦ୍ରୀୟ ଅଭିରୁଚି ପରିମାଣ ଏକ ସ୍ଵତନ୍ତ୍ର ପ୍ରକାରର ମୂଲ୍ୟ, ଯାହାର ଚତୁଃପାର୍ଶ୍ଵରେ ଅନ୍ୟାନ୍ୟ ସଂଖ୍ୟାଗୁଡ଼ିକ ଏକାଠି ହୋଇଥାନ୍ତି। ”According to Simpson and Kafka, “A measure of central tendency is a typucal value around which other figures congrgate.”

ହାରାହାରି ଆଭିମୁଖ୍ୟ (Objectives of studying averages) :
ବିଭିନ୍ନ ପାରିସାଂଖ୍ୟକ ପଦ୍ଧତି ମଧ୍ୟରେ ହାରାହାରି ବିଶେଷ ସ୍ଥାନ ଅଧିକାର କରିଥାଏ। ତେଣୁ ପ୍ରଫେସର ବାଉଲି ଏହାକୁ ହାରାହାରିର ଏକ ଏକ ବିଜ୍ଞାନ ବୋଲି ଅଭିହିତ କରିଛନ୍ତି। “Statistics is a science of an average”. ଏହାର ଆଭିମୁଖ୍ୟକୁ ନିମ୍ନୋକ୍ତ ମତେ ଆଲୋଚନା କରାଯାଇପାରେ।

1. ଜଟିଳ ତଥ୍ୟକୁ ଏହା ସରଳ ରୂପରେ ପ୍ରକାଶ କରିଥାଏ।
2. ଗୋଟିଏ ପ୍ରକାର ତଥ୍ୟ ସହିତ ଅନ୍ୟ ଏକ ତଥ୍ୟକୁ ତୁଳନା କରିବାରେ ସାହାଯ୍ୟ କରେ।
3. କେବଳ ମାତ୍ର ଏକ ନମୁନାରୁ ଏକ ଗୋଷ୍ଠୀ ବା ଉପାଦନମାନଙ୍କର ସମଷ୍ଟିକୁ ଜାଣିବାରେ ଏହା ସାହାଯ୍ୟ କରେ।
4. ଗାଣିତିକ ସଂପର୍କ ସ୍ଥାପନ ଓ ପରିସଂଖ୍ୟାନ ବିଶ୍ଳେଷଣ୍ଡର ହାରାହାରିର ଭୂମିକା ଅତ୍ୟନ୍ତ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ହୋଇଥାଏ।
5. ନୀତି ନିର୍ଦ୍ଧାରଣରେ ହାରାହାରି ସାହାଯ୍ୟ କରେ।

ଏକ ଆଦର୍ଶ ହାରାହାରିର ଲକ୍ଷଣ (Characteristics of an ideal average):-
୧। ସହଜ ବୋଧଗମ୍ୟତା ଓ ସହଜ ଗଣନା (Simple to understand and easy to calculate):- ସରଳ ବୋଧଗମ୍ୟତା ଏକ ଆଦର୍ଶ ହାରାହାରିର ପ୍ରଧାନ ଲକ୍ଷଣ ଅଟେ ! ସରଳ ଓ ସହଜ ବୋଧଗମ୍ୟତା ହେତୁ ଏହାର ଗଣନା ସହଜ ହୋଇଥାଏ ।

୨। ହାରାହାରିର ସଠିକ୍ ବାଖ୍ୟ ( Average should be rightly defined):- ସଠିକ୍ ଓ କର ବାଖ୍ୟ ଏକ ଆଦର୍ଶ ହାରାହାରିର ଅନ୍ୟ ଏକ ପ୍ରମୁଖ ଲକ୍ଷଣ। ଏହାଦ୍ଵାରା ବ୍ୟକ୍ତିଗତ ଚିନ୍ତା ଓ ମତାମତ ଏଡାଇବା ସମ୍ଭବ ହୋଇଥାଏ। ଏହାର ଅର୍ଥ କିମ୍ବା ସଂଜ୍ଞା ନେଇ କୌଣସି ପ୍ରକାର ବୃଦ୍ଧ ରହିବା ଉଚିତ ନୁହେଁ।

୩। ପୁନଃ ବୀଜଗାଣିତିକ ଓ ପାରିସାଂଖ୍ୟକ ପ୍ରତିପାଦନ କ୍ଷମତା (helpful for further algebric and statistical treatment):- ଏକ ଆଦର୍ଶ ବା ଉତ୍ତମ ହାରାହାରିର ବୀଜଗାଣିତିକ ପାରିସାଂଖ୍ୟକ ପ୍ରତିପାଦନ କ୍ଷମତା ଥିବା ଆବଶ୍ୟକ। ଏହା ନ ଥିଲେ ହାରାହାରି ସବୁ କ୍ଷେତ୍ରରେ ବ୍ୟବହାର ଉପଯୋଗୀ ହୋଇପାରେ ନାହିଁ।

୪। ଅନୁକ୍ରମର ସମସ୍ତ ବିଷୟ ଉପରେ ପର୍ଯ୍ୟବେସିତ ହୋଇଥବା ଉଚିତ (Should be based on all the items of a serics: ଏକ ଉତ୍ତମ ଓ ଆଦର୍ଶ ହାରାହାରି ନିଶ୍ଚିତ ଭାବେ ଅନୁକ୍ରମ ର ସମୟ ବିଷୟ ଉପରେ ପର୍ଯ୍ୟବେସିତ ହେବା ଉଚିତ। ଏହାଦ୍ଵାରା ହାରାହାରି ଅଧୂକ ପ୍ରତିନିଧୁଭିଭିକ ହୋଇପାରିବ।

୫। ଚରମ ସଂଖ୍ୟା ଦ୍ଵାରା ଅଯଥା ପ୍ରଭାବିତ ହେଉ ନଥ‌ିବ (Should not be unduly affected by extreme items): ଏକ ଅନୁକ୍ରମର ଚରମ ସଂଖ୍ୟା, ଯଥା ବୃହତ୍ ସଂଖ୍ୟା କିମ୍ବା କ୍ଷୁଦ୍ର ସଂଖ୍ୟା ଦ୍ଵାରା ଅଯଥା ପ୍ରଭାବିତ ହେଉନଥିବା ହାରାହାରିକୁ ଏକ ଉତ୍ତମ ବା ଆଦର୍ଶ ହାରାହାରି କୁହାଯାଏ ।

୬। ନମୁନା ଅସ୍ଥିରତା ଦ୍ବାରା ଅଧ‌ିକ ପ୍ରଭାବିତ ହେଉ ନଥିବା ଉଚିତ (Should not be aflected much by sampling fluctuations): ଏକ ଆଦର୍ଶ ହାରାହାରି ନମୁନା ଅସ୍ଥିରତା ଦ୍ବାରା ପ୍ରଭାବିତ ହେଉନଥୁବା ଉଚିତ ଅନ୍ୟ ଅର୍ଥରେ କହିଲେ ଏକ ଆଦର୍ଶ ହାରାହାରିର ନମୁନା ସ୍ଥାୟିତ୍ଵ ରହିବା। ଏକାନ୍ତ ଆବଶ୍ୟକ।

Question ୧୬।
ଗାଣିତିକ ମାଧ୍ଯମାନ କ’ଣ ? ଏହାର ଉପକାରିତା ଓ ଅପକାରିତା ଆଲୋଚନା କର। (What is Mean? Explai its merits and demerits.)
Answer:
ଗୋଟିଏ ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କର ହାରାହାରି ମାପକୁ ତଥ୍ୟାବଳୀର ମାମାନ କୁହାଯାଏ। କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତିର ଏହା ଏକ ସରଳ ପରିମାପକ। ଏଚ୍. ସେକ୍ରିଷ୍ଟଙ୍କ ମତରେ, ଗୋଟିଏ ମାଳାରେ ଥିବା ସମସ୍ତ ଲବ୍‌ଧାଙ୍କର ମୂଲ୍ୟର ସମଷ୍ଟିକୁ ସେମାନଙ୍କ ମୋଟ ସଂଖ୍ୟା ଦ୍ଵାରା ଭାଗ କଲେ ଯେଉଁ ସଂଖ୍ୟା ମିଳେ, ତାହା ଗାଣିତିକ ମାଧ୍ୟମାନ (arithmetic mean) ଅଟେ। The arithmetic mean of a series is the sum of the values of all items divided by the number of items. ଏହା ସାଧାରଣତଃ ଦ୍ଵାରା ସୂଚିତ ହୁଏ।

ଗାଣିତିକ ମାଧ୍ଯମାନର ଉପକାରିତା (Merits of Arithmetic mean): ଗାଣିତିକ ମାଧ୍ୟମାନର ଉପକରିତାକୁ ନିମ୍ନମତେ ଆଲୋଚନା କରାଯାଇପାରେ।

1. ଗାଣିତିକ ମାଷ୍ଟମାନ ଅନୁକ୍ରମର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ (Items) ଉପରେ ପର୍ଯ୍ୟବେସିତ ଅଟେ।
2. ଗାଣିତିକ ମାଧ୍ୟମାନକୁ ବୁଝିବା ଓ ଗଣନା କରିବା ସହଜ ଅଟେ।
3. ଗାଣିତିକ ମାଧ୍ୟମାନର ନମୁନା ସ୍ଥାୟିତ୍ଵ ରହିଥାଏ।
4. ଏହାର ପ୍ରବୃତି ସଂପୂର୍ଣ୍ଣ ବୀଜଗାଣିତିକ ଓ ଗାଣିତିକ ଅଟେ।
5. ଏହାର କଠୋର ଭାବେ ସଂଜ୍ଞାବୃତ କରାଯାଇଛି।
6. ଏହାର ପୁନଶ୍ଚ ବୀଜଗାଣିତିକ ଉପଯୋଗିତା ସମ୍ଭବ ଅଟେ।

ଗାଣିତିକ ମାଧ୍ଯମାନର ଅପକାରିତା। (Demerits of Arithmetic mean)

1. ମାଧ୍ଯମାନ ଚରମ ଲବ୍‌ଧାଙ୍କ (extreme value) ମାନଙ୍କଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ। ମାଧ୍ଯମାନର ଉର୍ଦ୍ଧ୍ୱମୁଖୀ ଅଭିନତି (Upward) ଥାଏ । ଯେଉଁଠାରେ ଲବ୍‌ଧାଙ୍କମାନଙ୍କ ସଂଖ୍ୟା କମ୍ ହୋଇଥାଏ ମାଧମାନ ସେଠାରେ ସେମାନଙ୍କ ଉପଯୁକ୍ତ ପ୍ରତିନିଧିତ୍ଵ କରିପାରେ ନାହିଁ।
2. ଅଧିକାଂଶ ସମୟରେ ଗାଣିତିକ ମାନ ବଣ୍ଟନମାଳାର ବାସ୍ତବ ଲବ୍‌ଧାଙ୍କରେ ନଥାଏ। ତେଣୁ ଏହାକୁ କାଳ୍ପନିକ ହାରାହାରି ବୋଲି କୁହାଯାଇଥାଏ।
3. କୌଣସି ତଥ୍ୟାବଳୀର ରାଶିମାଳାରେ ଗୋଟିଏ ଲବ୍‌ଧାଙ୍କ ନ ପାଇଲେ ମାଧ୍ୟମାନ ନିର୍ଣ୍ଣୟ ସମ୍ଭବପର ହୁଏ ନାହିଁ।
4. ତେକ ସମୟରେ ଗାଣିତିକ ମାଧ୍ୟମାନ ହାସ୍ୟାସ୍ ଉପସଂହାର ପ୍ରଦାନ କରିଥାଏ।
5. ଗୁଣବାଚକ ତଥ୍ୟାବଳୀ, ଯଥା- ମାନସିକ ଦକ୍ଷତା ଓ ସାଧୁତାର ପରିପ୍ରକାଶ ନିମିତ୍ତ ମାଧ୍ଯମାନର ଉପଯୋଗ ହୋଇପାରେନା। ଯେହେତୁ ଏହାର ସାଂଖ୍ୟକ ଅଭିବ୍ୟକ୍ତି ସମ୍ଭବପର ନୁହେଁ।

Question ୧୬।
୬୦ ଜଣ ଛାତ୍ରଛାତ୍ରୀଙ୍କର ନମ୍ବର ରେକର୍ଡ଼ କରାଯାଇଛି । ଯାହାର ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ଓ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ ନିର୍ଣ୍ଣୟ କର।
(Calculate the value of Quartile duration and co-efficient of Q.D.) of 60 students in a class.)

ନମ୍ବର (Marks)	୧୦	୨୦	୩୦	୪୦	୫୦	୬୦
ଛାତ୍ରଛାତ୍ରୀ ସଂଖ୍ୟା	୨	୮	୨୦	୨୨	୫	୩

Answer:

Question ୧୭।
ନିମ୍ନ ତଥ୍ୟାବଳୀର ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି ଓ ତାହାର ଗୁଣାଙ୍କ ନିରୂପଣ କର।
(Caculate the value of Quartile duration and its co-efficient.)

ନମ୍ବର (Marks)	୧-୧୦	୧୦ -୨୦	୨୦ – ୩୦	୩୦ – ୪୦	୪୦ – ୫୦
ଛାତ୍ରଛାତ୍ରୀ ସଂଖ୍ୟା(x) ୬	୧୫	୨୨	୧୮	୯

Answer:

: ଚତୁର୍ଥାଂଶକ ବିଚ୍ୟୁତି = ୯.୦୫ ଓ ଚତୁର୍ବିଂଶକ ବିଚ୍ୟୁତି ଗୁଣାଙ୍କ = ୦.୩୩।

Question ୧୮।
ନିମ୍ନୋକ୍ତ ୧୦ ଜଣ ପିଲାଙ୍କର ବୟସରୁ ମାଧ୍ୟ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କର। (Determine the value of mean deviation.)
X = ୧୦, ୧୧, ୧୨, ୧୩, ୧୪, ୧୫, ୧୬, ୧୭, ୧୮, ଓ ୧୯।
Answer:
ପ୍ରଥମେ ରାଶିମାଳାର ମାଧ୍ୟମାନ ଓ ପରେ ମାଧ୍ୟମାନରୁ ଲବ୍‌ଧାମାନଙ୍କର ବିଦ୍ୟୁତିର ପରମ ମାନ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ।

ମାଧ୍ୟ ବିଦ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ

X	|x-x̄| |d|
୧୦	୫
୧୧	୪
୧୨	୩
୧୩	୨
୧୪	୧
୧୫	୦
୧୬	୧
୧୭	୨
୨୦	୫
୨୨	୭
Σx = ୧୫୦	Σd = ୩୦

ମାଧ୍ୟ ବିଦ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ

କ୍ର.ନଂ	ଲବଙ୍କ	|x-Md| କିମ୍ବା |d|
୧	୧୦	୪.୫
୨	୧୧	୩.୫
୩	୧୨	୨.୫
୪	୧୩	୧୫
୫	୧୪	୦.୫
୬	୧୫	୦.୫
୭	୧୬	୧.୫
୮	୧୭	୨.୫
୯	୨୦	୫.୫
୧୦	୨୨	୭.୫
		Σ|d| = ୩ ୦ .୦

ମଧ୍ୟମାର ମାଧ୍ୟ ବିଚ୍ୟୁତି MD = \(\frac{\sum|\mathrm{x}-\mathrm{Md}|}{\mathrm{n}}\)
= ୩.୦
∴ ମାଧ୍ୟ ବିଚ୍ୟୁତି = ୩

Question ୧୯।
ନିମ୍ନରେ ୪୫ ଜଣ ପିଲାଙ୍କର ବୟସ ପ୍ରଦତ୍ତ ହୋଇଛି। ତାହାର ମାଧ ବିଚ୍ୟୁତି ମାପ କର।
(Determine the value of mean deviation.)

X	୧୦	୧୫	୨୦	୨୫	୩୦
F	୫	୧୦	୨୦	୬	୪

Answer:

X	F	CF	|d| = |X – ୨୦|	F|d|
୧୦	୫	୫	୧୦	୫୦
୧୫	୧୦	୧୫	୫	୫୦
୨୦	୨୦	୩୫	୦	୦
୨୫	୬	୪୧	୫	୩୦
୩୦	୪	୪ ୫	୧୦	୪୦
	Σf = ୪ ୫		Σ|d| = ୩୦	ΣF|d| = ୧୭୦

Question ୨୦।
ନିମ୍ନଲିଖତ ତଥ୍ୟାବଳୀର ମାଧ୍ୟ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କର।
(Determine the mean deviation of the following F.D.)

X	୦ – ୧୦	୧୦ -୨୦	୨୦ – ୩୦	୩୦ – ୪୦	୪୦ – ୫୦	୫୦ – ୬୦
ବାରମ୍ବାରତାF	୨	୬	୧୫	୨୦	୧୨	୫

ସମାଧାନ: ମାଧ୍ୟ ବିଚ୍ୟୁତି ସାରଣୀ

X	ବାରମ୍ବାରତାF	CF	ମଧ୍ୟବିନ୍ଦୁ m	ବିଦ୍ୟୁତିର ପରମମାନ |d| = |m–୩୩.୫|	F |d|
୦ – ୧୦	୨	୨	୫	୨୮. ୫	୫୭
୧୦ -୨୦	୬	୮	୧୫	୨୮. ୫	୧୧୧.୦
୨୦ – ୩୦	୧୫	୨୩	୨୫	୮. ୫	୧୨୭.୫
୩୦ – ୪୦	୨୦	୪୩	୩୫	୧.୫	୩୦
୪୦ – ୫୦	୧୨	୫୫	୪୫	୧୧.୫	୧୦୭. ୫
୫୦ – ୬୦	୫	୬୦	୫୫	୨୧.୫	୧୦୭.୫
	ΣF = ୬ ୦				୫୭୧

Question ୨୧।
ନିମ୍ନ ତଥ୍ୟାବଳର ମାନକ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କର। (Determine the value of standard.)
୧୦, ୧୨, ୧୪, ୧୬, ୧୮, ୨୦, ୨୨
Answer:

Question ୨୨।
ନିମ୍ନଲିଖତ ତଥ୍ୟାଗ ର ମାନକ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କରାଯାଇଛି।
(Determine the vlaue of standard deviation.)
ସମାଧାନ :

Question ୨୩।
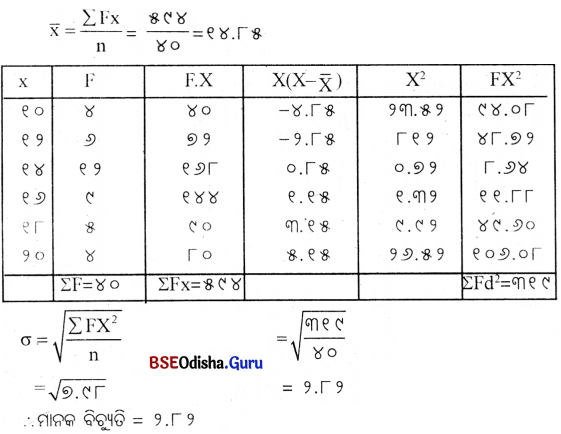
ନିମ୍ନ ବିତରଣର ମାନକ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କର।
(Determine the value of standard deviation.)

x	f
୧୦	୪
୧୨	୬
୧୪	୧୨
୧୬	୯
୧୮	୫
୨୦	୪

Answer:

Question ୨୪।
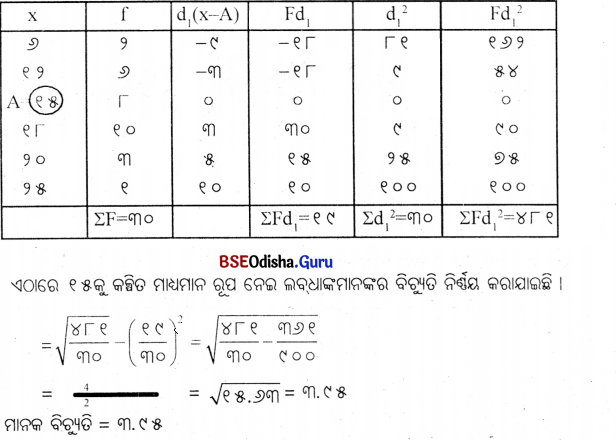
ନିମ୍ନ ବିତରଣର ମାନକ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କର। (Determine’ the value of standard deviation.)

x	f
୬	୨
୧୨	୬
୧୫	୮
୧୮	୧୦
୨୦	୩
୨୫	୧

ସମାଧାନ : ମାନକ ବିଚ୍ୟୁତି ସାରଣୀ

Question ୨୫।
ନିମ୍ନ ବିତରଣର ମାନକ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କର।
(Determine the value of standard deviation.)

x	୦ – ୧୦	୧୦ -୨୦	୨୦ – ୩୦	୩୦ – ୪୦	୪୦ – ୫୦
f	୪	୪	୧୨	୮	୨

Answer:

x	f	m	Fm	d(m -୨୫)	X2	F2
୦ – ୧୦	୪	୫	୨୦	– ୨୦	୪୦୦	୧୬୦୦
୧୦ – ୨୦	୪	୧୫	୬୦	– ୧୦	୧୦୦	୪୦୦
୨୦ – ୩୦	୧୨	୨୫	୩୦୦୦	୦	୦	୦
୩୦ – ୪୦	୮	୩୫	୨୮୦	୧୦	୧୦୦	୮୦୦
୪୦ – ୫୦	୨	୪୫	୯୦	୨୦	୪୦୦	୮୦୦
	ΣF = ୩୦	ΣFm = ୭୫୦	୭୫୦			Σd2 = ୩୬୦୦

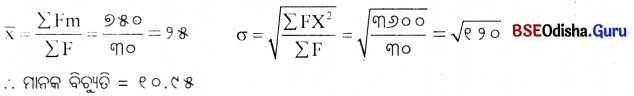
Question ୨୬।
ମାନକ ବିଚ୍ୟୁତି ନିର୍ଣ୍ଣୟ କର। (Determine the value S.D.)

x	୦ – ୧୦	୧୦ -୨୦	୨୦ – ୩୦	୩୦ – ୪୦	୪୦ – ୫୦	୫୦ – ୬୦
f	୨	୫	୮	୧୪	୧୦	୧

Answer:

Question ୨୭।
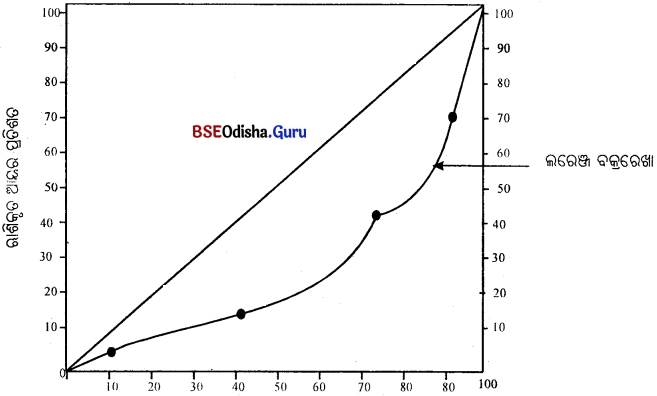
ଲରେଞ୍ଜ ବକ୍ରରେଖା (Lorenz curve)
(Explain the Lorenz Curve.)
Answer:
ବିଚ୍ଛୁରତାର ବିଭିନ୍ନ ଗାଣିତିକ ପରିମାପ ଉପନ୍ୟୁକ୍ତ ପୃଷ୍ଠାମାନଙ୍କରେ ଆଲୋଚିତ ହୋଇଛି। ଏହାର ଏକ ଜ୍ୟାମିତିକ ପରିମାପ ପଦ୍ଧତି ରହିଛି, ଯାହା ହେଉଛି ଲରେଞ୍ଜ ବକ୍ରରେଖା। ମାକ୍‌ସ ଓ ଲରେଞ୍ଜଙ୍କ ଦ୍ଵାରା ସୃଷ୍ଟ ବିଚ୍ଛୁରଣର ଜ୍ୟାମିତିକ ପରିମାପ ଲରେଞ୍ଜ ବକ୍ରରେଖା ଭାବେ ପରିଚିତ। ସେ ପ୍ରଥମେ ସମ୍ପଦର ବଣ୍ଟନରେ ଥବ। ବୈଷମ୍ୟତ। ଅନୁଧ୍ୟାନ କରିବା ପାଇଁ ଏହି ପଦ୍ଧତି ପ୍ରୟୋଗ କରିଥିଲେ। ପରବର୍ତ୍ତୀ ପର୍ଯ୍ୟାୟରେ ଏହି ପଦ୍ଧତି ଲାଭ, ମଜୁରୀ, ଆୟ ଇତ୍ୟାଦିର ପରିବଣ୍ଟନ ର ପରିବର୍ତ୍ତନକୁ ଅଧ୍ୟୟନ କରିବାରେ ବ୍ୟବହୃତ ହେଉଛି। ଏହା ହେଉଛି ଏକ ରାଶିକୃତ ଶତାଂଶ ବକ୍ରରେଖା, ଯାହାର ଅଙ୍କନ ପାଇଁ ନିମ୍ନଲିଖତ ପଦକ୍ଷେପମାନ ନିଆଯାଏ।

୧। ପ୍ରଥମେ ଲବ୍‌ଧାଙ୍କ ସବୁର ରାଶିକୃତ ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କରାଯାଏ।
୨। ମୋଟ ରାଶିକୃତ ମୂଲ୍ୟକୁ ୧୦୦ ବୋଲି ଗ୍ରହଣ କରି ଅନ୍ୟ ସମସ୍ତ ରାଶିକୃତ ଲବ୍‌ଧାଙ୍କର ଶତାଂଶ ନିର୍ଣ୍ଣୟ କରାଯାଏ।
୩। ସେହିପରି ବାରମ୍ବାରତା ସବୁର ରାଶିକୃତ ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କରି ମୋଟ ବାରମ୍ବାରତାକୁ ୧୦୦ ବୋଲି ଗ୍ରହଣ କରି ଅନ୍ୟ ସମସ୍ତ ରାଶିକୃତ ବାରମ୍ବାରତାର ଶତାଂଶ ନିରୂପଣ କରିବାକୁ ହୁଏ।
୪। ଆନୁଭୂମିକ ଅକ୍ଷରେ ରାଶିକୃତ ବାରମ୍ବାରତାର ଶତାଂଶ ଓ ଉଲମ୍ବ ଅକ୍ଷରେ ରାଶିକୃତ ଲବ୍ଧଧାଙ୍କର ଶତାଂଶ ଅବସ୍ଥାପିତ କରାଯାଏ।
୫। ୦ (୦,୦) ଏବଂ ୧ (୧୦୦,୧୦୦) ବିନ୍ଦୁ ଦ୍ଵୟକୁ ଯୋଗକରି ଏକ କର୍ଷ ଅଙ୍କନ କରିବାକୁ ପଡ଼େ, ଯାହାକୁ ସମବଣ୍ଟନ ରେଖା କୁହାଯାଏ, ଏହା ଲେଖଚିତ୍ରର ମୂଳବିନ୍ଦୁରେ ୪୫୦ କୋଣ ଅଙ୍କନ କରିଥାଏ।
୬। ରାଶିକୃତ ଲବ୍‌ଧାଙ୍କର ଶତାଂଶ ଓ ରାଶିକୃତ ବାରମ୍ବାରତାର ଶତାଂଶ ସବୁର କ୍ରମିକ ଯୋଡିସବୁକୁ ଲେଖବିନ୍ଦୁ ଆକାରରେ ଗ୍ରାଫ୍‌ରେ ଅବସ୍ଥାପିତ କରାଯାଏ।
୭। ସେହି ଲେଖବିନ୍ଦୁସବୁକୁ ଏକ ସାବଲୀଳ ରେଖାଦ୍ଵାରା ସଂଯୋଗ କରି ଲରେଞ୍ଜ, ବକ୍ରରେଖା ଅଙ୍କନ କରାଯାଏ।
୮। ଲରେଞ୍ଜ ବକ୍ରରେଖା ସମବଣ୍ଟନ ରେଖାର ନିକଟବର୍ତ୍ତୀ ହେଲେ ବିଜୁରଣ କମ୍ ଓ ଦୂରବର୍ତ୍ତୀ ହେଲେ ବିଚ୍ଛୁରଣ ଅଧ‌ିକ ହୋଇଥାଏ। ଏକାଧ୍ଵକ ବିତରଣର ତୁଳନାତ୍ମକ ବିଶ୍ଳେଷଣ ପାଇଁ ଗୋଟିଏ ଗ୍ରାଫ୍‌ରେ ଏକାଧିକ ଲରେଞ୍ଜ ବକ୍ର ଅଙ୍କନ କରାଯାଇପାରେ।

Question ୨୮।
ମାନକ ବିବୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ କର।
(Determine the value of S.D.)

x	୦ – ୧୦	୧୦ -୨୦	୨୦ – ୩୦	୩୦ – ୪୦	୪୦ – ୫୦	୫୦ – ୬୦
f	୨	୫	୮	୧୪	୧୦	୧

Answer:
ସୋପାନ ବିଚ୍ୟୁତି ପ୍ରଣାଳୀରେ : ମାନକ ବିଚ୍ୟୁତିର ମୂଲ୍ୟ ନିର୍ଦ୍ଧାରଣ

x	F	m	d(m – ୨୫)	d1 = d/୧୦	d12	Fd1>	Fd12
୦-୧	୨	୫	-୨୦	-୨	୪	-୪	୮
୧୦-୨୦	୫	୧୫	-୧୦	-୧	୧	-୫	୫
୨୦-୩୦	୮	୨୫	୦	୦	୦	୦	୦
୩୦-୪୦	୧୪	୩୫	୧୦	୧	୧	୧୪	୧୪
୪୦-୫୦	୧୦	୪୫	୨୦	୨	୪	୨୦	୪୦
୫୦-୬୦	୧	୫୫	୩୦	୩	୯	୩	୯
	ΣF = ୪୦						Σfd12 = ୭୬

Question ୨୯।
ନିମ୍ନରେ ଗୋଟିଏ ଗ୍ରାମର ବିଭିନ୍ନ ପରିବାରର ଆୟ ପ୍ରଦତ୍ତ ହୋଇଛି। ଲରେଞ୍ଜ ବକ୍ରରେଖା ଅଙ୍କନ କରି ସେହି ଗ୍ରାମରେ ଆୟ ବଣ୍ଟନରେ ବୈଷ୍ୟମତା ଦର୍ଶାଅ।
(Construct a Lorenz Curve of the following Series.)

ମାସିକ ଆୟ (ହଜାର ଟଙ୍କାରେ)	ଗ୍ରାମର ପରିବାର ସଂଖ୍ୟା
୫	୫
୧୦	୧୩
୧୫	୧୫
୨୦	୫
୨୫	୨

Answer:

ମାସିକ ଆୟ ( ହଜାରେ ଟଙ୍କାରେ )	ରାଶିକୃତ ଆୟ	ରାଶିକୃତ ଆୟର ପ୍ରତିଶତ	ଗ୍ରାମର
			ପରିବାର	ରାଶିକୃତ ପରିବାର ସଂଖ୍ୟାର	ରାଶିକୃତ ପରିବାର ସଂଖ୍ୟାର
୫	୫	୫	୫	୫	୫
୧୦	୧୫	୧୫	୧୩	୧୮	୧୮
୧୫	୩୦	୩୦	୧୫	୩୩	୩୩
୨୦	୫୦	୫୦	୧୦	୪୩	୪୩
୨୫	୭୫	୭୫	୫	୪୮	୪୮

ଏଠାରେ ଲରେଞ୍ଜ ବକ୍ରରେଖା ସମବଣ୍ଟନ ରେଖାଠାରୁ ଅଧିକ ଦୂରତାରେ ଥିବାରୁ ବିଜୁରଣର ମାତ୍ରା ଅଧିକ ବୋଲି ପ୍ରମାଣିତ।

Question ୩୦।
ମଧ୍ୟମା (Median)ଆଲୋଚନା କର। (Explain median.)
Answer:
ମଧ୍ୟମା ଏକ ଅବସ୍ଥାପିତ ହାରାହାରି। ଏହା କେନ୍ଦ୍ରୀୟ ଶ୍ରବଣତା ପରିମାପର ଅନ୍ୟ ଏକ ପରିମାପକ ଅଟେ। ସାନରୁ ବଡ କ୍ରମରେ ବା ବଡରୁ ସାନ କ୍ରମେ ମୁଦ୍ରିତ ହୋଇଥିବା ଏକ ଅନୁକ୍ରମର ସଂଖ୍ୟାଗୁଡିକୁ ସମାନ ଦୁଇଭାଗରେ ଅର୍ଥନୀତି ସମ୍ପର୍କିତ ପରିସଂଖ୍ୟାନ ବିଭାଜିତ କରୁଥ‌ିବା ଉପାଦାନର ମୂଲ୍ୟକୁ ମଧ୍ୟମା (Median)କୁହାଯାଏ। ସାଧାରଣ ଅର୍ଥରେ କହିଲେ ଏକ ବିତରଣମାଳାର ମଧ୍ୟ ଭାଗରେ ଥିବା ମାପକକୁ ମଧ୍ୟମା କୁହାଯାଏ। ଏହା ଅନୁକ୍ରମକୁ ସମାନ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରିଥାଏ। ଗୋଟିଏ ଅଂଶର ମୂଲ୍ୟ ମଧ୍ୟମା ମୂଲ୍ୟଠାରୁ ଅଧିକ ଏବଂ ଅନ୍ୟ ଅଂଶର ମୂଲ୍ୟ ମଧ୍ୟମା ମୂଲ୍ୟଠାରୁ କମ୍ ହୋଇଥାଏ। ହୋରାସ୍ ସିକ୍ରିଷ୍ଟାଙ୍କ ମତରେ, “ଏକ ଅନୁକ୍ରମର ମଧ୍ୟମା ସେହି ବିଷୟର ପ୍ରକୃତ ବା ଆନୁମାନିକ ମୂଲ୍ୟ ଯେତେବେଳେ କି ଏକ ଅନୁକ୍ରମ ବଡସାନ କ୍ରମରେ ମୁଦ୍ରିତ ହୋଇଥାଏ। ଯାହାକି ବିତରଣକୁ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରିଥାଏ।”

According to Horace Secrist, “Median of a series is the value of the item, actual or estimated when a series is arranged in order of magnitude which divides the distribution into two parts.”

ମଧ୍ୟମାର ଉପକାରିତା (Merits of median):-
୧। ମଧ୍ୟମା ଏକ ସହଜ, ସରଳ ଓ ବୋଧଗମ୍ୟ ହାରାହାରି ଅଟେ।
୨। ମଧ୍ୟମାକୁ ଗଣନା କରିବା ଓ ବୁଝିବା ସହଜ ଅଟେ।
୩। ଗୁଣାତ୍ମକ ତଥ୍ୟକୁ ଅଧ୍ୟୟନ କରିବାରେ ମଧ୍ୟମା ଅଧୂକ ଉପଯୋଗୀ ଅଟେ।
୪। ମଧ୍ୟମା ଅନୁକ୍ରମର ଚରମ ଲବ୍‌ଧାଙ୍କ ଦ୍ବାରା ପ୍ରଭାବିତ ହୁଏ ନାହିଁ।
୫। ମଧ୍ୟମାର ମୂଲ୍ୟକୁ ଗ୍ରାଫ ମାଧ୍ୟମରେ ପ୍ରଦର୍ଶିତ କରାଯାଇପାରିବ।
୬। ଧାରାବାହିକ କ୍ରମରେ ଅସମାନ ଶ୍ରେଣୀ ଅନ୍ତର ଥିଲେ ସେଗୁଡ଼ିକୁ ସମାନ ନକରି ମଧ୍ୟ ମଧ୍ଯମାକୁ ଗଣନା କରାଯାଇପାରିବ।

ମଧ୍ୟମାର ଅପକାରିତା (Demerits of median):
୧। ମଧ୍ୟମା ଏକ ଅବସ୍ଥାପିତ ହାରାହାରି ହୋଇଥିବାରୁ ଏହା ଅନୁକ୍ରମର ପ୍ରତ୍ୟେକ ରାଶି ଉପରେ ପର୍ଯ୍ୟବେସିତ ନୁହେଁ।
୨। ମଧ୍ୟମାର ପୁନଶ୍ଚ ବୀଜଗାଣିତିକ ପ୍ରତିପାଦନ କ୍ଷମତା ନଥାଏ।
୩। ମଧ୍ୟମା ନମୁନା ଅସ୍ଥିରତା ଦ୍ୱାରା ଅଧିକ ପ୍ରଭାବିତ ହୋଇଥିବାରୁ ଏହାର ଖୁବ୍ ନମୁନା ସ୍ଥିରତା (sampling stability) ରହିଥାଏ। ତେଣୁ ଏହାର ମୂଲ୍ୟ ଅସ୍ଥିର।
୪। ମଧ୍ୟମା ଗଣନା ସମୟରେ ତଥ୍ୟଗୁଡ଼ିକୁ ସାନରୁ ବଡ ବା ବଡରୁ ସାନ କ୍ରମରେ ସଜାଡିବାର ଆବଶ୍ୟକତା ରହିଛି, ଯାହା ଅତ୍ୟନ୍ତ ଜଟିଳ କାର୍ଯ୍ୟ ଅଟେ।
୫1 ଏକ ନିରବଚ୍ଛିନ୍ନ ଅନୁକ୍ରମରେ ମଧ୍ୟମା ଗଣନା କଲାବେଳେ କଳ୍ପନା କରାଯାଏ ଯେ ପେସନଃପୁନ୍ୟ ଶ୍ରେଣୀ ଅନ୍ତରଗୁଡ଼ିକ ମଧ୍ୟ ସମାନଭାବେ ବାଣ୍ଟି ହୋଇ ରହିଥାଏ, ଯାହାକି ସବୁ ସମୟରେ ସତ ହୋଇନଥାଏ।

Question ୨୮।
ଗରିଷ୍କକ (Mode) ଆଲୋଚନା କର। (Explain mode.)
Answer:
କୌଣସି ତଥ୍ୟାବଳୀରେ ଯେଉଁ ଲବ୍‌ଧାଙ୍କ ସର୍ବାଧ‌ିକ ଥର ଆବିର୍ଭୂତ ହୋଇଥାଏ, ତାହାକୁ ଗରିଷ୍ଠକ (Mode) କୁହାଯାଏ। ଫରାସୀ ଶବ୍ଦ ଲାମୋଡ (L.amode)ରୁ ଇଂରାଜୀ ଶବ୍ଦ (Mode) ବା ଗରିଷ୍ଠକ ଶବ୍ଦ ଆସିଛି। Mode is the value which occurs most frequently in a distribution, ବଣ୍ଟନମାଳାରେ ଏହା ଏକ ସାଧାରଣ ଲବ୍‌ଧାଙ୍କ ଅଟେ। ଏହାକୁ ବିତରଣମାଳାର ରୁଚିପୂର୍ଣ୍ଣ ମୂଲ୍ୟ କୁହାଯାଏ। ସମୟ ସମୟରେ ଦୁଇଟି ଲବକଂଙ୍କର ସମାନ ଓ ସର୍ବାଧ‌ିକ ବାରମ୍ବାର ଥାଏ। ଏହାକୁ Biodal ବା ଦ୍ବିଗରିଷ୍ଠକ ବଣ୍ଟନ କୁହାଯାଏ ।ସେହିଭଳି ଯଦି ତିନୋଟି ଗରିଷ୍ଠକ ଥାଏ ତାହାକୁ ତ୍ରିଗରିଷ୍ଠକ Trimodal ଏବଂ ତିନିରୁ ଅଧ‌ିକ ଗରିଷ୍ଠକ ଥିଲେ ତାହାକୁ ବହୁ ଗରିଷ୍ଠକ Multimodal ବଣ୍ଟନ କୁହାଯାଏ। ଯଦି କେବଳ ଗୋଟିଏ ଲବ୍‌ଧାଙ୍କର ବାରମ୍ବାରତା ସର୍ବାଧିକ ତାହାକୁ ଏକକ ଗରିଷ୍ଠକ ବଣ୍ଟନ (Unimodal distribution) କୁହାଯାଏ।

ଗରିଷ୍ଠକର ସଂଜ୍ଞା (efinitions of mode):
କ୍ରକ୍‌ଟନ୍‌ ଏବଂ କାଓ ଡେନଙ୍କ ମତରେ, “ଏକ ବିତରଣର ଗରିଷ୍ଠକ ଏକ ବିନ୍ଦୁରେ ଥିବା ଯାହାର ଚତୁଃପାର୍ଶ୍ବରେ ଲବ୍‌ଧାଙ୍କ ବା ସଂଖ୍ୟା ଗୁଡ଼ିକ ସର୍ବାଧ‌ିକ, ଭାବେ ଘନୀଭୂତ ହୋଇଥାନ୍ତି ମୂଲ୍ୟର ଏକ ସ୍ଵତନ୍ତଅ ପ୍ରକାର ଭାବେ ପରିଚିତ ହୋଇଥାଏ ।”

ଗରିଷ୍ଠକର ଉପକାରିତା (merits of mode):
୧। ତଥ୍ୟାବଳୀର ବାରମ୍ବାରତାକୁ ନିରୀକ୍ଷଣ କରି ସହଜରେ ଗରିଷ୍ଠକ ନିରୂପଣ କରାଯାଇପାରେ।
୨। ଚରମ ଲବ୍‌ଧାଙ୍କମାନଙ୍କ ଦ୍ବାରା ଗରୁଷ୍ପକ ପ୍ରଭାବିତ ହୁଏ ନାହିଁ।
୩। ଅସମାନ ସଂଭାଗଯୁକ୍ତ ବଣ୍ଟନରେ ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ କରିବାରେ କୌଣସି ଅସୁବିଧା ହୁଏ ନାହିଁ।

ଗରିଷ୍ଠକର ଅପକାରିତା (demerits of mode) :
୧। ବଣ୍ଟନର ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ବାରମ୍ବାରତା ସମାନ ହେଲେ ଗରିଷ୍ଠକ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ ନାହିଁ।
୨। ବଣ୍ଟନର ସମସ୍ତ ଲବ୍‌ଧାଙ୍କ ଉପରେ ଗରିଷ୍ପକ ପର୍ଯ୍ୟବେସିତ ନୁହେଁ ଏବଂ ଏଡା ଚୟନ ତ୍ରୁଟି ଦ୍ବାରା ପ୍ରଭାବିତ ହୋଇଥାଏ।
୩। ଗରିଷ୍ଠକ କେନ୍ଦ୍ରୀୟ ପ୍ରବୃତ୍ତିର ଏକ ଅନିଶ୍ଚିତ ଓ ଅବାନ୍ତର ପରିମାପକ ଅଟେ।