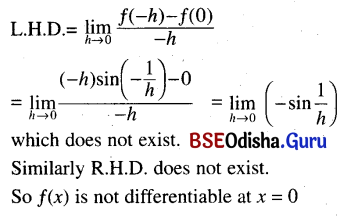CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Ex 14(f)

Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 14 Limit and Differentiation Ex 14(f) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Exercise 14(f)

Differentiate.

Question 1.
x⁸ + x⁷
Solution:
Let  y = x⁸ + x⁷
Then \(\frac{d y}{d x}\) = 8x⁷ + 7x⁶

Question 2.
x^5/3 – x^1/2
Solution:
Let y = x^5/3 – x^1/2
\(\frac{d y}{d x}=\frac{5}{3} x^{\frac{2}{3}}-\frac{1}{2} x^{-\frac{1}{2}}\)

Question 3.
x³ – 5x
Solution:
Let y = x³ – 5x
Then \(\frac{d y}{d x}\) = 3x² – 5

Question 4.
√x + \(\frac{1}{\sqrt{x}}-\sqrt[3]{x^2}\)
Solution:
Let y = √x + \(\frac{1}{\sqrt{x}}-\sqrt[3]{x^2}\)
= \(x^{\frac{1}{2}}+x^{-\frac{1}{2}}-x^{\frac{2}{3}}\)
⇒ \(\frac{d y}{d x}=\frac{1}{2} x^{\frac{-1}{2}}-\frac{1}{2} x^{\frac{-3}{2}}-\frac{2}{3} x^{\frac{-1}{3}}\)

Question 5.
x² + 2x – sin x + 5
Solution:
x² + 2x – sin x + 5
\(\frac{d y}{d x}\) = 2x + 2 – cos x

Question 6.
\(\frac{1}{2} x^{\frac{1}{2}}+\frac{1}{3} x^{\frac{1}{3}}\)
Solution:
\(\frac{1}{2} x^{\frac{1}{2}}+\frac{1}{3} x^{\frac{1}{3}}\)
\(\frac{d y}{d x}=\frac{1}{4} x^{\frac{-1}{2}}+\frac{1}{9} x^{\frac{-2}{3}}\)

Question 7.
ax² + b tan x + ln x³
Solution:
ax² + b tan x + ln x³
\(\frac{d y}{d x}\) = 2ax + b sec² x + \(\frac{3}{x}\)

Question 8.
√x(√x + 1)
Solution:
Let y = √x(√x + 1) = \(x+x^{\frac{1}{2}}\)
\(\frac{d y}{d x}=1+\frac{1}{2} x^{\frac{-1}{2}}\)

Question 9.
(x – 1)²
Solution:
Let y = (x – 1)²
Then \(\frac{d y}{d x}\) = 2(x – 1)

Question 10.
(x² – x + 2)²
Solution:
Let y = (x² – x + 2)²
\(\frac{d y}{d x}\) = 2(x² – x + 2) × \(\frac{d}{d x}\)(x² – x + 2)
= 2(x² – x + 2)(2x – 1)

Question 11.
x sin x – \(\frac{e^x}{1+x^2}\)
Solution:

Question 12.
tan 2x + sec 2x
Solution:

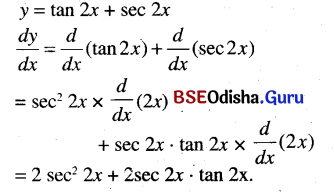
Question 13.
\(\frac{x^2}{x+1}-\frac{x}{1-x}\)
Solution:

Question 14.
\(\frac{\sqrt{x}-1}{\sqrt{x}+1}\)
Solution:

Question 15.
\(\frac{\tan x-\cos x}{\sin x \cos x}\)
Solution:

Question 16.
\(\left(\frac{x-1}{x+1}\right)^2\)
Solution:

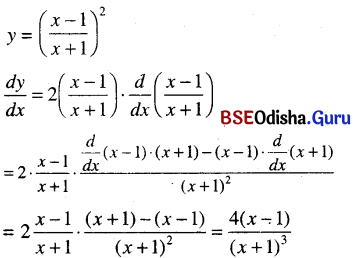
Question 17.
x³ (1 + x)(2 – x)
Solution:

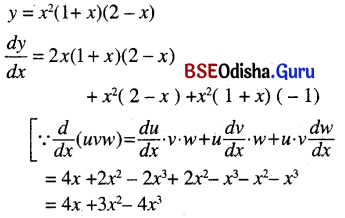
Question 18.
x₃ (sin x) e^{4 ln x}
Solution:

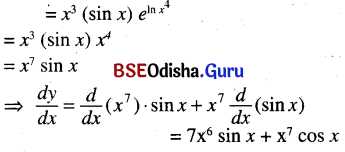
Question 19.
\(\frac{1}{\sqrt{x}}\) + x ln x³
Solution:

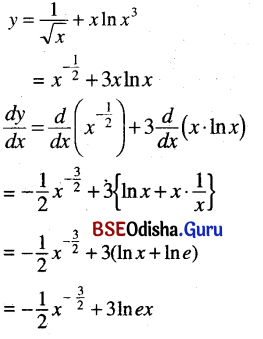
Question 20.
x² log₂ x + sec x
Solution:

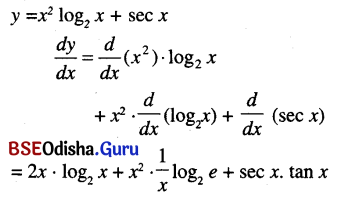
Question 21.
\(\frac{x^2-1}{x^3+1}\)
Solution:

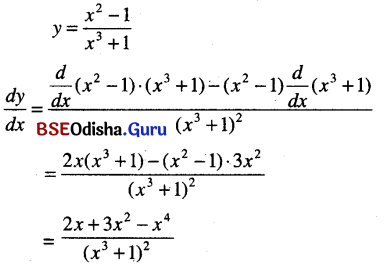
Question 22.
(x³ + 1)(3x² + 2x – 7)
Solution:

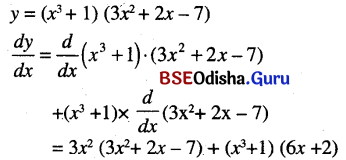
Question 23.
cot x – sec x – log₁₀ x
Solution:
\(\frac{d y}{d x}\) = -cosec ² x – sec x. tan x – \(\frac{1}{x} \log _{10} e\)

Question 24.
\(\frac{1-\cos x}{1+\cos x}\)
Solution:

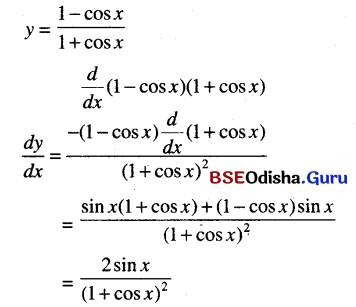
Question 25.
\(\frac{1-\tan x}{1+\tan x}\)
Solution:

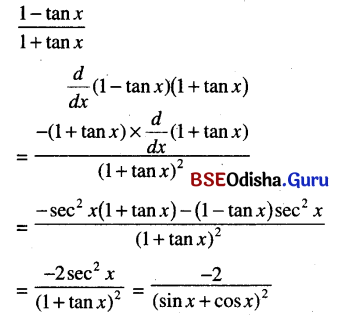
Question 26.
\(\frac{\left[x^{\frac{3}{5}}-2 e^2 \ln x+\ln ^{\frac{2}{3}}\right]}{(1+x)}\)
Solution:

Question 27.
cosec x + cot x
Solution:
Let y = cosec x + cot x
\(\frac{d y}{d x}\) = -cosec x. cot x – cosec ² x

Question 28.
tan² x + sec² x
Solution:
Let y = tan² x + sec² x
\(\frac{d y}{d x}\) = 2 tan x. \(\frac{d}{d x}\)(tan x) + 2 sec x \(\frac{d}{d x}\)(sec x)
= 2 tan x. sec² x + 2 sec² x. tan x
= 4 sec² x tan x

Question 29.
tan² x + a^x
Solution:
tan² x + a^x
\(\frac{d y}{d x}\) = 2 tan x. sec² x + a^x. ln a

Question 30.
sin² x + x ln x
Solution:
sin² x – x ln x

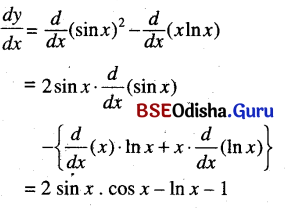
Question 31.
cos² x + e^x cos x
Solution:

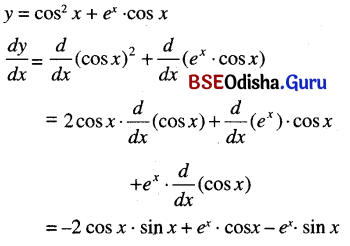
Question 32.
\(\frac{a^x-b^x}{x}\)
Solution:

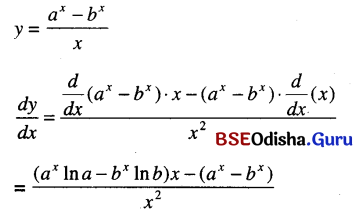
Question 33.
\(\frac{e^x+e^{-x}}{x^2+1}\)
Solution:

Question 34.
\(\frac{\ln x}{x^2}\)
Solution:

Question 35.
Show that f(x) = \(\left\{\begin{array}{l}
x \sin \frac{1}{x}, x \neq 0 \\
0, x=0
\end{array}\right.\) is not differentiable x = 0
Solution:
Differentiability