CHSE Odisha Class 11 Math Solutions Chapter 6 Complex Numbers and Quadratic Equations Ex 6(a)

Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 6 Complex Numbers and Quadratic Equations Ex 6(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 6 Complex Numbers and Quadratic Equations Exercise 6(a)

Question 1.
Multiply (2√-3 + 3√-2) by (4√-3 – 5√-2)
Solution:
(2√-3 + 3√-2) by (4√-3 – 5√-2)
= (2√3i + 3√2i) (4√3i – 5√2i)
= i² (2√3 + 3√2) (4√3 – 5√2)
= – 1(24 – 10√6 + 12√6 – 30)
= – 1(- 6 + 2√6) = 6 – 2√6

Question 2.
Multiply (3√-7 – 5√-2) (3√-2 + 5√-2)
Solution:
(3√-7 – 5√-2) (3√-2 + 5√-2)
= (3√7i – 5√-2i) (3√2i + 5√2i)
= i² (3√7- 5√2) (3√2 + 5√2)
= (- 1)8√2(3√7 – 5√2 )
= – 24√14 + 80

Question 3.
Multiply (√-1 +√-1) (a – b√-1)
Solution:
(√-1 +√-1) (a – b√-1)
= (i + i) (a – bi) = 2i(a – bi)
= 2ai – 2bi² = 2ai + 2b

Question 4.
Multiply (x – \(\frac{1+\sqrt{-3}}{2}\)) (x – \(\frac{1-\sqrt{3}}{2}\))
Solution:
(x – \(\frac{1+\sqrt{-3}}{2}\)) (x – \(\frac{1-\sqrt{3}}{2}\))
= (x + \(\frac{-1-i \sqrt{3}}{2}\)) (x + \(\frac{-1+i \sqrt{3}}{2}\))
= (x + ω) (x + ω²) = x² + ω²x + ωx + ω³
= x² + x (ω ² + ω) + 1 = x² –  x + 1

Question 5.
Express with rational denominator. \(\frac{1}{3-\sqrt{-2}}\)
Solution:
\(\begin{aligned}
& \frac{1}{3-\sqrt{-2}}=\frac{1}{3-\sqrt{2} \mathrm{i}}=\frac{3+\sqrt{2} \mathrm{i}}{(3-\sqrt{2} \mathrm{i})(3+\sqrt{2} \mathrm{i})} \\
& =\frac{3+\sqrt{2} \mathrm{i}}{9-2 \mathrm{i}^2}=\frac{3+\sqrt{2} \mathrm{i}}{9+2}=\frac{3+\mathrm{i} \sqrt{2}}{11}
\end{aligned}\)

Question 6.
\(\frac{3 \sqrt{-2}+2(-5)}{3 \sqrt{-2}-2 \sqrt{-2}}\)
Solution:

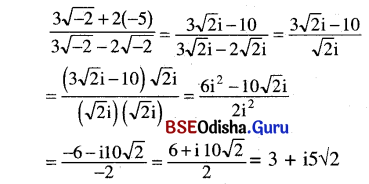
Question 7.
\(\frac{3+2 \sqrt{-1}}{2-5 \sqrt{-1}}+\frac{3-2 \sqrt{-1}}{2+5 \sqrt{-1}}\)
Solution:

Question 8.
\(\frac{a+x \sqrt{-1}}{a-x \sqrt{-1}}-\frac{a-x \sqrt{-1}}{a+x \sqrt{-1}}\)
Solution:

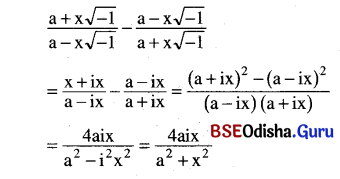
Question 9.
\(\frac{(x+\sqrt{-1})^2}{x-\sqrt{-1}}-\frac{\left(x-\sqrt{-1^2}\right)}{x+\sqrt{-1}}\)
Solution:

Question 10.
\(\frac{(a+\sqrt{-1})^3-(a-\sqrt{-1})^3}{(a+\sqrt{-1})^2-(a-\sqrt{-1})^2}\)
Solution:

Question 11.
Find the value of (- i)⁴ⁿ⁺³; when n is positive.
Solution:
(- i)⁴ⁿ⁺³
= (-i⁴ⁿ) (-i)³ = 1(- i³) = – (-i) = i

Question 12.
Find the square root of (a + 40i) + \(\sqrt{9-40 \sqrt{-i}}\)
Solution:

Question 13.
Express in the form of a + ib:
(i) \(\frac{3+5 i}{2-3 i}\)
Solution:

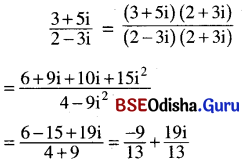
(ii) \(\frac{\sqrt{3}-i \sqrt{2}}{2 \sqrt{3}-i \sqrt{3}}\)
Solution

(iii) \(\frac{(\mathrm{I}+\mathrm{i})^2}{3-\mathrm{i}}\)
Solution:

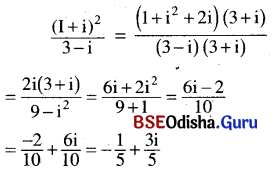
(iv) \(\frac{(a+i b)^3}{a-i b}-\frac{(a-i b)^3}{a+i b}\)
Solution:

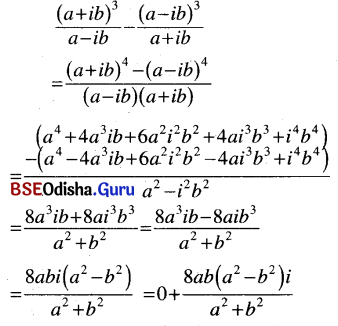
(v) \(\frac{1+i}{1-i}\)
Solution:
\(\frac{1+i}{1-i}\) = \(\frac{(1+i)^2}{2}=\frac{1-1+2 i}{2}\)
= i = 0 + i

Question 14.
Express the following points geometrically in the Argand plane.
(i) 1
Solution:
1 = 1 + i0 = (1, 0)

(ii) 3i
Solution:
3i = 0 + 3i = (0, 3)

(iii) – 2
Solution:
– 2 = – 2 + i0 = (- 2, 0)

(iv) 3 + 2i
Solution:
3 + 2i = (3, 2)

(v) – 3 + i
Solution:
– 3 + i = (- 3, 1)

(vi) 1-i
Solution:
1 – i = (1, – 1)

Question 15.
Show that the following numbers are equidistant from the origin:
√2 +i, 1 + i√2, i√3
Solution:
|√2 + i| = \(\sqrt{(\sqrt{2})^2+1^2}\) = √3
|1 + i√2| = \(\sqrt{1^2+(\sqrt{2})^2}\) = √3
and |i√3| = √3
∴ The points are equidistant from the origin.

Question 16.
Express each of the above complex numbers in the polar form.
Solution:

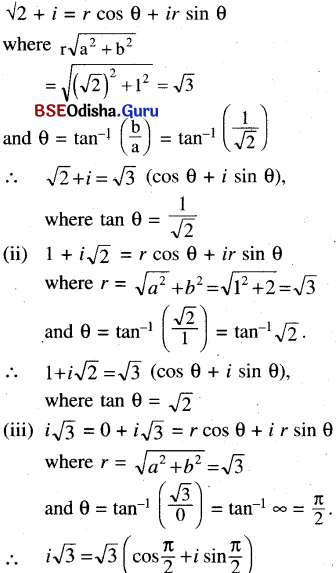
Question 17.
If 1, ω, ω² are the three cube roots of unity, prove that (1 + ω²)⁴ = ω
Solution:
L.H.S. = (1 + ω²)⁴ = (- ω)⁴ = ω⁴
= ω³ .ω = 1. ω = ω
= R.H.S. (Proved)

Question 18.
(1 – ω+ ω² ) (1 + ω – ω² ) = 4
Solution:
L.H.S. = (1 – ω+ ω² ) (1 + ω – ω² )
= (- ω – ω )(- ω² – ω² ) (∴ 1 + ω + ω² = 0)
= (- 2ω² – 2ω²) = 4ω³ = 4 = R.H.S.

Question 19.
(1 – ω) (1 – ω)² (1 – ω⁴) (1 – ω⁵) = 9
Solution:
L.H.S. =
(1 – ω) (1 – ω)² (1 – ω⁴) (1 – ω⁵)
= (1 – ω) (1 – ω²) (1 – ω) (1 – ω²)
= (1 – ω)² (1 – ω²)²
= {(1 – ω) (1 – ω²)}²
= (1 – ω² – ω + ω³)²
= {3 – (ω² + ω + 1)}²
= (3)² = 9 = R.H.S.

Question 20.
(2 + 5ω + 2ω² )⁶ = (2 + 2ω + 5ω² )⁶ =729
Solution:
L.H.S. = (2 + 5ω + 2ω² )⁶
(2 + 2ω² + 5ω)⁶ = {2(1 + ω² ) + 5ω}⁶
(- 2ω + 5ω)⁶ = (3ω)⁶ = 729ω⁶ = 729
Again, (2 + 2ω + 5ω² )⁶
= {2(1 + ω) + 5ω² )⁶
= (- 2ω² + 5ω² )⁶ = (3ω²)⁶
= 729ω¹² =729
∴ (2 + 5ω + 2ω² )⁶ = (2 + 2ω + 5ω² )⁶ =729

Question 21.
(1 – ω + ω² ) (1 – ω² + ω⁴) (1 – ω⁴ +ω²)  ….to 2n factors = 2²ⁿ
Solution:
L.H.S. = (1 – ω + ω² ) (1 – ω² + ω⁴) (1 – ω⁴ +ω²)  ….to 2n factors = 2²ⁿ
= (- ω – ω) (1 – ω² + ω) (1 – ω + ω² )  ….to 2n factors = 2²ⁿ
= (- 2ω) (- ω² – ω² ) (- ω – ω)  ….to 2n factors = 2²ⁿ
= [(- 2ω)(- 2ω) … to n factors] × [(- 2ω²)(- 2ω²) …. to n factors]
= (- 2ω)ⁿ × (- 2ω²)ⁿ = (4ω³)ⁿ = 4ⁿ = 2²ⁿ
R.H.S. (Proved)

Question 22.
Prove that x³ + y³ + z³– 3xyz
= (x + y + z) (x + ωy + ω²z) (x + yω² + zω)
Solution:
R.H.S. = (x + y + z) (x + ωy + ω²z) (x + yω² + zω)
= (x + y + z) (x + xyω² + zxω + xyω + y²ω³+ yz ω2 + zxω² + yzω⁴ + z²ω³)
= (x + y + z) [x² + y² + z² + xy (ω² + ω) +yz (ω² + ω) + zx(ω² + ω)]
= (x + y + z) (x² + y² + z² – xy – yz – zx)
= x³ + y³ + z³ – 3xyz = L.H.S. (Proved)

Question 23.
If x = a + b, y = aω + b ω², z = aω² + bω show that
(1) xyz = a³ + b³
Solution:
L.H.S. = xyz
= (a + b) (a ω + b ω²) (a ω² + b ω)
= (a + b) (a² ω³ + ab ω² + ab ω⁴ + b² ω³)
= (a + b) {a² + b² + ab(ω² + ω)}
= (a + b) (a² – ab + b²) = a³ + b³ = R.H.S. (Proved)

(2) x² + y² + z² = 6ab
Solution:
L.H.S. = x² + y² + z²
= (a + b)² + (a ω + b ω²)² (a ω² + b ω)²
= a² + b² + 2ab + a² ω² + b² ω⁴ + 2ab ω³ + a² ω⁴ + b² ω² + 2ab ω³
= a² + a² ω² + a² ω + b² + b² ω + b² ω² + 2ab + 2ab + 2ab
= a²(1 + ω² + ω) + b² (1 + ω + ω²) + 6ab
= 0 + 0 + 6ab = 6ab = R.H.S. (Proved)

(3) x³ + y³ + z³ = 3(a³ + b³)
Solution:
L.H.S. = x³ + y³ + z³
= (a + b)³ + (a ω + b ω²)³ + (aω² + b²)³
= a³ + 3a²b + 3ab² + b³ + a³ ω³ + 3a²b² bω² + 3a ωb² ω⁴ + b³ ω⁶ + a³ ω⁶ + 3a² ω⁴bω + 3a ω²b² ω² + b³ ω³
= a³ + a³ + a³ + b³ + b³ + b³ + 3a²b(1 + ω⁴ + ω⁵) + 3ab² (1 + ω⁵ + ω⁴)
= 3a³ + 3b³ + 0 + 0 = 3 (a³ + b³) = R.H.S. (Proved)

Question 24.
If ax + by + cz = X, cx + by + az = Y, bx + ay + cz = Z
show that (a² + b² + c² – ab – bc- ca) (x² +y² + z² – xy – yz – zx) = X² + Y² + Z² – YZ – ZX – XY
Solution:
L.H.S.
= (a² + b² + c² – ab – bc – ca) (x² + y² + z² – xy – yz – zx)
= (a + b ω + cω²) (a + bω² + cω) (x + yω + zω)² (x + yω² + z ω) (Refer Q.No.22)
= {(a + bω + cω²) (x + yω + zω²)} {(a + bω² + cω) (x + yω² + zω)}
= (ax + ayω + azω² + bx ω + byω² + bzω³ + cxω² + cyω³ + czω⁴) × (ax + ay ω² + azω + bxω² + byω⁴ + bzω³ + cxω + cyω³ + czω²)
= {(ax + cy + bz) + (cx + by + az) ω + (bx + ay + cz) ω²} x (ax + cy + bz) + (cx + by + az) ω + (bx + ay + cz) ω²}
= (X + Yω² + Zω) (X + Yω + Zω²)
= X² + Y² + Z² – XY – YZ – ZX (Refer Q. No. 22)
(Where X = ax + cy + bz.
Y = cx + by + az.
Z = bx + ay + cz).