Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 7 Linear Inequalities Ex 7(a) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 7 Linear Inequalities Exercise 7(a)
Question 1.
Determine whether the solution set is finite or infinite or empty:
(i) x < 1000, x ∈ N
Solution:
Finite
(ii) x < 1, x ∈ Z (set of integers)
Solution:
Infinite
(iii) x < 2, x is a positive integer.
Solution:
Finite
(iv) x < 1, x is a positive integer.
Solution:
Empty
![]()
Question 2.
Solve as directed:
(i) 5x ≤ 20 in positive integers, in integers.
Solution:
5x ≤ 20
⇒ \(\frac{5 x}{5} \leq \frac{20}{5}\)
⇒ x ≤ 4
If x is a positive integer, then the solution set is {1, 2, 3, 4}
If x is an integer, then the solution set is:
S = {x : x ∈ Z and x ≤ 4}
= { ….. -3, -2, -1, 0, 1, 2, 3, 4}
(ii) 2x + 3 > 15 in integers, in natural numbers.
Do you mark any difference in the solution sets?
Solution:
2x + 3 > 15
⇒ 2x + 3 – 3 > 15 – 3
⇒ 2x > 12
⇒ \(\frac{2 x}{2}>\frac{12}{2}\)
⇒ x > 6
If x ∈ Z, then the solution set is S = (x : x ∈ Z and x > 6}
= {7, 8, 9…… }
If x ∈ N. then the solution set is S = {x : x ∈ N and x > 6}
= {7, 8, 9…… }
Two solution sets are the same.
(iii) 5x + 7 < 32 in integers, in non-negative integers.
Solution:
5x + 7 < 32
⇒ 5x + 7 – 7 < 32 – 7
⇒ 5x < 25
⇒ \(\frac{5 x}{5}<\frac{25}{5}\)
⇒ x < 5
If x ∈ Z, then the solution set is S = { x : x ∈ Z and x < 5 }
= {…..-3, -2, -1, 0, 1, 2, 3, 4}
If x is a non-negative solution then the solution set is S = {x : x is a non-negative integer < 5}
= (0, 1,2, 3,4}
(iv) -3x – 8 > 19, in integers, in real numbers.
Solution:
– 3x – 8 > 19
⇒ – 3 x – 8 + 8 > 19 + 8
⇒ – 3x > 27
⇒ \(\frac{-3 x}{-3}<\frac{27}{-3}\)
⇒ x < – 9
If x ∈ Z, then the solution set is S = (x : x ∈ Z and x < – 9}
= { ……..- 11, – 10}
If x ∈ R then the solution set is S = {x : x ∈ R and x < – 9}
= (∞, – 9)
(v) |x – 3| < 11, in N and in R.
Solution:
|x – 3| < 11
⇒ – 1 < x – 3 < 11
⇒ – 11 + 3 < x – 3 + 3 < 11+3
⇒ – 8 < x < 14
If x ∈ N the solution set is S = {1, 2, 3, 4, 5……..12, 13}
If x ∈ R then the solution set is: S = {x : x ∈ R and – 8 < x < 14}
= (- 8, 14)
Question 3.
Solve as directed:
(i) 2x + 3 > x – 7 in R
Solution:
2x + 3 > x – 7
⇒ 2x – x > – 7 – 3
⇒ x > – 10
x ∈ R, the solution set is S = (x : x ∈ R and x > – 10} = (-10, ∞)
(ii) \(\frac{x}{2}+\frac{7}{3}\) < 3x – 1 in R
Solution:
\(\frac{x}{2}+\frac{7}{3}\) < 3x – 1
\(\frac{3 x+14}{6}\) < 3x – 1
⇒ 3x + 14 < 18x – 6
⇒ 3x – 18x < – 6 – 14
⇒ – 15x < – 20
⇒ \(\frac{-15 x}{-15}>\frac{-20}{-15}\)
⇒ x > \(\frac{4}{3}\)
If x ∈ R, the solution set is S = \(\left(\frac{4}{3}, \infty\right)=\left\{x: x \in R \text { and } x>\frac{4}{3}\right\}\)
(iii) \(\frac{x}{2}-\frac{x}{3}+\frac{x}{5} \leq \frac{11}{3}\) for non-negative real numbers.
Solution:
\(\frac{x}{2}-\frac{x}{3}+\frac{x}{5} \leq \frac{11}{3}\)
⇒ \(\frac{15 x-10 x+6 x}{30}\) ≤ \(\frac{11}{3}\)
⇒ 11x ≤ \(\frac{11}{3}\) × 30
⇒ 11x ≤ 110
⇒ x ≤ 10
If x is a non-negative real number then the solution set is S = {x : x ∈ R and 0 ≤ x ≤ 10}
= {0, 10}
(iv) 2(3x – 1) < 7x + 1 < 3 (2x + 1) for real values.
Solution:
2(3x – 1) < 7x + 1 < 3(2x + 1)
⇒ 6x – 2 < 7x + 1< 6x + 3
⇒ – 2 < x + 1 < 3
⇒ – 3 < x < 2
If x ∈ R, the solution set is S = (x : x ∈ R and -3 < x < 2}
= {-3, 2}
(v) 7(x – 3) ≤ 4 (x + 6), for non-negative integral values.
Solution:
7(x – 3) ≤ 4(x + 6)
⇒ 7x – 21 ≤ 4x + 24
⇒ 7x – 4x ≤ 24 + 21
⇒ 3x ≤ 45
⇒ x ≤ 9
If x is a non-negative integer the solution set is S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
(vi) Convert to linear inequality and solve for natural numbers: (x – 2) (x – 3) < (x + 3) (x – 1)
Solution:
(x – 2) (x – 3) < (x + 3) (x – 1)
⇒ x2 – 5x + 6 < x2 + 2x – 3
⇒ – 5x + 6 < 2x – 3
⇒ – 5x – 2x < – 3 – 6
⇒ – 7x < – 9
⇒ x > \(\frac{9}{7}\)
If x ∈ N, the solution set is S = {2, 3, 4 }
(vii) Solve in R, \(\frac{x}{2}\) + 1 ≤ 2x – 5 < x. Also, find its solution in N.
Solution:
\(\frac{x}{2}\) + 1 ≤ 2x – 5 < x
⇒ \(\frac{x}{2}\) +1 ≤ 2x – 5 and 2x – 5 < x
⇒ \(\frac{x}{2}\) – 2x ≤ – 5 – 1 and x < 5
⇒ \(\frac{-3x}{2}\) ≤ – 6 and x < 5
⇒ – 3x ≤ – 12 and x < 5
⇒ x ≥ 4 and x < 5
⇒ 4 ≤ x < 5
If x ∈ R, the solution set is S = {x : x ∈ R and 4 < x < 5}
= {4, 5}
If x ∈ N, the solution set is S = { 4 }
(viii) Solve in R and also in Z: \(\frac{3 x+1}{5} \geq \frac{x+2}{3}-\frac{5-3 x}{5}\)
Solution:
\(\frac{3 x+1}{5} \geq \frac{x+2}{3}-\frac{5-3 x}{5}\)
⇒ \(\frac{3 x+1}{5} \geq \frac{5 x+10-15+9 x}{15}\)
⇒ 3x + 1 ≥ \(\frac{14 x-5}{3}\)
⇒ 9x + 3 ≥ 14x – 5
⇒ 9x – 14x ≥ – 5 – 3
⇒ – 5x ≥ – 8
⇒ x ≤ \(\frac{8}{5}\)
If x ∈ R, then the solution set is S = (x : x ∈ R and x ≤ \(\frac{8}{5}\)}
= (- ∞, \(\frac{8}{5}\))
If x ∈ Z, then the solution set is S = { x : x ∈ Z and x ≤ \(\frac{8}{5}\)}
= {……. -3, -2, -1, 0, 1}
![]()
Question 4.
Solve |x – 1| >1 and represent the solution on the number line.
[Exhaustive hints: By definition of modulus function
For x – 1 ≥ 0 or x ≥ 1, |x – 1| > 1
⇔ x – 1 > 1 ⇔ x > 2 ⇔ x ∈ (2, ∞)
For x- 1 < 0 or x < 1, |x – 1| > 1
⇔ – (x – 1) > 1
⇔ x – 1 < -1 (multiplication by -1 reverses the inequality)
⇔ x < 0 ⇔ x ∈ ( -∞, 0)
∴ The solution set is the Union,
(-∞, 0) ∪ (2, ∞) Show this as two disjoint open intervals on the number line, i.e., real line.]
Solution:
|x – 1| > 1
⇒ – 1 > x – 1 > 1
⇒ 0 > x > 2
⇒ x < 0 and x > 2
∴ The solution set is S = {x : x ∈ R, x < 0 and x > 2}
= (-∞, 0) ∪ (2, ∞)
We can show this solution in the number line as

Question 5.
Solve in R and represent the solution on the number line.
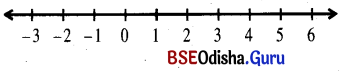
(i) |x – 5| < 1
Solution:
|x – 5| < 1
⇒ – 1< x – 5 < 1
⇒ 4 < x < 6
If x ∈ R, then the solution set is S = (4, 6)
We can represent the solution on the number line as
(ii) \(\frac{x}{5}<\frac{2 x+1}{3}+\frac{1-3 x}{6}\)
Solution:
\(\frac{x}{5}<\frac{2 x+1}{3}+\frac{1-3 x}{6}\)
⇒ \(\frac{x}{5}<\frac{4 x+2+1-3 x}{6}\)
⇒ \(\frac{x}{5}<\frac{x+3}{6}\)
⇒ 6x < 5x + 15
⇒ x < 15
If x ∈ R, the solution set is S = (-∞, 5)
We can represent the solution on the number line as
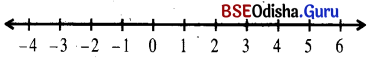
(iii) 2x + 1 ≥ 0
Solution:
2x + 1 ≥ 0
⇒ 2x ≥ -1
⇒ x ≥ -1/2
If x ∈ R, then the solution set is S = [\(-\frac{1}{2}\), ∞]
We can represent the solution on the number line as
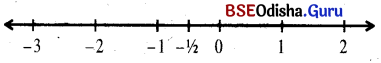
(iv) \(\frac{x-1}{2} \leq \frac{x+1}{3}<\frac{3 x-1}{6}\)
Solution:
\(\frac{x-1}{2} \leq \frac{x+1}{3}<\frac{3 x-1}{6}\)
⇒ 3x – 3 ≤ 2x + 2 < 3x – 1
⇒ 3x – 3 ≤ 2x + 2 and 2x + 2 < 3x – 1
⇒ x ≤ 5 and – x < – 3
⇒ x ≤ 5 and x > 3
⇒ 3 < x ≤ 5
If x ∈ R, the solution set is S = {3, 5}
We can represent the solution on the number line as

Question 6.
In a triangle, ABC; AB, BC, and CA are x, 3x + 2, and x + 4 units respectively where x ∈ N. Find the length of its sides. (Hint: Apply triangle-inequality).
Solution:
Given AB = x
BC = 3x + 2
and CA = x + 4
Now AB + AC > BC (Triangle inequality)
⇒ x + x + 4 > 3x + 2
⇒ 2x + 4 > 3x + 2
⇒ – x > – 2
⇒ x < 2
As x ∈ N we have x = 1
The sides of triangle ABC are
AB = 1 unit
BC = 5 units
and CA = 5 units
![]()
Question 7.
The length of one side of a parallelogram is 1 cm. shorter than that of its adjacent side. If its perimeter is at least 26 c.m., find the minimum possible lengths of its sides.
Solution:
Let the longer side = x cm
∴ The smaller side = (x – 1) cm
Perimeter = 2(x + (x – 1)) = 4x – 2 cm
According to the question
4x – 2 ≥ 26
⇒ 4x ≥ 28
⇒ x > 7
The minimum value of x = 7.
∴ The minimum length of the sides is 7cm and 6 cm.
Question 8.
The length of the largest side of a quadrilateral is three times that of its smallest side. Out of the other two sides, the length of one is twice that of the smallest and the other is 1 cm. longer than the smallest. If the perimeter of the quadrilateral is at most 36 c.m., then find the maximum possible lengths of its sides.
Solution:
Let the smallest side = x cm.
Largest side = 3 times x = 3x cm.
The other two sides are 2x cm and x + 1 cm.
⇒ The perimeter = x + 3x + 2x + x + 1
= 7x + 1 cm
According to the question:
7x + 1 ≤ 36
⇒ 7x ≤ 35
⇒ x ≤ 5
Maximum value of x = 5
∴ The maximum possible length of sides are x = 5 cm, 3x = 15 cm, 2x = 10 cm, and x + 1 = 6 cm.
Question 9.
Find all pairs of consecutive odd numbers each greater than 20, such that their sum is less than 60.
Solution:
Let two consecutive odd numbers are
2n – 1 and 2n + 1
Now 2n – 1 > 20 and 2n + 1 > 20
But their sum = 2n – 1 + 2n + 1
= 4n < 60
⇒ n < 15
for n = 14 two numbers are 27, 29
for n = 13 two numbers are 25, 27
for n = 12 two numbers are 23, 25
for n = 11 two numbers are 21, 23
∴ All pairs are 21, 23; 23, 25; 25, 27 and 27, 29
Question 10.
Find all pairs of even numbers each less than 35, such that their sum is at least 50.
Solution:
Let two even numbers be x and y.
According to the question
x < 35, y < 35 and x + y ≥ 50
⇒ x ≤ 34, y ≤ 34 and x + y ≥ 50
⇒ x + y ≤ 70, x + y ≥ 50
⇒ 50 ≤ x + y ≤ 70
If x + y = 50 the numbers are {34, 16}, {32, 18}, {30, 20}, {28, 22}, {26, 24}
If x + y = 52 the numbers are {34, 18}, {32, 20}, {30, 22}, {28, 24}, {26, 26}
If x + y = 34 the numbers are {34, 20}, {32, 22}, {30, 24}
If x + y = 56 the numbers are {34, 22}, {32, 24}, {30, 26}, {28, 28}
If x + y = 58 the numbers are {34, 24}, {32, 26}, {30, 28}
If x + y = 60 the numbers are {34, 26}, {32, 28}, {30, 30}
If x + y = 62 the numbers are {34, 28}, {32, 30}
If x + y = 64 the numbers are {34, 30}, {32, 32}
If x + y = 68 the numbers are {34, 34}
