Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 7 ପରିବ୍ୟୟ Long Answer Questions.
CHSE Odisha 12th Class Economics Chapter 7 Long Answer Questions in Odia Medium
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
1. ଉତ୍ପାଦନ ପରିବ୍ୟୟ କହିଲେ କ’ଣ ବୁଝାଏ ? ସ୍ଵଳ୍ପକାଳୀନ ମୋଟ ପରିବ୍ୟୟର ଉପାଦାନଗୁଡ଼ିକ ବର୍ଣନା କରି ମୋଟ ପରିବ୍ୟୟ କିପରି ନିର୍ଦ୍ଧାରଣ କରାଯାଏ ରେଖାଚିତ୍ର ସାହାଯ୍ୟରେ ବୁଝାଅ । କିମ୍ବା, ଉତ୍ପାଦନ ପରିବ୍ୟୟ କାହାକୁ କୁହାଯାଏ ? ସ୍ଥିର ପରିବ୍ୟୟ ଓ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ଏହା କିପରି ସ୍ଵଳ୍ପକାଳରେ ମୋଟ ପରିବ୍ୟୟ ନିର୍ଣ୍ଣୟ କରିଥାଏ ବର୍ଣ୍ଣନା କର ।
Answer:
ପରିବ୍ୟୟ – ଅର୍ଥଶାସ୍ତ୍ରରେ ପରିବ୍ୟୟ ଅଭିଧାରଣା ଏକ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ଧାରଣାଭାବେ ସୁସ୍ପଷ୍ଟ । ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ‘ପରିବ୍ୟୟ’ ଶବ୍ଦର ଗୁରୁତ୍ଵ ଓ ବ୍ୟାପକତା ଭରିରହିଛି । ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଉତ୍ପାଦନକର୍ତ୍ତା ଉତ୍ପାଦନର ଉପାଦାନ; ଯଥା- ଭୂମି, ଶ୍ରମ ଓ ପୁଞ୍ଜି ସହାୟତାରେ ଦ୍ରବ୍ୟ ସାମଗ୍ରୀ ଉତ୍ପାଦନ କରିଥା’ନ୍ତି ।
ଅର୍ଥାତ୍ ଭୂମି, ଶ୍ରମ ଓ ପୁଞ୍ଜି ଆଦିର ଭୂମିକା ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ସ୍ପଷ୍ଟଭାବରେ ଅନୁଭବ କରିହୁଏ । ଏହି ଉପାଦାନମାନଙ୍କର ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ନିଜସ୍ଵ ଅବଦାନ ପାଇଁ ଏହାର ବ୍ୟୟଭାର ବହନ କରିଥା’ନ୍ତି । ତେଣୁ ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଉତ୍ପାଦନକର୍ତ୍ତା ଉପାଦାନମାନଙ୍କର ନିୟୋଜନ ଯୋଗୁଁ ଯେଉଁ ବ୍ୟୟ ସାଧନ କରିଥା’ନ୍ତି, ତାହାକୁ ଅର୍ଥଶାସ୍ତ୍ରରେ ‘ଉତ୍ପାଦନର ପରିବ୍ୟୟ’ କୁହାଯାଏ ।
ଉତ୍ପାଦନ ପରିବ୍ୟୟକୁ ବିଭିନ୍ନଭାବରେ ବ୍ୟାଖ୍ୟା କରାଯାଇଥାଏ । ଅର୍ଥାତ୍ ଉତ୍ପାଦନ ପରିବ୍ୟୟକୁ ବିଭିନ୍ନଭାବରେ ପରିପ୍ରକାଶ କରାଯାଇଥାଏ; ଯଥା- ମୁଦ୍ରାଗତ ପରିବ୍ୟୟ ଓ ବାସ୍ତବ ପରିବ୍ୟୟ; ସୁବ୍ୟକ୍ତ ପରିବ୍ୟୟ ଓ ଅବ୍ୟକ୍ତ ପରିବ୍ୟୟ, ବିକଳ୍ପ ବା ସୁଯୋଗ ପରିବ୍ୟୟ ଇତ୍ୟାଦି । ମାତ୍ର ସମସ୍ତ ପ୍ରକାରର ପରିବ୍ୟୟ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଆଭିମୁଖ୍ୟ ଉପରେ ପର୍ଯ୍ୟବସିତ, ତାହାହେଲା ଦ୍ରବ୍ୟ ଉତ୍ପାଦନ । ତେଣୁ ପରିବ୍ୟୟକୁ ସର୍ବସମ୍ମତଭାବେ ଉତ୍ପାଦନଜନିତ ବ୍ୟୟ ବୋଲି ବିବେଚନା କରାଯାଇଥାଏ ।
ମୋଟ ପରିବ୍ୟୟ – ସରଳ ଭାଷାରେ, କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣର ଦ୍ରବ୍ୟ ଉତ୍ପାଦନ ପାଇଁ ସାମଗ୍ରିକଭାବେ ଯେଉଁ ବ୍ୟୟ ଉତ୍ପାଦନର ଉପାଦାନମାନଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ କରାଯାଏ ତାହାକୁ ମୋଟ ପରିବ୍ୟୟ କୁହାଯାଏ । ଅନ୍ୟ ଅର୍ଥରେ ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ସାମଗ୍ରିକଭାବେ ସମସ୍ତ ମୌଦ୍ରିକ ପରିବ୍ୟୟର ସମଷ୍ଟିକୁ ମୋଟ ପରିବ୍ୟୟ କୁହାଯାଏ । ଅଧ୍ୟାପକ ଡୋଲେଙ୍କ ଭାଷାରେ, ‘‘ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣର ଦ୍ରବ୍ୟ ଉତ୍ପାଦନ ନିମନ୍ତେ କରାଯାଉଥିବା ସମସ୍ତ ପ୍ରକାର ବ୍ୟୟର ସମଷ୍ଟିକୁ ମୋଟ ପରିବ୍ୟୟ କୁହାଯାଏ ।’’
ମୋଟ ପରିବ୍ୟୟର ସ୍ଵଳ୍ପକାଳୀନ ବିଶ୍ଳେଷଣ – ମୋଟ ପରିବ୍ୟୟର ବିଶ୍ଳେଷଣ ସାଧାରଣତଃ ସମୟ ଭିଭିରେ କରାଯାଇଥାଏ । ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ସମୟ ଉପାଦାନର ଗୁରୁତ୍ବ ରହିଥିବାରୁ ଏହି ସମୟ ଉପାଦାନକୁ ସ୍ଵଳ୍ପକାଳ ଓ ଦୀର୍ଘକାଳ ଆଖ୍ୟା ଦିଆଯାଇଥାଏ । ଯେଉଁ ସମୟ ମଧ୍ୟରେ ପ୍ରତିଷ୍ଠାନର ଆୟତନରେ କୌଣସି ପରିବର୍ତ୍ତନ କରିବା ସମ୍ଭବପର ନୁହେଁ ତାହାକୁ ସ୍ଵଳ୍ପକାଳ କୁହାଯାଏ । ସ୍ବକାଳରେ ସମସ୍ତ ଉପାଦାନ ପରିବର୍ତ୍ତନଶୀଳ ନୁହନ୍ତି; କେତେକ ଉପାଦାନ ସ୍ଥିର ରହି କେତେକ ଉପାଦାନ ପରିବର୍ତ୍ତିତ ହୋଇଥା’ନ୍ତି । ମାତ୍ର ଦୀର୍ଘକାଳରେ ସମସ୍ତ ଉପାଦାନ ପରିବର୍ତ୍ତନଶୀଳ ହୋଇଥା’ନ୍ତି ।
![]()
ତେଣୁ ସ୍ଵଳ୍ପକାଳରେ ପରିବ୍ୟୟକୁ ଦୁଇଟି ସ୍ଵତନ୍ତ୍ର ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଥାଏ; ଯଥା- ସ୍ଥିର ପରିବ୍ୟୟ (Fixed cost) ଓ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (Variable cost)
ସ୍ଥିର ପରିବ୍ୟୟ – ସ୍ଵଳ୍ପକାଳରେ ସ୍ଥିର ରହୁଥିବା ଉପାଦାନମାନଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ ଯେଉଁ ବ୍ୟୟ କରାଯାଏ, ତାହାକୁ ସ୍ଥିର ପରିବ୍ୟୟ କୁହାଯାଏ । ଏହି ସ୍ବତନ୍ତ୍ର ସ୍ଵଳ୍ପକାଳୀନ ପରିବ୍ୟୟ ଉତ୍ପାଦର ପରିମାଣ ପରିବର୍ତନ ସହ ପରିବର୍ତ୍ତିତ ହୋଇନଥାଏ । ଉତ୍ପାଦନର ପରିମାଣ ନିର୍ବିଶେଷରେ ଏହି ସ୍ଥିର ପରିବ୍ୟୟ ଅପରିବର୍ତିତ ରହିଥାଏ । ସ୍ଥିର ପରିବ୍ୟୟକୁ ଅତିରିକ୍ତ ପରିବ୍ୟୟ (Supplementary cost) କିମ୍ବା ଉପରି ପରିବ୍ୟୟ (Overhead cost) କୁହାଯାଏ । ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟର ସମସ୍ତ ଏକକ ପାଇଁ ଏହି ସ୍ଥିର ପରିବ୍ୟୟ ସମାନ ରହିଥାଏ ।
ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ – ସ୍ଵଳ୍ପକାଳରେ ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଯେଉଁ ପରିବ୍ୟୟ ଉତ୍ପାଦନ ପରିମାଣର ବୃଦ୍ଧି ବା ହ୍ରାସ ସହ ବୃଦ୍ଧି ବା ହ୍ରାସ ହୋଇଥାଏ, ତାହାକୁ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ କୁହାଯାଏ । ଅର୍ଥାତ୍ ଉତ୍ପାଦର ପରିବର୍ତ୍ତନ ସହ ଏହା ପରିବର୍ତ୍ତିତ ହୋଇଥାଏ । ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟକୁ ପ୍ରତ୍ୟକ୍ଷ ପରିବ୍ୟୟ ( Direct cost) ବା ପ୍ରଧାନ ପରିବ୍ୟୟ (Prime cost) କୁହାଯାଏ ।
ଉପରୋକ୍ତ ବିଶ୍ଳେଷଣରୁ ପ୍ରତିଫଳିତ ହୁଏ ଯେ, ସ୍ଵଳ୍ପକାଳରେ ମୋଟ ପରିବ୍ୟୟର ଦୁଇଟି ଉପାଦାନ ବା ଉପାଂଶ ରହିଛି । ତାହା ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ଓ ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ । ତେଣୁ ମୋଟ ପରିବ୍ୟୟ ହେଉଛି ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ଓ = ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ + ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ।
ମୋଟ ପରିବ୍ୟୟ, ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ଓ ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟର ସମ୍ମିଶ୍ରଣ ଅଟେ । ଉତ୍ପାଦନର ମୋଟ ପରିବ୍ୟୟ ଉତ୍ପାଦର ସ୍ତର ଉପରେ ନିର୍ଭର କରେ । ଉତ୍ପାଦନ ପରିମାଣର ବୃଦ୍ଧି ସହ ମୋଟ ପରିବ୍ୟୟ ବୃଦ୍ଧି ପାଏ ଓ ହ୍ରାସ ସହ ମୋଟ ପରିବ୍ୟୟ ହ୍ରାସ ପାଏ । କିନ୍ତୁ ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ଅପରିବର୍ତିତ ରହୁଥିବାରୁ କେବଳ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ଯୋଗୁ ହିଁ ମୋଟ ପରିବ୍ୟୟରେ ପରିବର୍ତ୍ତନ ଘଟିଥାଏ । ତେଣୁ ସ୍ୱଳ୍ପକାଳରେ ପରିବ୍ୟୟର ବୃଦ୍ଧି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟର ବୃଦ୍ଧି ଯୋଗୁଁ ଘଟିଥାଏ ।
ମୋଟ ପରିବ୍ୟୟ, ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ଓ ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କକୁ ନିମ୍ନଲିଖ୍ ଗାଣିତିକ ବିଶ୍ଳେଷଣ ଓ ରୈଖ୍ୟକ ଉପସ୍ଥାପନାଦ୍ଵାରା ପ୍ରଦର୍ଶିତ କରାଯାଇପାରେ ।
| ଉତ୍ପାଦର ଏକକ | ମୋଟ ସ୍ଥିର ପରିବ୍ଯୟ (ଟଙ୍କା) | ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ଯୟ (ଟଙ୍କା) | ମୋଟ ପରିବ୍ଯୟ (ମୋଟ ସ୍ଥିର ପରିବ୍ଯୟ
+ ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ଯୟ) |
| 0 | 10 | 0 | 10 |
| 1 | 10 | 10 | 20 |
| 2 | 10 | 18 | 28 |
| 3 | 10 | 25 | 35 |
| 4 | 10 | 31 | 41 |
| 5 | 10 | 36 | 46 |
| 6 | 10 | 40 | 50 |
| 7 | 10 | 60 | 70 |
| 8 | 10 | 90 | 100 |
ଉପରୋକ୍ତ ସାରଣୀରୁ ପ୍ରତୀୟମାନ ହୁଏ ଯେ, ମୋଟ ସ୍ଥିର ଉପାଦାନ ଉତ୍ପାଦନର ଯେକୌଣସି ପରିମାଣ ପାଇଁ ସ୍ଥିର (10 ଟଙ୍କା) ରହିଛି । ଏପରିକି ଉତ୍ପାଦର ପରିମାଣ ‘ଶୂନ୍ୟ’ ହେଲେ ମଧ୍ୟ ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ସେହି 10 ଟଙ୍କା ରହିଛି । ଦ୍ବିତୀୟତଃ, ଉତ୍ପାଦନ ପରିମାଣର ବୃଦ୍ଧି ସହ ପରିବର୍ଭନୀୟ ପରିବ୍ୟୟର ପରିମାଣ ବୃଦ୍ଧି ପାଇଛି । ଉତ୍ପାଦନର ପରିମାଣ ‘ଶୂନ୍ୟ’ବେଳେ ମୋଟ ପରିବର୍ତ୍ତନୀୟ ମଧ୍ଯ ‘ଶୂନ୍ୟ’ ରହିଛି । କ୍ରମଶଃ ମୋଟ ଉତ୍ପାଦର ପରିମାଣ ବୃଦ୍ଧି ସହ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟର ସମଷ୍ଟି (ଚତୁର୍ଥ ସ୍ତମ୍ଭ) ଏବଂ ଏହି ପରିବ୍ୟୟର ବୃଦ୍ଧି କେବଳ ପରିବର୍ତ୍ତନୀୟ ଉପାଦାନର ବୃଦ୍ଧି ଯୋଗୁଁ ଘଟିଥାଏ । ନିମ୍ନସ୍ଥ ଚିତ୍ରରେ OX- ଅକ୍ଷ ଉତ୍ପାଦର ପରିମାଣ ଓ OY- ଅକ୍ଷ ପରିବ୍ୟୟର ପରିମାଣକୁ ପ୍ରତିଫଳିତ କରୁଅଛି ।
ରୈଖ୍ୟକ ଉପସ୍ଥାପନା – ନିମ୍ନସ୍ଥ ଚିତ୍ରରେ OX- ଅକ୍ଷ ଉତ୍ପାଦର ପରିମାଣ ଓ OY- ଅକ୍ଷ ପରିବ୍ୟୟର ପରିମାଣକୁ ପ୍ରତିଫଳିତ କରୁଅଛି ।
FW ସରଳରେଖାଟି ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ସୂଚିତ କରୁଛି । ଏହି ରେଖାଟି OX ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇଥିବାରୁ ଉତ୍ପାଦର ଯେକୌଣସି ପରିବର୍ତ୍ତନ ଏହି ପରିବ୍ୟୟ ଉପରେ କୌଣସି ପ୍ରଭାବ ପକାଇ ପାରୁନାହିଁ । ଅର୍ଥାତ୍ ଯେକୌଣସି ପରିମାଣର ଉତ୍ପାଦ କ୍ଷେତ୍ରରେ ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ଅପରିବର୍ତ୍ତିତ ରହିଛି । ଏପରିକି ମୋଟ ଉତ୍ପାଦ ‘ଶୂନ୍ୟ’ ହେଲେ ମଧ୍ୟ ଉତ୍ପାଦନକର୍ତ୍ତା OF ପରିମାଣର ସ୍ଥିର ପରିବ୍ୟୟ ବହନ କରୁଛନ୍ତି । ସେହିପରି OM, ON ଓ OQ ପରିମାଣର ଉତ୍ପାଦ ପାଇଁ ସେହି ଏକା ପରିମାଣର ସ୍ଥିର ପରିବ୍ୟୟ (OF) ବ୍ୟୟ କରାଯାଇଛି ।
ମୋଟ ପରିବ୍ୟୟର ଦ୍ବିତୀୟ ଉପାଂଶ (ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ)ଟି OV ରେଖାଦ୍ଵାରା ସୂଚିତ ହୋଇଛି । ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ଉତ୍ପାଦ ପରିମାଣର ବୃଦ୍ଧି ସହ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହୋଇଛି । ଉତ୍ପାଦର ପରିମାଣ ଶୂନ୍ୟ ଥିବାବେଳେ ମୋଟ ପରିବର୍ଭନୀୟ ପରିବ୍ୟୟ ମଧ୍ୟ ଶୂନ୍ୟ ହୋଇଛି (OV ଚକ୍ରରୁ ପ୍ରମାଣିତ) । ସେହିପରି OM, ON, OQ ପରିମାଣର ଉତ୍ପାଦ ପାଇଁ ଯଥାକ୍ରମେ MA, NB ଓ QC ପରିମାଣର ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ଖର୍ଚ୍ଚ ହୋଇଛି ।
ଏଠାରେ OQ > ON > OM
QC > NB > MA
![]()
ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ସମାନ ହାରରେ ବୃଦ୍ଧି ପାଏ ନାହିଁ । କାରଣ ସ୍ଵଳ୍ପକାଳରେ ଉତ୍ପାଦନ କ୍ରମହ୍ରାସମାନ ଉତ୍ପନ୍ନ ସୂତ୍ରର ବଶବର୍ତୀ ହୋଇଥାଏ । ଫଳରେ ଏହି ସୂତ୍ରର ତିନୋଟି ପର୍ଯ୍ୟାୟରେ ଯଥାକ୍ରମେ ବର୍ଦ୍ଧିଷ୍ଣୁ ଉତ୍ପନ୍ନ ସୂତ୍ର, ସମାନୁପାତିକ ଉତ୍ପନ୍ନ ସୂତ୍ର ଓ କ୍ରମହ୍ରାସମାନ ଉତ୍ପନ୍ନ ସୂତ୍ରରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଥାଏ । ଏହି କାରଣରୁ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ରେଖାର
ଏହି ସ୍ବତନ୍ତ୍ର ଆକୃତି ହୋଇଥାଏ (OV ରେଖା) । ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟର ବୃଦ୍ଧିର ହାର ପ୍ରଥମେ ମନ୍ଥର ହୋଇଥିବାବେଳେ ପରବର୍ତ୍ତୀ ସ୍ତରରେ ତୀଖ ହୋଇଥାଏ ।
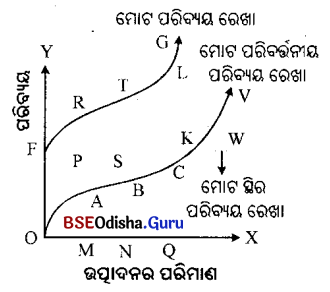
ଚିତ୍ରରେ ମୋଟ ପରିବ୍ୟୟ ରେଖା FG ଦ୍ଵାରା ଚିହ୍ନିତ ହୋଇଛି । ଏହି ରେଖାଟି ସ୍ଥିର ପରିବ୍ୟୟ ରେଖା ଓ ପରିବର୍ତ୍ତନୀୟ = ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ + ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ । ତେଣୁ ଉତ୍ପାଦର ବିଭିନ୍ନ ସ୍ତରରେ ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ଓ ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ମଧ୍ୟରେ ଥିବା ଉଲମ୍ବ ଦୂରତ୍ବକୁ ଯୋଗ କରାଯାଇ ମୋଟ ପରିବ୍ୟୟ ସ୍ଥିର କରାଯାଏ; ଯଥା-
ଉତ୍ପାଦର ପରିମାଣ ‘ଶୂନ୍ୟ’ ହେଲେ,
ମୋଟ ପରିବ୍ୟୟ = ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ (OF) + ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (0) = OF
ଉତ୍ପାଦର ପରିମାଣ OM ହେଲେ,
ମୋଟ ପରିବ୍ୟୟ = ସ୍ଥିର ପରିବ୍ୟୟ (MP) + ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (PR) = MR
ଉତ୍ପାଦର ପରିମାଣ ଠQ ହେଲେ,
ମୋଟ ପରିବ୍ୟୟ = ସ୍ଥିର ପରିବ୍ୟୟ (QK) + ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (KL) = QL
ମୋଟ ପରିବ୍ୟୟ = ସ୍ଥିର ପରିବ୍ୟୟ (QK) + ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (KL) = QL
ଉପରୋକ୍ତ ପର୍ଯ୍ୟାଲୋଚନାରୁ ଜଣାଯାଏ ଯେ, ସ୍ଵଳ୍ପକାଳରେ ମୋଟ ପରିବ୍ୟୟର ଦୁଇଟି ଉପାଂଶ ବା ଉପାଦାନ ରହିଛି । ତାହାକୁ ସ୍ଥିର ପରିବ୍ୟୟ ଓ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ନାମରେ ନାମିତ କରାଯାଇଛି । ଏହି ଦୁଇ ପରିବ୍ୟୟର ସମଷ୍ଟିରୁ ମୋଟ ପରିବ୍ୟୟ ସ୍ଥିର କରାଯାଇଥାଏ ।
2. ସ୍ଵଳ୍ପକାଳୀନ ମୋଟ ହାରାହାରି ବକ୍ରରେଖା କାହିଁକି (U) ଆକୃତିର – କାରଣ ଦର୍ଶାଅ
କିମ୍ବା, ସ୍ଵଳ୍ପକାଳୀନ ହାରାହାରି ପରିବ୍ୟୟ ରେଖାଗୁଡ଼ିକର ଆକୃତି କାରଣ ସହ ବର୍ଣନା କର ଓ ଏମାନଙ୍କ ମଧ୍ୟରେ କି ପ୍ରକାର ସଂପର୍କ ରହିଛି ?
କିମ୍ବା, ମୋଟ ହାରାହାରି ପରିବ୍ୟୟ କ’ଣ ? ଏହାର ଉପାଂଶଗୁଡ଼ିକ ବ୍ୟାଖ୍ୟା କରି ଏହା କିପରି ମୋଟ ହାରାହାରି ପରିବ୍ୟୟ ନିର୍ଦ୍ଧାରଣ କରନ୍ତି ଦର୍ଶାଅ ।
କିମ୍ବା, ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ ଓ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ । ଏହା କିପରି ମୋଟ ହାରାହାରି ପରିବ୍ୟୟ ନିର୍ଣ୍ଣୟ କରିଥାଏ ?
Answer:
ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ବ୍ୟୟ କରାଯାଉଥିବା ସମସ୍ତ ଅର୍ଥକୁ ମୋଟ ପରିବ୍ୟୟର ଆଖ୍ୟା ଦିଆଯାଇଥାଏ । ଏହାର ପରିମାଣ ଉତ୍ପାଦ ବୃଦ୍ଧିର ପରିମାଣ ସହ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହୋଇଥାଏ । ମାତ୍ର ସ୍ଵଳ୍ପକାଳରେ ମୋଟ ପରିବ୍ୟୟକୁ ମୋଟ ସ୍ଥିର ପରିଦ୍ୟାୟ ଓ ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟର ସମଷ୍ଟି କୁହାଯାଏ । ତେଣୁ ସ୍ଥିର ପରିବ୍ୟୟ ଓ ପରିବର୍ଭନୀୟ ପରିବ୍ୟୟ ମୋଟ ପରିବ୍ୟୟର ଦୁଇଟି ପ୍ରଧାନ ଅଂଶରୂପେ ବିବେଚିତ ହୁଏ।
ଏଠାରେ ଉଲ୍ଲେଖଯୋଗ୍ୟ ଯେ ଉତ୍ପାଦର ପରିମାଣ ବୃଦ୍ଧି ସହ ଏକକ ପିଛା ଉତ୍ପାଦନ ପରିବ୍ୟୟର ପରିବର୍ତ୍ତନ ଘଟିଥାଏ । କାରଣ ଉତ୍ପାଦର ଏକକ ବୃଦ୍ଧି ପାଇଲେ ଏକକ ପିଛା ସ୍ଥିର ପରିବ୍ୟୟ ଓ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟରେ ପରିବର୍ତ୍ତନ ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ଏସବୁ ତତ୍ତ୍ଵର ଆଲୋଚନା ହାରାହାରି ପରିବ୍ୟୟ ଅଭିଧାରଣା ମାଧ୍ୟମରେ କରାଯାଇପାରେ ।
ମୋଟ ହାରହାରି ପରିବ୍ୟୟ (Average Total Cost) (AC) :
ପ୍ରତି ଏକକ ଉତ୍ପାଦନ ପାଇଁ ଯେଉଁ ପରିବ୍ୟୟ ଉତ୍ପାଦନକର୍ତ୍ତା ବହନ କରିଥା’ନ୍ତି, ତାହାକୁ ହାରାହାରି ମୋଟ ପରିବ୍ୟୟ (AC) କୁହାଯାଏ । ଅର୍ଥାତ୍ ଏକକ ପ୍ରତି ଉତ୍ପାଦନ ପରିବ୍ୟୟକୁ ହାରାହାରି ମୋଟ ପରିବ୍ୟୟ କୁହାଯାଏ । ମୋଟ ପରିବ୍ୟୟ (AC) କୁ ଉତ୍ପାଦର ମୋଟ ପରିମାଣ (q) ସହ ଭାଗ କରି ହାରାହାରି ପରିବ୍ୟୟ ନିର୍ଣ୍ଣୟ କରାଯାଏ; ଯଥା –
ହାରାହାରି ମୋଟ ପରିବ୍ୟୟ (AC) = \(\frac{ମୋଟ ପରିବ୍ୟୟ (TC)}{ମୋଟ ଉତ୍ପାଦର ପରିମାଣ (q)}\)
ମୋଟ ହାରାହାରି ପରିବ୍ୟୟର ଆଲୋଚନା ସମୟରେ ଏହାର ଦୁଇ ପ୍ରଧାନ ଅଂଶ; ଯଥା – ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (Average Fixed Cost) ଓ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (Average Variable Cost) ଉପରେ ଗୁରୁତ୍ବ ଆରୋପ କରାଯାଇଥାଏ ।
ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (Average Fixed Cost) (AFC) :
ଏକକ ପ୍ରତି ବ୍ୟୟ କରାଯାଉଥବା ସ୍ଥିର ପରିବ୍ୟୟକୁ ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC) କୁହାଯାଏ । ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ସ୍ଵଳ୍ପକାଳରେ ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ସାମଗ୍ରିକଭାବେ ଅପରିବର୍ତ୍ତିତ ରହିଥାଏ । ତେଣୁ ଉତ୍ପାଦର ପରିମାଣ ବୃଦ୍ଧି ଘଟିଲେ ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟରେ କୌଣସି ବୃଦ୍ଧି ପରିଲକ୍ଷିତ ହୁଏ ନାହିଁ । ମାତ୍ର ସମପରିମାଣର ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ ଅଧିକ ସଂଖ୍ୟକ ଏକକ ମଧ୍ୟରେ ବଣ୍ଟିତ ହୋଇଯାଏ । ଫଳରେ ଉତ୍ପାଦର ଏକକ ପ୍ରତି ସ୍ଥିର ପରିବ୍ୟୟ ବା ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ ଉତ୍ପାଦନର ବୃଦ୍ଧି ସହ କ୍ରମଶଃ ହ୍ରାସ ପାଏ । ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟକୁ ମୋଟ ଉତ୍ପାଦଦ୍ୱାରା ବିଭାଜିତ କରି ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
ହାରାହରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC) = \(\frac{ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ (TFC)}{ମୋଟ ଉତ୍ପାଦର ପରିମାଣ (q)}\)
![]()
ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (Average Variable Cost) (AVC) :
ଉତ୍ପାଦର ଏକକ ପ୍ରତି ବ୍ୟୟ କରାଯାଉଥିବା ପରିବର୍ଭନୀୟ ପରିବ୍ୟୟକୁ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ କୁହାଯାଏ । ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟକୁ ମୋଟ ଉତ୍ପାଦନର ପରିମାଣଦ୍ୱାରା ବିଭାଜିତ କରି ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ନିର୍ଦ୍ଧାରଣ କରଯାଇଥାଏ; ଯଥା –
ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) = \(\frac{ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC)}{ମୋଟ ଉତ୍ପାଦର ପରିମାଣ (q)}\)
ଉତ୍ପାଦନର ବିଭିନ୍ନ ସ୍ତରରେ ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟରେ ବିଭିନ୍ନତା ଦେଖାଦିଏ । ଏହା ଉତ୍ପାଦନର ପରିମାଣ ଅନୁଯାୟୀ ଭିନ୍ନ ହୋଇଥାଏ । କିନ୍ତୁ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ହ୍ରାସମାନ ଉତ୍ପନ୍ନ ସୂତ୍ର ଅନୁସାରେ ହିଁ ହୋଇଥାଏ । ପ୍ରାଥମିକ ଅବସ୍ଥାରେ ଅର୍ଥାତ୍ ହ୍ରାସମାନ ଉତ୍ପନ୍ନ ସୂତ୍ରର ପ୍ରଥମ ପର୍ଯ୍ୟାୟରେ (କ୍ରମବର୍ଦ୍ଧିଷ୍ଣୁ ଉତ୍ପନ୍ନ ପର୍ଯ୍ୟାୟ ) ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ଉତ୍ପାଦନର ବୃଦ୍ଧି ସହିତ ହ୍ରାସ ପାଏ । ଅନ୍ୟ ପକ୍ଷରେ କ୍ରମହ୍ରାସମାନ ଉତ୍ପନ୍ନ ସୂତ୍ରର ଦ୍ବିତୀୟ ପର୍ଯ୍ୟାୟରେ ଏହା ଉତ୍ପାଦର ବୃଦ୍ଧି ସହିତ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହୋଇଥାଏ । ତେଣୁ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ରେଖା ଥାଳିଆ ଆକୃତି ପରି ପରିଦୃଷ୍ଟ ହୋଇଥାଏ ।
ଉପରୋକ୍ତ ଆଲୋଚନାରେ ହାରାହାରି ପରିବ୍ୟୟ (AC), ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC) ଓ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) ର ସମଷ୍ଟି ମାତ୍ର ।
ମୋଟ ହାରାହାରି ପରିବ୍ୟୟ (AC) = \(\frac{ମୋଟ ପରିବ୍ୟୟ (TC)}{ମୋଟ ଉତ୍ପାଦର ପରିମାଣ (q)}\)
⇒ AC = \(\frac{\mathrm{TC}}{\mathrm{q}}=\frac{\mathrm{TFC}+\mathrm{TVC}}{\mathrm{q}}\) (∴ TC = TFC + TVC)
⇒ AC = \(\frac{\text { TFC }}{q}+\frac{\text { TVC }}{\mathrm{q}}\) = AFC + AVC
କୌଣସି ଏକ ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ, ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ଓ ମୋଟ ପରିବ୍ୟୟର ଗତିବିଧି ଏକ ଗାଣିତିକ ବିଶ୍ଳେଷଣ ଓ ପୈଖ୍ୟକ ଉପସ୍ଥାପନାଦ୍ୱାରା ଆଲୋଚନା କରାଯାଇପାରେ ।
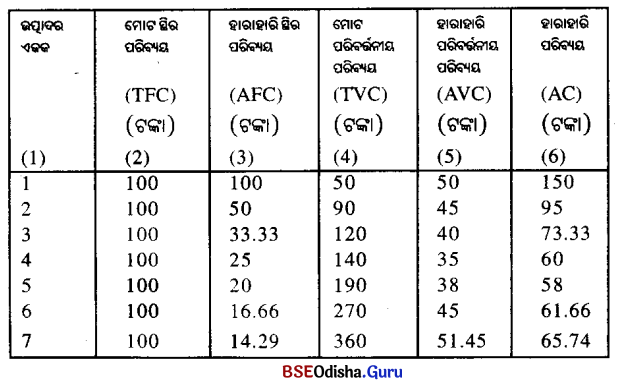
ଉପରୋକ୍ତ ଗାଣିତିକ ସାରଣୀରେ ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ, ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ଓ ମୋଟ ପରିବ୍ୟୟ ଗତିବିଧ୍ ଆଲୋଚିତ ହୋଇଛି ।
ସାରଣୀକୁ ଅନୁଧ୍ୟାନ କଲେ ପ୍ରତୀୟମାନ ହୁଏ ଯେ, ମୋଟ ସ୍ଥିର ପରିବ୍ୟୟ (TFC) ଉତ୍ପାଦନର ପରିମାଣ ନିର୍ବିଶେଷରେ ସ୍ଥିର ହୋଇରହିଛି (100) ଟଙ୍କା) । ମାତ୍ର ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC), ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ କ୍ରମାଗତଭାବେ ହ୍ରାସ ପାଇ ଚାଲିଛି । ଦ୍ୱିତୀୟରେ ମୋଟ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (TVC), ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହୋଇଚାଲିଛି । ମାତ୍ର ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) ପ୍ରଥମାବସ୍ଥାରେ (ଚତୁର୍ଥ ଏକକ ପର୍ଯ୍ୟନ୍ତ) ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ହ୍ରାସ ପାଇଛି (50 ଟଙ୍କାରୁ 35 ଟଙ୍କା) ଓ ପରବର୍ତ୍ତୀ ପର୍ଯ୍ୟାୟରେ (ପଞ୍ଚମ ଏକକଠାରୁ) ଏହା (AVC) ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହୋଇଛି ।
ମାତ୍ର ମୋଟ ହାରାହାରି ପରିବ୍ୟୟ (AC) ଏକାଦିକ୍ରମେ ପଞ୍ଚମ ଏକକ ପର୍ଯ୍ୟନ୍ତ ହ୍ରାସ ପାଇଛି ଓ ପରବର୍ତ୍ତୀ ପର୍ଯ୍ୟାୟରେ ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ବୃଦ୍ଧି ପାଇଛି । ସାରଣୀର ଷଷ୍ଠ ସ୍ତମ୍ଭର (AC), ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC) ତୃତୀୟ ସ୍ତମ୍ଭ ଓ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) ପଞ୍ଚମ ସ୍ତମ୍ଭର ଯୋଗଫଳ ।
AC = AFC + AVC
ନୈକ ଉପସ୍ଥାପନା :
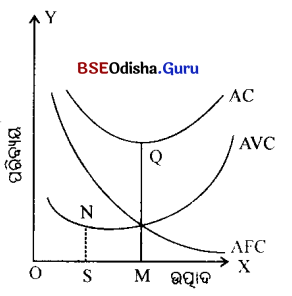
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ଉତ୍ପାଦର ପରିମାଣକୁ OX ଅକ୍ଷରେ ଓ ପରିବ୍ୟୟକୁ OY ଅକ୍ଷରେ ପରିମାପ କରାଯାଇଛି ।
ଏହି ଚିତ୍ରରେ ଗାଣିତିକ ସାରଣୀ ଭଳି ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC ଦ୍ଵାରା ଚିହ୍ନିତ) ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ କ୍ରମାଗତ ଭାବେ ହ୍ରାସ ପାଇଛି, ମାତ୍ର ଏହା OX ଅକ୍ଷକୁ ନାହିଁ । ତେଣୁ ଏଥୁରୁ ସୂଚିତ ହେଉଛି ଯେ AFC କଦାପି ଶୂନ୍ୟ ହେବ ନାହିଁ । ଦ୍ଵିତୀୟତଃ, ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) { ପ୍ରଥମ ଅବସ୍ଥାରେ ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ହ୍ରାସ ପାଉଛି ଓ ପରବର୍ତ୍ତୀ ପର୍ଯ୍ୟାୟରେ ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ବୃଦ୍ଧି ପାଉଛି ।
ସେହିପରି ମୋଟ ହାରାହାରି ପରିବ୍ୟୟ (AC) ପ୍ରାଥମିକ ଅବସ୍ଥାରେ ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ହ୍ରାସ ପାଉଛି । ଠୁ ଏହାର ସର୍ବନିମ୍ନ ବିନ୍ଦୁ । ମାତ୍ର OM ଉତ୍ପାଦର ପରିମାଣ ପରେ AC ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହୋଇଛି ।
ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC), ହାରହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) ଓ ମୋଟ ପରିବ୍ୟୟ (AC) ମଧ୍ଯରେ ସମ୍ପର୍କ :
AFC, AVC ଓ AC ମଧ୍ୟରେ ଥିବା ସଂପର୍କ ଉପରୋକ୍ତ ଗାଣିତିକ ସାରଣୀ ଓ ରେଖାଚିତ୍ରରେ ଅତ୍ୟନ୍ତ ସ୍ପଷ୍ଟ । ଗାଣିତିକ ସାରଣୀରେ ବିଶ୍ଳେଷଣ ଓ ରୈଖ୍ୟକ ଉପସ୍ଥାପନା ମଧ୍ୟରେ ସାଦୃଶ୍ୟ ପରିଲକ୍ଷିତ ହୋଇଥାଏ ।
ଉପରୋକ୍ତ ଦ୍ୱୈତ ଉପସ୍ଥାପନାରେ ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ନିୟମିତ ଭାବେ ହ୍ରାସ ପାଇଛି, ମାତ୍ର ଏହା OX ଅକ୍ଷକୁ ସ୍ପର୍ଶ କରୁନଥିବାରୁ AFC କଦାପି ‘ଶୂନ୍ୟ’ ହୁଏ ନାହିଁ । ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) ପ୍ରାଥମିକ ଅବସ୍ଥାରେ ସ୍ଥିର ଉପାଦାନର ଅସମ୍ପୂର୍ଣ୍ଣ ଉପଯୋଗ ଯୋଗୁଁ ଅଧିକ ହୋଇଥାଏ । ମାତ୍ର ଉତ୍ପାଦର ବୃଦ୍ଧି ଯୋଗୁଁ ପ୍ରତିଷ୍ଠାନ ବିଭିନ୍ନ ଆଭ୍ୟନ୍ତରୀଣ ସୁବିଧା ଉପଭୋଗ କରିଥାଏ ଯଦ୍ବାରା AVC କ୍ରମଶଃ ହ୍ରାସ ପାଏ । କିନ୍ତୁ AVC ସର୍ବନିମ୍ନ ବିନ୍ଦୁ (N) ରେ ପହଞ୍ଚିବା ପରେ ଏହା କ୍ରମଶଃ ବୃଦ୍ଧି ପାଏ । କାରଣ ଉତ୍ପାଦନ ପରିମାଣ ବୃଦ୍ଧିଜନିତ ପରିସ୍ଥିତିରେ ପ୍ରତିଷ୍ଠାନ କେତେକ ଅସୁବିଧାର ସମ୍ମୁଖୀନ ହୋଇଥାଏ । ଏହି କାରଣରୁ AVC ରେଖା ‘U’ ଆକୃତି ବିଶିଷ୍ଟ ହୋଇଥାଏ ।
![]()
AVC ରେଖାଭଳି AC ରେଖା ମଧ୍ଯ ‘U’ ଆକୃତିବିଶିଷ୍ଟ; ମାତ୍ର ଏହା AVC ରେଖାଭଳି ଅଧିକ ଚଟକା ହୋଇନଥାଏ । ସ୍ଵଳ୍ପକାଳୀନ ହାରାହାରି ପରିବ୍ୟୟ କାହିଁକି ‘U’ ଆକୃତିବିଶିଷ୍ଟ ତାହାର କାରଣ ନିମ୍ନରେ ପ୍ରଦାନ କରାଗଲା ।
ପ୍ରଥମତଃ, ହାରାହାରି ପରିବ୍ୟୟ (AC), ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC) ଓ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) ର ସମଷ୍ଟି ମାତ୍ର । ଉତ୍ପାଦନର ପ୍ରାରମ୍ଭିକ ପର୍ଯ୍ୟାୟରେ ଉଭୟେ AFC ଓ AVC ହ୍ରାସମାନ ଅବସ୍ଥାରେ ରହିଥା’ନ୍ତି (ଗାଣିତିକ ସାରଣୀ ଓ ରେଖାଚିତ୍ର ଦ୍ରଷ୍ଟବ୍ୟ) । ଗାଣିତିକ ସାରଣୀ ଅନୁସାରେ ଚତୁର୍ଥ ଏକକ ପର୍ଯ୍ୟନ୍ତ AVC ହ୍ରାସ ପାଇଛି । ସେହିପରି ରେଖାଚିତ୍ରରେ OS ଉତ୍ପାଦ ପର୍ଯ୍ୟନ୍ତ AVC ହ୍ରାସ ପାଇଛି । OS ଉତ୍ପାଦ ବା ଚତୁର୍ଥ ଏକକ ପରେ AVC ବୃଦ୍ଧି ପାଇବା ଆରମ୍ଭ ହୋଇଛି ।
କିନ୍ତୁ AFC କ୍ରମାଗତ ହ୍ରାସ ପାଇଛି । ଏଠାରେ ଉଲ୍ଲେଖଯୋଗ୍ୟ ଯେ, AFC ର ହ୍ରାସର ହାର AVC ର ବୃଦ୍ଧିର ହାରଠାରୁ ବୃହତ୍ତର । ତେଣୁ AVC ବୃଦ୍ଧି ପାଇବା ସତ୍ତ୍ବେ ମୋଟ ହାରାହାରି ପରିବ୍ୟୟ (AC) ହ୍ରାସ ପାଇଥାଏ । ରେଖାଚିତ୍ରରେ OM ଉତ୍ପାଦ ପର୍ଯ୍ୟନ୍ତ AC ହ୍ରାସ ପାଉଥିବା ସ୍ଥଳେ AVC, OS ଉତ୍ପାଦ ପର୍ଯ୍ୟନ୍ତ ହ୍ରାସ ପାଇଛି । ତେଣୁ AC ର ସର୍ବନିମ୍ନ ବିନ୍ଦୁ (Q), AVC ର ସର୍ବନିମ୍ନ ବିନ୍ଦୁ (N) ର ଡାହାଣକୁ ଅବସ୍ଥିତ ।
ଏ ପ୍ରସଙ୍ଗରେ ଦୁଇଟି କାରଣ ଉଲ୍ଲେଖଯୋଗ୍ୟ । AVC ରେଖାର ନିମ୍ନତମ ବିନ୍ଦୁ (N), AC, ରେଖାର ନିମ୍ନତମ ବିନ୍ଦୁ (Q) ଅପେକ୍ଷା ପୂର୍ବରୁ ପହଞ୍ଚେ । ଦ୍ୱିତୀୟତଃ, AVC, AC ରେଖାର ଯେତେ ନିକଟବର୍ତ୍ତୀ ହେଲେହେଁ ତାହାକୁ ସ୍ପର୍ଶ କରେ ନାହିଁ । ହାରାହାରି ପରିବ୍ୟୟ (AC) ରେଖା ଓ AVC ରେଖା ମଧ୍ୟରେ ଦୂରତ୍ୱ AFC ର ପରିମାପକ ଅଟେ । AFC ଶୂନ୍ୟ ହେଉନଥିବାରୁ AVC ରେଖା ଓ AC ରେଖା ମଧ୍ୟରେ ସର୍ବଦା ସମଦୂରତ୍ୱ ବଜାୟ ରହେ ଓ ସେମାନେ ପରସ୍ପରକୁ ଛେଦ କରନ୍ତି ନାହିଁ ।
ଦଉପାଦାନ ଅପରିବର୍ତ୍ତିତ ରହୁଥିବାରୁ ପରିବର୍ତ୍ତନୀୟ ଉପାଦାନର ଉପଯୋଗକୁ ହ୍ରାସ-ବୃଦ୍ଧି କରାଯାଇ ମୋଟ ଉତ୍ପାଦନର ହ୍ରାସ-ବିତୀୟତଃ, ସ୍ଵଳ୍ପକାଳୀନ ହାରାହାରି ପରିବ୍ୟୟ ରେଖା ପରିବର୍ତ୍ତନୀୟ ଅନୁପାତ ସୂତ୍ରର ଅଧୀନ । ସ୍ଵଳ୍ପକାଳରେ ସ୍ଥିର ବୃଦ୍ଧି କରାଯାଇପାରେ । ତେଣୁ ପରିବର୍ଭନୀୟ ସୂତ୍ର ବିଶେଷ ଭାବରେ କାର୍ଯ୍ୟକରେ । ଯାହା ଫଳରେ ପ୍ରାଥମିକ ପର୍ଯ୍ୟାୟରେ କ୍ରମବର୍ଦ୍ଧିଷ୍ଣୁ ଉତ୍ପନ୍ନ ସୂତ୍ର ଏବଂ ପରବର୍ତ୍ତୀ ପର୍ଯ୍ୟାୟରେ କ୍ରମହ୍ରାସମାନ ଉତ୍ପନ୍ନ ସୂତ୍ରର ବଶବର୍ତ୍ତୀ ହୋଇ AC ପ୍ରଥମରୁ ହ୍ରାସ ପାଇ ପରେ ବୃଦ୍ଧି ପାଇଥାଏ । ତେଣୁ ଏହାର ଆକୃତି ‘U’ ଆକାରର ହୋଇଥାଏ ।
ତୃତୀୟତଃ, ସ୍ୱଳ୍ପକାଳରେ ସ୍ଥିର ଉପାଦାନ ଅବିଭାଜ୍ୟ ହୋଇଥିବାରୁ ପ୍ରଥମ ଅବସ୍ଥାରେ ଏହାର ପୂର୍ଣ୍ଣ ବିନିଯୋଗ ହୋଇପାରି ନଥାଏ । ଉତ୍ପାଦର ପରିମାଣ ସଂପ୍ରସାରିତ ହେଲେ ଏହି ଅବିଭାଜ୍ୟ ଉପାଦାନଗୁଡ଼ିକୁ ଯଥାର୍ଥ ଉପଯୋଗ କରାଯାଇଥାଏ । ତେଣୁ ହାରାହାରି ପରିବ୍ୟୟ ହ୍ରାସମାନ ହୋଇଥାଏ । ମାତ୍ର ସର୍ବୋତ୍ତମ ଉତ୍ପାଦ ସ୍ତର ଅତିକ୍ରମ ହେଲେ ହାରାହାରି ପରିବ୍ୟୟ ବୃଦ୍ଧି ପାଏ । ତେଣୁ AC ରେଖା ‘U’ ଆକୃତିବିଶିଷ୍ଟ ହୋଇଥାଏ ।
3. ଉତ୍ପାଦନ ପରିବ୍ୟୟ କହିଲେ କ’ଣ ବୁଝାଏ ? ହାରାହାରି ପରିବ୍ୟୟ ଓ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ଦର୍ଶାଅ ।
Answer:
ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ନିୟୋଜିତ ହେଉଥିବା ସମସ୍ତ ଉପାଦାନ; ଯଥା- ଭୂମି, ଶ୍ରମ ଓ ପୁଞ୍ଜି ନିମନ୍ତେ ଉତ୍ପାଦନକର୍ତ୍ତା ଏହାର ମାଲିକମାନଙ୍କୁ ଯେଉଁ ପାରିତୋଷିକ ପ୍ରଦାନ କରନ୍ତି ତାହାକୁ ‘ଉତ୍ପାଦନ ପରିବ୍ୟୟ’ କୁହାଯାଏ । ସରଳ ଭାଷାରେ, ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଉତ୍ପାଦନକର୍ତ୍ତାଙ୍କଦ୍ବାରା ବହନ କରାଯାଉଥିବା ସାମଗ୍ରିକ ବ୍ୟୟକୁ ଉତ୍ପାଦନ ପରିବ୍ୟୟ କୁହାଯାଏ । ମୋଟ ଉପରେ ଉତ୍ପାଦନ ଉଦ୍ଦେଶ୍ୟରେ କରାଯାଉଥିବା ବ୍ୟୟକୁ ଉତ୍ପାଦନ ପରିବ୍ୟୟ କୁହାଯାଏ ।
ଉତ୍ପାଦନ ପରିବ୍ୟୟକୁ ସାଧାରଣତଃ ତିନୋଟି ଦୃଷ୍ଟିକୋଣରୁ ବିଚାର କରାଯାଇଥାଏ; ଯଥା- ମୌଦ୍ରିକ ପରିବ୍ୟୟ, ବାସ୍ତବ ପରିବ୍ୟୟ ଓ ବିକଳ୍ପ (ସୁଯୋଗ ) ପରିବ୍ୟୟ ।
ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣର ଉତ୍ପାଦନ ନିମନ୍ତେ ବହନ କରାଯାଉଥିବା ସମସ୍ତ ବ୍ୟୟର ସମଷ୍ଟିକୁ ମୋଟ ପରିବ୍ୟୟର ଆଖ୍ୟା ଦିଆଯାଇଥାଏ । ଏହି ମୋଟ ପରିବ୍ୟୟ ଉତ୍ପାଦନର ବୃଦ୍ଧି ସହ ବୃଦ୍ଧି ପାଇଥାଏ ।
ହାରାହାରି ପରିବ୍ୟୟ- ପ୍ରତି ଏକକ ଉତ୍ପାଦ ପାଇଁ ଉତ୍ପାଦନ ପରିବ୍ୟୟକୁ ହାରାହାରି ପରିବ୍ୟୟ କୁହାଯାଇଥାଏ । ଅନ୍ୟ ଅର୍ଥରେ ପ୍ରତି ଏକକ ଉତ୍ପାଦନ ପାଇଁ ବହନ କରାଯାଉଥିବା ପରିବ୍ୟୟକୁ ହାରାହାରି ପରିବ୍ୟୟ କୁହାଯାଇଥାଏ । ମୋଟ ପରିବ୍ୟୟକୁ ମୋଟ ଉତ୍ପାଦର ପରିମାଣଦ୍ୱାରା ବିଭାଜିତ କରି ହାରାହାରି ପରିବ୍ୟୟ ନିର୍ଣ୍ଣୟ କରାଯାଇଥାଏ; ଯଥା-
ହାରାହାରି ପରିବ୍ୟୟ (AC) = \(\frac{ମୋଟ ପରିବ୍ୟୟ (TC)}{ମୋଟ ଉତ୍ପାଦ (q)}\)
ହାରାହାରି ପରିବ୍ୟୟର ଦୁଇଟି ପ୍ରଧାନ ଉପାଂଶ; ଯଥା- ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC) ଓ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC) ରହିଛି । ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ (AFC) ଓ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ (AVC)ର ସମଷ୍ଟିଦ୍ୱାରା ହାରାହାରି ପରିବ୍ୟୟ (AC) ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
i.e. AC = AFC + AVC
ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ (Marginal Cost MC) :
ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ କୌଣସି ଦ୍ରବ୍ୟର ଅତିରିକ୍ତ ଏକକ ଉତ୍ପାଦନ ଫଳରେ ମୋଟ ପରିବ୍ୟୟ ଯେଉଁ ପରିମାଣରେ ବୃଦ୍ଧି ପାଏ ତାହାକୁ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ (MC) କୁହାଯାଏ । ଅନ୍ୟ ଅର୍ଥରେ ଦ୍ରବ୍ୟର ଅତିରିକ୍ତ ଏକକ ଉତ୍ପାଦନ ଫଳରେ ଉପସ୍ଥିତ ମୋଟ ପରିବ୍ୟୟ ଓ ଏହାର ପୂର୍ବ ଏକକ ପାଇଁ ମୋଟ ପରିବ୍ୟୟ ମଧ୍ୟରେ ଯେଉଁ ପାର୍ଥକ୍ୟ ଦେଖାଯାଏ, ତାହାକୁ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ କୁହାଯାଏ ।
i.e. MCn = TCn – TCn-1
n → ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟର ଏକକ ।
ଅନ୍ୟ ଅର୍ଥରେ MC = \(\frac{ΔΤC}{Δq}\) = \(\frac{ମୋଟ ପରିବ୍ୟୟରେ ପରିବର୍ତ୍ତନ }{ଉତ୍ପାଦରେ ପରିବର୍ତ୍ତନ}\)
![]()
ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ସର୍ବଦା ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ସହ ସଂଶ୍ଳିଷ୍ଟ ଓ ଏହା ସ୍ଥିର ପରିବ୍ୟୟ ସହ ସଂପର୍କିତ ନୁହେଁ ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ଏହାର ହାରାହାରି ପରିବ୍ୟୟ ଓ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟର ଆଚରଣରେ ଭିନ୍ନତା ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ଏତଦ୍ବ୍ୟତୀତ, ହାରାହାରି ପରିବ୍ୟୟ (AC) ଓ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ମଧ୍ୟରେ ଏକ ସଂପର୍କ ରହିଛି । ନିମ୍ନଲିଖୂ ଗାଣିତିକ ସାରଣୀ ଓ ରେଖାଚିତ୍ରରୁ ଦୁହିଁଙ୍କ ମଧ୍ୟରେ ଥିବା ସଂପର୍କର ସ୍ପଷ୍ଟ ଚିତ୍ର ମିଳିପାରେ ।
ଗାଣିତିକ ବିଶ୍ଳେଷଣ :
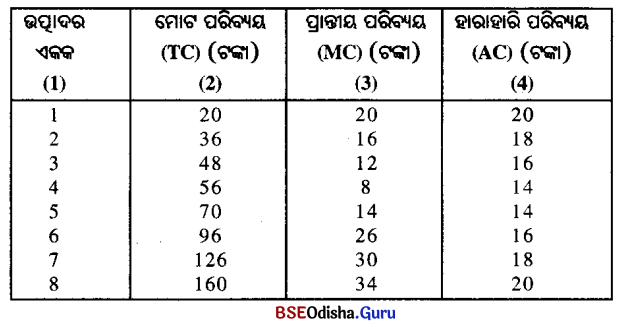
ଉପରୋକ୍ତ ସାରଣୀରେ ଉପସ୍ଥାପିତ ତଥ୍ୟରୁ ପ୍ରତୀୟମାନ ହୁଏ ଯେ ମୋଟ ପରିବ୍ୟୟ (ସ୍ତମ୍ଭ 2) ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ବୃଦ୍ଧି ପାଉଛି । ଏହି ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ପ୍ରାଥମିକ ଅବସ୍ଥାରେ ଚତୁର୍ଥ ଏକକ ଉତ୍ପାଦନ ପର୍ଯ୍ୟନ୍ତ ହ୍ରାସ ପାଇଛି (ସ୍ତମ୍ଭ -3) । ଏହାର ଅନୁରୂପ ହାରାହାରି ପରିବ୍ୟୟ ମଧ୍ୟ ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ହ୍ରାସ ପାଇଛି । ମାତ୍ର ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟର ହ୍ରାସ ହେବା ହାର ହାରାହାରି ପରିବ୍ୟୟର ହ୍ରାସ ହେବା ହାରଠାରୁ ଅଧିକ ।
ପଞ୍ଚମ ଏକକ ଉତ୍ପାଦନ ହେବା ଅବସ୍ଥାରେ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ (MC) ଓ ହାରାହାରି ପରିବ୍ୟୟ (AC) ପରସ୍ପର ସମାନ । ଏହାର ପରବର୍ତ୍ତୀ ପର୍ଯ୍ୟାୟରେ ଅର୍ଥାତ୍ ଷଷ୍ଠ ଏକକଠାରୁ ଉତ୍ପାଦର ବୃଦ୍ଧି ସହ ମୋଟ ପରିବ୍ୟୟ (ସ୍ତମ୍ଭ-2), ହାରାହାରି ପରିବ୍ୟୟ (ସ୍ତମ୍ଭ-4) ଓ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ (ସ୍ତମ୍ଭ -3) ବୃଦ୍ଧି ପାଇଛି । ମାତ୍ର ହାରାହାରି ପରିବ୍ୟୟ ବୃଦ୍ଧି ହାରଠାରୁ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ବୃଦ୍ଧିର ହାର ଅଧିକ ।
ବୈଖ୍ୟକ ଉପସ୍ଥାପନ :
ନିମ୍ନସ୍ଥ ଚିତ୍ରରେ ଉତ୍ପାଦର ପରିମାଣ OX– ଅକ୍ଷରେ ଓ ପରିବ୍ୟୟର ପରିମାଣ OY– ଅକ୍ଷରେ ପରିମାପ କରାଯାଇଛି । AC ରେଖା ହାରାହାରି ପରିବ୍ୟୟକୁ ଓ MC ରେଖା ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟକୁ ଚିହ୍ନିତ କରୁଅଛି ।
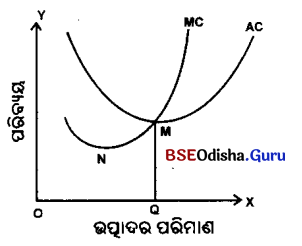
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରକୁ ବିଶ୍ଳେଷଣ କଲେ ଜଣାଯାଏ ଯେ, ଉତ୍ପାଦନର ପ୍ରାରମ୍ଭିକ ଅବସ୍ଥାରେ ହାରାହାରି ପରିବ୍ୟୟ ଓ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ହ୍ରାସ ପାଇଥାଏ । ମାତ୍ର ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟର ହ୍ରାସର ହାର ହାରାହାରି ପରିବ୍ୟୟର ହ୍ରାସର ହାରଠାରୁ ଅଧ୍ଵ । ତେଣୁ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ସର୍ବପ୍ରଥମେ ଏହାର ସର୍ବନିମ୍ନ ବିନ୍ଦୁ (N) ହାସଲ କରିଥାଏ ଯେଉଁ ସମୟରେ କି AC ରେଖା ହ୍ରାସମାନ ଅବସ୍ଥାରେ ରହିଥାଏ । AC ରେଖାର ସର୍ବନିମ୍ନ ବିନ୍ଦୁ ‘M’ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ରେଖାର ଡାହାଣକୁ ଅବସ୍ଥିତ ।
ଉତ୍ପାଦର ପରିମାଣ OQ ଥିବାବେଳେ ସୀମାନ୍ତ ପରିବ୍ୟୟ ଓ ହାରାହାରି ପରିବ୍ୟୟ ପରସ୍ପର ସମାନ ହୋଇଥା’ନ୍ତି (M ବିନ୍ଦୁ) ।
ଏହାର ପରବର୍ତ୍ତୀ ପର୍ଯ୍ୟାୟରେ (OQ ଉତ୍ପାଦ ପରେ) ପ୍ରାନ୍ତୀୟ ଉତ୍ପାଦର ବୃଦ୍ଧିର ହାର ହାରାହାରି ଉତ୍ପାଦର ବୃଦ୍ଧିର ହାରଠାରୁ ଅଧ୍ଵ । ଫଳରେ MC ରେଖା AC ରେଖାର ଊର୍ଦ୍ଧ୍ବରେ ଅବସ୍ଥିତ ।
ଗାଣିତିକ ବା ଜ୍ୟାମିତିକ ଦୃଷ୍ଟିକୋଣରୁ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ (MC) ଓ ହାରାହାରି ପରିବ୍ୟୟ (AC) ମଧ୍ୟରେ ଥିବା ନିମ୍ନଲିଖୂ ସଂପର୍କ ଦୃଷ୍ଟିଗୋଚର ହୋଇଥାଏ ।
(1) ହାରାହାରି ପରିବ୍ୟୟ ଓ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ଉଭୟେ ମୋଟ ପରିବ୍ୟୟରୁ ହିଁ ନିର୍ଣ୍ଣୟ କରାଯାଇଥା’ନ୍ତି । ହାରାହାରି ପରିବ୍ୟୟ କ୍ଷେତ୍ରରେ ମୋଟ ପରିବ୍ୟୟକୁ ମୋଟ ଉତ୍ପାଦରେ ବିଭାଜିତ କରାଯାଇଥାଏ; ଯଥା-
AC = \(\frac{TC}{q}\)
ଏବଂ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ କ୍ଷେତ୍ରରେ ମୋଟ ପରିବ୍ୟୟର ପରିବର୍ତ୍ତନକୁ ଉତ୍ପାଦର ପରିବର୍ତ୍ତନଦ୍ୱାରା ବିଭାଜିତ କରାଯାଇଥାଏ; ଯଥା-
MC = \(\frac{ΔTC}{Δq}\)
କିମାୃ, MCn = TCn – TCn-1,
(2) ଉଭୟ ଗାଣିତିକ ବିଶ୍ଳେଷଣ ଓ ରେଖାଚିତ୍ରରୁ ଏହା ପ୍ରତିଫଳିତ ହୁଏ ଯେ ଯେଉଁ ଉତ୍ପାଦର ସ୍ତର ପର୍ଯ୍ୟନ୍ତ ହାରାହାରି ପରିବ୍ୟୟ ହ୍ରାସ ପାଉଥାଏ ସେହି ଅବସ୍ଥାରେ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ରେଖା, ହାରାହାରି ପରିବ୍ୟୟ ରେଖାର ନିମ୍ନରେ ଅବସ୍ଥାନ କରେ ବା AC > MC କାରଣ ହାରାହାରି ପରିବ୍ୟୟ, ହାରାହାରି ସ୍ଥିର ପରିବ୍ୟୟ ଓ ହାରାହାରି ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟର ସମଷ୍ଟି ହୋଇଥିବାସ୍ଥଳେ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ କେବଳ ପରିବର୍ତ୍ତନୀୟ ପରିବ୍ୟୟ ସହ ସଂପୃକ୍ତ ।
(3) ଉପରୋକ୍ତ ବିଶ୍ଳେଷଣରୁ ସ୍ପଷ୍ଟ ଯେ, ଯେଉଁ ଉତ୍ପାଦର ସ୍ତରରେ ହାରାହାରି ପରିବ୍ୟୟ ବୃଦ୍ଧି ପାଏ (OQ ଉତ୍ପାଦର ପରବର୍ତୀ ଅବସ୍ଥା), ସେହି ସ୍ତରରେ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ମଧ୍ୟ ବୃଦ୍ଧି ପାଏ; ମାତ୍ର ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟର ବୃଦ୍ଧିର ହାର, ହାରାହାରି ପରିବ୍ୟୟର ବୃଦ୍ଧିର ହାରଠାରୁ ଅଧିକ ।
(4) ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ରେଖା, ହାରାହାରି ପରିବ୍ୟୟ ରେଖାର ସର୍ବନିମ୍ନ ବିନ୍ଦୁରେ ଛେଦ କରିଥାଏ (ଚିତ୍ରରେ M ବିନ୍ଦୁ) ଓ ଗାଣିତିକ ସାରଣୀରେ (ପଞ୍ଚମ ଏକକ)। ଏ କ୍ଷେତ୍ରରେ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ଚେଖାର ସର୍ବନିମ୍ନ ବିନ୍ଦୁ (N), ହାରାହାରି ପରିବ୍ୟୟ ରେଖାର ସର୍ବନିମ୍ନ ବିନ୍ଦୁ (M)ଠାରୁ ସଅଳ ଘଟିଥାଏ ।
(5) ହାରାହାରି ପରିବ୍ୟୟ (AC) ଓ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ (MC) ମଧ୍ୟରେ ପାରସ୍ପରିକ ସଂପର୍କ ରହିଛି । ଯେତେବେଳେ MC > AC ବା ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ରେଖା, ହାରାହାରି ପରିବ୍ୟୟ ରେଖାର ଊର୍ଦ୍ଧ୍ବରେ ରହିଥାଏ, ସେ ଅବସ୍ଥାରେ ହାରାହାରି ପରିବ୍ୟୟର ବୃଦ୍ଧି ପ୍ରକ୍ରିୟା ଜାରି ରହିଥାଏ । ଅନ୍ୟପକ୍ଷରେ, ଯେତେବେଳେ AC > MC, ସେ ଅବସ୍ଥାରେ ହାରାହାରି ପରିବ୍ୟୟରେ ହ୍ରାସମାନ ଲକ୍ଷଣ ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ପରିଶେଷରେ ଯେତେବେଳେ AC = MC, ହାରାହାରି ପରିବ୍ୟୟରେ ସ୍ଥିରତା ପ୍ରତିଫଳିତ ହୋଇଥାଏ ।
ଉପରୋକ୍ତ ଆଲୋଚନା ଆର୍ଥନୀତିକ ଦୃଷ୍ଟିକୋଣରୁ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ।
