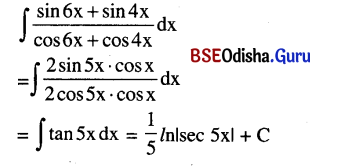CHSE Odisha Class 12 Math Solutions Chapter 11 Differential Equations Additional Exercise

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 11 Differential Equations Additional Exercise Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 11 Differential Equations Additional Exercise

(A) Multiple Choice Questions (Mcqs) With Answers

Question 1.
If f is an odd function, then write the value of \(\int_{-a}^a \frac{f(\sin x)}{f(\cos x)+f\left(\sin ^2 x\right)}\) dx
(a) 1
(b) 0
(c) -1
(d) 2
Solution:
(b) 0

Question 2.
If p and q are respectively degree and order of the differential equation y = e^dy/dx then write the relation between p and q.
(a) p ≠ q
(c) p ≡ q
(b) p = q
(d) None of these
Solution:
(b) p = q

Question 3.
Write the value of \(\int_0^1\){x} dx where {x} stands for fractional part of x.
(a) \(\frac{1}{2}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{2}{3}\)
Solution:
(a) \(\frac{1}{2}\)

Question 4.
Write the value of:
\(\int_0^{\pi / 2} \frac{\sin x}{\sin x+\cos x}\) dx – \(\int_0^{\pi / 2} \frac{\cos x}{\sin x+\cos x}\) dx
(a) 1
(b) 2
(c) 0
(d) π
Solution:
(c) 0

Question 5.
Write the value of \(\int_{\frac{\pi}{4}}^{\frac{\pi}{4}}\)sin⁵ x cos x dx
(a) 0
(b) 1
(c) cos x
(d) sin x
Solution:
(a) 0

Question 6.
Write the particular solution of the equation \(\frac{d y}{d x}\) = sin x given that y(π) = 2
(a) y = cos x + 1
(b) y = -cos x + 1
(c) y = -cos x – 1
(d) y = -sin x + 1
Solution:
(b) y = -cos x + 1

Question 7.
Write the degree of the following differential equation:
\(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\) = \(\frac{2 y^3+\left(\frac{d y}{d x}\right)^4}{\sqrt{\frac{d^2 y}{d x^2}}}\)
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(d) 3

Question 8.
Write the order ofthe following differential equation:
\(\frac{d^2 y}{d x^2}\) = \(\frac{2 y^3+\left(\frac{d y}{d x}\right)^4}{\sqrt{\frac{d^2 y}{d x^2}}}\)
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(c) 2

Question 9.
What is F(x) if F(x) = \(\int_0^x\)e^2t sin 3t dt?
(a) e^2x sin 3x
(b) e^2x cos 3x
(c) e^x sin 3x
(d) e^2x sin x
Solution:
(a) e^2x sin 3x

Question 10.
\(\int \frac{d x}{\cos ^2 x \sin ^2 x}\) = ?
(a) -2 cos 2x + C
(b) -2 cot 2x + C
(c) -2 sin 2x + C
(d) 2 cot 2x + C
Solution:
(b) -2 cot 2x + C

Question 11.
If \(\int_1^2\)f(x) dx= λ, then what is the value of \(\)f(3 – x) dx?
(a) λ
(b) λ²
(c) 1λ
(d) 2λ
Solution:
(a) λ

Question 12.
What is the value of \(\int_{-1}^1 \frac{d x}{1+x^2}\)?
(a) \(\frac{2 \pi}{2}\)
(b) 2π
(c) π
(d) \(\frac{\pi}{2}\)
Solution:
(d) \(\frac{\pi}{2}\)

Question 13.
Write the order of the following differential equation:
\(\frac{d^3 y}{d x^3}\) = \(\left(\frac{d^2 y}{d x^2}\right)^2\) + \(\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^4\) + y
(a) 1
(b) 3
(c) 2
(d) 0
Solution:
(b) 3

Question 14.
Write the degree of the following differential equation:
\(\frac{d^3 y}{d x^3}\) = \(\left(\frac{d^2 y}{d x^2}\right)^2\) + \(\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^4\) + y
(a) 1
(b) 2
(c) 3
(d) 0
Solution:
(a) 1

Question 15.
Write the particular solution of \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = (1 + x)⁴, y = 0 when x = -1.
(a) y = \(\frac{(1+x)^2}{5}\)
(b) y = \(\frac{(2+x)^5}{5}\)
(c) y = \(\frac{(1-x)^5}{5}\)
(d) y = \(\frac{(1+x)^5}{5}\)
Solution:
(d) y = \(\frac{(1+x)^5}{5}\)

Question 16.
Evaluate the integral ∫2x cosec² x² dx?
(a) cot x² + C
(b) -cot x² + C
(c) -cot 2x² + C
(d) cot 2x² + C
Solution:
(b) -cot x² + C

Question 17.
What is the value of \(\frac{d}{d x} \int_{250}^{300}\left(x^4+5 x^3\right)^2\) dx
(a) 0
(b) 1
(c) -1
(d) 2
Solution:
(a) 0

Question 18.
Write down the integral of ∫\(e^{x^2}\) 2x dx.
(a) \(e^{2 x^2}\)
(b) 2\(e^{2 x^2}\)
(c) \(e^{x^2}\)
(d) None of the above
Solution:
(c) \(e^{x^2}\)

Question 19.
What is the integral of ∫log e^x dx?
(a) \(\frac{2 x^2}{2}\) + C
(b) \(\frac{2 x^2}{3}\) + C
(c) \(\frac{x^2}{2}\) + C
(d) None of the above
Solution:
(c) \(\frac{x^2}{2}\) + C

Question 20.
What is the value of \(\int_{-2}^2\)|x| dx?
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(a) 0

Question 21.
\(\int_{-1}^1\)|1 – x| dx = ______.
(a) 0
(b) 1
(c) 2
(d) -1
Solution:
(c) 2

Question 22.
If ∫x³\(e^{c x^4}\)dx = \(\frac{1}{20} \mathrm{e}^{\mathrm{cx}}\) then C = ______.
(a) 0
(b) 2
(c) 4
(d) 5
Solution:
(d) 5

Question 23.
\(\int_a^b\)f(x) dx = 1 ⇒ \(\int_a^b\)k f(t)dt ______.
(a) k
(b) -k
(c) 2k
(d) None of the above
Solution:
(b) -k

Question 24.
\(\int_{-1}^1\)f(x) dx = k and f is an even function then \(\int_{-1}^1\)f(x) = ______.
(a) k
(b) -k
(c) 2k
(d) None of the above
Solution:
(c) 2k

Question 25.
If ∫\(\int_0^1\)f(x) dx = 4, \(\int_0^2\)f(t) dt and \(\int_4^2\)f(u) du = 1 then \(\int_1^4\)f(x) dx = ______.
(a) 0
(b) 1
(c) 3
(d) -3
Solution:
(d) -3

Question 26.
I(f) = \(\int_a^x\)f(t) dt and Df = f'(x) then (ID – DI) f = ______.
(a) -f(a)
(b) 2f(a)
(c) f(a)
(d) None of the above
Solution:
(a) -f(a)

Question 27.
\(\int_0^\pi\)cos¹⁰¹ x dx = ______.
(a) 0
(b) 1
(c) -1
(d) 101
Solution:
(a) 0

Question 28.
Let f satisfies all the conditions of Rolle’s theorem in [1, 6] then \(\int_1^6\)f'(x) dx = ______.
(a) 0
(b) 1
(c) -1
(d) 6
Solution:
(a) 0

Question 29.
\(\int_{-2}^2\)|x| dx = ______.
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(d) 4

Question 30.
Integrate ∫log x dx
(a) x. log x + x + C
(b) x. log x – x + C
(c) log x – x + C
(d) None of these
Solution:
(b) x. log x – x + C

Question 31.
Evaluate \(\int_0^2\)[x – 1] dx
(a) 0
(b) 1
(c) -1
(d) 2
Solution:
(b) 1

Question 32.
What is the value of: ∫\(\frac{f^{\prime}(x)-f(x)}{e^x}\) dx?
(a) e^x f(x) + C.
(b) e^2x f(x) + C.
(c) e^-x f(x) + C.
(d) None of the above
Solution:
(c) e^-x f(x) + C.

Question 33.
What is the value of \(\int_0^1\)x(1 – x)⁹⁹ dx?
(a) \(\frac{1}{100}\)
(b) \(\frac{1}{10}\)
(c) \(\frac{1}{1010}\)
(d) \(\frac{1}{10100}\)
Solution:
(d) \(\frac{1}{10100}\)

Question 34.
Solution of \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = xy + x + y + 1 is ______.
(a) 2x + \(\frac{x^2}{2}\) + C
(b) x + \(\frac{x}{2}\) + C
(c) x + \(\frac{2 x^2}{2}\) + C
(d) x + \(\frac{x^2}{2}\) + C
Solution:
(d) x + \(\frac{x^2}{2}\) + C

Question 35.
f(x) = \(\int_0^x\)t sin t dt then f ‘(x) = ______.
(a) x cos x
(b) x sin t
(c) x sin x
(d) x tan x
Solution:
(c) x sin x

Question 36.
What is the value of the integral \(\int_a^b \frac{|x|}{x}\)dx?
(a) |b| – |a|
(b) |a| – |b|
(c) |b| + |a|
(d) |a| + |b|
Solution:
(a) |b| – |a|

Question 37.
What is the value of ∫x^x (1 + ln x) dx?
(a) x^2x + C
(b) x^x + C
(c) 2x^x + C
(d) x² + C
Solution:
(b) x^x + C

Question 38.
Evaluate: \(\int_0^{\mathrm{p} / 2}\)ln(cot x) dx.
(a) 0
(b) 1
(c) cot x
(d) sin x
Solution:
(a) 0

Question 39.
Evaluate: \(\int_{-3}^4\)|x| dx
(a) \(\frac{2}{25}\)
(b) \(\frac{25}{2}\)
(c) \(\frac{25}{4}\)
(d) \(\frac{25}{-3}\)
Solution:
(b) \(\frac{25}{2}\)

Question 40.
Evaluate: \(\int_0^{\frac{\pi}{2}}\)(cos x – sin x) dx
(a) 0
(b) 1
(c) -1
(d) π
Solution:
(a) 0

Question 41.
Evaluate: \(\int_0^{\frac{\pi}{2}}\)log tan x dx.
(a) 1
(b) -1
(c) 0
(d) π
Solution:
(c) 0

Question 42.
Integrate: \(\frac{d x}{3 e^x-1}\)
(a) \(\ln \left(\frac{e^{3 x}-1}{e^x}\right)\) + C
(b) \(\ln \left(\frac{3 e^x+1}{e^x}\right)\) + C
(c) \(\ln \left(\frac{3 e^x-1}{e^x}\right)\) + C
(d) \(\ln \left(\frac{3 e^x+1}{e^{3 x}}\right)\) + C
Solution:
(c) \(\ln \left(\frac{3 e^x-1}{e^x}\right)\) + C

Question 43.
Evaluate: \(\int_0^1 \ln \left(\frac{1}{x}-1\right)\)dx
(a) 1
(b) 2
(c) 0
(d) -1
Solution:
(c) 0

Question 44.
Evaluate: ∫e^x\(\left(\frac{1-\sin x}{1-\cos x}\right)\)dx
(a) -e^x cot\(\frac{x}{2}\) + C
(b) e^x tan\(\frac{x}{2}\) + C
(c) e^x cot\(\frac{x}{2}\) + C
(d) -e^x sin\(\frac{x}{2}\) + C
Solution:
(a) -e^x cot\(\frac{x}{2}\) + C

Question 45.
Evaluate: \(\int_0^1\)x log(1 + x) dx
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{2}{3}\)
Solution:
(b) \(\frac{1}{4}\)

Question 46.
What is the integrating factor of the equation y’ + y cot x = cosec x?
(a) cot x
(b) sin x
(c) cos x
(d) cosec x
Solution:
(b) sin x

(B) Very Short Type Questions With Answers

Question 1.
Write the order of the differential equation whose solution is given by
y = (c₁ + c₂) cos (x + c₃) + c₄\(e^{x+c_5}\) where c₁, c₂, c₄ and c₅ are arbitrary constants.
Solution:
y = (c₁ + c₂) cos (x + c₃) + c₄\(e^{x+c_5}\)
y = (c₁ + c₂) cos (x + c₃) + c₄\(e^{c_5}\).e^x
= A cos(x + c₃) + Be^x
Where c₁ + c₂ = A, c₄\(e^{c_5}\) = B
As there are 3 independent constants the order of the differential equation is 3.

Question 2.
If p and q are respectively degree and order of the differential equation y = e^dy/dx, then write the relation between p and q.
Solution:
Given differential equation is
y = \(e^{\frac{d y}{d x}}\) ⇒ \(\frac{d y}{d x}\) = ln y
Whose order = 1 = p
Degree = 1 = q
∴ p = q

Question 3.
Write the value of \(\int_0^1\){x} dx where {x} stands for fractional part of x.
Solution:

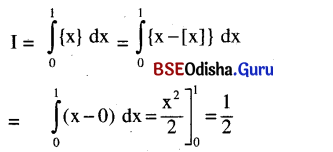
Question 4.
Write the order of the differential equation of the family of circles
ar² + ay² + 2gx + 2fy + c = 0
ax² + ay² + 2gx + 2fy + c = 0
Solution:
As there are 3 independent constants, the order of the differential equation is 3.

Question 5.
If p and q are the order and degree of the differential equation
y\(\left(\frac{d y}{d x}\right)^2\) + x² \(\frac{d^2 y}{d x^2}\) + xy = sin x, then choose the correct statement out of (i) p > q, (ii) p = q, (iii) p < q.
Solution:
Order of the given differential = p = 2
Degree of the given differential equation = q = 1
∴ p > q

Question 6.
Write the order of the differential equation of the system of ellipses:
\(\frac{x^2}{a^2}\) + \(\frac{y^2}{b^2}\) = 1
Solution:
As there are two unknown constants in the system of ellipses \(\frac{x^2}{a^2}\) + \(\frac{y^2}{b^2}\) = 1 the order of the differential equation is 2.

Question 7.
What do you mean by integration? Write your answer in one sentence.
Solution:
Integration is the antiderivative of a function.

Question 8.
Write the differential equation of the family of straight lines parallel to the y-axis.
Solution:
\(\frac{d x}{d y}\) = 0 is the differential equation of family of lines parallel to y-axis.

Question 9.
Write the value of ∫\(\int_{-\pi / 4}^{\pi / 4}\)sin⁵ x cos x dx.
Solution:
Let f(x) = sin⁵ x cos x
f(-x) = sin⁵ (-x) cos (-x)
= -sin⁵ x cos x = -f(x)
i.e. f is an odd function.
Thus \(\int_{-\pi / 4}^{\pi / 4}\)sin⁵ x cos x dx = 0

Question 10.
Write the degree of the differential equation ln\(\left(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\right)\) = y
Solution:
The degree of the differential equation ln\(\left(\frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}\right)\) = y is 1.

Question 11.
What is F'(t) if F(t) = \(\int_a^t\)e^3x .cos 2x dx ?
Solution:
F(t) = \(\int_a^t\)e^3x .cos 2x dx
⇒ F'(t) = e^3x cos 2t

Question 12.
Write the order and degree of the following differential equation:
\(\frac{d^2 y}{d x^2}\) = \(\frac{2 y^3+\left(\frac{d y}{d x}\right)^4}{\sqrt{\frac{d^2 y}{d x^2}}}\)
Solution:
Order = 2, Degree = 3

Question 13.
∫\(\frac{\cot x d x}{\ln \sin x}\) = ?
Solution:
∫\(\frac{\cot x d x}{\ln \sin x}\) = ln(ln sin x) + C

Question 14.
What is F'(x) if F(x) = \(\int_0^{\mathbf{x}}\)e^2t sin 3t dt?
Solution:
If F(x) = \(\int_0^{\mathbf{x}}\)e^2t sin 3t dt then F'(x) = e^2x sin 3x

Question 15.
∫\(\frac{d x}{\cos ^2 x \sin ^2 x}\) = ?
Solution:
∫\(\frac{d x}{\cos ^2 x \sin ^2 x}\) = 4∫\(\frac{d x}{\sin ^2 2 x}\)
= 4∫cosec² 2x dx = -2 cot 2x + C

Question 16.
What is the value of ∫\(\frac{d}{d x}\)f(x) dx – \(\frac{d}{d x}\)(∫f(x) dx)?
Solution:
∫\(\frac{d}{d x}\)f(x) dx – \(\frac{d}{d x}\)(∫f(x) dx)
= f(x) + C – f(x) = C (constant)

Question 17.
If \(\int_1^2\)f(x) dx = λ, then what is the value \(\int_1^2\)f(3 – x) dx?
Solution:
If \(\int_1^2\)f(x) dx = λ, then \(\int_1^2\)f(3 – x) dx = λ

Question 18.
What is the value of \(\int_{-1}^1 \frac{d x}{1+x^2}\)?
Solution:
\(\int_{-1}^1 \frac{d x}{1+x^2}\) = \(\left[\tan ^{-1} x\right]_{-1}^1\)
= tan^-1 1 – tan^-1 (-1)
= tan^-1 1 + tan^-1 1
= 2tan^-1 (1) = 2 . \(\frac{\pi}{4}\) = \(\frac{\pi}{2}\)

Question 19.
Write the order and the degree of the following differential equation:
\(\frac{d^3 y}{d x^3}\) = \(\left(\frac{d^2 y}{d x^2}\right)^2\) + \(\left(\frac{d y}{d x}\right)^4\) + y
Solution:
Order = 3
Degree = 1

Question 20.
Write the particular solution of \(\frac{d y}{d x}\) = (1 + x)⁴, y = 0 when x = -1.
Solution:
\(\frac{d y}{d x}\) = (1 + x)⁴ ⇒ \(\frac{(1+x)^5}{5}\) + C
Given y = 0 for x = -1
⇒ o = o + c ⇒ c = o
∴ The particular solution is y = \(\frac{(1+x)^5}{5}\)

(C) Short Type Questions With Answers

Question 1.
Evaluate: ∫\(\frac{2 x+1}{\sqrt{x^2+10 x+29}}\)dx
Solution:

Question 2.
Evaluate: \(\int_0^{\pi / 2} \frac{\cos x d x}{(2-\sin x)(3+\sin x)}\)
Solution:

Question 3.
Evaluate: ∫\(\frac{d x}{(1+x) \sqrt{1-x^2}}\)
Solution:

Question 4.
Solve: cosec x \(\frac{d^2 y}{d x^2}\) = x.
Solution:
cosec x \(\frac{d^2 y}{d x^2}\) = x => \(\frac{d^2 y}{d x^2}\) = x sin x
⇒ \(\frac{d y}{d x}\) = ∫x sin x dx + A
= x (-cos x) – ∫(-cos x) dx + A
= -x cos x + sin x + A
⇒ y = -∫x cos x dx + ∫sin x dx + A∫dx + B
= [x sin x – ∫sin x dx] – cos x + Ax = B
⇒ y = -x sin x – 2 cos x + Ax + B is the solution.

Question 5.
Find the particular solution of the following differential equation:
\(\frac{d y}{d x}\) = \(\frac{1+y^2}{1+x^2}\) given that y = √3 when x = 1
Solution:

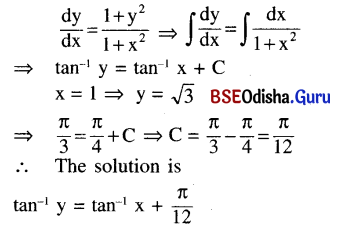
Question 6.
Evaluate: \(\int_0^a x^2\left(a^2-x^2\right)^{5 / 2}\) dx
Solution:

Question 7.
Evaluate: \(\int_0^a \frac{d x}{e^{4 x}-5}\)
Solution:

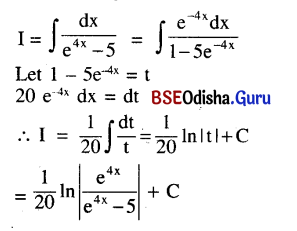
Question 8.
Evaluate: ∫x² tan^-1 x dx.
Solution:

Question 9.
If f(x) = e^x + \(\frac{1}{1+x^2}\) and f(0) = 1, then find f(x).
Solution:
f(x) = e^x + \(\frac{1}{1+x^2}\)
⇒ f(x) = ∫\(\left(e^x+\frac{1}{1+x^2}\right)\)dx + C
= e^x + tan^-1 x + C
f(0) = 1
⇒ 1 = 1 + 0 + C => C = 0
Thus f(x) = e^x + tan^-1 x

Question 10.
Evaluate: ∫(log x)² dx
Solution:
I = ∫(log x)² dx
= (log x)². x – 2∫(log x) . \(\frac{1}{x}\) . x . dx
= x (log x)² – 2 ∫log x. dx
= x (log x)² – 2 {(log x) x – ∫dx}
= x (log x)² – 2x log x + 2x + C

Question 11.
Evaluate: ∫\(\frac{2 x+9}{(x+3)^2}\)dx
Solution:

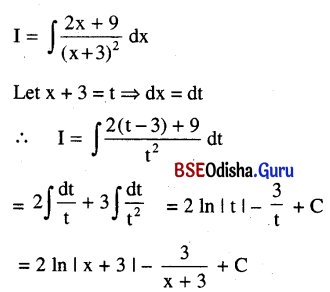
Question 12.
Solve: ydy + e^-y x sin x dx = 0
Solution:
ydy = e^-y x sin x dx = 0
⇒ y e^y dy + x sin x dx = 0
⇒ ∫y e^y dy + ∫x sin x dx =C
⇒ y e^y – e^y + (-x cos x) + sin x = C
⇒ e^y (y – 1) – x cos x + sin x = C is the general solution.

Question 13.
Evaluate: ∫\(\frac{d x}{x \ln x \sqrt{(\ln x)^2-4}}\)
Solution:

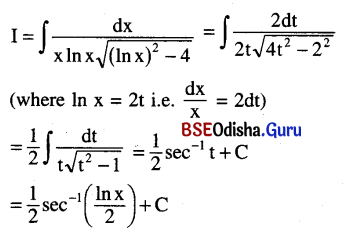
Question 14.
Find the particular solution of the differential equation \(\frac{d^2 y}{d x^2}\) = 6x given that y = 1 and \(\frac{d y}{d x}\) = 2 when x = 0.
Solution:
\(\frac{d^2 y}{d x^2}\) = 6x ⇒ \(\frac{d y}{d x}\) = 6 . \(\frac{x^2}{2}\) + A
\(\frac{d y}{d x}\) = 3x² + A ⇒ y = x³ + Ax + B
Using the givne conditions x = 0, \(\frac{d y}{d x}\) = 2, y = 1, we get
2 = 0 + A ⇒ A = 2
and 1 = 0 + 0 + B ⇒ B = 1
The particular solution is y = x³ + 2x + 1

Question 15.
Evaluate: \(\int_0^{\frac{3}{2}}\)[x²] dx
Solution:

Question 16.
Find the differential equation whose general solution is ax² + by = 1, where a and b are arbitrary constants.
Solution:

Question 17.
Integrate: ∫\(\frac{\sin 6 x+\sin 4 x}{\cos 6 x+\cos 4 x}\) dx.
Solution: