Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 11 Differential Equations Ex 11(c) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 11 Differential Equations Exercise 11(c)
Find the solutions of the following differential equations:
Question 1.
(x + y) dy + (x – y) dx = 0
Solution:
Given equation can be written as
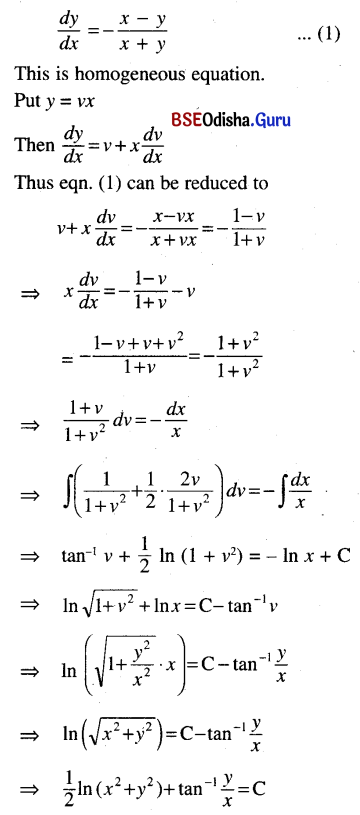
Question 2.
\(\frac{d y}{d x}\) = \(\frac{1}{2}\left(\frac{y}{x}+\frac{y^2}{x^2}\right)\)
Solution:

![]()
Question 3.
(x2 – y2) dx + 2xy dy = 0
Solution:
Given equation can be written as

Question 4.
x\(\frac{d y}{d x}\) + \(\sqrt{x^2+y^2}\) = y
Solution:
Given equation can be written as

Question 5.
x (x + y) dy = (x2 + y2) dx
Solution:

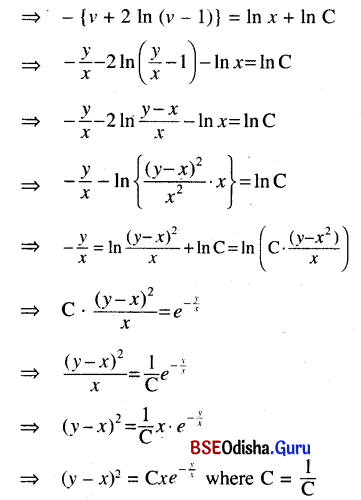
This is the required solution.
![]()
Question 6.
y2 + x2 \(\frac{d y}{d x}\) = xy \(\frac{d y}{d x}\)
Solution:
Given equation can be written as

This is the required solution.
Question 7.
x sin\(\frac{y}{x}\) dy = \(\left(y \sin \frac{y}{x}-x\right)\)dx
Solution:
Given equation can be written as

Question 8.
x dy – y dx= \(\sqrt{x^2+y^2}\) dx
Solution:

This is the required solution.
![]()
Question 9.
\(\frac{d y}{d x}\) = \(\frac{y-x+1}{y+x+5}\)
Solution:
Given equation is


This is the required solution.
Question 10.
(x – y) dy = (x + y + 1) dx
Solution:
Given equation can be written as
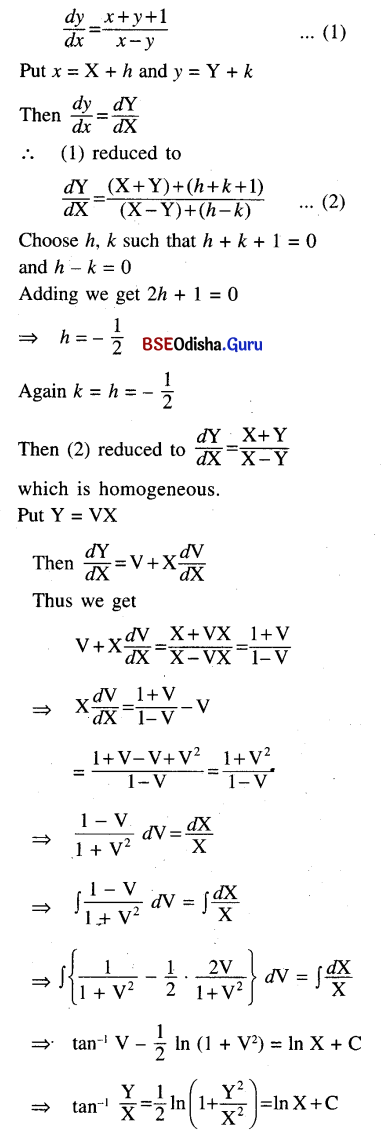

This is the required solution.
Question 11.
(x – y – 2) dx + (x – 2y – 3) dy = 0
Solution:
Given equation can be written as
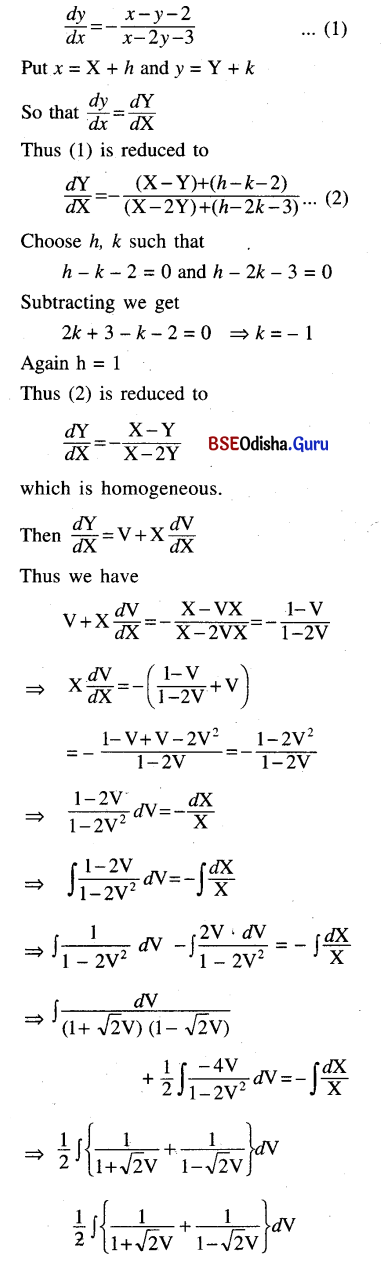
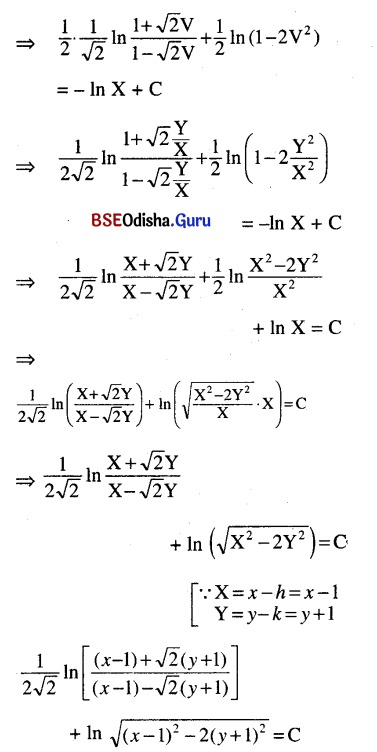
This is the required solution.
![]()
Question 12.
\(\frac{d y}{d x}\) = \(\frac{3 x-7 y+7}{3 y-7 x-3}\)
Solution:
Given equation can be written as

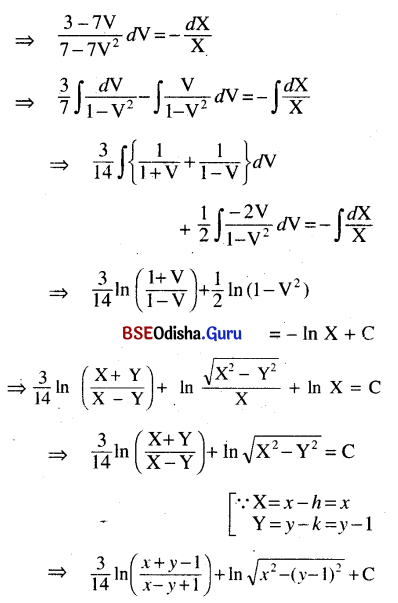
This is the required solution.
Question 13.
(2x + y + 1) dx + (4x + 2y – 1) dy = 0
Solution:
Given equation can be written as

⇒ 2z + ln (z – 1) = 3x + C
⇒ 2 (2x + y) + ln (2x + y – 1 ) = 3x + C
⇒ (x + 2y) + ln (2x + y – 1 ) = C
This is the required solution.
Question 14.
(2x + 3y – 5)\(\frac{d y}{d x}\) + 3x + 2y – 5 = 0
Solution:
Given equation can be written as
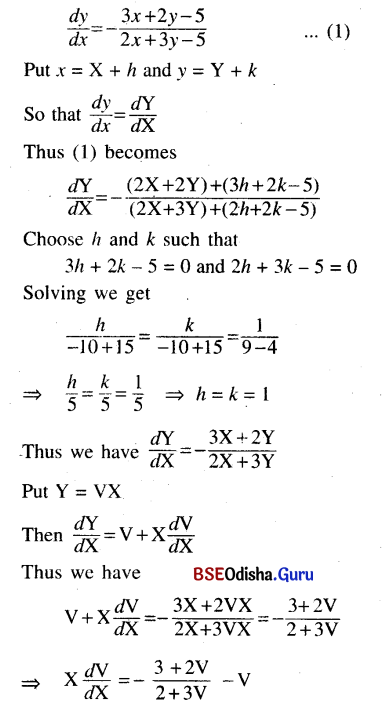
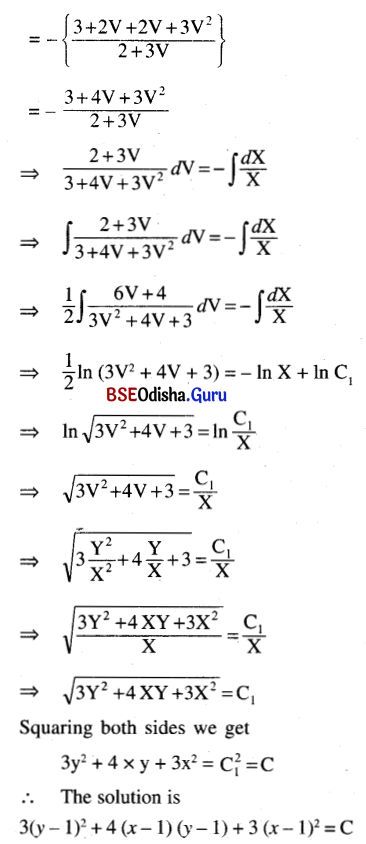
![]()
Question 15.
(4x + 6y + 5) dx – (2x + 3y + 4) dy = 0
Solution:
Given equation can be written as


This is the required solution.
