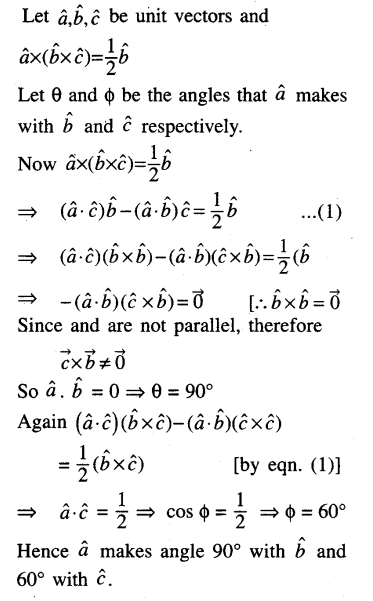CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Ex 12(d)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Ex 12(d) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Exercise 12(d)

Question 1.
Each question given below has four possible answers out of which only one is correct. Choose the correct one.
(i) \(\vec{a} \cdot \vec{b} \times \vec{a}\) = _______.
(a) \(\overrightarrow{0}\)
(b) 0
(c) 1
(d) \(\vec{a}^2 \vec{b}\)
Solution:
\(\vec{a} \cdot(\vec{b} \times \vec{a})\) = \((\vec{b} \times \vec{a}) \cdot \vec{a}\)
= \(\vec{b} \cdot(\vec{a} \times \vec{a})\) = \(\vec{b} \cdot \overrightarrow{0}\)
= 0 [∴ Dot product is commutative and in the scalar triple product the dot and cross can be interchanged.]

(ii) \((-\vec{a}) \cdot \vec{b} \times(-\vec{c}))\) = _______.
(a) \(\vec{a} \times \vec{b} \cdot \vec{c}\)
(b) \(-\vec{a} \cdot(\vec{b} \times \vec{c})\)
(c) \(\vec{a} \times \vec{c} \cdot \vec{b}\)
(d) \(\vec{a} \cdot(\vec{c} \times \vec{b})\)
Solution:
\((-\vec{a}) \cdot \vec{b} \times(-\vec{c})\) = \(\vec{a} \cdot(\vec{b} \times \vec{c})\)

(iii) For the non-zero vectors \(\vec{a}, \vec{b}\) and \(\vec{c}, \vec{a} \cdot(\vec{b} \times \vec{c})\) = 0 if
(a) \(\vec{b} \perp \vec{c}\)
(b) \(\vec{a} \perp \vec{b}\)
(c) \(\vec{a} \| \vec{c}\)
(d) \(\vec{a} \perp \vec{c}\)
Solution:
\(\vec{a} \cdot(\vec{b} \times \vec{c})\) = \((\vec{a} \times \vec{b}) \cdot \vec{c}\)
\(\vec{c} \perp(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}})\)
but \(\vec{a} \times \vec{b}\) is perpendicular to \(\vec{a}\) and \(\vec{b}\)
∴ \(\vec{a} \| \vec{b}\)

Question 2.
Find the scalar triple product \(\vec{b} \cdot(\vec{c} \times \vec{a})\) where \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are respectively.
(i) î + ĵ, î – ĵ, 5î + 2ĵ + 3k̂
Solution:

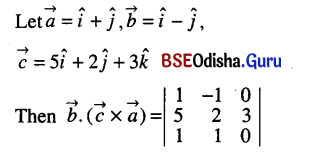
= 1 (0 – 3) + 1 (0 – 3) + 0 (5 – 2)
= 3 – 3 = -6

(ii) 5î – ĵ + 4k̂, 2î + 3ĵ + 5k̂, 5î – 2ĵ
Solution:

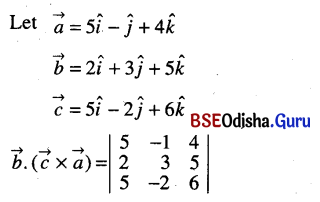
= 5 (18 + 10) + 1 (12 – 25) + 4 (- 4 – 15)
= 140 – 13 – 76 = 140 – 89 = 51

Question 3.
Find the volume of the parallelopiped whose sides are given by the vectors.
(i) î + ĵ + k̂, k̂, 3î – ĵ + 2k̂
Solution:

= 1 (0 + 1) – 1 (0 – 3) + 1 (0 – 0)
= 1 + 3 = 4 cube units.

(ii) (1, 0, 0), (0, 1, 0), (0, 0, 1).
Solution:

Question 4.
Show that the following vector are co-planar
(i) î – 2ĵ + 2k̂, 3î + 4ĵ + 5k̂, -2î + 4ĵ – 4k̂
Solution:

(ii) î + 2ĵ + 3k̂, -2î – 4ĵ + 5k̂, 3î + 6
Solution:

Question 5.
Find the value of λ so that the three vectors are co-planar.
(i) î + 2ĵ + 3k̂, 4î + ĵ + λk̂ and λî – 4ĵ + k̂
Solution:

(ii) (2, -1, 1), (1, 2, -3) and (3, λ, 5)
Solution:

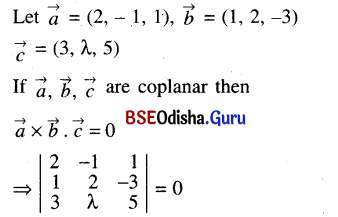
⇒ 2 (10 + 3λ) + 1 (5 + 9) + 1 (λ – 6) = 0
⇒ 20 + 6λ +14 + λ – 6 = 0
⇒ 7λ + 28 = 0 ⇒ λ = -4

Question 6.
If \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) mutually perpendiculars, show that \([\vec{a} .(\vec{b} \times \vec{c})]^2\) = a²b²c²
Solution:

Question 7.
Show that \([\vec{a}+\vec{b} \vec{b}+\vec{c} \vec{c}+\vec{a}]\) = 2\([\vec{a} \vec{b} \vec{c}]\)
Solution:

Question 8.
Prove that \([\vec{a} \times \vec{b} \vec{b} \times \vec{c} \vec{c} \times \vec{a}]\) = \([\vec{a} \vec{b} \vec{c}]^2\)
Solution:

Question 9.
For \(\vec{a}\) = î + ĵ, \(\vec{b}\) = -î + 2k̂, \(\vec{c}\) = ĵ + k̂ obtain \(\vec{a} \times(\vec{b} \times \vec{c})\) and also verify the formula \(\vec{a} \times(\vec{b} \times \vec{c})\) = \((\vec{a} \cdot \vec{c}) \vec{b}-(\vec{a} \cdot \vec{b}) \vec{c}\).
Solution:

Question 10.
Prove that \(\vec{a} \times(\vec{b} \times \vec{c})+\vec{b} \times(\vec{c} \times \vec{a})+\vec{c} \times(\vec{a} \times \vec{b})\) and hence prove that \(\vec{a} \times(\vec{b} \times \vec{c}), \vec{b} \times(\vec{c} \times \vec{a}), \vec{c} \times(\vec{a} \times \vec{b})\) are coplanar.
Solution:

Question 11.
If \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) unit vectors and \(\hat{a} \times(\hat{b} \times \hat{c})=\frac{1}{2} \hat{b}\) find the angles that â makes with b̂ and ĉ, where b̂, ĉ are not parallel.
Solution: