CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(a)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Exercise 3(a)

Question 1.
A merchant sells two models X and Y of TV with cost price ₹25000 and ₹50000 per set respectively. He gets a profit of ₹1500 on model X and ₹2000 on model Y. The sales cannot exceed 20 sets in a month. If he cannot invest more than 6 lakh rupees, formulate the problem of determining the number of sets of each type he must keep in stock for maximum profit.
Solution:
To get maximum profit let x TVs of model X and Y TVs of model Y must be kept in stock.
∴ Total profit = Z = 1500x + 2000y which is to be maximum.
According to the question, the sales cannot exceed 20 sets i.e. x + y ≤ 20.
Again total investment does not exceed 6 lakh.
25000x + 50000y ≤ 600000
⇒ x + 2y ≤ 24
∴ The LPP is:
maximise: Z = 1500x + 2000y
subject to: x + y ≤ 20
x + 2y ≤ 24
x, y ≥ 0

Question 2.
A company manufactures and sells two models of lamps L₁ and L₂, the profit being ₹15 and ₹10 respectively. The process involves two workers W, and W2 who are available for this kind of work 100 hours and 80 hours per month respectively, W1 assembles L₁ in 20 and L₂ in 30 minutes. W2 paints L₁ in 20 and L₂ in 10 minutes. Assuming that all lamps made can be sold, formulate the LPP for determining the production figures for maximum profit.
Solution:
Let x units of L₁ and y units of L₂: are to be produced to get maximum profit.
Total profit = Z = 15x + 10y
According to the question
20x + 30y ≤ 600
and 20x + 10y ≤ 480
=> 2x + 3y ≤ 600
2x + y ≤ 480
.-. The LPP is maximize: Z = 15x + 10y
subject to: 2x + 3y ≤ 600
2x + y ≤ 480
x, y ≥ 0.

Question 3.
A factory uses three different resources for the manufacture of two different products, 20 units of the resource A, 12 units of B and 16 units of C being available. One unit of the first product requires 2, 2 and 4 units of the resources and one unit of the second product requires 4, 2 and 0 units of the resources taken in order. It is known that the first product gives a profit of ₹20 per unit and the second ₹30 per unit. Formulate the LPP so as to earn maximum profit.
Solution:
Let to earn maximum profit the factory produces x units of first product and y units of the second product.
The given data can be summarised as below:

	Resource A	Resource B	Resource C	Profit per unit in ₹
Product – I	2	2	4	20
Product – II	4	2	0	30
Availability	20	12	16

Total profit = 20x + 30y
which is to be maximum.
According to the question
2x + 4y ≤ 20
2x + 2y ≤ 12
4x + 0y ≤ 16
.-. The LPP is
maximize: Z = 20x + 30y
subject to: x + 2y ≤ 10
x + y ≤ 6
x ≤ 4
x, y ≥ 0.

Question 4.
A man plans to start a poultry farm by investing at most ₹3000. He can buy old hens for ₹80 each and young ones for ₹140 each, but he cannot house more than 30 hens. Old hens lay 4 eggs per week and young ones lay 5 eggs per week, each egg being sold at ₹5. It costs ₹5 to feed an old hen and ₹8 to feed a young hen per week. Formulate his problem determining the number of hens of each type he should buy so as to earn a profit of more than ₹300 per week.
Solution:
Let to get maximum profit he has to purchase x old hens and y young hens.
Total cost = 80x + 140y ≤ 3000
⇒ 4x + 7y ≤ 150
Total number of hens x + y ≤ 30
Number of eggs per week = 4x + 5y
Total income per week = 20x + 25y
Total cost to feed per week = 5x + 8y
∴ Weekly profit = 15x + 17y
∴ 15x + 17y > 300
and also total profit = z = 15x + 17y is to be maximum.
∴ The LPP is
maximize: Z = 15x + 17y
subject to: 4x + 7y ≤ 150
x + y ≤ 30
15x + 17y ≥ 300
x, y ≥ 0.

Question 5.
An agro-based company produces tomato sauce and tomato jelly. The quantity of material, machine hour, labour (man-hour) required to produce one unit of each product and the availability of raw material ore given in the following table:

	Sauce	Jelly	availability
Man-hour	3	2	10
Machine hour	1	2.5	7.5
Raw material	1	1.2	4.2

Assume that one unit of sauce and one unit of jelly each yield a profit of ₹2 and ₹4 respectively. Formulate the LPP so as to yield maximum profit.
Solution:
Let the company produces x units of sauce and y units of jelly.
Total profit = 2x + 4y to be maximum.
Man hour = 3x + 2y ≤ 10
Machine hour = x + 2.5y ≤ 7.5
⇒ 2x + 5y ≤ 15
Raw material = x + 1.2y ≤ 4.2
⇒ 5x + 6y ≤ 21
∴ The LPP is
maximize: Z = 2x + 4y
subject to: 3x + 2y ≤ 10
2x + 5y ≤ 15
5x + 6y ≤ 21
x, y ≥ 0.

Question 6.
(Allocation Problem.) A farmer has 5 acres of land on which he wishes to grow two crops X and Y. He has to use 4 cart loads and 2 cartloads of manure per acre for crops X and Y respectively. But not more than 18 cartloads of manure is available. Other expenses are ₹200 and ₹500 per acre for the crops X and Y respectively. He estimates profit from crops X and Y at the rates ₹1000 and ₹800 per acre respectively. Formulate the LPP as to how much land he should allocate to each crop for maximum profit.
Solution:
Let x acres are allocated for crop X and y acres for crop Y.
Total profit = 100x + 800y to be maximum.
According to the question
x + y ≤ 5
Manure = 4x + 2y ≤ 1 8 ⇒ 2x + y ≤ 9
∴ The LPP is
maximize: Z = 1000x + 800y
subject to: x + y ≤ 5
2x + y ≤ 9
x, y ≥ 0.

Question 7.
(Transportation Problem) A company has two factories at locations X and Y. He has to deliver the products from these factories to depots located at three places A, B and C. The production capacities at X and Y are respectively 12 and 10 units and the requirements at the depots are 8, 8 and 6 units respectively. The cost of transportation from the factories to the depots per unit of the product is given below.

(Cost in ₹)
	To →	A	B	C
From	X	210	160	250
	Y	170	180	140

The company has to determine how many units of product should be transported from each factory to each depot so that the cost of transportation is minimum. Formulate this LPP.
Solution:
Let x units are transported from X to A and y units from X to B. The transportation matrix is

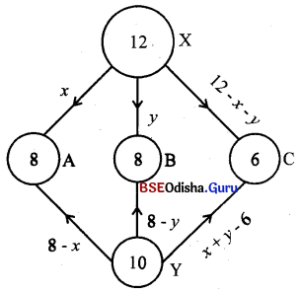
Total cost of transportation
= 210x + 160y + 250 (12 – x – y) +170 (8 – x) +180 (8 – y) + 140 (x + y – 6)
= 4960 – 70x – 130y to be minimum.
Now all costs of transportation are ≥ 0.
∴ x ≥ 0, y ≥ 0.
12 – x – y ≥ 0 ⇒ x + y ≤ 12
8 – x ≥ 0 ⇒ x ≤ 8
8 – y ≥ 0 ⇒ y ≤ 8
x + y – 6 ≥ 0 x + y ≥ 6
∴ The LPP is
Minimize: Z = 4960 – 70x – 130y
subject to: x + y ≤ 12
x ≤ 8
y ≤ 8
x + y ≥ 6
x, y ≥ 0

Question 8.
(Diet Problem) Two types of food X and Y are mixed to prepare a mixture in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. These vitamins are available in one kg of food as per the table given below.

	Vitamins
food	A	B	C
X	1	2	3
Y	2	2	1

One kg. of food X cost ₹16 and one kg. of food Y costs ₹20. Formulate the LPP so as to determine the least cost of the mixture containing the required amount of vitamins.
Solution:
Let x units of food X and y units of food Y are to be mixed to prepare the mixture.
Cost of the mixture = 16x + 20y to be minimum.
According to the question
Vitamin A content = x + 2y ≥ 10
Vitamin B content = 2x + 2y ≥ 12
Vitamin C content = 3x + y ≥ 8
∴ The LPP is
minimize: Z = 16x + 20y
subject to x + 2y ≥ 10
x + y ≥ 6
3x + y ≥ 8
x, y ≥ 0.

Question 9.
Special purpose coins each weighing 10gms are to be manufactured using two basic metals M₁ and M₂ and a mix of other metals M₃. M₁, M₂ and M₃ cost ₹500, ₹800 and ₹50 per gram respectively. The strength of a coin demands that not more than 7gm. of M₁ and a minimum of 3 gm of M₁ should be used. The amount of M₃ in each coin is maintained at 25% of that of M₁. Since the demand for the coin is related to its price, formulate the LPP to find the minimum cost of a coin.
Solution:
Let x gm of M₁ and y g of M₂ are used to make the coin. According to the demand of the coin \(\frac{x}{4}\) g of M₃ is to be mixed.
Cost of the coin = 500x + 800y + \(\frac{50 x}{4}\)
= (512.5)x + 800y
which is to be minimum.
Again weight of the coin = 10g
⇒ x + y + \(\frac{x}{4}\) = 10
⇒ 5x + 4y = 40
According to the question x ≤ 7, y ≤ 3.
Thus the L.P.P is
minimize: Z = (512.5)x + 800y
subject to: 5x + 4y = 40
x ≤ 7
x ≤ 3
x, y ≥ 0.

Question 10.
A company produces three types of cloth A, B and C. Three kinds of wool, say red, green and blue are required for the cloth. One unit length of type A cloth needs 2 metres of red and 3 metres of blue wool; one unit length of type B cloth needs 3 metres of red, 2 metres of green and 2 metres of blue wool and one unit length of type C cloth needs 5 metres of green and 4 metres of blue wool. The firm has a stock of only 80 metres of red, 100 metres of green and 150 metres of blue wool. Assuming that income obtained from one unit length of cloth is ₹30, ₹50 and ₹40 of types A, B and C respectively, formulate the LPP so as to maximize income.
Solution:
Let x units of cloth A, y units of cloth B and z units of cloth C are to be produced from the available materials to get the maximum income. The given data can be summarised as:

	Red wool	Green wool	Blue wool	Income
Cloth A	2	–	3	30
Cloth B	3	2	2	50
Cloth C	–	5	4	40
Availability	80	100	150

Total Income = 30x + 50y + 40z
which is to be maximum.
According to the question
2x + 3y ≤ 80
2y + 5z ≤ 100
3x + 2y + 4z ≤ 150
Thus the L.P.P. is
minimize: Z = 30x + 50y + 40z
subject to: 2x + 3y ≤ 80
2y + 5z ≤ 100
3x + 2y + 4z ≤ 150
x, y, z ≥ 0

Question 11.
A person wants to decide the constituents of a diet which will fulfil his daily requirements of proteins, fats and carbohydrates at minimum cost. The choice is to be made from three different types of food. The yields per unit of these foods are given in the following table.

food	yield/unit			cost/unit
	Protein	Fat	Carbonate
f1	3	2	6	45
f2	4	2	3	40
f3	8	7	7	85
Minimum Requirement	100	200	800

Formulate the LPP.
Solution:
Let the diet constitues x units of f1, y units of f2 and z units of f3.
Total cost = 45x + 40y + 85z, which is to be minimum.
According to the question
3x + 4y + 8z ≥ 1000
2x + 2y + 7z ≥ 200
6x + 3y + 7z ≥ 800
Thus the LPP is
Minimize: Z = 45x + 40y + 85z
Subject to: 3x + 4y + 8z ≥ 1000
2x-+2y + 7z ≥ 200
6x + 3y + 7z ≥ 800
x, y, z ≥ 0