CHSE Odisha Class 12 Math Solutions Chapter 4 Matrices Ex 4(b)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 4 Matrices Ex 4(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 4 Matrices Exercise 4(b)

Question 1.
State which of the following matrices are symmetric, skew-symmetric, both or not either:

Solution:
(i) Symmetric
(ii) Neither Symmetric nor skew-symmetric
(iii) Symmetric
(iv) Skew symmetric
(v) Both
(vi) Neither symmetric nor skew-symmetric
(vii) Skew symmetric

Question 2.
State ‘True’ or ‘False’:
(i) If A and B are symmetric matrices of the same order and AB – BA ≠ 0, then AB is not symmetric.
Solution:
True

(ii) For any square matrix A, AA’ is symmetric.
Solution:
True

(iii) If A is any skew-symmetric matrix, then A² is also skew-symmetric.
Solution:
False

(iv) If A is symmetric, then A², A³, …, Aⁿ are all symmetric.
Solution:
True

(v) If A is symmetric then A – A¹ is both symmetric and skew-symmetric.
Solution:
False

(vi) For any square matrix (A – A¹)² is skew-symmetric.
Solution:
True

(vii) A matrix which is not symmetric is skew-symmetric.
Solution:
False

Question 3.
(i) If A and B are symmetric matrices of the same order with AB ≠ BA, final whether AB – BA is symmetric or skew symmetric.
Solution:
A and B are symmetric matrices;
Thus A’ = A and B’ = B
Now (AB – BA)’ = (AB)’ – (BA)’
= B’A’ – A’B’
= BA – AB = – (AB – BA)
∴ AB – BA is skew symmetric.

(ii) If a symmetric/skew-symmetric matrix is expressed as a sum of a symmetric and a skew-symmetric matrix then prove that one of the matrices in the sum must be zero matrix.
Solution:
We know that zero matrix is both symmetric as well as skew-symmetric.
Let A is symmetric.
∴ A = A + O where A is symmetric and O is treated as skew-symmetric. If B is skew-symmetric then we can write B = O + B where O is symmetric and B is skew-symmetric.

Question 4.
A and B are square matrices of the same order, prove that
(i) If A, B and AB are all symmetric, then AB – BA = 0
Solution:
Let A, B and AB are all symmetric.
∴A’ = A, B’ = B and (AB)’ = AB
⇒ B’A’ = AB
⇒ BA = AB
⇒ AB – BA = 0

(ii) If A, B and AB are all skew symmetric then AB + BA = 0
Solution:
Let A, B and AB are all skew symmetric matrices
∴ A’ = -A, B’ = -B and (AB)’ = -AB
Now (AB)’ = -AB
⇒ B’A’ = -AB
⇒ (-B) (-A) = -AB
⇒ BA = -AB
⇒ AB + BA = 0

Question 5.
If A = \(\left[\begin{array}{rrr}
1 & 2 & 0 \\
0 & 1 & 3 \\
-2 & 5 & 3
\end{array}\right]\), then verify that A’ = \(\left[\begin{array}{ccc}
1 & 0 & -2 \\
2 & 1 & 5 \\
0 & 3 & 3
\end{array}\right]\)

(i) A+A’ is symmetric

(ii) A-A’ is skew-symmetric

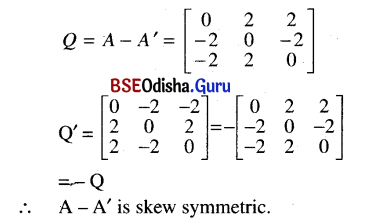
Question 6.
Prove that a unit matrix is its own inverse. Is the converse true?
IfA = \(\left[\begin{array}{rrr}
0 & 1 & -1 \\
4 & -3 & 4 \\
3 & -3 & 4
\end{array}\right]\) show that A² = I and hence A= A^-1.
Solution:
No the converse is not true for example:

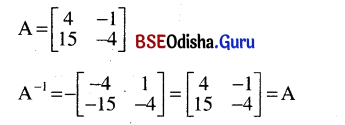
Question 7.
Here A is an involuntary matrix, recall the definition given earlier.
Solution:

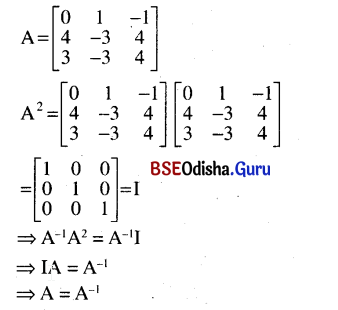
Question 8.
Show that \(\left[\begin{array}{ll}
\mathbf{0} & \mathbf{1} \\
\mathbf{1} & \mathbf{0}
\end{array}\right]\) is its own inverse.
Solution:

Question 9.
Express as a sum of a symmetric and a skew symmetric matrix.

Solutions:

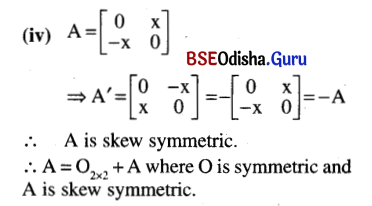
Question 10.
What is the inverse of

Question 11.
Find inverse of the following matrices by elementary row/column operation (transformations):
(i) \(\left[\begin{array}{ll}
1 & 2 \\
3 & 5
\end{array}\right]\)
Solution:

(ii) \(\left[\begin{array}{ll}
2 & 5 \\
1 & 3
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{cc}
4 & -2 \\
3 & 1
\end{array}\right]\)
Solution:

(iv) \(\left[\begin{array}{ll}
2 & 5 \\
1 & 3
\end{array}\right]\)
Solution:

(v) \(\left[\begin{array}{cc}
1 & 0 \\
2 & -3
\end{array}\right]\)
Solution:

(vi) \(\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\)
Solution:

Question 12.
Find the inverse of the following matrices using elementary transformation:
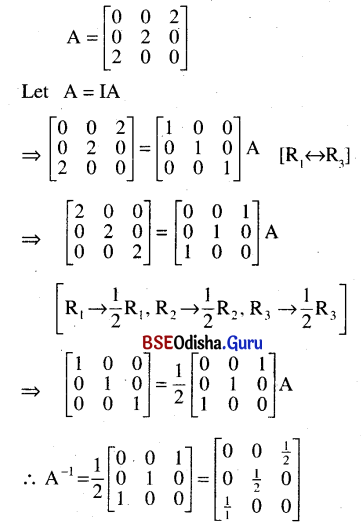
(i) \(\left[\begin{array}{lll}
\mathbf{0} & \mathbf{0} & 2 \\
\mathbf{0} & \mathbf{2} & \mathbf{0} \\
\mathbf{2} & \mathbf{0} & \mathbf{0}
\end{array}\right]\)
Solution:

(ii) \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{ccc}
3 & -2 & 3 \\
2 & 1 & -1 \\
4 & -3 & 2
\end{array}\right]\)
Solution:

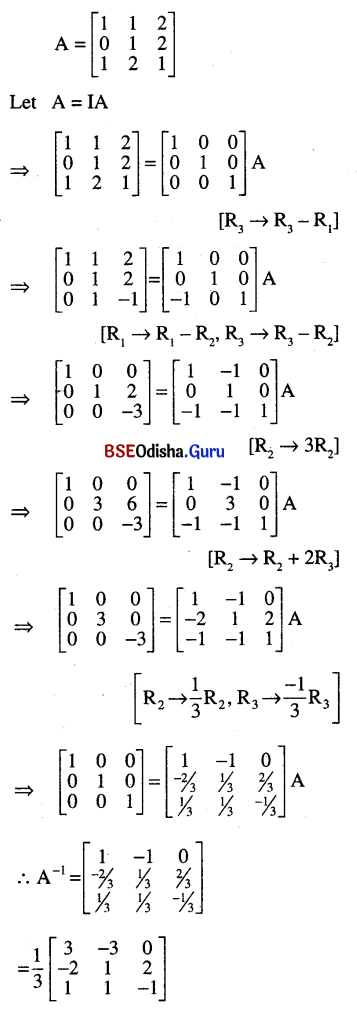
(iv) \(\left[\begin{array}{lll}
1 & 1 & 2 \\
0 & 1 & 2 \\
1 & 2 & 1
\end{array}\right]\)
Solution:

(v) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 1 & 4 \\
1 & 0 & 2
\end{array}\right]\)
Solution: