CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(f)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(f) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(f)

Find the following limits:
Question 1.
\(\lim _{x \rightarrow 0} \frac{\tan a x}{x}\)
Solution:

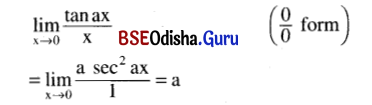
Question 2.
\(\lim _{x \rightarrow 0} \frac{\sin a x}{\sin b x}\)
Solution:

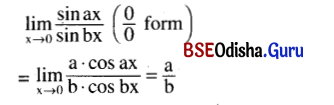
Question 3.
\(\lim _{x \rightarrow 1} \frac{\ln x}{x^2-1}\)
Solution:

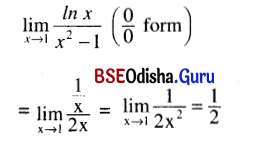
Question 4.
\(\lim _{x \rightarrow \frac{\pi}{2}} \frac{1-\sin x}{\cos x}\)
Solution:

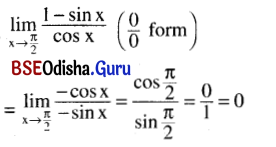
Question 5.
\(\lim _{x \rightarrow 0} \frac{x-\sin x}{\tan ^3 x}\)
Solution:

Question 6.
\(\lim _{x \rightarrow 2} \frac{x^3-12 x+16}{3 x^3-8 x^2-4 x+16}\)
Solution:

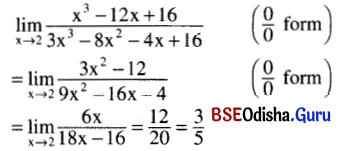
Question 7.
\(\lim _{x \rightarrow 1} \frac{{In}(2-x)}{1-x^2}\)
Solution:

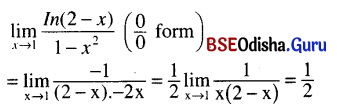
Question 8.
\(\lim _{x \rightarrow 0+} \frac{\sqrt{1-x}-\sqrt{1+x}}{\sqrt{x}}\)
Solution:

Question 9.
\(\lim _{x \rightarrow 1} \frac{2 \sqrt{x}-3 \sqrt[3]{x}+1}{(x-1)^2}\)
Solution:

Question 10.
\(\lim _{x \rightarrow \infty} \frac{x^3-3 x+1}{2 x^3-7 x^2+5}\)
Solution:

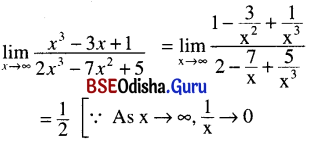
Question 11.
\(\lim _{x \rightarrow 2} \frac{4^x-2^{3+x}+16}{(x-2)^2}\)
Solution:

Question 12.
\(\lim _{x \rightarrow 0+} \frac{\ln \tan x}{\ln \sin 2 x}\)
Solution:

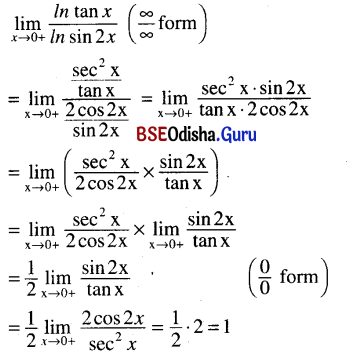
Question 13.
\(\lim _{x \rightarrow 0} \frac{e^x-e^{-x}-2 \sin x}{x \sin x}\)
Solution:

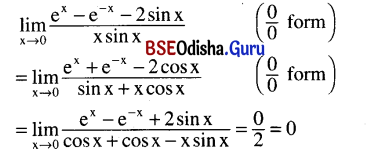
Question 14.
\(\lim _{x \rightarrow \infty} \frac{{In}\left(\frac{1}{x}\right)}{x^x}\)
Solution:

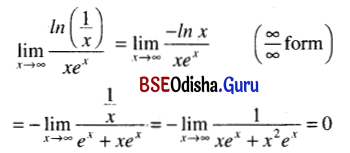
Question 15.
\(\lim _{x \rightarrow 0+} \frac{e^{-\frac{1}{x}}}{x}\)
Solution:

Question 16.
\(\lim _{x \rightarrow \infty} \frac{x^n+x^{-1}}{(x+2)^n}\)
Solution:

Question 17.
\(\lim _{x \rightarrow 0} \frac{e^x-e^{-x}}{x \cos x}\)
Solution:

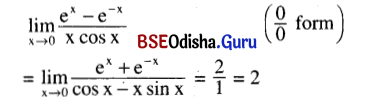
Question 18.
\(\lim _{x \rightarrow \infty} \frac{\sin ^{-1} x}{x}\)
Solution:

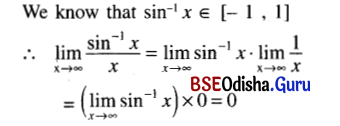
Question 19.
\(\lim _{x \rightarrow 0+}\) log tanx tan 2x
Solution:

Question 20.
\(\lim _{x \rightarrow \pi / 2}\)(tan x)^{cos x}
Solution:

Question 21.
\(\lim _{x \rightarrow 1} x^{\frac{1}{1-x}}\)
Solution:

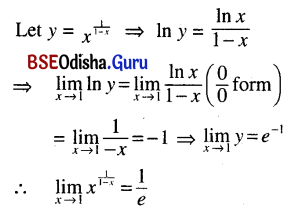
Question 22.
\(\lim _{x \rightarrow 0+} x^{\sin x}\)
Solution:

Question 23.
\(\lim _{x \rightarrow 1}\left(\frac{1}{x-1}-\frac{1}{\ln x}\right)\)
Solution:

Question 24.
\(\lim _{x \rightarrow \infty}\left(x-\sqrt{x^2-1}\right)\)
Solution:

Question 25.
\(\lim _{x \rightarrow \infty}\left(x-\sqrt{x^2+2 x}\right)\)
Solution:

Question 26.
\(\lim _{x \rightarrow 0}\left(\frac{1}{\sin ^2 x}-\frac{1}{x^2}\right)\)
Solution:

Question 27.
\(\lim _{x \rightarrow \pi / 2}\) (tan 3x – tan x)
Solution:

Question 28.
\(\lim _{x \rightarrow 0+} \frac{\sqrt{a^x-b^x}}{\sqrt{x}}\), a > b
Solution:

Question 29.
\(\lim _{x \rightarrow \infty}\left(1+\frac{3}{x}\right)^x\)
Solution:

Question 30.
\(\lim _{x \rightarrow \infty}\left(e^{\frac{1}{x}}\right)^{\ln (1+x)}\)
Solution:

Question 31.
\(\lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^{1 / x}\)
Solution:

Question 32.
\(\lim _{x \rightarrow 0}\left(1+x^2\right)^{1 / x}\)
Solution:

Question 33.
\(\lim _{x \rightarrow 0}\) (cot x – cosec x)
Solution:

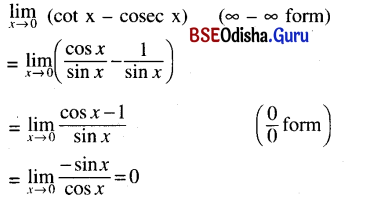
Question 34.
\(\lim _{x \rightarrow 1}\) (2 – x)^{cosec πx}
Solution:

Question 35.
\(\lim _{x \rightarrow 0}\left(\frac{x^2+2 x-1}{x^2-1}\right)^{\frac{1}{x}}\)
Solution:

Question 36.
\(\lim _{x \rightarrow 0} \frac{(1+x)^{1 / x}-e}{x}\)
Solution:

Question 37.
\(\lim _{x \rightarrow 0}(\tan x)^{1 / \ln x}\)
Solution:

Question 38.
\(\lim _{x \rightarrow 0} \frac{x^3 \sin \frac{1}{x}}{\tan x}\)
Solution:

Question 39.
\(\lim _{x \rightarrow 0+} \frac{2^x-1}{\sqrt{(1+x)}-1}\)
Solution:

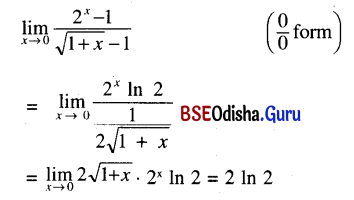
Question 40.
\(\lim _{x \rightarrow 1}(1-x) \tan \frac{\pi x}{2}\)
Solution:

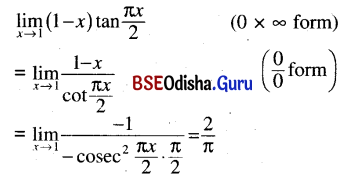
Question 41.
\(\lim _{x \rightarrow 0} \frac{x \cos x-\sin x}{x^2 \sin x}\)
Solution:

Question 42.
\(\lim _{x \rightarrow 0} \frac{e^{-\frac{1}{x^2}}}{x^2}\)
Solution:

Question 43.
\(\lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^{\frac{1}{x^2}}\)
Solution: