CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Ex 9(b)

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(b)

Integrate the following:
(In some cases suggestions have been given for substitution.)
(i) ∫sin 3x dx
Solution:

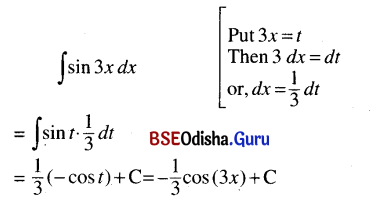
(ii) ∫cos ax dx
Solution:

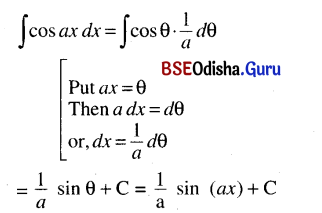
(iii) ∫cos (2 – 7x) dx
Solution:

(iv) ∫sin \(\frac{x}{2}\) dx
Solution:

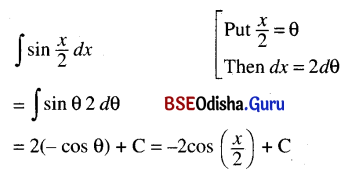
(v) ∫sec² 4x dx
Solution:

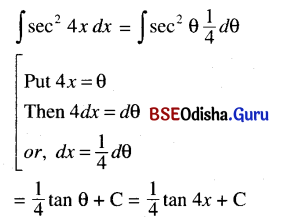
(vi) ∫cosec² \(\frac{x}{3}\) dx
Solution:

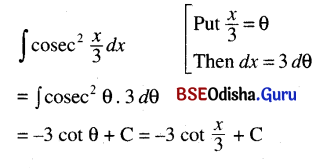
(vii) ∫sec (x + 2) tan (x + 2) dx
Solution:
∫sec (x + 2) tan (x + 2) dx
[Put x + 2 = θ
Then dx = dθ]
= ∫sec θ . tan θ dθ
= sec θ + C = sec (x + 2) + C

(viii) ∫cosec (x + \(\frac{\pi}{4}\)) cot (x + \(\frac{\pi}{4}\)) dx (x + \(\frac{\pi}{4}\) = z)
Solution:

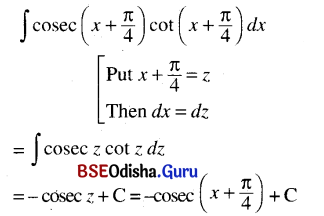
(ix) ∫x² cos x³ dx (x³ = z)
Solution:

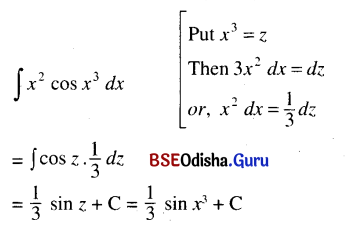
(x) ∫e^x . sec e^x tan e^x dx (e^x = z)
Solution:
∫e^x . sec e^x . tan e^x dx
[Put e^x = z
Then e^x dx = dz]
= ∫ sec z . tan z dz
= sec z + C = sec e^x + C

(xi) ∫\(\frac{\sec ^2 \sqrt{x}}{\sqrt{x}}\) dx
Solution:

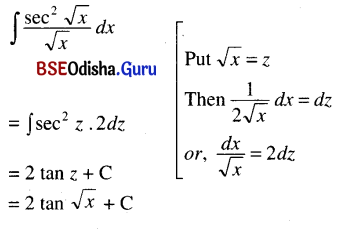
Question 2.
(i) ∫sin x cos x dx (sin x = v)
Solution:
∫sin x cos x dx
[Put sin x = v
Then cos x dx = dv]
= ∫v dv = \(\frac{1}{2}\)v² + C
= \(\frac{1}{2}\)sin² x + C

(ii) ∫tan³ x sec² x dx (tan x = t)
Solution:
∫tan³ x sec² x dx
[Put tan x = t
Then sec² x dx = dt]
= ∫t³ dt = \(\frac{1}{4}\)t⁴ + C
= \(\frac{1}{4}\)tan⁴ x + C

(iii) ∫\(\frac{{cosec}^2 x}{1+\cot x}\) dx
Solution:
∫\(\frac{{cosec}^2 x}{1+\cot x}\) dx
[Put 1 + cot x = t
Then -cosec² x dx = dt
or, cosec² x dx = – dt]
= ∫\(\) = -∫\(\) = -ln |t| + C
= -ln |1 + cot x| + C

(iv) ∫\(\frac{\sin x}{\cos ^3 x}\) dx
Solution:

(v) ∫\(\frac{\cos x}{\sin ^5 x}\) dx
Solution:

(vi) ∫\(\frac{{cosec}^2 x(\ln x)}{x}\) dx (In x = z)
Solution:
∫\(\frac{{cosec}^2 x(\ln x)}{x}\) dx
[Put ln x = z
Then \(\frac{d x}{x}\) = dz]
= ∫cosec² z dz
= -cot z + C = -cot (ln x) + C

(vii) ∫\(\sqrt{1-\sin x}\) cos x dx
Solution:

Question 3.
(i) ∫x\(\sqrt{x^2+3}\) dx (x² + 3 = v)
Solution:

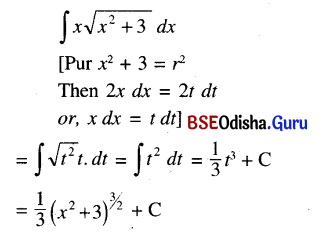
(ii) ∫\(\frac{7 d x}{2-3 x}\) dx
Solution:

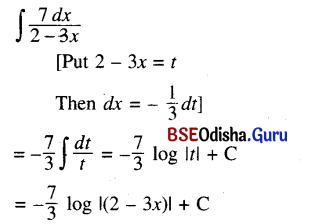
(iii) ∫\(\frac{x}{\sqrt{x^2-a^2}}\) dx
Solution:

(iv) ∫\(\frac{x^2+1}{\left(x^3+3 x+7\right)^3}\) dx
Solution:

(v) ∫(x⁴ – 3x² + 1)⁴ (2x³ – 3x) dx
Solution:

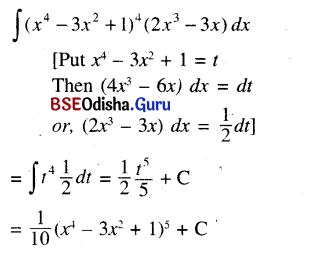
Question 4.
(i) ∫e^3x dx
Solution:
∫e^3x dx
[Put 3x = t
Then 3 dx = dt
or, dx = \(\frac{1}{3}\)dt]
= ∫e^t . \(\frac{1}{3}\)dt = \(\frac{1}{3}\)e^t + C
= \(\frac{1}{3}\)e^3x + C

(ii) ∫e^2x+7 dx
Solution:
∫e^2x+7 dx
[Put 2x + 7 = t
Then 2 dx = dt
or, dx = \(\frac{1}{2}\)dt]
= ∫e^t . \(\frac{1}{2}\)dt = \(\frac{1}{2}\)e^t + C
= \(\frac{1}{2}\)e^2x+7 + C

(iii) ∫e^x/3 dx
Solution:
[Put \(\frac{x}{3}\) = t
Then dx = 3 dt
= ∫e^t . 3dt = 3e^t + C = 3e^x/3 + C

(iv) ∫\(e^{x^3}\) x² dx
Solution:

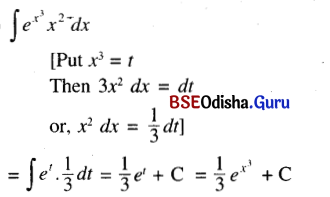
(v) ∫a^2x dx
Solution:

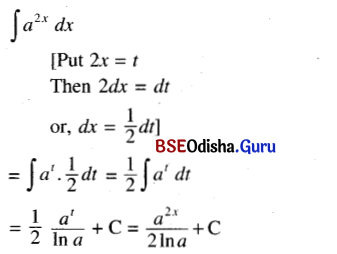
(vi) ∫2\(a^{x^2}\) x dx
Solution:

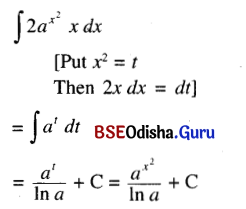
(vii) ∫e^2tanx sec² x dx
Solution:

(viii) ∫\(\frac{e^x}{\left(e^x-2\right)^2}\) dx
Solution:

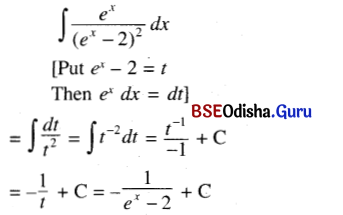
(ix) ∫\(e^{\cos ^2 x}\) sin 2x dx
Solution:
∫\(e^{\cos ^2 x}\) sin 2x dx
[Put cos2 x = t
Then 2cos x (-sin x)dx – dt
or, -sin 2x dx = dt
or, sin 2x dx = -dt]
= ∫e^t (-dt) = e^t + C = –\(e^{\cos ^2 x}\) + C

Question 5.
(i)∫\(\frac{\sin ^{-1} x}{\sqrt{1-x^2}}\) dx
Solution:

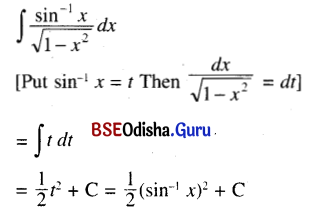
(ii)∫\(\frac{d x}{\sqrt{1-(x-1)^2}}\)
Solution:

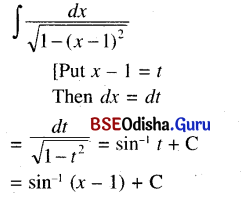
(iii)∫\(\frac{\left(\sec ^{-1} x\right)^2 d x}{x \sqrt{x^2-1}}\)
Solution:

(iv)∫\(\frac{d x}{x\left[1+(\ln x)^2\right]}\)
Solution:

(v)∫\(\frac{d x}{x^2+2 x+2}\) (Integrate \(\frac{d x}{(x+1)^2+1}\))
Solution:

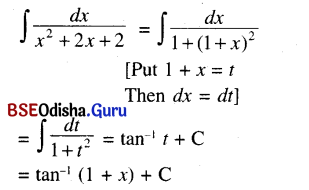
Question 6.
(i) ∫tan 3x dx
Solution:

(ii) ∫cos \(\frac{x}{3}\) dx
Solution:

(iii) ∫sec (2x + 1) dx
Solution:
∫sec (2x + 1) dx
[Put 2x + 1 = t
Then 2 dx = dt
or, dx = \(\frac{1}{2}\)dt]
= ∫sec t . \(\frac{1}{2}\)dt = \(\frac{1}{2}\) ∫sec t dt
= \(\frac{1}{2}\) ln |sec t + tan t| + C
= \(\frac{1}{2}\) ln |sec (2x + 1) + tan (2x + 1)| + C

(iv) ∫cosec 7x dx
Solution:
∫cosec 7x dx
[Put 7x = t
Then 7 dx = dt
or, dx = \(\frac{1}{7}\)dt]
= ∫cosec t . \(\frac{1}{7}\)dt
= \(\frac{1}{7}\) ln |cosec t + cot t| + C
= \(\frac{1}{7}\) ln |cosec 7x + cot x| + C

(v) ∫2x cot (x² + 3) dx    (x² + 3 = z)
Solution:
∫2x cot (x² + 3) dx
[Put x² + 3 = z
Then 2x dx = dz]
= ∫cot dz
= In |sin z| + C
= In |sin (x² + 3)| + C

(vi) ∫e^x tan e^x dx
Solution:
∫e^x tan e^x dx
[Put e^x = t
Then e^x dx = dt]
= ∫tan t dt
= In |sec t| + C
= In |sec e^x| + C

(vii) ∫(sec 2x – 3)² dx
Solution:
∫(sec 2x – 3)² dx
∫sec² 2x dx – 6∫sec 2x dx + 9∫dx
= \(\frac{1}{2}\) tan 2x – 3 ln |sec 2x + tan 2x| + 9x + C

Question 7.
(i) ∫\(\frac{e^x+e^{-x}}{e^x-e^{-x}}\) dx
Solution:
∫\(\frac{e^x+e^{-x}}{e^x-e^{-x}}\) dx
[Put (e^x – e^-x) = t
Then (e^x + e^-x)dx = dt]
= ∫\(\frac{d t}{t}\) = ln |t| + C = ln |(e^x – e^-x| + C

(ii) ∫3^x e^2x dx
Solution:

(iii) ∫\(\frac{(x+1) \ln \left(x^2+2 x+2\right)}{x^2+2 x+2}\) dx
Solution:

Question 8.
(i) ∫\(\frac{\sin x}{\sin (x+\alpha)}\) dx
Solution:

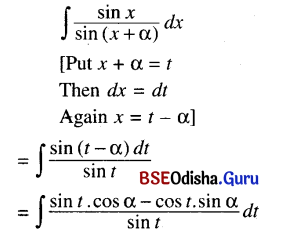
= ∫(cos α – sin α . cot t) dt
= cos α ∫dt – sin α ∫cot dt
= cos α . t – sin α . ln |sin t| + C
= (x + α) cos α – sin α  ln |sin (x + α)| + C
= x cos α – sin α ln |sin (x + α)| + C

(ii) ∫\(\frac{\sin x}{\cos (x-\alpha)}\) dx
Solution:

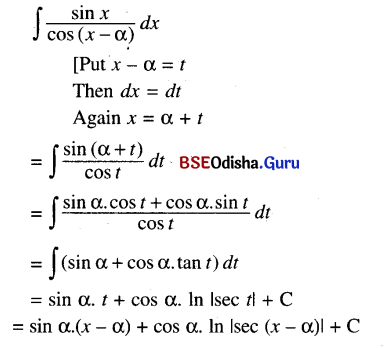
(iii) ∫\(\frac{\tan x+\tan \alpha}{\tan x-\tan \alpha}\) dx
Solution: