Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(h) Textbook Exercise questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(h)
Evaluate the following Integrals.
Question 1.
(i) ∫\(\frac{d x}{4+5 \cos x}\)
Solution:

(ii) ∫\(\frac{d x}{3+\cos x}\)
Solution:

![]()
(iii) ∫\(\frac{d x}{3+\sin x}\)
Solution:

(iv) ∫\(\frac{d x}{1+2 \sin x}\)
Solution:

(v) ∫\(\frac{d x}{2 \sin x+3 \cos x}\)
Solution:

![]()
(vi) ∫\(\frac{d x}{1+\cos x+\sin x}\)
Solution:

Question 2.
(i) ∫\(\frac{3 \sin x+28 \cos x}{5 \sin x+6 \cos x}\) dx
Solution:

(ii) ∫\(\frac{12 \sin x-2 \cos x+3}{\sin x+\cos x}\) dx
Solution:
Let 12 sin x – 2 cos x = A (sin x + cos x) + B ( cos x – sin x)
[Note that cos x – sin x is the derivative of sin x + cos x]
Then A – B = 12, A + B = -2
⇒ 2A = 10
⇒ A = 5, B = -7
Thus 12 sin x – 2 cos x = 5 (sin x + cos x) – 7 (cos x – sin x)
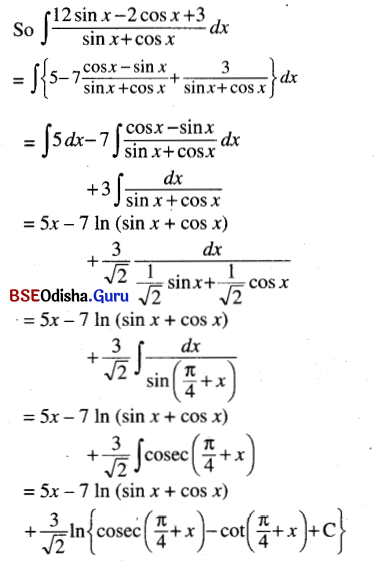
(iii) ∫\(\frac{5 \sin x}{3-2 \sin x}\) dx
Solution:

![]()
(iv) ∫\(\frac{2 \cos x+7}{4-\sin x}\) dx
Solution:


Question 3.
(i) ∫\(\frac{d x}{2 \cos ^2 x+3 \cos x}\)
Solution:
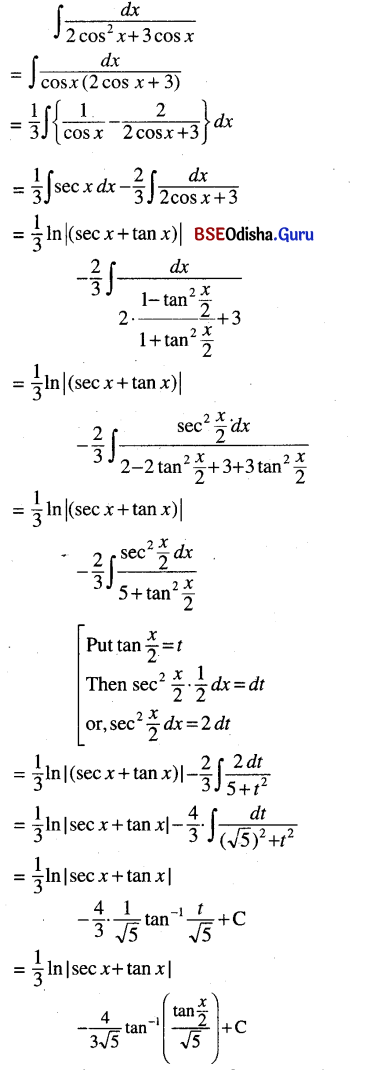
(ii) ∫\(\frac{d x}{4 \sin ^2 x-\sin x}\)
Solution:


![]()
(iii) ∫\(\frac{\sin x \cos x}{x \sin ^2 x-2 \sin x+3}\) dx
Solution:

(iv) ∫\(\frac{d x}{\cos x-\cos 3 x}\)
Solution:
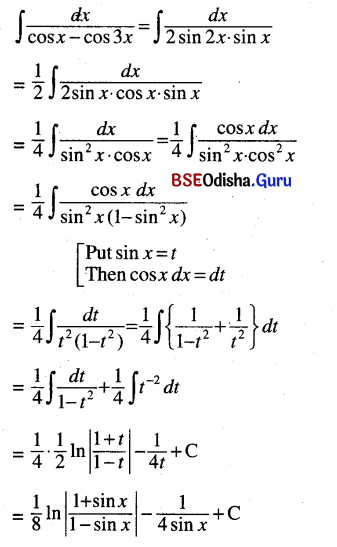
Question 4.
(i) ∫\(\frac{d \theta}{4+3 \sin ^2 \theta}\)
Solution:

(ii) ∫\(\frac{d \theta}{2-3 \cos ^2 \theta}\)
Solution:

(iii) ∫\(\frac{d \theta}{4 \cos ^2 \theta+9 \sin ^2 \theta}\)
Solution:

(iv) ∫\(\frac{d \theta}{2+3 \cos ^2 \theta-4 \sin ^2 \theta}\)
Solution:

Question 5.
(i) ∫\(\frac{\sin 3 x}{\cos 7 x \cos 4 x}\) dx
Solution:
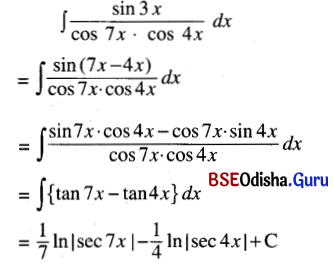
(ii) ∫\(\frac{\cos 2 x}{\sin 7 x \cos 5 x}\) dx
Solution:
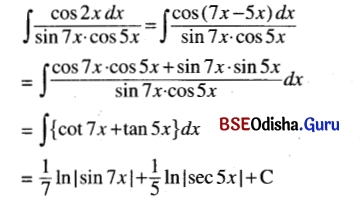
![]()
Question 6.
(i) ∫\(\frac{d x}{\cos x(5+3 \cos x)}\)
Solution:

(ii) ∫\(\frac{d x}{\cos x(1+2 \sin x)}\)
Solution:

