BSE Odisha 10th Class Maths Notes Algebra Chapter 7 ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷା

Odisha State Board BSE Odisha 10th Class Maths Notes Algebra Chapter 7 ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷା will enable students to study smartly.

BSE Odisha Class 10 Maths Notes Algebra Chapter 7 ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷା

→ ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷାରେ ସମାନ୍ତର ପ୍ରଗତିର ପ୍ରୟୋଗ :

→ ଉଦ୍ଦେଶ୍ୟ – ସଡ଼କରେ ଯାତାୟତ କରିବା ସମୟରେ ବିଭିନ୍ନ ଟ୍ରାଫିକ୍ ନିୟମ ଓ ସଂକେତ ସବୁ ମାନିବାକୁ ପଡ଼ିଥାଏ । ଟ୍ରାଫିକ୍ ସଂକେତଗୁଡ଼ିକ ମଧ୍ୟରେ ଥ‌ିବା ଦୂରତା ଓ ସେଗୁଡ଼ିକୁ ଅତିକ୍ରମ କରିବାର ସମୟକୁ ନେଇ ଏକ ସମାନ୍ତର ଅନୁକ୍ରମ (Arithmatic Sequence) ସୃଷ୍ଟି କରି ଏହି ପ୍ରକ୍ରିୟାକୁ ଏକ ଗାଣିତିକ ଭିଭି ଦେବା ଏହି ପାଠ୍ୟର
ଉଦ୍ଦେଶ୍ୟ ଅଟେ ।

→ ପ୍ରସଙ୍ଗ – ଏକ ସମାନ୍ତର ପ୍ରଗତିରେ ସଂଖ୍ୟାଗୁଡ଼ିକର ଅନୁକ୍ରମ ଓ ସେମାନଙ୍କର ସମାନ୍ତର ଶ୍ରେଣୀ ବିଷୟରେ ଆଲୋଚନା କଲାବେଳେ, ସମୟ ଓ ଦୂରତାକୁ ମଧ୍ୟ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ । ଉଦାହରଣ ସ୍ଵରୂପ, ଯେତେବେଳେ ଗୋଟିଏ ଯାନ ସଡ଼କ ପଥରେ ଗୋଟିଏ ସ୍ଥାନରୁ ଅନ୍ୟ ଏକ ସ୍ଥାନର ଦୂରତା ଅତିକ୍ରମ କରେ ଓ ଉକ୍ତ ଦୂରତାକୁ ଅତିକ୍ରମ କରିବାପାଇଁ ଯେଉଁ ସମୟ ନେଇଥାଏ, ତାହାକୁ ଆଧାର କରି ଏକ ସମାନ୍ତର ପ୍ରଗତି ତିଆରି କରାଯାଇପାରିବ ।

ଉଦାହରଣ – 1:
A ଓ B ମଧ୍ୟରେ ଦୂରତା 150 କି.ମି. । A ଓ B ମଧ୍ୟରେ 10 ଟି ଟ୍ରାଫିକ୍ ସଂକେତ ଅଛି । ଗୋଟିଏ କାର ଘଣ୍ଟା ପ୍ରତି 60 କି.ମି. ବେଗରେ A ରୁ ବାହାରି ସମସ୍ତ ଟ୍ରାଫିକ୍ ସଂକେତ ଅତିକ୍ରମ କରି 2 ଘଣ୍ଟା 30 ମିନିଟ୍‌ରେ B ରେ ପହଞ୍ଚେ । ମାତ୍ର ଅନ୍ୟ ଦିନ ମାନଙ୍କରେ ଅତ୍ୟଧକ ଭିଡ଼ ଯୋଗୁଁ ନିମ୍ନ ମତେ ବିଭିନ୍ନ ଟ୍ରାଫିକ୍ ସଂକେତ ପାଖରେ କାରକୁ ଠିଆ ହେବାକୁ ପଡ଼ିଥାଏ ।
ପ୍ରଥମ ଟ୍ରାଫିକ୍ ସଂକେତ : 1 ମିନିଟ୍
ଦ୍ଵିତୀୟ ଟ୍ରାଫିକ୍ ସଂକେତ : 2 ମିନିଟ୍
ଏବଂ ଦଶମ ଟ୍ରାଫିକ୍ ସଂକେତ ପର୍ଯ୍ୟନ୍ତ 10 ମିନିଟ୍
ଯଦି କାରର ଘଣ୍ଟା ପ୍ରତି ବେଗ 60 କି.ମି. ହୁଏ ଓ କାରଟି ସମସ୍ତ ଟ୍ରାଫିକ୍ ନିୟମ ପାଳନ କରେ ତେବେ ଉକ୍ତ ଯାତ୍ରାରେ କାରଟି ନେଇଥିବା ସମୟ ନିର୍ଣ୍ଣୟ କର ।
ଉ :
1 ଠାରୁ 10 ପର୍ଯ୍ୟନ୍ତ ଟ୍ରାଫିକ୍ ସଂକେତରେ ଅଟକିବା ସମୟଗୁଡ଼ିକ କ୍ରମ ଅନୁସାରେ 1, 2, 3,…., 10
∴ ଏହା ସମାନ୍ତର ଶ୍ରେଣୀ ଅଟେ । A.P. = 1, 2, 3…..10
ଏଠାରେ ପ୍ରଥମପଦ a = 1, ସାଧାରଣ ଅନ୍ତର d = 1 ଓ ପଦସଖ୍ୟା n = 10
∴ ମୋଟ ଅଟକିଥିବା ସମୟ = \(\frac{n(n + 1)}{2}\) = \(\frac{10(10 + 1)}{2}\) = 55 ମିନିଟ୍ ।
କାରର ବେଗ ଘଣ୍ଟାପ୍ରତି 60 କି.ମି. ହେଲେ ଏହା କେଉଁଠି ନ ଅଟକି 2 ଘଣ୍ଟା 30 ମିନିଟ୍‌ରେ A ଠାରୁ B ପର୍ଯ୍ୟନ୍ତ ଯାଏ ।
∴ ଟ୍ରାଫିକ୍ ସଂକେତରେ ନିର୍ଦ୍ଧାରିତ ସମୟକ୍ରମରେ ଅଟକି A ଠାରୁ B ପର୍ଯ୍ୟନ୍ତ ପହଞ୍ଚିବା ସମୟ
= 2 ଘ. 30 ମି. + 55 ମି. = 3 ଘଣ୍ଟା 25 ମିନିଟ୍ ।

ଉଦାହରଣ – 2:
ଅଶୋକ ଏକ ସଡ଼କରେ ଗାଡ଼ି ଚଳାଇ ଗଲାବେଳେ ପ୍ରଥମ, ଦ୍ୱିତୀୟ ଓ ତୃତୀୟ ଟ୍ରାଫିକ୍ ଲାଇଟ୍‌କୁ ଯଥାକ୍ରମେ 5, 12 ଓ 19 ସେକେଣ୍ଡରେ ଅତିକ୍ରମ କଲା । ଏହିପରି କ୍ରମରେ ଟ୍ରାଫିକ୍ ଲାଇଟ୍‌କୁ ଅତିକ୍ରମ କରି ଚାଲିଲେ, 75 ସେକେଣ୍ଡରେ କେଉଁ ନମ୍ବରର ଟ୍ରାଫିକ୍ ଲାଇଟ୍‌କୁ ଅତିକ୍ରମ କରିବ ?
ଉ :
ପ୍ରଥମ, ଦ୍ଵିତୀୟ ଓ ତୃତୀୟ ଟ୍ରାଫିକ୍ ଲାଇଟ୍‌ ସମୟ ଯଥାକ୍ରମେ 5, 12 ଓ 19 ସେକେଣ୍ଡ ହେବ ।
∴ ସମୟଗୁଡ଼ିକ ସମାନ୍ତର ପ୍ରଗତି ବିଶିଷ୍ଟ; AP = 5, 12, 19
∴ ଏଠାରେ ପ୍ରଥମ ପଦ a = 5, DIUINA ABQ d = 12 – 5 = 7
ମନେକର 75 ସେକେଣ୍ଡରେ ଅଶୋକ n ତମ ଟ୍ରାଫିକ୍ ଲାଇଟ୍‌କୁ ଅତିକ୍ରମ କରିବ ।
∴ t_n = 75 ସେକେଣ୍ଡରେ
∴ t_n = a + (n – 1) d
⇒ 75 = 5 + (n – 1)7 = 75 = 5 + 7n – 7
⇒ 7n – 2 – 75 = 0
⇒ 7n = 77
⇒ n = 11
∴ ଅଶୋକ 75 ସେକେଣ୍ଡରେ 11ଟି ଟ୍ରାଫିକ୍ ଲାଇଟ ଅତିକ୍ରମ କରିବ ।

ଉଦାହରଣ – 3:
କୌଣସି ସିଧା ସଡ଼କରେ ପ୍ରଥମ, ଦ୍ଵିତୀୟ ଓ ତୃତୀୟ ଟ୍ରାଫିକ ସଂକେତ ଯଥାକ୍ରମେ 3 କି.ମି., 5 କି.ମି. ଓ 7 କି.ମି. ଦୂରରେ ଲାଗିଛି ।
ଏହି କ୍ରମରେ 10ମ ଟ୍ରାଫିକ୍ ସଂକେତର ଦୂରତା କେତେ କି.ମି. ହେବ ?
ଉ :
ଦତ୍ତଅନୁସାରେ ପ୍ରଥମ, ଦ୍ୱିତୀୟ ଓ ତୃତୀୟ ଟ୍ରାଫିକ୍ ସଂକେତ ଦୂରତା ଯଥାକ୍ରମେ 3 କି.ମି., 5 କି.ମି. ଓ 7 କି.ମି. ।
ଅର୍ଥାତ୍ ଏହି ଦୂରତା ଏକ ସମାନ୍ତର ଶ୍ରେଣୀ ବିଶିଷ୍ଟ ।
∴ A. P = 3, 5, 7
ଏଠାରେ ପ୍ରଥମ ପଦ a = 3, ସାଧାରଣ ଅନ୍ତର d = 5 – 3 = 2
∴ 10 ମ ଟ୍ରାଫିକ୍ ସଂକେତର ଦୂରତା = t₁₀ ଏଠାରେ n = 10
t₁₀ = a + (n – 1) d = 3 + (10 – 1)2 = 3 + 18 = 21 କି.ମି.
∴10 ମ ସଂକେତର ଦୂରତା 21 କି.ମି. ।

ଉଦାହରଣ – 4:
କୌଣସି ସଡ଼କ ଉପରେ ଲଗାଯାଇଥିବା ଟ୍ରାଫିକ୍ ଲାଇଟଗୁଡ଼ିକର ଦୂରତା ଏକ ସମାନ୍ତର ଶ୍ରେଣୀ ବିଶିଷ୍ଟ । ଯଦି ତୃତୀୟ ଲାଇଟର ଦୂରତା 1500 ମିଟର ଏବଂ ଅଷ୍ଟମ ଲାଇଟର ଦୂରତା 3000 ମିଟର ହୁଏ, ତେବେ 15 ତମ ଲାଇଟର ଦୂରତା କେତେ ନିର୍ଣ୍ଣୟ କର ।
ଉ :
ତୃତୀୟ ଲାଇଟ୍‌ର ଦୂରତା = 1500 ମି. ଅର୍ଥାତ୍ t₃ = 1500 ମି.
ଓ ଅଷ୍ଟମ ଲାଇଟ୍‌ର ଦୂରତା = 3000 ମି. ଅର୍ଥାତ୍ t₈ = 3000 ମି.
ଏକ ସମାନ୍ତର ଶ୍ରେଣୀର n ତମ ପଦ । ହେଲେ,
t_n = a + (n – 1) d
ପ୍ରଶ୍ମାନୁସାରେ, t₃ = 1500 ଏବଂ t₈ = 3000
a + (3 – 1) d = 1500
⇒ a + 2d = 1500 …. (i)
ଏବଂ a + (8 – 1) d = 3000
⇒ a + 7d = 3000 …..(ii)
ସମୀକରଣ (ii) ରୁ (ii) କୁ ବିୟୋଗ କଲେ,
(a + 7d) − (a + 2d) = 3000 – 1500
⇒ 5d = 1500 ⇒ d = 300
‘d’ ର ମୂଲ୍ୟକୁ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ,
a + 2 × 300 = 1500 ⇒ a+ 600 = 1500 ⇒ a = 900
∴ 15-ତମ ଲାଇଟ୍‌ର ଦୂରତା
= t₁₅ = a + (15 – 1) d = 900 + 14 × 300
= 900 + 4200 = 5100 ମିଟର ।

→ ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷାରେ ପରିସଂଖ୍ୟାନର ପ୍ରୟୋଗ :

→ ଉଦ୍ଦେଶ୍ୟ – ଯାନବାହନ ଦ୍ବାରା ସୃଷ୍ଟି ପ୍ରଦୂଷଣ, ବିଭିନ୍ନ ସମୟରେ ଭିନ୍ନ ଭିନ୍ନ ସ୍ତରରେ ପହଞ୍ଚିଥାଏ । ପରିବେଶ ସୁରକ୍ଷା ଦୃଷ୍ଟିରୁ ବାୟୁମଣ୍ଡଳର ପ୍ରଦୂଷଣ ସ୍ତର କମାଇବା ଆବଶ୍ୟକ । ସେହିଭଳି ବିଭିନ୍ନ କାରଣରୁ ସଡ଼କ ଦୁର୍ଘଟଣା ଦିନକୁ ଦିନ ବଢ଼ିଚାଲିଛି । ବିଭିନ୍ନ ପ୍ରଦୂଷଣ ତଥା ସଡ଼କ ଦୁର୍ଘଟଣା ବିଷୟକ ତଥ୍ୟ ସଂଗ୍ରହ କରିବା ଓ ତାହାର ପରିସଂଖ୍ୟାନ ଭିତ୍ତିକ ଲେଖଚିତ୍ର ପ୍ରସ୍ତୁତ କରି ତାହା ମାଧ୍ୟମରେ ଜନ ସଚେତନତା ସୃଷ୍ଟି କରିବା ଏହି ପାଠ୍ୟର ଉଦ୍ଦେଶ୍ୟ ।

→ ପ୍ରସଙ୍ଗ – 1889 ଭାରତ ସରକାରଙ୍କ ମୋଟର ଯାନ ଆଇନ ଅନୁସାରେ ସବୁ ପ୍ରକାର ଡିଜେଲ ଓ ପେଟ୍ରୋଲ ଚାଳିତ ଯାନ ପାଇଁ ପ୍ରଦୂଷଣ ନିୟନ୍ତ୍ରଣ ପ୍ରମାଣ ପତ୍ର (PUC ଅର୍ଥାତ୍ Pollution Under Control) ଜରୁରୀ । ଏହା ଆଗରୁ ସେତେଟା କଡ଼ାକଡ଼ି ଭାବେ ଲାଗୁ ହେଉନଥିଲା । ଦିଲ୍ଲୀ, ବମ୍ବେ, ମାଡ୍ରାସ, ହାଇଦ୍ରାବାଦ ଓ ବାଙ୍ଗାଲୋର ଆଦି ପ୍ରମୁଖ ସହରରେ ନିକଟରେ ଏହି ଆଇନକୁ କଡ଼ାକଡ଼ି ଭାବେ ଲାଗୁ କରିବାକୁ ସରକାର ସ୍ଥିର କରିଛନ୍ତି । ଆଗରୁ କାଗଜ ତିଆରି ନିମ୍ନ ପ୍ରଦୂଷଣ ନିୟନ୍ତ୍ରଣ ପତ୍ର ଦିଆଯାଉଥିଲା । ତାହା ବେଳେ ବେଳେ ହଜି ଯାଉଥିଲା ବା ନଷ୍ଟ ହୋଇଯାଉଥିଲା । ବର୍ତ୍ତମାନ ଅକ୍ଟୋବର 1, 2019 ଠାରୁ online ପ୍ରଦୂଷଣ ନିୟନ୍ତ୍ରଣ ପ୍ରମାଣପତ୍ର ଦିଆଯାଉଛି । ଯେଉଁଥରେ କି ହଜିଯିବା ଓ ନଷ୍ଟ ହୋଇଯିବାର ଭୟ ନାହିଁ । ନୂଆ ଗାଡ଼ି ପାଇଁ ପ୍ରଦୂଷଣ ସାର୍ଟିଫିକେଟ ଏକ ବର୍ଷ ପାଇଁ ଓ ପୁରୁଣା ଗାଡ଼ି ପାଇଁ ଏହା 6 ମାସ ପାଇଁ ବୈଧ ଅଟେ । ପ୍ରଦୂଷଣ ନିୟନ୍ତ୍ରଣ ପ୍ରମାଣପତ୍ର ବିନା ଗାଡ଼ି ଚଳାଇଲେ 2000 ଟଙ୍କା କିମ୍ବା 3 ମାସ ଜେଲ (ପ୍ରଥମ ଥର ପାଇଁ), ଦ୍ଵିତୀୟ ଥର ଖିଲାପ କଲେ 4000 ଟଙ୍କା କିମ୍ବା 4 ମାସ ପର୍ଯ୍ୟନ୍ତ ଜେଲ ହେବାର ପ୍ରାବଧାନ ରହିଛି । ସଡ଼କ ଦୁର୍ଘଟଣା ଦିନକୁ ଦିନ ବଢ଼ି ବଢ଼ି
ଚାଲିବାର ପ୍ରଧାନ କାରଣଗୁଡ଼ିକ ହେଲା –
(i) ଟ୍ରାଫିକ୍ ନିୟମ ପାଳନ ନ କରି ବେପରୱା ଗାଡ଼ି ଚଳାଇବା
(ii) ନିଶାସକ୍ତ ହୋଇ ଗାଡ଼ି ଚଳାଇବା ।
(iii) ଦ୍ରୁତ ଗତିରେ ଗାଡ଼ି ଚଳାଇବା ।
(iv) ବିନା ହେଲମେଟରେ ଗାଡ଼ି ଚଳାଇବା ଇତ୍ୟାଦି ।
ଏହି ସବୁ ଦୁର୍ଘଟଣାର ହାର କମାଇବା ପାଇଁ ସରକାର ନିକଟରେ କଡ଼ା ପଦକ୍ଷେପ ନେଇଛନ୍ତି । ପୂର୍ବ ଅପେକ୍ଷା ଟ୍ରାଫିକ୍ ଜୋରିମାନା ଅତ୍ୟଧିକ ବୃଦ୍ଧି କରାଯାଇଛି ।
ନୂଆ ଟ୍ରାଫିକ୍ ଜୋରିମାନାର ଏକ ତାଲିକା ନିମ୍ନରେ ପ୍ରଦତ୍ତ ହେଲା ।

ଉଦାହରଣ – 5
ପ୍ରଦୂଷକଙ୍କ ମାତ୍ରା ଦର୍ଶାଯାଇଛି । କେଉଁ ବର୍ଷ ପ୍ରମୁଖ ପ୍ରଦୂଷକର ମାତ୍ରା ସର୍ବନିମ୍ନ ସ୍ତରରେ ପହଞ୍ଚିଲା ? ପ୍ରଦୂଷଣ ନିମ୍ନ ସ୍ତରରେ ପହଞ୍ଚାଇବା ପାଇଁ କାହାକୁ ଶ୍ରେୟ ଦିଆଯିବ ?

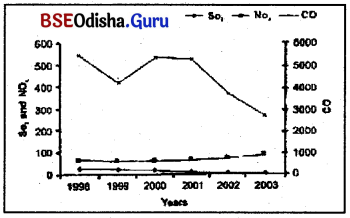
ଉ :
2003 ମସିହାରେ CO ପ୍ରଦୂଷଣ ମାତ୍ରା ସବୁଠାରୁ କମ୍ । ଏହାର ଶ୍ରେୟ ସରକାରଙ୍କର କାର୍ଯ୍ୟକ୍ରମ;
(i) ପ୍ରଦୂଷଣ ନିୟନ୍ତ୍ରଣ ପ୍ରମାଣ ପତ୍ରକୁ କଡ଼ାକଡ଼ି ଭାବେ ଲାଗୁ କରିବା ।
(ii) ଯାନମାନଙ୍କରେ ’CNG ଲଗାଇବା ପାଇଁ ସରକାର କଡ଼ା ନିୟମ କରିବା ।
(iii) ଜନଗହଳି ସ୍ଥାନମାନଙ୍କରେ ପ୍ରଦୂଷଣ ମାତ୍ରା ବିଷୟରେ ବଡ଼ ବଡ଼ ଲେଖଚିତ୍ରର ବିଜ୍ଞାପନ ମାରି ଲୋକଙ୍କୁ ସଚେତନ ସଚେତନ କରାଇବ। ।

ଉଦାହରଣ – 6.
ଦତ୍ତ ସ୍ତମ୍ଭଲେଖ ଚିତ୍ରଟି କୌଣସି ଏକ ସହରର ବିଗତ ଲୋକସଂଖ୍ୟା ବ୍ୟକ୍ତ କରୁଛି ।

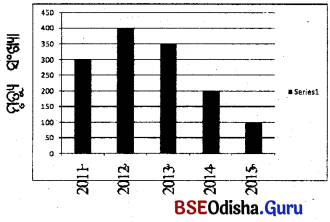
(a) 2011 – 2013 ମଧ୍ୟରେ ଦୁର୍ଘଟଣାରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ଲୋକଙ୍କ ସଂଖ୍ୟାରେ କେତେ ବୃଦ୍ଧି ବା ହ୍ରାସ୍ ହୋଇଛି ?
(b) 2012 – 2014 ମଧ୍ଯରେ ଦୁର୍ଘଟଣାରେ ମୃତ୍ୟୁ ସଂଖ୍ୟାରେ ଶତକଡ଼ା ହ୍ରାସ ବା ବୃଦ୍ଧି ନିର୍ଣ୍ଣୟ କର ।
ଉ :
ଦତ୍ତ ଲେଖଚିତ୍ର ଅନୁସାରେ
(a) 2011 ମସିହାରେ ମୃତ୍ୟୁ ସଂଖ୍ୟା = 300
2013 ମସିହାରେ ମୃତ୍ୟୁ ସଂଖ୍ୟା = 350
ବୃଦ୍ଧି = 350 – 300 = 50

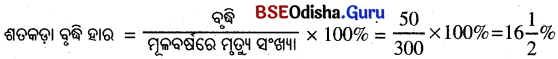
(b) 2012 ମସିହାରେ ମୃତ୍ୟୁ ସଂଖ୍ୟା = 400
2014 ମସିହାରେ ମୃତ୍ୟୁ ସଂଖ୍ୟା = 200
ହ୍ରାସ = 400 – 200 = 200

ଉଦାହରଣ – 7.
ଦିଆଯାଇଥବା ବୃତ୍ତଲେଖରେ 2018 ମସିହାରେ କୌଣସି ସହରରେ ସଡ଼କ ଦୁର୍ଘଟଣାରେ ବିଭିନ୍ନ କାରଣ ଯୋଗୁଁ ମୃତ୍ୟୁ ସଂଖ୍ୟାକୁ ଡିଗ୍ରୀରେ ବ୍ୟକ୍ତ କରାଯାଇଛି । ଯଦି ଉକ୍ତ ବର୍ଷ 10800 ଜଣ ବ୍ୟକ୍ତି ସଡ଼କ ଦୁର୍ଘଟଣାରେ ମୃତ୍ୟୁବରଣ କରିଥା’ନ୍ତି, ତେବେ ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନର ଉତ୍ତର ଦିଅ ।

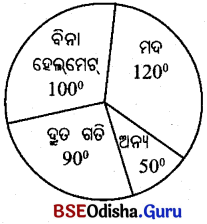
(a) ମଦ ପିଇ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ସଂଖ୍ୟା କେତେ ?
(b) ଦ୍ରୁତଗତିରେ ଗାଡ଼ି ଚଳାଇ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ସଂଖ୍ୟା କେତେ ?
ଉ :
ସମୁଦାୟ ଦୁର୍ଘଟଣାରେ ମୃତ୍ୟୁ ସଂଖ୍ୟା = 10800
∴ ବୃତ୍ତାକାର ହେତୁ ଏହାର ଡିଗ୍ରୀ ପରିମାପ = 360°
(a) ମଦ ପିଇ ଗାଡ଼ି ଚଳାଇ ଦୁର୍ଘଟଣାରେ ପଡ଼ିଥିବା ବ୍ୟକ୍ତିଙ୍କ ଡିଗ୍ରୀ ପରିମାପ = 120°
ଏହାର ସଂଖ୍ୟା = \(\frac{10800}{360°}\) × 120° = 3600 ଜଣ ।

(b) ଦ୍ରୁତଗତିରେ ଗାଡ଼ି ଚଳାଇ ମୃତ୍ୟୁବରଣ କରିଥିବା ସଂଖ୍ୟାର ଡିଗ୍ରୀ ପରିମାପ = 90°
ଏହାର ସଂଖ୍ୟା = \(\frac{10800}{360°}\) × 90° = 2700 ଜଣ ।

→ ଉଦ୍ଦେଶ୍ୟ – ଦିନକୁ ଦିନ ବଢୁଥ‌ିବା ସଡ଼କ ଦୁର୍ଘଟଣାକୁ ଏଡ଼ାଇବା ପାଇଁ ରାତିରେ ସଡ଼କମାନଙ୍କରେ ଉଜ୍ଜ୍ବଳ ଆଲୋକର ବ୍ୟବସ୍ଥା କରାଯାଇଥାଏ । ଟ୍ରାଫିକ୍ ନିୟମ ଉଲ୍ଲଙ୍ଘନକାରୀଙ୍କୁ ଚିହ୍ନଟ କରିବାପାଇଁ ମଧ୍ୟ ସଡ଼କର ବିଭିନ୍ନ ସ୍ଥାନରେ CCTV କ୍ୟାମେରା ଲଗାଯାଇଥାଏ । ଏହି ସବୁ ବ୍ୟବସ୍ଥାରେ ତ୍ରିକୋଣମିତିକୁ କିପରି ପ୍ରୟୋଗ କରାଯାଇପାରିବ ତାହା ଏହି ପାଠ୍ୟର ଲକ୍ଷ୍ୟ ।

→ ପ୍ରସଙ୍ଗ – ସାଧାରଣତଃ ବଡ଼ ବଡ଼ ଖୁଣ୍ଟ ଉପରେ ବା ରାସ୍ତା କଡ଼ରେ ଥ‌ିବା ବଡ଼ ବଡ଼ ଅଟ୍ଟାଳିକା, ଟାୱାର ଉପରେ ଆଲୋକ ଓ CCTV ବ୍ୟବସ୍ଥା କରାଯାଇଥାଏ । ତ୍ରିକୋଣମିତିରେ ଥ‌ିବା ଉଚ୍ଚତା ଓ ଦୂରତା (Height and distance)

ଉଦାହରଣ – 8
12 ସେ.ମି. ଉଚ୍ଚ ଏକ ସ୍ତମ୍ଭ ଉପରେ ଗୋଟିଏ CCTV କ୍ୟାମେରା ଏପରି ଭାବେ ଖଞ୍ଜି ଦିଆଯାଇଛି ଯେ ସ୍ତମ୍ଭ ଉପରୁ ଲକ୍ଷ୍ୟ କଲେ 13 ସେ.ମି. ଦୀର୍ଘ ଦୃଷ୍ଟି ରେଖା (Line of sight) ଆଗକୁ ଚଳାଚଳ କରୁଥିବା ଯାନବାହନ (Traffic) ସବୁ ଦୃଷ୍ଟିଗୋଚର ହୁଏ ।

ଯଦି ସତ୍ୟ,
(i) ସ୍ତମ୍ଭର ପାଦଦେଶରୁ ଯେଉଁ ସ୍ଥାନ ପରେ ଟ୍ରାଫିକ୍ ଦୃଷ୍ଟିଗୋଚର ହୁଏ, ତା’ର ଦୂରତା ନିର୍ଣ୍ଣୟ କର ।
(ii) ସ୍ତମ୍ଭର ଚତୁଃପାର୍ଶ୍ଵରେ ଥ‌ିବା କେତେ ପରିମିତ ସ୍ଥାନକୁ ଘାସରେ ଆଚ୍ଛାଦିତ କରାଯାଇପାରିବ ? (green belt)
(iii) ତୁମେ ଭାବୁଛ କି CCTV କ୍ୟାମେରାଗୁଡ଼ିକ ପ୍ରକୃତରେ ଟ୍ରାଫିକ ନିୟନ୍ତ୍ରଣରେ ସାହାଯ୍ୟକାରୀ ?
ଉ :

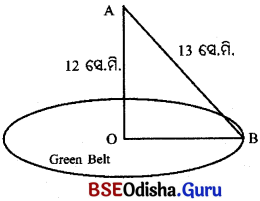
(i) ଦୀର୍ଘ ଦୃଷ୍ଟି ରେଖା AB = 13 ସେ.ମି. ।
ସ୍ତମ୍ଭର ଉଚ୍ଚତା OA = 12 ସେ.ମି.,
ତାହା ସ୍ତମ୍ଭର ପାଦଦେଶରୁ ଯେଉଁ ସ୍ଥାନ ପରେ ଟ୍ରାଫିକ
AOB ସମକୋଣୀ ∆ରେ
= OB = \(\sqrt{AB^2 – OA^2}\)
= \(\sqrt{(13)^2-(12)^2}\)
= \(\sqrt{169-144}\) = √25 =5 ସେ.ମି. ।

(ii) ସ୍ତମ୍ଭ ଚାରିପଟେ ଥିବା OB ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ବୃତ୍ତାକାର କ୍ଷେତ୍ରରେ ଟ୍ରାଫିକ ଦୃଶ୍ୟମାନ ହେବ ନାହିଁ । ଉକ୍ତ ବୃତ୍ତାକାର କ୍ଷେତ୍ରରେ ଘାସ ଆଚ୍ଛାଦିତ (Green belt) କରାଯାଇପାରେ ।
∴ ଉକ୍ତ ପଡ଼ିଆର କ୍ଷେତ୍ରଫଳ = tr = π OB² (r = OB)
= π.5² ସେ.ମି. = 25π ସେ.ମି.

(iii) ଟ୍ରାଫିକ୍ ନିୟନ୍ତ୍ରଣ ପାଇଁ CCTV କ୍ୟାମେରାର ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଭୂମିକା ରହିଛି ।
ଟ୍ରାଫିକ୍ ନିୟମ ଖୁଲାପକାରୀ CCTV କ୍ୟାମେରା ଦ୍ଵାରା ଧରାପଡ଼ି ଥା’ନ୍ତି ।

ଉଦାହରଣ – 9
ଏକ ଚାରିଛକ ପାଖରେ ଏକ ଖମ୍ବର ଶୀର୍ଷ ଦେଶରେ ଏକ CCTV କ୍ୟାମେରା ଲାଗିଛି । ଉକ୍ତ କ୍ୟାମେରାରୁ ସଡ଼କ ଉପରେ ଥ‌ିବା ଏକ କାରର କୌଣିକ ଅବନତି 45 । ଖମ୍ବର ପାଦଦେଶରୁ କାରର ଦୂରତ୍ବ 10 ମିଟର ହେଲେ ଖମ୍ବର ଉଚ୍ଚତା
କେତେ ?
ଉ :

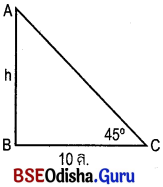
AB ଖମ୍ବର ଶୀର୍ଷ ଦେଶରେ ଅର୍ଥାତ୍ A ଠାରେ CCTV କ୍ୟାମେରା ଲାଗିଛି ।
ଏହାର ପାଦଦେଶ ‘B’ ଠାରୁ 10 ମି. ଦୂର ‘C’ ଠାରେ ଏକ କାରର କୌଣିକ ଅବନତି = 45°
ABC ସମକୋଣୀ ତ୍ରିଭୁଜରେ BC = 10 ମି. ଓ ∠BCA = 45°
tan 45°= \(\frac{AB}{BC}\)
⇒ 1 = \(\frac{AB}{10}\) ⇒ AB = 10 ମିଟର ।
∴ ଖମ୍ବର ଉଚ୍ଚତା 10 ମିଟର ।

ଉଦାହରଣ – 10
ଏକ 8 ମିଟର ଉଚ୍ଚ ଖମ୍ବ ଉପରେ ସଡ଼କରେ ଯାତାୟତ ନିୟନ୍ତ୍ରଣ ପାଇଁ ଏକ କ୍ୟାମେରା ଲାଗିଛି । କ୍ୟାମେରାଟି ଖମ୍ବର ଶୀର୍ଷରୁ 17 ମିଟର ଦୂର ଦୃଷ୍ଟିରେଖା ପର୍ଯ୍ୟନ୍ତ ଯାତାୟତ ଦେଖିପାରେ । କ୍ୟାମେରାଟି ଖମ୍ବର ଚାରିପଟେ କେତେ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ କ୍ଷେତ୍ରର ଯାତାୟତ ନିୟନ୍ତ୍ରଣ କରିପାରିବ ?
ଉ :
ଚିତ୍ରାନୁସାରେ, ଖମ୍ବର ଉଚ୍ଚତା AB = 8
ମିଟର ଦୃଷ୍ଟିରେଖା AC = 17 ମିଟର
ସମକୋଣୀ A ABC ରେ AC² = BC² + AB²
⇒ 17² = BC² + 8²
⇒ BC² = 17² – 8² = 15²
⇒ BC = 15
କ୍ୟାମେରା ଦ୍ବାରା ଖମ୍ବର ଚାରିପଟେ ଦର୍ଶନୀୟ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = π(BC)²
= 3.14 × 225 = 706.5 ମିଟର

→ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷାର ଦୁଇ ଚଳ ରାଶି ବିଶିଷ୍ଟ ସମସ୍ୟା :
ଉଦ୍ଦେଶ୍ୟ – ସଡ଼କରେ ଦୃଶ୍ୟ ଉପରେ ଆଧାରିତ ସମସ୍ୟାମାନଙ୍କ ସାହାଯ୍ୟରେ ନିମ୍ନ ସମୀକରଣକୁ ସମାଧାନ କରିବା ହେଲା ଏହି ଦ ର ଉଦ୍ଦେଶ୍ୟ ।

→ ସମୀକରଣ – ପ୍ରତିକ୍ରିୟା ଦୂରତା + ବେଗ କ୍ଷୟ ଦୂରତା = ସ୍ଥିରତା ଆସିବା ଦୂରତା
ସ୍ଥିରତା ଆସିବା ଦୂରତା = ପ୍ରତିକ୍ରିୟା ଦୂରତା × ପିଛା କରିବା ଦୂରତା

→ ପିଛା କରିବା ଦୂରତା (Chasing distance) :
ଆଗରେ ଯାଉଥ‌ିବା ଯାନକୁ ପିଛା କରିବା ଦୂରତା ସାଧାରଣତଃ ସେକେଣ୍ଡରେ ନିର୍ଦ୍ଧାରିତ କରାଯାଏ । ଏହାକୁ ପ୍ରତିକ୍ରିୟା ଦୂରତା ଓ ସ୍ଥିରତା ଆସିବା ଦୂରତା ଦ୍ଵାରା ହିସାବ କରାଯାଏ ।

ଉଦାହରଣ – 11
ତଳର ସାରଣୀରେ ହିସାବ କରି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

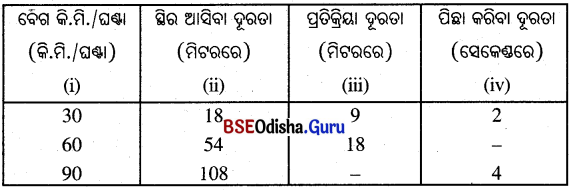
ଉ :
(i) ସମ୍ପୂର୍ଣ୍ଣ ସ୍ଥିରତା ଆସିବା ଦୂରତ୍ବ = ପ୍ରତିକ୍ରିୟା ଦୂରତ୍ୱ x ପିଛା କରିବା ଦୂରତ୍ୱ
ପ୍ରଥମ ଶୂନ୍ୟସ୍ଥାନ ପାଇଁ ସ୍ଥିରତା ଆସିବା ଦୂରତା = 54 ମି.
ଓ ପ୍ରତିକ୍ରିୟା ଦୂରତା = 18 ମି.
∴ ପିଛା କରିବା ଦୂରତା = \(\frac{54}{18}\) ମି. = 3 ମି.

(ii) ଦ୍ଵିତୀୟ ଶୂନ୍ୟସ୍ଥାନ ପାଇଁ ସ୍ଥିରତା ଆସିବା ଦୂରତା = 108 ମି.
ଓ ପିଛା କରିବା ଦୂରତା = 4 ମି.
∴ ପ୍ରତିକ୍ରିୟା ଦୂରତା = \(\frac{108}{4}\) = 27 ମି.

ପୂରଣ ସାରଣୀଟି ହେବ –

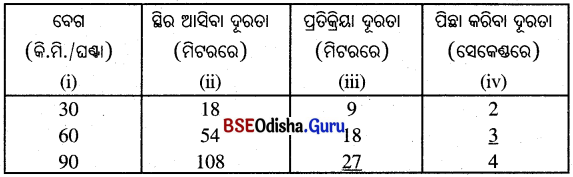
ବେଗ ସମ୍ବନ୍ଧୀୟ ସମୀକରଣ :
(i) v = u + at
(ii) v² = u² + 2as
ଏଠାରେ v = ଅନ୍ତିମ ବେଗ, u = ପ୍ରାରମ୍ଭିକ ବେଗ, a = ତ୍ୱରଣ, t = ସମୟ

ଉଦାହରଣ – 12
ଗୋଟିଏ କାର୍‌ର ଘଣ୍ଟା ପ୍ରତି ବେଗ 50 କି.ମି. । ଯଦି ସ୍ଥିରତାକୁ ଆସିବାର ଦୂରତା 40 ମିଟର ଓ ମନ୍ଦିତ ବେଗ 4.4 ମି./ସେକେଣ୍ଡ ହୁଏ ତେବେ କାରଟି କେତେ ସମୟ ପରେ ସ୍ଥିର ହେବ ?
ଉ :
କାରର ପ୍ରାରମ୍ଭିକ ବେଗ u = 50 କି.ମି. | ଘଣ୍ଟା = 50 × \(\frac{5}{18}\) = \(\frac{129}{9}\) ମିଟର / ସେକେଣ୍ଡ
ସ୍ଥିରତାକୁ ଆସିବାର ଦୂରତା s = 40 ମିଟର
ମିଟର ବେଗ = 4.4 ମିଟର / ସେକେଣ୍ଡ
⇒ a = – 4.4 ମିଟର / ସେକେଣ୍ଡ
ବେଗର ପ୍ରଥମ ସମୀକରଣ ଅନୁସାରେ : v = u + at (v = ଶେଷ ବେଗ, ସ୍ଥିରତା ସମୟରେ v = 0)
⇒ 0 = \(\frac{129}{9}\) – 4.4 t
⇒ 4.4t = \(\frac{129}{9}\)
⇒ t = \(\frac{125}{9×4.4}\) = t = \(\frac{1250}{396}\)
⇒ t = 3.16
∴ କାର୍ ସ୍ଥିର ହେବା ପାଇଁ 3.16 ସେକେଣ୍ଡ ଲାଗିବ ।

ସୂତ୍ରାବଳୀ (Formulae)

→ ସମାନ୍ତର ପ୍ରଗତି :
ପ୍ରଥମ ପଦ = a
ସାମାରଣ ଅନ୍ତର = d
∴ n-ତମ ପଦ = t_n = a + (n – 1) d
n ସଂଖ୍ୟକ ପଦର ଯୋଗାଗଫଳ S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
ପ୍ରଥମ n ସଂଖ୍ୟକ ଗଣନ ସଂଖ୍ୟାର ସମଷ୍ଟି = 1 + 2 + 3 + ………. + n = \(\frac{n(n+1)}{2}\)
ବୃତ୍ତଲେଖ :
ସମସ୍ତ ବୃତ୍ତକଳାର କେନ୍ଦ୍ରୀୟ କୋଣର ପରିମାଣର ସମଷ୍ଟି = 360°

→ ତ୍ରିକୋଣମିତି :
ଉଚ୍ଚତା ଓ ଦୂରତା

→ ଦୁଇଚଳ ରାଶି ବିଶିଷ୍ଟ ସମସ୍ୟା –
ପ୍ରତିକ୍ରିୟା ଦୂରତା + ବେଗ କ୍ଷୟ ଦୂରତା = ସ୍ଥିରତା ଆସିବା ଦୂରତା ।
ପ୍ରତିକ୍ରିୟା ଦୂରତା = ସ୍ଥିରତା ଆସିବା ଦୂରତା – ବେଗ କ୍ଷୟ ଦୂରତା
ବେଗ କ୍ଷୟ ଦୂରତା = ସ୍ଥିରତା ଆସିବା ଦୂରତା – ପ୍ରତିକ୍ରିୟା ଦୂରତା
ସ୍ଥିରତା ଆସିବା ଦୂରତା = ପ୍ରତିକ୍ରିୟା ଦୂରତା × ପିଛାକରିବା ଦୂରତା ।