Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(b)
Questioin 1.
ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର, ଯେଉଁ ବୃତ୍ତର
(i) ବ୍ୟାସାର୍ଦ୍ଧ 31.5 ମିଟର
(ii) ବ୍ୟାସ 112 ସେ.ମି.
(iii) ପରିଧି 286 ସେ.ମି.
(iv) ଅର୍ଥପରିଧୂ 44 ମି.
ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 ବର୍ଗ ଏକକ ।
(i) gæ qua (r) = 31.5 ମି.
∴ ଦରର ବ୍ୟାସାଦ = πr2 = \(\frac { 22 }{ 7 }\) × 31.5 × 31.5 ଦା. ସେ.ମି.
= 22 × 4.5 × 31.5 ଦା ମି. = 3118.5 ଦା ମି.
(ii) ବୃତ୍ତର ବ୍ୟାସ = 112 ସେ.ମି. ⇒ ବ୍ୟାସାର୍ଦ୍ଧ (r) = \(\frac { 22 }{ 7 }\) = 56 ସେ.ମି.
∴ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 = \(\frac { 22 }{ 7 }\) × 56 × 56 ବର୍ଗ ସେ.ମି. = 9856 ସେ.ମି.
(iii) ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି. । ବୃତ୍ତର ପରିସ୍ = 2πr ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 2πr = 286
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 286 ⇒ r = \(\frac{286 \times 7}{2 \times 22}\) = 45.5 ସେ.ମି.
∴ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 = \(\frac { 22 }{ 7 }\) × 45.5 × 45.5 ବର୍ଗ ସେ.ମି. = 6506.5 ବର୍ଗ ସେ.ମି.
(iv) ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି. । ବୃତ୍ତର ଅର୍ଦ୍ଧପରିଧ୍ = πr ମି.
ପ୍ରଶ୍ନନୁସାରେ, πr = 44
⇒ \(\frac { 22 }{ 7 }\) × r = 44 ⇒ r = \(\frac{44 \times 7}{22}\) = 14 ମି.
∴ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 = \(\frac { 22 }{ 7 }\) × 14 × 14 = 616 ବୃ ସେ.ମି.
![]()
Question 2.
(i) ବୃତ୍ତର କ୍ଷେତ୍ରପଳ 154 ବର୍ଗମିଟର ହେଲେ, ଏହାର ବ୍ୟାସର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(ii) ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ 7546 ବର୍ଗମିଟର ହେଲେ, ଏହାର ପରିଧ୍ କେତେ ?
Solution:
(i) ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ = r ମି. । ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 ବୃ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, πr2 = 154
⇒ \(\frac { 22 }{ 7 }\) × r2 = 154 ⇒ r2 = \(\frac{154 \times 7}{22}\) = 49 ⇒ r = 7 ମି.
∴ ବୃତ୍ତର ବ୍ୟାପ = 2r = 2 × 7 = 14 ମି. |
(ii) ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି. । ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 ବର୍ଗ ମି.
ପ୍ରଶ୍ନନୁସାରେ, πr2 = 7546
⇒ \(\frac { 22 }{ 7 }\) × r2 = 7546 ⇒ r2 = \(\frac{7546 \times 7}{22}\) = 343 × 7 ⇒ r = \(\sqrt{343 \times 7}\) = 49 ମି.
∴ ବୃତ୍ତର ବ୍ୟାପ = 2πr = 2 × \(\frac { 22 }{ 7 }\) × 49 = 308 ମିଟର |
Question 3.
ଦ୍ରଭକଲାଭ ସେତ୍ରପଳ ନିଶ୍ରୟ କର ଯେଉ ଦ୍ରରକଳାତ
(i) ଚାପର ଡିଗ୍ରୀ ପରିମାପ 120°, ବ୍ୟାସାର୍ଦ୍ଧ 28 ସେ.ମି. ।
(ii) ସଂପୃକ୍ତ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ 7546 ବର୍ଗ ମି. ଓ ସଂପୃକ୍ତ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 105° |
(iii) ସଂପୃକ୍ତ ବୃତ୍ତର ପରିସ୍ 396 ମିଟର ଏବଂ ଚାପର ଦୈର୍ଘ୍ୟ 36 ମିଟର |
(iv) ଚାପର ଦୈର୍ଘ୍ୟ 66 ମିଟର ଏବଂ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 70° |
Solution:
ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac{\theta}{360^{\circ}}\) ଅଥବା \(\frac { 1 }{ 2 }\)Lr ବର୍ଗ ଏକକ ।
L = ଚାପର ଦୈର୍ଘ୍ୟ, r = ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ ।
(i) ଦ୍ରରକାଳାର ଚାପର ଭିଗ୍ରା ପରିମାପ (θ) = 120°, ବ୍ୟାସାର୍ଦ୍ଧ (r) = 28 ସେ.ମି.|
∴ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { θ }{ 360 }\) × πr2
= \(\frac{120}{360^{\circ}}\) × \(\frac { 22 }{ 7 }\) × 28 × 28 = \(\frac{88 \times 28}{3}\) = \(\frac { 2464 }{ 3 }\) = 821\(\frac { 1 }{ 3 }\) ବର୍ଗ ସେ.ମି.|
(ii) ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = 7546 ବର୍ଗ ମି., ବୃତ୍ତ କଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ (θ) = 105°
∴ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac{120}{360^{\circ}}\) × କଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { 105 }{ 360 }\) × 7546
= \(\frac { 26411 }{ 12 }\) ବର୍ଗ = 2200 ବ.ମି. \(\frac { 11 }{ 12 }\) ବ.ମି.
(iii) ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି. । ବୃତ୍ତର ପରିଧ୍ = 2πr ମି.
ପ୍ରଶ୍ନନୁସାରେ, 2лr = 396
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 396 ⇒ r = 396 × \(\frac { 7 }{ 44 }\) = 63 ମି.
ଚାପର ଦୈର୍ଘ୍ୟ (L) = 36 ମି.
∴ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × Lr = \(\frac { 1 }{ 2 }\) × 36 × 63 = 1134 ବ.ମି.
(iv) ମନେକର ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଷ = r ମି. |
ଚାପର ଦୈର୍ଘ୍ୟ (L) = 66 ମି., ଚାପର ଡିଗ୍ରୀ ପରିମାପ (θ) = 70°
ଆମେ ଜାଣିଛେ, L = \(\frac{θ}{180^{\circ}}\) × πr
⇒ 66 = \(\frac { 70 }{ 180 }\) × \(\frac { 22 }{ 7 }\) × r = \(\frac{66 \times 180 \times 7}{70 \times 22}\) = 54 ମି.
∴ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × Lr = \(\frac { 1 }{ 2 }\) = × 66 × 54 ବ.ମି. = 1782 ବ.ମି.
Question 4.
ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର, ଯାହାର
(i) କ୍ଷେତ୍ରଫଳ 1848 ବର୍ଗମିଟର ଓ ସଂପୃକ୍ତ ଚାପର ଡିଗ୍ରୀ
(ii) କ୍ଷେତ୍ରଫଳ 48.4 ବର୍ଗ ଡେକାମିଟର ଓ ଚାପର ଦୈର୍ଘ୍ୟ
Solution:
(i) ମନେକର ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଷର ଦୈର୍ଘ୍ୟ = r ମି., ଚାପର ଡିଗ୍ରୀ ପରିମାପ (θ) = 120°
ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac{\theta}{360^{\circ}}\) × πr2 ⇒ 1848 = \(\frac { 120 }{ 360 }\) × \(\frac { 22 }{ 7 }\) × r2
⇒ r2 = \(\frac{1848 \times 360 \times 7}{120 \times 22}\) = 1764 ⇒ r = \(\sqrt{1764}\) = 42 ମି.
∴ ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ 42 ମିଟର ।
(ii) ମନେକର ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ = r ମି., ଚାପର ଦୈର୍ଘ୍ୟ (L) = 121 ମି.
ଡେକାମିଟର କ୍ଷେତ୍ରଫଳ = 48.4 ଚା ଦୈର୍ଘ୍ୟ = 48.4 × 100 ଦୈର୍ଘ୍ୟ = 4840 ସେ.ମି.|
ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × Lr = \(\frac { 1 }{ 2 }\) × 121 r ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, \(\frac { 1 }{ 2 }\) × 121 r = 4840 ⇒ r = \(\frac{4840 \times 2}{121}\) = 80 ମି.
∴ ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ 80 ମିଟର ।
![]()
Question 5.
ବୃତ୍ତକଳାର ସଂପୃକ୍ତ ଚାପର ଡିଗ୍ରୀ ପରିମାପ ନିର୍ଣ୍ଣୟ କର :
(i) ଯାହାର ବ୍ୟାସାର୍ଦ୍ଧ 36 ମିଟର, କ୍ଷେତ୍ରଫଳ 792. ବର୍ଗମିଟର ।
(ii) ଯାହାର କ୍ଷେତ୍ରଫଳ 924 ବର୍ଗ ସେ.ମି. ଓ ସଂପୃକ୍ତ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ 2464 ବର୍ଗ ସେ.ମି. ।
(iii) ଯାହାର କ୍ଷେତ୍ରଫଳ 231 ବର୍ଗ ମିଟର ଓ ଚାପର ଦୈର୍ଘ୍ୟ 22 ମିଟର ।
Solution:
ସମାଧାନ :
(i) ମନେକର ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ = θ°, ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 36 ମି.
ଡେକାମିଟର କ୍ଷେତ୍ରଫଳ = \(\frac{\theta}{360^{\circ}}\) × πr2
⇒ 792 = \(\frac { θ }{ 360 }\) × \(\frac { 22 }{ 7 }\) × 36 × 36 ⇒ θ = \(\frac{792 \times 360 \times 7}{22 \times 36 \times 36}\) = 70°
∴ ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ 70° |
(ii) ମନେକର ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ = θ° |
ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = 2464 ବର୍ଗ ସେ.ମି., ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = 924 ବର୍ଗ ସେ.ମି.
ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac{\theta}{360^{\circ}}\) × ଚାପର କ୍ଷେତ୍ରଫଳ
⇒ 924 = \(\frac { θ }{ 360 }\) × 2464 ⇒ θ = \(\frac{924 \times 360}{2464}\) = 135°
∴ ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ 135° |
(iii) ମନେକର ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି., ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ (L) = 22 ମି. ।
∴ ବୃରକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × Lr
⇒ 231 = \(\frac { 1 }{ 2 }\) × 22 × r ⇒ r = \(\frac{231 \times 2}{22}\) = 21 ମି. ।
ମନେକର ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ = θ°
ଚାପର ଦୈର୍ଘ୍ୟ (L) = \(\frac{\theta}{180^{\circ}}\) × πr, ⇒ 22 = \(\frac { θ }{ 180 }\) × \(\frac { 22 }{ 7 }\) × 21
⇒ θ = \(\frac{22 \times 180 \times 7}{22 \times 21}\) = 60
∴ ମନେକର ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ = 60° |
Question 6.
ଦୁଇଟି ଏକକେନ୍ଦ୍ରିକ ବୃତ୍ତର ଚାପର ଡିଗ୍ରୀ ପରିମାପ ସମାନ ହେଲେ ସଂପୃକ୍ତ ବୃତ୍ତକଳା ଦ୍ୱୟର କ୍ଷେତ୍ରଫଳର ଅନ୍ତର
(i) ଚାପ ଦୁଇଟିର ଦୈର୍ଘ୍ୟର ଅନ୍ତର 25 ମି. ଓ ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ବୟର ସମଷ୍ଟି 80 ମି. ।
(ii) ଚାପ ଦୁଇଟିର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 50 ସେ.ମି. ଓ ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ବୟର ଅନ୍ତର 24 ସେ.ମି. ।
Solution:
(i) ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ ଦ୍ବୟର ଅନ୍ତର
= \(\frac { 1 }{ 2 }\) × ଚାପ ଦୁଇଟିର ଦୈର୍ଘ୍ୟର ଅନ୍ତର × ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମଷ୍ଟି
\(\frac { 1 }{ 2 }\) × 25 × 80 = 1000 ସେ.ମି.
(ii) ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ ଦ୍ଵୟର ଅନ୍ତର = \(\frac { 1 }{ 2 }\) × ବ୍ୟାସାର୍କ ଦ୍ବୟର ଅନ୍ତର × ଚାପ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି = \(\frac { 1 }{ 2 }\) × 24 × 50 = 600 ସେ.ମି. ।
Question 7.
ଗୋଟିଏ ବୃତ୍ତର କ୍ଷେତ୍ରପଳ x ବର୍ଗ ଏକକ । ଏହାର
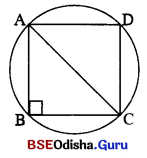
(i) ଅନ୍ତର୍ଲିଖ ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ପୂର ଦୈର୍ଘ୍ୟ କେତେ ?
(ii) ଅନ୍ତର୍ଲିଖ ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
(iii) ଅନ୍ତର୍ଲିଖ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
Solution:
ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = × ଏକକ ⇒ πr2 = x ⇒ r2 = \(\frac { x }{ π }\) ⇒ r = \(\sqrt{\frac{x}{\pi}}\) ଏକକ
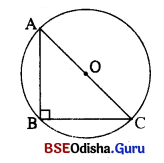
(i) ବୃତ୍ତ ମଧ୍ଯରେ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅନ୍ତର୍ଲିଖ ହେଲେ, ବୃତ୍ତର କେନ୍ଦ୍ର କଣ୍ଠର ମଧ୍ୟବିନ୍ଦୁ ହେବ ।
ଅର୍ଥାତ୍, ବୃତ୍ତର ବ୍ୟାସ = ସମକୋଣୀ ତ୍ରିଭୁଜର କଣ୍ଠର ଦୈର୍ଘ୍ୟ
⇒ AC = 2r = 2\(\sqrt{\frac{x}{\pi}}\) ଏକକ
∴ ଅନ୍ତର୍ଲିଖ ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ପୂର ଦୈର୍ଘ୍ୟ 2\(\sqrt{\frac{x}{\pi}}\) ଏକକ |
(ii) ବୃତ୍ତ ମଧ୍ୟରେ ଏକ ବର୍ଗଚିତ୍ର ଅନ୍ତର୍ଲିଖତ ହେଲେ, ବର୍ଗଚିତ୍ରର କର୍ପୂର ଦୈର୍ଘ୍ୟ = ବୃତ୍ତର ବ୍ୟାସ
⇒ AC = 2\(\sqrt{\frac{x}{\pi}}\)
ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = କେନ୍ଦ ବ୍ୟାସାର୍ଦ୍ଧ / √2 = \(\frac{2 \sqrt{\frac{x}{\pi}}}{\sqrt{2}}\) = \(\sqrt{\frac{2 x}{\pi}}\) ଏକକ
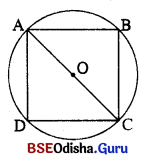
∴ ତ୍ରିଭୁଜର କର୍ପୂର ଦୈର୍ଘ୍ୟ \(\sqrt{\frac{2 x}{\pi}}\) ଏକକ
(iii) ABC ବୃତ୍ତରେ ଏକ ସମବାହୁ ଅନ୍ତର୍ଲିଖ ।
ପରିବୃତ୍ତର କେନ୍ଦ O | ବ୍ୟାସାର୍ଦ୍ଧ (OB) = \(\sqrt{\frac{x}{\pi}}\) |
△OBD ରେ m∠OBD = 30°
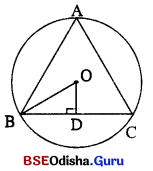
cos 30° = \(\frac { BD }{ OB }\) ⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac { BD }{ OB }\)
⇒ 2BD = √3OB ⇒ BC= √3OB ⇒ BC = √3 × \(\sqrt{\frac{x}{\pi}}\)
∴ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ ଦ୍ଵୟର ଅନ୍ତର = \(\sqrt{\frac{3x}{\pi}}\) ଏକକ |
![]()
Question 8.
ଦୁଇଟି ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ 42 ସେ.ମି. ଓ 56 ସେ.ମି. । ଅନ୍ୟ ଏକ ତୃତୀୟ ବୃତ୍ତର କ୍ଷେତ୍ରପଳ ପ୍ରଥମୋକ୍ତ ବୃତ୍ତଦ୍ୱୟର କ୍ଷେତ୍ରପଳର ସମଷ୍ଟି ସହିତ ସମାନ ହେଲେ ତୃତୀୟ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପ୍ରଥମ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = 42 ସେ.ମି. ହେଲେ କ୍ଷେତ୍ରଫଳ = x × (42)2 ବର୍ଗ ସେ.ମି.
ଦ୍ୱିତୀୟ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = 56 ସେ.ମି. ହେଲେ କ୍ଷେତ୍ରଫଳ = π × (56)2 ବର୍ଗ ସେ.ମି.
ମନେକର ତୃତୀୟ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = R ସେ.ମି. ତେବେ କ୍ଷେତ୍ରଫଳ = πR2 ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନଗୁଡ଼ିକର , πR2 = π × (42)2 + π × (56)2 ⇒ πR2 = π (422 + 562)
R = \(\sqrt{42^2+56^2}\) = \(\sqrt{1764+3136}\) = \(\sqrt{4900}\) = 70 ସେ.ମି. |
Question 9.
ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଗୋଟିଏ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ ସହିତ ସମାନ । ସେମାନଙ୍କର ପରିସୀମାର ଅନୁପାତ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ a ଏକକ ।
⇒ କ୍ଷେତ୍ରଫଳ = a2 ବର୍ଗ ଏକକ
ପୁନଶ୍ଚ, ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ ହେଲେ କ୍ଷେତ୍ରଫଳ = πr2 ବର୍ଗ ଏକକ
ପ୍ରଶ୍ନଗୁଡ଼ିକର , a2 = πr2 ⇒ \(\frac{a^2}{r^2}\) = \(\frac { π }{ 1 }\) ⇒ \(\frac { a }{ r }\) = √π
∴ବର୍ଗକ୍ଷେତ୍ରର ପରିପାପା / ଦରର ପରିସ୍ = \(\frac{4 a}{2 \pi r}\) = \(\frac{2 a}{\pi r}\) = \(\frac { 2 }{ π }\) × √π = \(\frac{2}{\sqrt{\pi}}\)
∴ବର୍ଗକ୍ଷେତ୍ର ଓ ବୃତ୍ତର ପରିସୀମାର ଅନୁପାତ 2 : √π |
Question 10.
ଗୋଟିଏ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 5 ସେ.ମି. । ଏହାର 9 ଗୁଣ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ?
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = 5 ସେ.ମି. ⇒ କ୍ଷେତ୍ରଫଳ = π × (5)2 ବର୍ଗ ସେ.ମି.
ମନେକର ଅନ୍ୟ ଏକ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି., ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନଗୁଡ଼ିକର , лг2 = 9 × л × (5)2 ⇒ r2 = 9 × (5)2 ⇒ r = 3 × 5 = 15 ସେ.ମି.
∴ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 15 ସେ.ମି. ।
Question 11.
ଗୋଟିଏ ବୃତ୍ତର ପରିଧ୍ ଯେତେ ଏକକ ଏହାଦ୍ଵାରା ଆବଦ୍ଧ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ସେତିକି ବର୍ଗ ଏକକ ହେଲେ ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ?
ସମାଧାନ : ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ଏକକ
ବୃତ୍ତର ପରିସ୍ = 2πr ଏକକ ଓ କ୍ଷେତ୍ରଫଳ = πr2 ବର୍ଗ ଏକକ
ପ୍ରଶ୍ନନୁସାରେ, 2πr = πr2, = r = 2 ଏକକ
∴ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 2 ଏକକ ।
Question 12.
ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ C ବର୍ଗ ଏକକ । ଏହାର ଅନ୍ତର୍ଲିଖ୍ ଓ ପରିଲିଖ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ?
Solution:
ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = C ବର୍ଗ ଏକକ
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = √C ଏକକ
(i) ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ର ମଧ୍ୟରେ ବୃତ୍ତଟିଏ ଅନ୍ତର୍ଲିଖ
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = ଅନ୍ତର୍ଲିଖ୍ତ ବୃତ୍ତର ବ୍ୟାସ ।
ମନେକର ଅନ୍ତର୍ଲିଖ୍ତ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ ।
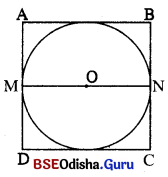
∴ √C = 2r ⇒ r = \(\frac{\sqrt{\mathrm{C}}}{2}\) ଏକକ
∴ଅନ୍ତର୍ଲିଖତ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ \(\frac{\sqrt{C}}{2}\) ଏକକ |
(ii) ଏକ ବୃତ୍ତ ମଧ୍ଯରେ ଗୋଟିଏ ବର୍ଗାକାର କ୍ଷେତ୍ର ଅନ୍ତର୍ଲିଖତ ହେଲେ,
ବର୍ଗକ୍ଷେତ୍ରର କର୍ଷର ଦୈର୍ଘ୍ୟ = ବୃତ୍ତର ବ୍ୟାସ ହେବ ।
ବର୍ଗକ୍ଷେତ୍ରର କଣ୍ଠର ଦୈର୍ଘ୍ୟ = √2 × ବାହୁର ଦୈର୍ଘ୍ୟ = √2 . √C = √2C ଏକକ
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ ହେଲେ, \(\sqrt{2 C}\) = 2r ⇒ r = \(\frac{\sqrt{2 C}}{2}\) = \(\sqrt{\frac{C}{2}}\)
∴ଅନ୍ତର୍ଲିଖତ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ \(\sqrt{\frac{C}{2}}\) ଏକକ |
Question 13.
ପ୍ରମାଣ କର ଗୋଟିଏ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ସହିତ ସମାନ ହେଲେ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଓ ତ୍ରିଭୁଜର ବାହୁର ଦେଶ୍ୟର ଅନୁପାତ \(\sqrt{\frac{\sqrt{3}}{4 \pi}}: 1\) ହେବ ।
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ ହେଲେ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 ବର୍ଗ ଏକକ ହେବ । ସମବାହୁ △ ର ବାହୁର ଦୈର୍ଘ୍ୟ a
ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) a2 ବର୍ଗ ଏକକ ହେବ ।
ପ୍ରଶ୍ନନୁସାରେ, πr2 = \(\frac{\sqrt{3}}{4}\) a2 ⇒ \(\frac{\mathrm{r}^2}{\mathrm{a}^2}\) = \(\frac{\frac{\sqrt{3}}{4}}{\pi}\) ⇒ \(\frac { r }{ a }\) = \(\sqrt{\frac{\sqrt{3}}{4 \pi}}\)
⇒ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ / ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{\sqrt{\frac{\sqrt{3}}{4 \pi}}}{1}\)
∴ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଓ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟର ଅନ୍ମପାଦ \(\sqrt{\frac{\sqrt{3}}{4 \pi}}\) : 1 ହେବ ।
![]()
Question 14.
ଗୋଟିଏ ଅଦ୍ଧବୃତ୍ତାକାର କ୍ଷେତ୍ରର ପରିସୀମା 252 ସେ.ମି. ହେଲେ ଏହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ଅଦ୍ଧବୃତ୍ତାକାର କ୍ଷେତ୍ରର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି. ।
ଅଦ୍ଧବୃତ୍ତାକାର କ୍ଷେତ୍ରର ପରିସୀମା = (πr + 2r) ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, πr + 2r = 252 ⇒ r(\(\frac { 22 }{ 7 }\) + 2) = 252 ⇒ r × \(\frac { 36 }{ 7 }\) = 252
⇒ r = 252 × \(\frac { 7 }{ 36 }\) = 49 ସେ.ମି.
∴ ଅବଦରପାଇ ପେତ୍ରର ପେତ୍ରଫଳ = \(\frac{\pi \mathrm{r}^2}{2}\) ଜି.ମି. = \(\frac { 22 }{ 7 }\) × 49 × 49 × \(\frac { 1 }{ 2 }\) = 3773 ବର୍ଗ ସେ.ମି. ।
Question 15.
ଗୋଟିଏ ଅଦ୍ଧବୃତ୍ତର ପରିସୀମା ବ୍ୟାସ ଅପେକ୍ଷା 44 ମିଟର ଅଧୂକ ହେଲେ ଅର୍ଥବୃତ୍ତାକାର କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ କେତେ ?
Solution:
ମନେକର ଅର୍ଥବୃତ୍ତାକାର କ୍ଷେତ୍ରର ବ୍ୟାସାର୍ଷ = r ମି. ⇒ ଦ୍ୟାସ = 2r ମି. ଓ ପରିସାମା = (πr + 2r) ମି.
ପ୍ରଶ୍ନନୁସାରେ, πr + 2r = 2r + 44
⇒ πr = 44 ⇒ \(\frac { 22 }{ 7 }\) × r = 44 ⇒ r = \(\frac{44 \times 7}{22}\) = 14 ମି.
∴ ଅବଦରପାଇ ପେତ୍ରର ପେତ୍ରଫଳ = \(\frac{\pi \mathrm{r}^2}{2}\) ଜି.ମି. = \(\frac { 22 }{ 7 }\) × 14 × 14 × \(\frac { 1 }{ 2 }\) = 308 ବର୍ଗ ସେ.ମି. ।
Question 16.
ଗୋଟିଏ ଅଦ୍ଧବୃତ୍ତାକାର ପଡ଼ିଆର କ୍ଷେତ୍ରଫଳ 2772 ବର୍ଗମିଟର । ଏହି ପଡ଼ିଆକୁ ବାଡ଼ଦ୍ଵାରା ଆବଦ୍ଧ କରିବାକୁ ହେଲେ ମିଟର ପ୍ରତି 37 ପଇସା ଦରରେ କେତେ ଖର୍ଚ୍ଚ ହେବ ?
Solution:
ମନେକର ଅର୍ଦ୍ଧବୃତ୍ତାକାର ପଡ଼ିଆର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି. ।
ଅର୍ବବୃତ୍ତାକାର ପଡ଼ିଆର କ୍ଷେତ୍ରଫଳ = \(\frac{\pi r^2}{2}\) ବ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{\pi r^2}{2}\) = 2772
⇒\(\frac { 22 }{ 7 }\) × r2 = 2772 × 2 ⇒ r2 = \(\frac{2772 \times 2 \times 7}{22}\)
⇒ r2 = 1764 ⇒ r = 42 ମି.
ଅଦ୍ଧବୃତ୍ତାକାର ପଡ଼ିଆର ପରିସୀମା = (πr + 2r) ମି.
= (\(\frac { 22 }{ 7 }\) × 42 + 2 × 42) ମି.. = (132 + 84) ମି. = 216 ମି.
∴ ପଡ଼ିଆକୁ ବାଡ଼ ଦେବାପାଇଁ ମିଟରକୁ 37 ପଇସା ଖର୍ଚ୍ଚ ହେଲେ 216 ମିଟରକୁ ବାଡ଼ ଦେବାରେ ଖର୍ଚ୍ଚ ହେବ = 216 × 37 ପ. = ଟ. 79.92 |
Question 17.
ଗୋଟିଏ ବୃତ୍ତାକାର ରାସ୍ତାର ବାହାର ଓ ଭିତର ବୃତ୍ତର ବ୍ୟାସ ଯଥାକ୍ରମେ 56 ସେ.ମି. ଓ 42 ସେ.ମି. । ରାସ୍ତାଟିର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ବୃତ୍ତାକାର ରାସ୍ତାର ବାହାର ବୃତ୍ତର ବ୍ୟାସ = 56 ସେ.ମି.
⇒ ବହିଃ ବ୍ୟାସାର୍ଦ୍ଧ (R) = \(\frac { 56 }{ 2 }\) = 28 ସେ.ମି.
ବୃତ୍ତାକାର ରାସ୍ତାର ଭିତର ବୃତ୍ତର ବ୍ୟାସ = 42 ସେ.ମି.
⇒ ଅନ୍ତଃ ବ୍ୟାସାର୍ଦ୍ଧ (r) = \(\frac { 42 }{ 2 }\) = 21 ସେ.ମି.
∴ ରାସ୍ତାର ସେତ୍ରଫଳ = π(R2 – r2)
= \(\frac { 22 }{ 7 }\) (282 – 212) = \(\frac { 22 }{ 7 }\) (784 – 441) = \(\frac { 22 }{ 7 }\) × 343 = 1078 ଟଟ. ସେ.ମି.
![]()
Question 18.
32 ମିଟର ବ୍ୟାସ ବିଶିଷ୍ଟ ଗୋଟିଏ ବୃତ୍ତାକାର ବଗିଚା ମଧ୍ଯରେ ତାହାର ସୀମାକୁ ଲାଗି ଗୋଟିଏ ରାସ୍ତା ନିର୍ମିତ ହୋଇଛି । ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ 352 ବର୍ଗମିଟର ହେଲେ ଏହାର ପ୍ରସ୍ଥ କେତେ ?
Solution:
ରାସ୍ତାର ବାହାର ବୃତ୍ତର ବ୍ୟାସ = 32 ସେ.ମି.
⇒ ବ୍ୟାସାର୍ଦ୍ଧ = OB = \(\frac { 32 }{ 2 }\) = 16 ମି.
ବାହାର କ୍ଷେତ୍ରଫଳ = π × (16)2 ଟ.ମି.
ମନେକର ଅନ୍ତଃବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି.
ଅନ୍ତଃବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = πr2 ବର୍ଗ ମି.
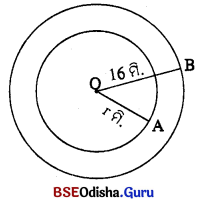
∴ ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ = π(162 – r2) ବର୍ଗ ମି.
ପ୍ରଶ୍ନନୁସାରେ, π(162 – r2) = 352
⇒ \(\frac { 22 }{ 7 }\) (256 – r2) = 352 ⇒ 256 – r2 = 352 × \(\frac { 7 }{ 22 }\)
⇒ 256 – r2 = 112 ⇒ r2 = 144 ⇒ r = 12 ମି. |
∴ ରାସ୍ତାର ପ୍ରମ = (16 – 12) ମି. = 4 ମି. |
Question 19.
ଦୁଇଟି ବୃତ୍ତର ପରିସ୍ର ସମଷ୍ଟି 220 ସେ.ମି. । କ୍ଷେତ୍ରଫଳର ଅନ୍ତର 770 ବର୍ଗ ସେ.ମି. । ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ପ୍ରଥମ ଓ ଦ୍ୱିତୀୟ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ R ସେ.ମି. ଓ r ସେ.ମି. ।
ସେମାନଙ୍କର ପରିସ୍ ଯଥାକ୍ରମେ 2πR ସେ.ମି. ଓ 2πr ସେ.ମି. ।
ସେମାନଙ୍କର କ୍ଷେତ୍ରଫଳ ଯଥାକ୍ରମେ πR2 ବର୍ଗ ସେ.ମି. ଓ πr2 ବର୍ଗ ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, 2лR + 2лг = 220
⇒ 2л (R + r) = 220 ⇒ 2 × \(\frac { 22 }{ 7 }\) (R + r) = 220
⇒ R + r = \(\frac{220 \times 7}{22 \times 2}\) 35 ସେ.ମି. …(i)
ପୁନଶ୍ଚ, лR2 – лr2 = 770 ⇒ л (R2 – r2) = 770
⇒ \(\frac { 22 }{ 7 }\)(R + r) (R – r) = 770
⇒ \(\frac { 22 }{ 7 }\) × 35 (R – r) = 770 ⇒ R – r = \(\frac{770 \times 7}{22 \times 35}\)
⇒ R – r = 7
(i) ଓ (ii) କୁ ଯୋଗକଲେ, 2R = 42 ସେ.ମି. ⇒ R = 21 ସେ.ମି. ଓ r = 35 – 21 = 14 ସେ.ମି.
∴ ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧ 21 ସେ.ମି. ଓ 14 ସେ.ମି. ।
Question 20.
ଗୋଟିଏ ଲୁହା ତାରକୁ ବର୍ଗକୃତି କଲେ ବର୍ଗକ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ 484 ବର୍ଗ ସେ.ମି. ହୁଏ । ଯଦି ଏହାକୁ ବୃତ୍ତାକୃତି କରାଯାଏ ତେବେ ବୃତ୍ତଟିର କ୍ଷେତ୍ରଫଳ କେତେ ହେବ ?
Solution:
ବର୍ଗକ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ = 484 ବର୍ଗ ସେ.ମି.
ବର୍ଗକ୍ଷେତ୍ରଟିର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt{484}\) = 284 ସେ.ମି.
ବର୍ଗକ୍ଷେତ୍ରଟିର ପରିସୀମା = 4 × ବାହୁର ଦୈର୍ଘ୍ୟ = 4 × 22 = 88 ସେ.ମି.
ବୃତ୍ତର ପରିଧ୍ = 88 ସେ.ମି.
ମନେକର ଦରର ବ୍ୟାପାଦ = r ସେ.ମି. ⇒ ବାହୁର ଦୈର୍ଘ୍ୟ = 2πr ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, 2πr = 88
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 88 ⇒ r = \(\frac{88 \times 7}{44}\) = 14 ସେ.ମି.
∴ ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧ = лr2 = \(\frac { 22 }{ 7 }\) × 14 × 14 = 616 ସେ.ମି. |
Question 21.
ଦୁଇଟି ବୃତ୍ତର ବ୍ୟାସର ଅନୁପାତ 4 : 5 । ଯଦି ପ୍ରଥମ ବୃତ୍ତଟିର କ୍ଷେତ୍ରଫଳ 352 ବର୍ଗ ସେ.ମି. କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ବୃତ୍ତର ବ୍ୟାସ = r ଏକକ ହେଲେ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ лr2 ବର୍ଗ ଏକକ
ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସର ଅନୁପାତ 4 : 5 ⇒ ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧର ଅନୁପାତ 4 : 5
∴ ପ୍ରଥମ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 4x ସେ.ମି. ହେଲେ, ଦ୍ୱିତୀୟ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 5x ସେ.ମି. ।
ପ୍ରଥମ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = л × (4x)2 = 16 лx2 ବର୍ଗ ସେ.ମି.
ଦ୍ୱିତୀୟ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = л × (5x)2 = 25 лx2 ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 16лx2 = 352 ⇒ лx2 = \(\frac { 352 }{ 16 }\) = 22
∴ ଦ୍ୱିତୀୟ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = 25 лx2 = 25 × 22 = 550 ବର୍ଗ ସେ.ମି. |
Question 22.
ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ 143√3 ସେ.ମି. ହେଲେ, ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ କେତେ ?
Solution:
ବୃତ୍ତାନ୍ତର୍ଲିଖ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = 14√3 ସେ.ମି.|
ABC ବୃତ୍ତରେ ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ଅନ୍ତର୍ଲିଖୁତ । ପରିବୃତ୍ତର କେନ୍ଦ୍ର O ।
ଆମେ ଜାଣୁ, ସମବାହୁ ତ୍ରିଭୁଜର ଅନ୍ତଃକେନ୍ଦ୍ର, ଭରକେନ୍ଦ୍ର ଓ ଲମ୍ବ ବିନ୍ଦୁ ଏକ ଓ ଅଭିନ୍ନ ଅଟେ ।
O ଭରକେନ୍ଦ୍ର । BO = \(\frac { 2 }{ 3 }\) AD
ପୁନଶ୍ଚ ଉଚ୍ଚତା = AD = 143√3 × \(\frac{\sqrt{3}}{2}\) = 21 ସେ.ମି.|
ବ୍ୟାସାର୍ଦ୍ଧ = BO = \(\frac { 2 }{ 3 }\) AD = \(\frac { 2 }{ 3 }\) × 21 = 14 ସେ.ମି.|
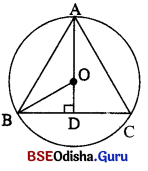
∴ ଦଉର ଯେତ୍ରଫଳ = лr2 = \(\frac { 22 }{ 7 }\) × 14 × 14 = (44 × 14) ଦ.ସେ.ମି. = 616 ଦ.ଗ ସେ.ମି.
△OBD ରେ cos 30° = \(\frac { BD }{ OB }\) ⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{7 \sqrt{3}}{\mathrm{OB}}\)
⇒ OB = 14 ସେ.ମି.|
![]()
Question 23.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ଅନ୍ତଃବୃତ୍ତର କ୍ଷେତ୍ରଫଳ 154 ବର୍ଗ ମି. ହେଲେ, ତ୍ରିଭୁଜର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ଅନ୍ତଃବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି.
ଅନ୍ତଃବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = лr2 ବର୍ଗ ମି.
ପ୍ରଶ୍ନନୁସାରେ, лr2 = 154
⇒ \(\frac { 22 }{ 7 }\) × r2 = 154 ⇒ r2 = 154 × \(\frac { 7 }{ 22 }\) = 49
⇒ r = 7 ମି. = OD
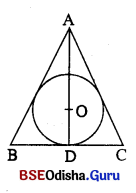
ସମବାହୁ ତ୍ରିଭୁଜର ଅନ୍ତଃକେନ୍ଦ୍ର, ଭରକେନ୍ଦ୍ର ଓ ଲମ୍ବବିନ୍ଦୁ ଏକ ଓ ଅଭିନ୍ନ ଅଟେ ।
∵ O ଉରକେନ୍ଦୁ | AD = 3OD = 3 × 7 = 21 ମି., ରକତା = AD = 21 ମି.
ପଦ୍ରୁର ବୈଶ୍ୟ (AB) = AD × \(\frac{2}{\sqrt{3}}\) = 21 × \(\frac{2}{\sqrt{3}}\) = 14√3 ମି.|
∴ ତ୍ରିକକର ପର୍ବପାପା = 14√3 × 3 = 42√3 ମି.|
Question 24.
ଗୋଟିଏ ବୃତ୍ତରେ ଗୋଟିଏ ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ ଏକ ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟର ତିନିଗୁଣ । ପ୍ରଥମଟିର କ୍ଷେତ୍ରଫଳ ୨ ବର୍ଗ ସେ.ମି. ହେଲେ ଦ୍ବିତୀୟ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ କେତେ ?
Solution:
ମନେକର ଦ୍ୱିତୀୟ ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ L ସେ.ମି. ।
ତେବେ ପ୍ରଥମ ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ 3L ସେ.ମି. ।
ମନେକର ପ୍ରଥମ ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ = r ସେ.ମି.
ପ୍ରଥମ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × 3L × r ⇒ 9 = \(\frac{3 \mathrm{Lr}}{2}\) ⇒ r = \(\frac { 18 }{ 3L }\) = \(\frac { 6 }{ L }\) ସେ.ମି. ।
ଦ୍ୱିତୀୟ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = × Lr = xLx = 3 ବର୍ଗ ସେ.ମି.
(∵ ଦୁଇଟିଯାକ ବୃତ୍ତକଳା, ଗୋଟିଏ ବୃତ୍ତର ଅଟନ୍ତି ।)
∴ ଦ୍ବିତୀୟ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ 3 ବର୍ଗ ସେ.ମି. ।
Question 25.
ଗୋଟିଏ ବୃତ୍ତକଳା ଆକାର ବିଶିଷ୍ଟ କୌଣସି କ୍ଷେତ୍ରର ଚାରିପାଖରେ ବାଡ଼ ଦେବାପାଇଁ ମିଟରକୁ ଟ. 1.50 ହିସାବରେ ଟ. 75 ଖର୍ଚ୍ଚ ହେଲା । ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ 90° ହେଲେ ତାହାର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ?
Solution:
ମିଟରକୁ ଟ. 1.50 ହିସାବରେ 75 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେବ
= \(\frac { 75 }{ 1.50 }\) = \(\frac{75 \times 100}{150}\) ମି. = 50 ନିଗର ଦାଉ ହେବାରେ
ବୃତ୍ତକଳାର ପରିସୀମା = 50 ମିଟର |
ମନେକର ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି. ଓ ଚାପର ଦୈର୍ଘ୍ୟ = l ମି.
ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ (θ) = 90°
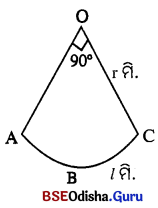
ଚାପର ଦୈର୍ଘ୍ୟ l = \(\frac{\theta}{180^{\circ}}\) × πr
⇒ l = \(\frac { 90 }{ 180 }\) × \(\frac { 22 }{ 7 }\) × r = \(\frac { 11r }{ 7 }\) ମି.
ବୃତ୍ତକଳାର ପରିମାପ = l + 2r = 50 ମି. ⇒ \(\frac { 11r }{ 7 }\) + 2r = 50
⇒ \(\frac{11 r+14 r}{-7}\) = 50 ⇒ 25r = 50 × 7 ⇒ r = \(\frac{50 \times 7}{25}\) = 14 ମି.
ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ 14 ମିଶର |
Question 26.
7 ସେ.ମି. ବ୍ୟାସଦ୍ଧ ବିଶିଷ୍ଟ ତିନୋଟି ବୃତ୍ତ ପରସ୍ପରକୁ ସ୍ପର୍ଶ କରନ୍ତି । ବୃତ୍ତମାନଙ୍କର ବହିଃସ୍ଥ ମାତ୍ର ସେମାନଙ୍କ ଦ୍ଵାରା ଆବଦ୍ଧ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳର ଦଶମିକ ଦୁଇ ସ୍ଥାନ ପର୍ଯ୍ୟନ୍ତ ଆସନ୍ତମାନ ନିର୍ଣ୍ଣୟ କର ।
(√3-1-73, π-3-14)
Solution:
7 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ତିନୋଟି ବୃତ୍ତ ପରସ୍ପରକୁ ଛେଦ କରନ୍ତି ।
ବୃତ୍ତ ତ୍ରୟର ବାହାରେ ଆବଦ୍ଧ କ୍ଷେତ୍ର PQR ଚିହ୍ନିତ ହୋଇଛି ।
ତିନି ବୃତ୍ତର କେନ୍ଦ୍ର A, B, C କୁ ଯୋଗକଲେ ଏକ
ସମବାହୁ ତ୍ରିଭୁଜ ସୃଷ୍ଟି ହେବ;
କାରଣ AB = BC = CA = 2 × 7 = 14 ସେ.ମି. ।
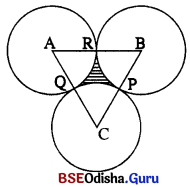
ତେଣୁ △ABC ର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) × (14)2 = \(\frac{\sqrt{3}}{4}\) × 14 × 14 = 49√3 ବର୍ଗ ସେ.ମି. ।
ARQ, BPR, CPQ ତିନି ସମାନ ବୃତ୍ତର ସମାନ ବୃତ୍ତକଳା; ପ୍ରତ୍ୟେକର କୋଣ 60° |
∴ ଆବଦ୍ଧ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = △ABC ର କ୍ଷେତ୍ରଫଳ – ତିନି ସମାନ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳର ସମଷ୍ଟି
= \(\frac{\sqrt{3}}{4}\) × (AB)2 – 76.93 = \(\frac{\sqrt{3}}{4}\) × (14)2 – 76.93 = \(\frac{\sqrt{3}}{4}\) × 196 – 76.93
= 1.73 × 49 – 76.93 = 84.77 – 76.93 = 7.84 ବର୍ଗ ସେ.ମି. ।
![]()
Question 27.
ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ 12 ସେ.ମି. ଓ ବହିଃବ୍ୟାସାର୍ଦ୍ଧ 13 ସେ.ମି. ହୋଇଥିବା ଏକ ବଳୟର କ୍ଷେତ୍ରଫଳ କ୍ଷେତ୍ରଫଳ ସହ ସମାନ ହେଲେ ବୃତ୍ତଟିର ବ୍ୟାସାର୍ଦ୍ଧ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ଏଠାରେ ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ (r) = 12 ସେ.ମି., ବହିଃବ୍ୟାସାର୍ଦ୍ଧ (R) = 13 ସେ.ମି.
∴ ଦଳୀୟର ପ୍ରେତ୍ରଫଳ = π(R2 – r2) = π(132 – 122) = π(13 + 12) (13 – 12) = 25π ଦଶସେ.ମି.
ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି.
ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = лr2 ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, лr2 = 25л ⇒ r2 = 25 ⇒ r = √25 = 5
∴ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = 5 ସେ.ମି.
Question 28.
ଗୋଟିଏ ବୃତ୍ତରେ ଅଙ୍କିତ ଏକ ବୃତ୍ତକଳାର ଚାପ \(\widehat{\mathbf{A X B}}\) ର ଡିଗ୍ରୀ ପରିମାପ 60° । ବ୍ୟାସାର୍ଦ୍ଧ \(\overline{\mathbf{O A}}\),\(\overline{\mathbf{O B}}\) ଏବଂ
\(\widehat{\mathbf{A X B}}\) କୁ ସ୍ପର୍ଶ କରୁଥିବା ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ ୨л ବର୍ଗ ଏକକ ହେଲେ,
(i) ପ୍ରଥମ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ନିର୍ଣ୍ଣୟ କର ।
(ii) OAXB ବୃତ୍ତକଳା ଓ ଏହା ମଧ୍ୟରେ ଅଙ୍କିତ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ ନିର୍ଣ୍ଣୟ କର ।
Solution:
M\(\widehat{\mathbf{A X B}}\) = 60° ⇒ m∠AOB = 60°
ବୃତ୍ତରେ ଅନ୍ତର୍ଲିଖ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = 9л ବର୍ଗ ଏକକ
⇒ лPM2 = 9л ⇒ PM2 = 9 ⇒ PM = 3 ଏକକ
ପ୍ରଥମ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = 3 ଏକକ
OP = 2 PM = 2 × 3 = 6 ଏକକ
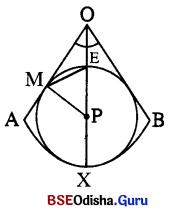
ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ (OX) = OP + PX = OP + PM = 6 + 3 = 9 ଏକକ |
ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { 60° }{ 360 }\) × л(92) = \(\frac { 27л }{ 2 }\) ଏକକ |
∴ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ / ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ = \(\frac{\frac{27}{2} \pi}{9 \pi}\) = \(\frac { 27 }{ 18 }\) = \(\frac { 3 }{ 2 }\) = 3:2
∴ ବୃତ୍ତକଳା ଓ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ = 3 : 2 |
Question 29.
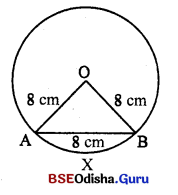
8 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ବୃତ୍ତରେ
(i) 8 ସେ.ମି. ପରିମିତ ଜ୍ୟା ଦ୍ୱାରା ଛେଦିତ କ୍ଷୁଦ୍ରତର ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
(ii) 8√2 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଜ୍ୟା ଦ୍ୱାରା ଛେଦିତ କ୍ଷୁଦ୍ରତର ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
(i) ଏଠାରେ △AOB ସମବାହୁ ।
△AOB ର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) × 82
= 16√3 = 16 × 1.732 = 27.712 ବର୍ଗ ସେ.ମି.
OAXB ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac { θ }{ 360° }\) × лr2 = \(\frac { 60 }{ 360 }\) × 3.141 × 82
= 0.5235 × 64 = 33.504 ବର୍ଗ ସେ.ମି.
∴ କ୍ଷୁଦ୍ରତର ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = (33.504 – 27.712) = 5.792 ବର୍ଗ ସେ.ମି.
(ii) ପାର୍ଶ୍ଵସ୍ଥ ଚିତ୍ରରେ AB = √2 ସେ.ମି., OA = 8 ସେ.ମି., OB = 8 ସେ.ମି.
= △AOB ଏକ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ । ⇒ m∠AOB = 90°
∴ ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = \(\frac { θ }{ 360° }\) × лr2 = \(\frac { 90 }{ 360 }\) × 3.141 × 8 × 8
= 3.141 × 16 = 50.256 ବର୍ଗ ସେ.ମି.
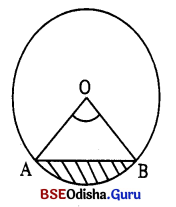
△AOBର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × 8 × 8 = 32 ବର୍ଗ ସେ.ମି.
∴ କ୍ଷୁଦ୍ରତର ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ
= (50.256 – 32) = 18.256 ବର୍ଗ ସେ.ମି.
Question 30.
20 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର କେନ୍ଦ୍ରରେ 60° କୋଣ ଉତ୍ପନ୍ନ କରୁଥିବା ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର । ( √3 − 1.732) (л ~ 3.141)
Solution:
ଏଠାରେ ବ୍ୟାସାର୍ଦ୍ଧ (r) = 20 ସେ.ମି. ଓ କେନ୍ଦ୍ରସ୍ଥ କୋଣ (θ) = 60°
∴ ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = \(\frac { θ }{ 360° }\) × лr2 = \(\frac { 60 }{ 360 }\) × 3.141 × 20 × 20
= 1.047 × 200 = 209.4 ବର୍ଗ ସେ.ମି.
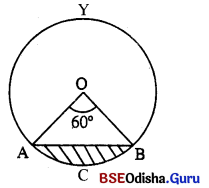
△AOB ର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) × 202 = \(\frac { 1.732 }{ 4 }\) × 400
= 173.2 ବର୍ଗ ସେ.ମି.
∴ କ୍ଷୁଦ୍ରତର ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = (209.4 – 173.2) = 36.2 ବର୍ଗ ସେ.ମି.
∴ ବୃହତ୍ ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ – କ୍ଷୁଦ୍ରତର ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ
= л × (20)2 – 36·2 = 3·141 × 400 – 36·2 = 1256.4 – 36·2 = 1220-2 ବର୍ଗ ସେ.ମି.
Question 31.
10 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର କେନ୍ଦ୍ରରେ 120° କୋଣ ଉତ୍ପନ୍ନ କରୁଥିବା ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର । (3 ~ 1.732) (≈ 3.141)
Solution:
ବ୍ୟାସାର୍ଦ୍ଧ (r) = 10 ସେ.ମି., କେନ୍ଦ୍ରସ୍ଥ କୋଣ (θ) =120°
ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = \(\frac { θ }{ 360° }\) × лr2 = \(\frac { 120 }{ 360 }\) × 3.141 × 10 × 10
= 1.047 × 100 = 104.7 ବର୍ଗ ସେ.ମି.
△AOB ର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) ab sin θ
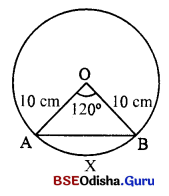
(ଯେଉଁଠାରେ a = b = 10 ସେ.ମି. ଏବଂ θ = 120°)
= \(\frac { 1 }{ 2 }\) × 10 × 10 × sin 120° = \(\frac { 1 }{ 2 }\) × 10 × 10 × \(\frac{\sqrt{3}}{2}\)
= \(\frac{100 \times 1.732}{4}\) = \(\frac { 173.2 }{ 4 }\) = 43.2 ବର୍ଗ ସେ.ମି.
∴ କ୍ଷୁଦ୍ରତର ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = (104.7 – 43.3) = 61.4 ବର୍ଗ ସେ.ମି.
.. ବୃହତ୍ ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ – କ୍ଷୁଦ୍ରତର ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ
= π × 102 – 61.4 = 3.141 × 100 – 61.4 = 314·1 – 61.4 = 252·7 ବର୍ଗ ସେ.ମି.
