BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c)

Question 1.
ଏକ ସରଳ ତ୍ରିଭୁଜାକାର ଭୂମିବିଶିଷ୍ଟ ପ୍ରିଜିମ୍‌ର ଭୂମିର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ a, b, c, ଉଚ୍ଚତା h, ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ L, ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ W ଦ୍ଵାରା ସୂଚିତ ହେଲେ ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନମାନଙ୍କର ସମାଧାନ କର ।
(a) a = 10 ସେ.ମି., b = 6 ସେ.ମି., c = 8 ସେ.ମି., h = 20 ସେ.ମି. କ୍ଷେତ୍ରଫଳ L ଓ W ସ୍ଥିର କର ।
(b) a=5 ମି., b = 5 ମି., c = 6 ମି., h = 8 ମି. ହେଲେ L ଓ W ସ୍ଥିର କର ।
(c) a = b = 15 ମି., c = 24 ମି., b = 18 ମି. ହେଲେ L ଓ W ସ୍ଥିର କର ।
Solution:
ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) = ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା
ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (W) = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) + 2× ଆଧାରର କ୍ଷେତ୍ରଫଳ

(a) △ ର ବାହୁତପର ବୈଶ୍ୟ a = 10 ସେ.ମି., b = 6 ସେ.ମି., ଓ c = 8 ସେ.ମି
ଏଠାରେ 6² + 8² = 10² ତେଣୁ ତ୍ରିଭୁଜଟି ସମକୋଣୀ । ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟ 6 ସେ.ମି 8 ସେ.ମି |
△ ର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × 6 × 8 = 24 ଦଗ ସେ.ମି
△ ର ପରିସାମା = (6 + 8 + 10) ସେ.ମି = 24 ସେ.ମି
∴ ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) = △ ର ପରିସୀମା × ଉଚ୍ଚତା = 24 × 20 = 480 ଦଗ ସେ.ମି
ଏବଂ ପ୍ରିଜିମ୍‌ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (W) = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × △ ର କ୍ଷେତ୍ରଫଳ = 480 + 2 × 24 = 480 + 48 = 528 ଦଗ ସେ.ମି

(b) △ ର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ a = 5 ମି., b = 5 ମି. ଓ c = 6 ମି.
ପ୍ରିଲକର ଅବ ପରିପାପ = s = \(\frac{a+b+c}{2}\) = \(\frac{5+5+6}{2}\) = 8 ମି.
△ ର କ୍ଷେତ୍ରଫଳ = \(\sqrt{8(8-5)(8-5)(8-6)}\)
= \(\sqrt{8 \times 3 \times 3 \times 2}\) = 12 ଦଗ ମି
△ ର ପରିସାମା = (5 + 5 + 6) ମି = 16 ମି.
∴ ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) = △ ର ପରିସୀମା x ଉଚ୍ଚତା = 16 × 8 = 128 ଦଗ ମି
ଏବଂ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (W) = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × △ ର କ୍ଷେତ୍ରଫଳ
= 128 + 2 × 12 = 128 + 24 = 152 ଦଗ ମି

(c) △ ର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ a = 15 ମି., b = 15 ମି.. ଓ c = 24 ମି.
△ ର ପରିସାମା = (15 + 15 + 24) ମି. = 54 ମି.
∴ ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) = △ ର ପରିସୀମା × ଉଚ୍ଚତା = 54 × 18 = 972 ଦଗ ମି
ତ୍ରିୟକର ଅବପରିପାପା = s = \(\frac{a+b+c}{2}\) = \(\frac{15+15+24}{2}\) = 27 ମି.
△ ର କ୍ଷେତ୍ରଫଳ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{27(27-15)(27-15)(27-24)}\)
= \(\sqrt{27 \times 12 \times 12 \times 3}\) = 9 × 12 ଦଗ ମି = 108 ଦଗ ମି
ଏବଂ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (W)
= ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) + 2 × △ ର କ୍ଷେତ୍ରଫଳ
= 972 + 2 × 108 = 972 + 216 ≈ 1188 ଦଗ ମି

Question 2.
ଗୋଟିଏ ପ୍ରିଜିମ୍‌ର ଉଚ୍ଚତା h, ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ L ଏବଂ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ W ଦ୍ଵାରା ସୂଚିତ ହେଲେ ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ସମାଧାନ କର ।
(a) ପ୍ରିଜିମ୍‌ର ଭୂମି ଏକ ସମକୋଣୀ ସମଦିବାହୁ ଯାହାର କର୍ପୂର ଦୈର୍ଘ୍ୟ = 40 ମି, h = 50 ମି, L ଓ W କେତେ ?
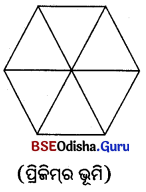
(b) ସୁଷମ ଷଡ଼ଭୁଜାକାର ଆଧାର ବିଶିଷ୍ଟ ଭୂମିର ବାହୁର ଦୈର୍ଘ୍ୟ 6 ଡେ.ମି., h = 20 ସେ.ମି ହେଲେ L ଓ W କେତେ ?
(c) ପିଜିମ୍‌ର ଭୂମି ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ଯାହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 16 ସେ.ମି., h = 25 ସେ.ମି., ହେଲେ L ଓ W କେତେ ? [√3 ≃ 1.732]
Solution:
(a) ପ୍ରିଜିମ୍‌ର ଭୂମି ଏକ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ, ଯାହାର କଣ୍ଣର ଦୈର୍ଘ୍ୟ = 40 ମି.
ତ୍ତିକଲାଭ ବାମନ ବାହାର ଦେଶ୍ୟ = କଣ୍ଡର ଦେଶ୍ୟ / √2 = \(\frac{40}{\sqrt{2}}\) ମି. = 20√2 ମି.
ଆଧାରର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 20√2 × 20√2 = 400 ଦଗ ମି
∴ ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) = ଅଧାରର ପରିସୀମା × ଉଚ୍ଚତା
= 40(√2 + 1) × 50 = 2000 (1.414 + 1)
= 2000 × 2.414 = 4828 ଦଗ ମି
ଓ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (W) = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × △ ର କ୍ଷେତ୍ରଫଳ
= 4828 + 2 × 400 = 5628 ଦଗ ମି |

(b) ପ୍ରିଜିମ୍‌ର ଭୂମି ଏକ ସୁଷମ ଷଡ଼ଭୁଜ ଯାହାର ବାହୁର ଦୈର୍ଘ୍ୟ 6 ସେ.ମି. ।
ପ୍ରିଜିମ୍‌ର ଭୂମି 6 ଗୋଟି ସମବାହୁ △ ରେ ପରିଣତ ହେଲା,
ଯାହାର ବାହୁର ଦୈର୍ଘ୍ୟ = 6 ଡେ.ମି. ।
ଭୂମିର କ୍ଷେତ୍ରଫଳ = 6 × \(\frac{\sqrt{3}}{4}\) × (6)² = 54√3 ବର୍ଗ ଡେ.ମି.
= 54 × 1.732 ଦଗ ମି = 93.528 ବର୍ଗ ଡେ.ମି. |
ଭୂମିର ପରିସୀମା = 6 × 6 = 36 ଡେ.ମି.

∴ ପ୍ରିଜିମ୍ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) = ଭୂମିର ପରିସୀମା × ଉଚ୍ଚତା
ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 36 × 20 = 720 ବର୍ଗ ଡେ.ମି.
ଏବଂ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × ଭୂମିର କ୍ଷେତ୍ରଫଳ
ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = (720 + 2 × 93.528) ବର୍ଗ ଡେ.ମି. = 907.056 ବର୍ଗ ଡେ.ମି.|

(c) ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (L) = ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା = 3 × 16 × 25 = 1200 ବର୍ଗ ଡେ.ମି.
ଆଧାରର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) × (16)²

ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × ଆଧାରର କ୍ଷେତ୍ରଫଳ
= (1200 + 2 × 64 √3) = (1200 + 128 × 1.732)
= (1200 + 221.696) = 1421.696 ବର୍ଗ ଡେ.ମି.|

Question 3.
ଗୋଟିଏ ତ୍ରିଭୁଜାକାର ଭୂମି ବିଶିଷ୍ଟ ସରଳ ପ୍ରିଜିମ୍‌ର ଭୂମିର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 13 ସେ.ମି., ସେ.ମି. ଓ 15 ସେ.ମି. । ଏହାର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 840 ବର୍ଗ ସେ.ମି. ହେଲେ ପ୍ରିଜିମ୍ଟିର ଉଚ୍ଚତା ଓ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ତ୍ରିକାରର ବାହୁତ୍ରୟର ଦୈଶ୍ୟ (a) 13 ସେ.ମି., (b) 14 ସେ.ମି. ଓ (c) 15 ସେ.ମି. |
ତ୍ରିଭୁଜର ଅର୍ଦ୍ଧପରିସୀମା (s) = \(\frac{13+14+15}{2}\) = \(\frac { 42 }{ 2 }\) = 21 ସେ.ମି.
ପ୍ରିଜିମ୍ବର କ୍ଷେତ୍ରଫଳ = \(\sqrt{s(s-a)(s-b)(s-c)}\) = \(\sqrt{21(21-13)(21-14)(21-15)}\)
= \(\sqrt{21 \times 8 \times 7 \times 6}\) = \(\sqrt{3 \times 7 \times 2 \times 2 \times 2 \times 7 \times 3 \times 2}\) = 3 × 7 × 2 × 2 = 84 ବର୍ଗ ସେ.ମି.
ଆଧାରର ପରିପାପା = (13 + 14 + 15) ସେ.ମି. = 42 ସେ.ମି.
ମନେକର ପ୍ରିଜିମ୍ବର ଉଚ୍ଚତା = h ସେ.ମି.
ପ୍ରିଜିମ୍ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରପଳ = ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା = 42h ବର୍ଗ ସେ.ମି.
ପ୍ରମାନୁସାରେ, 42h = 840 ⇒ h = \(\frac { 840 }{ 42 }\) = 20 ସେ.ମି.
∴ ପ୍ରିଜିମୂର ଉଚ୍ଚତା = 20 ସେ.ମି.
∴ ପ୍ରିଜିମ୍‌ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା + 2 × ଆଧାରର କ୍ଷେତ୍ରଫଳ
= 42 × 20 + 2 × 84 = (840 + 168) ର୍ଗ ସେ.ମି. = 1008 ବର୍ଗ ସେ.ମି.

Question 4.
ଗୋଟିଏ ଖୁଣ୍ଟ ଏକ ସମବାହୁ ତ୍ରିଭୁଜାକାର ଭୂମି ବିଶିଷ୍ଟ ସରଳ ପ୍ରିଜିମ୍ । ଏହାର ପାର୍ଶ୍ଵତଳଗୁଡ଼ିକୁ କାଗଜ ମଡ଼ାଇବା ପାଇଁ ପ୍ରତି ବର୍ଗ ସେ.ମି.କୁ 15 ପଇସା ହିସାବରେ ଟ 18.90 ଖର୍ଚ୍ଚ ହେଲା । ଖୁଣ୍ଟଟିର ଉଚ୍ଚତା 8√3 ସେ.ମି. ହେଲେ ଭୂମିର ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
(√3 = 1\(\frac { 3 }{ 4 }\))
Solution:
ପ୍ରିଜିମ୍ ଆକୃତି ବିଶିଷ୍ଟ ସ୍ତମ୍ଭର ପାର୍ଶ୍ଵତଳର କ୍ଷେତ୍ରଫଳ = \(\frac { 18.90 }{ 0.15 }\) = \(\frac { 1890 }{ 15 }\) = 126 ବର୍ଗ ସେ.ମି.
ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରପଳ = ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା
⇒ 126 = ଆଧାରର ପରିସୀମା × 8√3
ଭୂମି ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ହେତୁ ଆଧାରର ପରିସୀମା = 3a (a = ଭୂମିର ବାହୁର ଦୈର୍ଘ୍ୟ)
⇒ 3a = \(\frac{126}{8 \sqrt{3}}\) ⇒ a = \(\frac{126 \times 4}{8 \times 3 \times 7}\) (∵ √3 = \(\frac { 7 }{ 4 }\)) ⇒ a = \(\frac { 504 }{ 168 }\)
∴ ପ୍ରିଜିମ୍‌ର ତ୍ରିଭୁଜାକାର ଭୂମିର ବାହୁର ଦୈର୍ଘ୍ୟ 3 ସେ.ମି. |

Question 5.
18 ମିଟର ଉଚ୍ଚତା ବିଶିଷ୍ଟ ଗୋଟିଏ ତ୍ରିଭୁଜାକାର ଭୂମି ବିଶିଷ୍ଟ ସରଳ ପ୍ରିଜିମ୍‌ର ଭୂମିର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ 12 ମି., 16 ମି. ଓ 20 ମି. ହେଲେ ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ଦେଶ୍ୟ 12 ମି., 16 ମି. ଓ 20 ମି. | ଏଠ।ରେ 12² + 16² = 20²
∴ ତ୍ରିଭୁଜଟି ସମକୋଣୀ । ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 12 ମି. ଓ 16 ମି. ।
∴ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × 12 × 16 = 96 ବର୍ଗ ମି.
ଆଧାରର ପରିସୀମା (12 + 16 +20) ମି. = 48 ମି.
∴ ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ପରିସୀମା × ଉଚ୍ଚତା + 2 × ଭୂମିର କ୍ଷେତ୍ରଫଳ = (48 × 18 + 2 × 96) = 864 + 192 = 1056 ବର୍ଗ ମି. |

Question 6.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 2100 ବ.ସେ.ମି. ଓ ଉଚ୍ଚତା 30 ସେ.ମି. । ଏହାର ଆଧାର ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜ ଯାହାର ବୃହତ୍ତମ ବାହୁର ଦୈର୍ଘ୍ୟ 29 ସେ.ମି. । ଆଧାରର ଅନ୍ୟ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ପ୍ରିଜିମ୍‌ର ଆଧାରର ଅନ୍ୟ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ a ସେ.ମି. ଓ b ସେ.ମି. |
ପ୍ରିଜିମୂର ଆଧାର ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଓ ଏହାର କର୍ପୂର ଦୈର୍ଘ୍ୟ 29 ସେ.ମି. ।
ଏଠ।ରେ a² + b² = 29² ⇒ a² + b² = 841 …(i)
ତ୍ରିଭୁଜର ପରିସୀମା = (a + b + 29) ସେ.ମି.
ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା = (a + b + 29) × 30 ବର୍ଗ ସେ.ମି.
ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର, (a + b + 29) × 30 = 2100 ⇒ a + b + 29 = \(\frac { 2100 }{ 30 }\) = 70
⇒ a + b = 70 – 29 = 41 ⇒ a + b = 41 …(ii)
⇒ (a+b)² = (41)² ⇒ a² + b² + 2ab = 1681
⇒ 841 + 2 ab 1681 (∵ a² + b² = 841)
⇒ 2ab = 1681 – 841 = 840 ⇒ ab = 420
∴ (a – b)² = (a + b)² – 4ab = (41)² – 4 × 420 = 1681 – 1680 = 1
⇒ a – b = 1 ….(iii)
(ii) ଓ (iii)କୁ ଯୋଗକଲେ, 2a = 42 ⇒ a= \(\frac { 2100 }{ 30 }\) = 21 69.
∴ b = 41 — 21 = 20 ସେ.ମି.
∴ ଆଧାରର ଅନ୍ୟ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 21 ସେ.ମି. ଓ 20 ସେ.ମି. ।

Question 7.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍‌ର ଭୂମି ଏକ ସମଙ୍ଗିବାହୁ ତ୍ରିଭୁଜ ଯାହାର ଭୂମିର ଦୈର୍ଘ୍ୟ 24 ସେ.ମି. ଏବଂ ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 13 ସେ.ମି. । ପ୍ରିଜିମ୍ବର ଉଚ୍ଚତା 20 ସେ.ମି. ହେଲେ, ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପ୍ତିକମର କାମି ଏକ ସମବାହୁ ତିକୁଳ |
△ABCର AC = AB 13 ସେ.ମି. ଓ BC = 24 ସେ.ମି. |
\(\overline{\mathrm{AD}}\) ⊥ \(\overline{\mathrm{BC}}\) ବ୍ରେକେ BD = CD = \(\frac { 24 }{ 2 }\) = 12 ସେ.ମି. |

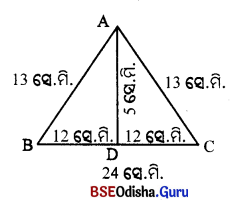
∴ AD = \(\sqrt{13^2-12^2}\) = \(\sqrt{169-144}\) = √25 = 5 ସେ.ମି.
∴ △ABC ର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × 24 × 5 ବର୍ଗ ସେ.ମି. = 60 ବର୍ଗ ସେ.ମି.
∴ ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଅଧାରର ପରିସୀମା × ଉଚ୍ଚତା
= (13 + 13 + 24) × 20 = 50 × 20 = 1000 ବର୍ଗ ସେ.ମି.
∴ ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × △ ର କ୍ଷେତ୍ରଫଳ
= 1000 + 2 × 60 = 1120 ବର୍ଗ ସେ.ମି.

Question 8.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍‌ର ଭୂମି ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । ଯାହାର ବାହୁର ଦୈର୍ଘ୍ୟ 50 ସେ.ମି., ପ୍ରିଜିମ୍‌ର ଉଚ୍ଚତା 1.2 ମି. ହେଲେ, ପ୍ରିଜିମ୍‌ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର । (√3 ≃ 1.732)
Solution:
ପ୍ରିଜିମ୍‌ର ଭୂମି ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = 50 ସେ.ମି. = \(\frac { 1 }{ 2 }\) ମି. ।
ପ୍ରିଜିମ୍‌ର ତ୍ରିଭୁଜ (h) = 1.2 ମି.
ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା
∴ ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 3 × \(\frac { 1 }{ 2 }\) × 1.2 = 1.8 ବର୍ଗ ମି.
ଆଖାଇର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) × (\(\frac { 1 }{ 2 }\))² = \(\frac{\sqrt{3}}{16}\) = \(\frac { 1.732 }{ 16 }\) = 0.10825 ବର୍ଗ ମି.
∴ ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × △ ର କ୍ଷେତ୍ରଫଳ = (1.8 + 2 × 0.10825) = 2.0165 ବର୍ଗ ମି.

Question 9.
ଗୋଟିଏ ତ୍ରିଭୁଜାକାର ଭୂମି ବିଶିଷ୍ଟ ସରଳ ପ୍ରିଜିମ୍‌ର ଭୂମିର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 13 ସେ.ମି., 14 ସେ.ମି. ଓ 15 ସେ.ମି. । ଏହାର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 1050 ବ.ସେ.ମି. ହେଲେ, ପ୍ରିଜିମ୍ବର ଉଚ୍ଚତା ଓ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣୟ କର ।
Solution:
ସରଳ ପ୍ରିଜିମ୍‌ ଆଧାରର ପରିସୀମା = (13 + 14 + 15) ସେ.ମି. = 42 ସେ.ମି. ।
∴ ପ୍ରିକମର ଭକତା = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର / ଆଧାରର ପରିମାପ = \(\frac { 1050 }{ 42 }\) ସେ.ମି. = 25 ସେ.ମି.
ଆଧାରର କ୍ଷେତ୍ରଫଳ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{21(21-13)(21-14)(21-15)}\) (∵ s = \(\frac { 13 + 14 + 15 }{ 2 }\) = 21 ସେ.ମି. )
= \(\sqrt{21 \times 8 \times 7 \times 6}\) = \(\sqrt{7 \times 3 \times 2 \times 2 \times 2 \times 7 \times 2 \times 3}\)
= 7 × 3 × 2 × 2 = 84 ବଗ ସେ.ମି.
∴ ପ୍ରିଜିମ୍‌ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × ଆଧାରର କ୍ଷେତ୍ରଫଳ = (1050 + 2 × 84) = (1050 + 168) = 1218 ବଗ ସେ.ମି.

Question 10.
ଗୋଟିଏ କାଠବାଡ଼ି ଏକ ସମବାହୁ ତ୍ରିଭୁଜାକାର ଭୂମି ବିଶିଷ୍ଟ ସରଳ ପ୍ରିଜିମ୍ । ଏହାର ପାର୍ଶ୍ଵତଳଗୁଡ଼ିକୁ କାଗଜ ମଡ଼ାଇବା ପାଇଁ ପ୍ରତି ବର୍ଗ ସେ.ମି.କୁ 15 ପଇସା ହିସାବରେ ଟ. 18.90 ଖର୍ଚ୍ଚ ହେଲା । କାଠବାଡ଼ିଟିର ଉଚ୍ଚତା 8√3 ସେ.ମି. ହେଲେ, ଭୂମିର ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ? (√3 = 1\(\frac { 3 }{ 4 }\))
Solution:
ପ୍ରିଜିମ୍‌ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = \(\frac { 1890 }{ 15 }\) ବର୍ଗସେ.ମି. = 126 ବଗ ସେ.ମି.
ପ୍ରିଜିମ୍‌ର ଉଚ୍ଚତା = 8√3 = 8 × \(\frac { 7 }{ 4 }\) = 14 ସେ.ମି.
ଆଧାରର ପରିମାପ = ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ / ଉଚ୍ଚତା = \(\frac { 126 }{ 14 }\) ସେ.ମି. = 9 ସେ.ମି.
∴ ଭୂମିର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac { 9 }{ 3 }\) ସେ.ମି. = 3 ସେ.ମି. (∵ ଆଧାର ଏକ ସମବାହ ଚିକକ |)

Question 11.
ଗୋଟିଏ ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ r, ବ୍ୟାସ d ଏବଂ ଉଚ୍ଚତା h ଦ୍ବାରା ସୂଚିତ ହେଲେ ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ସମାଧାନ କର | (π ≃ \(\frac { 22 }{ 7 }\))
(a) d = 16 ସେ.ମି., h = 21 ସେ.ମି. ହେଲେ ମକୁପାରଦତଳର ସ୍ନେତ୍ରଫଳ କେତେ ?
(b) ମକୁପାରଦତଳର ସ୍ନେତ୍ରଫଳ 1188 ବ.ମି., d = 18 ମି. ହେଲେ, h କେତେ ?
(c) ଭୂମିର କ୍ଷେତ୍ରଫଳ 1386 ବ.ସେ.ମି. ଓ h = 36 ସେ.ମି. ହେଲେ, ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ କେତେ ?
Solution:
(a) ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସ (d) = 16 ସେ.ମି., ଉଚ୍ଚତା (h) = 21 ସେ.ମି.
⇒ ବ୍ୟାସାର୍ଦ୍ଧ (r) = \(\frac { 16 }{ 2 }\) = 8 ସେ.ମି.
∴ ସିଲିଣ୍ଡରର ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πrh ବର୍ଗ ସେ.ମି. = 2 × \(\frac { 22 }{ 7 }\) × 8 × 21 ବ. ସେ.ମି. = 1056 ବଗ ସେ.ମି.

(b) ମନେକର ସିଲିଣ୍ଡରର ଉଚ୍ଚତା = h ମି.
ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସ (d) = 18 ମି. ⇒ ବ୍ୟାସାର୍ଦ୍ଧ (r) = \(\frac { 18 }{ 2 }\) = 9 ମି.
∴ ସିଲିଣ୍ଡରର ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରପଳ = 2πrh
= (2 × \(\frac { 22 }{ 7 }\) × 9 × h) ବଗ. ମି. = \(\frac { 396 }{ 7 }\) h ବ.ମି.
ପ୍ରଶାନୁସାରେ, h = 1188 ⇒ h = \(\frac { 1188 × 7 }{ 396 }\) = 21 ମି.
∴ ସିଲିଣ୍ଡରର ଉଚ୍ଚତା 21 ମିଟର ।

(c) ମନେକର ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି. ।
∴ ଭୂମିର କ୍ଷେତ୍ରପଳ = πr² ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, πr² = 1386
⇒ r² = \(\frac { 1386 × 7 }{ 22 }\) = 441 ⇒ r = √441 = 21 ସେ.ମି.
∴ ସିଲିଣ୍ଡରର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πr (h + r)
= 2 × \(\frac { 22 }{ 7 }\) × 21 (36 +21) = 132 × 57 = 7524 ବର୍ଗ ସେ.ମି.

Question 12.
ଗୋଟିଏ ରୋଲର୍‌ର ଦୈର୍ଘ୍ୟ 1.6 ମି. ଏବଂ ଉଚ୍ଚତା 70 ସେ.ମି. । ଏହା କେତେଥର ଘୂରିଲେ 26.4 ଏୟର ସ୍ଥାନ ସମତଳ କରିପାରିବ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ରୋଲର୍‌ର ଦୈର୍ଘ୍ୟ = 1.6 ମି, ଉଚ୍ଚତା = 70 ସେ.ମି. = \(\frac { 70 }{ 100 }\) ମି. = 0.7 ମି.
⇒ ରୋଲର୍‌ର ବ୍ୟାସାର୍ଦ୍ଧ = \(\frac { 1.6 }{ 2 }\) = 0.8 ମି.
∴ ରୋଲର୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πrh = 2 × \(\frac { 22 }{ 7 }\) × 0.8 × 0.7 ବ.ମି. = 3.52 ବ.ମି.
ରୋଲର୍‌ଟି 1 ଥର ଘୂରିଲେ 3.52 ବ.ମି. ସ୍ଥାନ ସମତଳ କରିପାରେ ।
26.4 ଏୟର ବା (26.4 × 100) ବ.ମି. ମାନ ସମତଳ କରିପାରିବ = \(\frac { 26.4 × 100 }{ 3.52 }\) = 750 ଥର ଘୂରିଲେ
∴ ରୋଲର୍‌ଟି 750 ଥର ଘୂରିଲେ 26.4 ଏୟର ସ୍ଥାନ ସମତଳ କରିପାରିବ ।

Question 13.
1540 ବର୍ଗ ମିଟର ଭୂମିରେ ଗୋଟିଏ ରୋଲର 90 ଥର ଗଡ଼ାଇବାକୁ ପଡ଼େ । ରୋଲର୍‌ଟିର ଦୈର୍ଘ୍ୟ ଏହାର ବ୍ୟାସ ସହିତ ସମାନ ହେଲେ ଏହାର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
1540 ବ. ମି. ଭୂମିରେ ଗୋଟିଏ ରୋଲର୍‌ 90 ଥର ଗଡ଼ାଇବାକୁ ପଡ଼େ ।
ରୋଲର୍‌ଟିର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = \(\frac { 1540 }{ 90 }\) = \(\frac { 154 }{ 9 }\) ବର୍ଗ ମି.
ମନେକର ରୋଲର୍‌ର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ = r ମି. | ⇒ ବ୍ୟାସ = 2r ମି. = ରଳତା
∴ ରୋଲର୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 · π · r · (2г) = 4πr² ବ.ମି. [∵ ରଳତା (h) = 2r ମି.]
ପ୍ରଶ୍ନନୁସାରେ,,4πr² = \(\frac { 154 }{ 9 }\) ⇒ r² = \(\frac { 154 }{ 9 }\) × \(\frac { 7 }{ 22 }\) × \(\frac { 1 }{ 4 }\) = \(\frac { 49 }{ 36 }\) ⇒ r = \(\frac { 7 }{ 6 }\) ମି.
∴ ରୋଲର୍‌ର ଦୈର୍ଘ୍ୟ = 2r = 2 × \(\frac { 7 }{ 6 }\) = \(\frac { 7 }{ 3 }\) ମି. = 2\(\frac { 1 }{ 3 }\) ମି.

Question 14.
ଗୋଟିଏ ସିଲିଣ୍ଡର ଆକାର ସ୍ତମ୍ଭର ବଜ୍ରପୃଷ୍ଠତଳକୁ ରଙ୍ଗ କରିବାରେ ପ୍ରତି ବର୍ଗମିଟରକୁ 60 ପଇସା ହିସାବରେ 792 ଟଙ୍କା ଖର୍ଚ ହେଲା । ଏହାର ଭୂମିର କ୍ଷେତ୍ରଫଳ 154 ବର୍ଗମିଟର ହେଲେ ଏହାର ଉଚ୍ଚତା କେତେ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
60 ପଇସା ପ୍ରତି ବର୍ଗମିଟର ବଜ୍ରପୃଷ୍ଠତଳ ରଙ୍ଗ ପାଇଁ ଖର୍ଚ୍ଚ ହେଲେ 792 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେବ = \(\frac { 79200 }{ 60 }\) ବ. 1320 ଦଗମିଟର ଭଳ ପାଇ
ସିଲିଣ୍ଡରର ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 1320 ବର୍ଗମିଟର
ମନେକର ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ = 1 ମି.
ସିଲିଣ୍ଡରର ଭୂମିର କ୍ଷେତ୍ରଫଳ = πr² ବର୍ଗ ମି.
ପ୍ରଶ୍ନନୁସାରେ, πr² = 154
⇒ \(\frac { 22 }{ 7 }\) × r² = 154 ⇒ r² = \(\frac { 154 × 7 }{ 22 }\) = 49 ⇒ r = 7 ମି.
ମନେକର ସିଲିଣ୍ଡରର ଉଚ୍ଚତା = h ମି.
∴ ସିଲିଣ୍ଡରର ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πrh
⇒ 1320 = 2 × \(\frac { 22 }{ 7 }\) × 7 × h ⇒ h = \(\frac { 1320 }{ 2 × 22 }\) = 30 ମି.
∴ ସିଲିଣ୍ଡରର ଉଚ୍ଚତା 30 ମିଟର |

Question 15.
ଗୋଟିଏ ଦୁଇପାଖ ଖୋଲା ଫମ୍ପା ସିଲିଣ୍ଡରର ବହିଃବ୍ୟାସାର୍ଦ୍ଧ 5 ମି. । ଏହାର ଉଚ୍ଚତା 14 ମି. ଏବଂ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 748 ବ.ମି. ହେଲେ, ଏହାର ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ପଣା ସିଲିଣ୍ଡରର ଅନ୍ତଦ୍ୟାପାଦ = r ମି.
ବହିଃବ୍ୟାସାର୍ଦ୍ଧ (R) = 5 ମି., ଉଚ୍ଚତା (h) = 14 ମି.
∴ ଫମ୍ପା ସିଲିଣ୍ଡରର ସମଗ୍ର ସିଲିଣ୍ଡରର କ୍ଷେତ୍ରଫଳ = 2π(R + r)(h + R – r)
= 2 × \(\frac { 22 }{ 7 }\) (5 + r)(14 + 5 – r) ବ.ମି. = \(\frac { 44 }{ 7 }\) (5 + r)(19 – r) ବ. ମି.
ପ୍ରଶ୍ନନୁସାରେ, \(\frac { 44 }{ 7 }\) (5 + r)(19 – r) = 748
⇒ 95 – 5r + 19r – r² = \(\frac { 748 × 7 }{ 44 }\) ⇒ 95 + 14r – r² = 119
⇒ r² – 14r + 24 = 0
⇒ r² – 2r – 12r + 24 = 0 ⇒ r(r – 2) – 12 (r – 2) = 0
⇒ (r – 2) (r – 12) = 0 ⇒ r – 2 = 0 or r – 12 = 0
⇒ r = 2 or 12
∵ ବହିଃବ୍ୟାସାର୍ଦ୍ଧ (R) = 5.ମି. ତେଣୁ ଅନ୍ତରଦ୍ୟାସାଦ (r) = 2 ମି.
∴ ଫମ୍ପା ସିଲିଣ୍ଡରର ଅନ୍ତଦ୍ୟାପାଦ 2 ମିଟର |

Question 16.
ଗୋଟିଏ ଲୁହା ନଳର ଦୈଶ୍ୟ 84 ସେ.ମି. | ଏହାର ବେଧ 2 ସେ.ମି. | ଭୁମିର ବହି ବ୍ୟାପାଇଁ 8 ସେ.ମି ହେଲେ, ସମଣ୍ତତ୍ପ୍ଳର ଯେତ୍ରଫଳ ନିଶଯ କର |
Solution:
ଲୁହାସଲର ଦେଶ୍ୟ (h) = 84 ସେ.ମି. ବହଦ୍ୟାପାଦ (R) = 8 ସେ.ମି. |
ଦେଧ (t) = 2 ସେ.ମି. ⇒ R – r = 2 ⇒ r = R – 2 = 8 – 2 = 6 ସେ.ମି. |
∴ ସମଗପଗଳର ଯେତ୍ରଫଳ = 2π(R + r)(h + t) = 2 × \(\frac { 22 }{ 7 }\) (8 + 6)(84 + 2) ବ. ସେ.ମି.
= 2 × \(\frac { 22 }{ 7 }\) × 14 × 86 ବ. ସେ.ମି. = 7568 ବ. ସେ.ମି.

Question 17.
ଗୋଟିଏ ଲୁହାନଳର ଦୈଶ୍ୟ 100 ସେ.ମି. | ଏବଂ କୁହାଇ ତ୍ପମ 4 ସେ.ମି. | ଏହାର ସମଗପଗଳର ଯେତ୍ରଫଳ 9152 ବ. ସେ.ମି. ହେଲେ ଦୁମିର ସମଣ୍ତତ୍ପ୍ଳର ଓ ଅନ୍ତଦ୍ୟାପାଦ ନିଶ୍ରୟ କର | (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର କୁହାନଳାର ଅନ୍ତଦ୍ୟାପାଦ = r ସେ.ମି.
ଲୁହାନଳର ପ୍ରମ (t) = R – r = 4 ସେ.ମି.
R = (r + 4) ସେ.ମି. ଓ h = 100 ସେ.ମି.
∴ ସମଗପଗଳର ଯେତ୍ରଫଳ = 2π(R + r)(h + t) = 2 × \(\frac { 22 }{ 7 }\) (r + 4 + r)(100 + 4) ବ. ସେ.ମି.
= \(\frac { 44 }{ 7 }\) (2r + 4) × 104 ବ. ସେ.ମି. = \(\frac { 44 }{ 7 }\) × 2(r + 2) × 104 ବ. ସେ.ମି.
= \(\frac { 9152 }{ 7 }\) (r + 2) ବ. ସେ.ମି.
ସମଗପଗଳର \(\frac { 9152 }{ 7 }\) (r + 2) = 9152
⇒ r + 2 = 7 ⇒ r = 7 – 2 = 5
∴ R = r + 4 = 5 + 4 = 9
∴ ଜମିର ବହଦ୍ୟାପାଦ 9 ସେ.ମି. ଓ ଅନ୍ତଦ୍ୟାପାଦ 5 ସେ.ମି. |