Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(b)
Question 1.
ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନମାନଙ୍କ ଉତ୍ତର ସଂକ୍ଷେପରେ ଦିଅ ।
(i) ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମିର ଦୈର୍ଘ୍ୟ = 6 ସେ.ମି. ଓ ଉଚ୍ଚତା = 3 ସେ.ମି., ହେଲେ ଏହାର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମିର ଦୈର୍ଘ୍ୟ = 6 ସେ.ମି. ଓ ଉଚ୍ଚତା = 3 ସେ.ମି. ।
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ଦୈର୍ଘ୍ୟ x ଉଚ୍ଚତା = 6 ସେ.ମି. × 3 ସେ.ମି. = 18 ବର୍ଗ ସେ.ମି. ।
(ii) ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 10 ସେ.ମି. ଓ ଏହାର ସମ୍ମୁଖୀନ କୌଣିକ ବିନ୍ଦୁରୁ କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର
ଦୈର୍ଘ୍ୟ = 6 ସେ.ମି. ହେଲେ, ଏହାର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କଣ୍ଠର ଦୈର୍ଘ୍ୟ = 10 ସେ.ମି.
ଏହାର ସମ୍ମୁଖୀନ କୌଣିକ ବିନ୍ଦୁରୁ କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = 6 ସେ.ମି.
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = କଣ୍ଠର ଦୈର୍ଘ୍ୟ x କଣ୍ଠପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ
= 10 ସେ.ମି × 6 ସେ.ମି = 60 ବର୍ଗ ସେ.ମି. ।
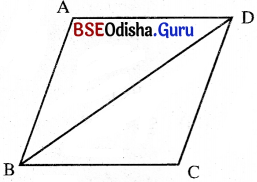
(iii) ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର AB + BD + AD = 2s ଏକକ । s(s – AB) (s – BD) (s – AD) = 64 ହେଲେ, ସାମାନ୍ତରିକ କ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର AB + BD + AD = 2s ଏକକ ।
s(s – AB) (s – BD) (s – AD) = 64
⇒ \(\sqrt{s(s-A B)(s-B D)(s-A D)}=\sqrt{64}\)
⇒ ABD ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = 8 ବର୍ଗ ଏକକ ।
∴ ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 2 × ABD ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ
= 2 × 8 ବର୍ଗ ଏକକ = 16 ବର୍ଗ ଏକକ ।
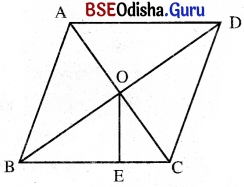
(iv) ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 96 ବର୍ଗ ଏକକ ଓ ଏହାର ଭୂମିର ଦୈର୍ଘ୍ୟ = 8 ଏକକ ହେଲେ, କଣ୍ଠଦ୍ଵୟର ଛେଦବିନ୍ଦୁରୁ ଭୂମିପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 96 ବର୍ଗ ଏକକ ଓ ଭୂମିର ଦୈର୍ଘ୍ୟ BC = 8 ଏକକ
ମନେକର କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁରୁ ଭୂମି ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ O͞E ର ଦୈର୍ଘ୍ୟ = x ଏକକ
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 2 × ଭୂମିର ଦୈର୍ଘ୍ୟ × କର୍ଣ୍ଣଦ୍ଵୟର ଛେଦବିନ୍ଦୁରୁ ଭୂମି ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ
⇒ 96 = 2 × 8 × x
⇒ 96 = 16 × x
⇒ x = \(\frac{96}{16}\) = 6 ଏକକ
∴ କର୍ଣ୍ଣଦ୍ଵୟର ଛେଦବିନ୍ଦୁରୁ ଭୂମିପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 6 ଏକକ ।
(v) ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 144 ବର୍ଗ ଏକକ ଓ ଏହାର ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ 24 ଏକକ ହେଲେ, କର୍ଣ୍ଣର ସମ୍ମୁଖୀନ କୌଣିକ ବିନ୍ଦୁରୁ କଣ୍ଠପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 144 ବର୍ଗ ଏକକ ଏବଂ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 24 ଏକକ
ମନେକର କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = x ଏକକ
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ × କର୍ଣ୍ଣ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ।
⇒ 144 = 24 × x
⇒ x = \(\frac{144}{24}\) = 6 ଏକକ
∴ କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 6 ଏକକ ।
![]()
Question 2.
ଭୂମିର ଦୈର୍ଘ୍ୟ 2.5 ଡେସିମିଟର ଓ ଉଚ୍ଚତା 4.8 ଡେସିମିଟର ବିଶିଷ୍ଟ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
ସମାଧାନ:
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମିର ଦୈର୍ଘ୍ୟ = 2.5 ଡେସି ମି. ଓ ଉଚ୍ଚତା = 4.8 ଡେସି ମି.
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା
= 2.5 × 4.8 ବର୍ଗ ଡ଼େସି ମି. = 12 ବର୍ଗ ଡେସିମିଟର
Question 3.
କୌଣସି ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କଣ୍ଠର ଦୈର୍ଘ୍ୟ 4 ଡେସିମିଟର 6 ସେଣ୍ଟିମିଟର ଏବଂ ଏହି କଣ୍ଠପ୍ରତି ବିପରୀତ କୌଣିକ
ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 22 ସେଣ୍ଟିମିଟର ହେଲେ ଏହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କଣ୍ଠର ଦୈର୍ଘ୍ୟ = 4 ଡେ.ମି. 6 ସେ.ମି. = 46 ସେ.ମି. ଓ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = 22 ସେ.ମି.
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ଦୈର୍ଘ୍ୟ × ଏଥପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ
= (46 x 22) ବର୍ଗ ସେ.ମି. = 1012 ବର୍ଗ ସେ.ମି. ।
Question 4.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 50 ସେ.ମି. ଓ 58 ସେ.ମି. ଏବଂ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 36 ସେ.ମି. ହେଲେ, ଏହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର BD = 50 ସେ.ମି., AC = 58 ସେ.ମି. ଏବଂ AB = 36 ସେ.ମି. ।
A͞C ଓ B͞D କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ଠ ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ।

∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 4 × Δ AOB ର କ୍ଷେତ୍ରଫଳ
= 4 × 360 ବର୍ଗ ସେ.ମି. = 1440 ବର୍ଗ ସେ.ମି. ।
Question 5.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଦୁଇଟି ସନ୍ନିହିତ ବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 26 ମିଟର ଓ 28 ମିଟର ଏବଂ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 30 ମିଟର ହେଲେ, ଏହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ AB = 26 ମି., BC = 28 ମି. ଓ କର୍ଣ୍ଣ AC = 30 ମି. ।
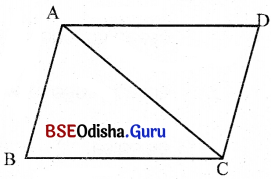

= 2 × 7 × 4 × 3 × 2 × 2 = 672 ବର୍ଗ ସେ.ମି. ।
Question 6.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 24 ସେ.ମି. ଏବଂ ଏହି ବାହୁ ଉପରେ କଣ୍ଠଦ୍ଵୟର ଛେଦବିନ୍ଦୁରୁ ପତିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 10 ସେ.ମି. ହେଲେ, କ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର A͞C ଓ B͞D ପରସ୍ପରକୁ ଠ ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ।
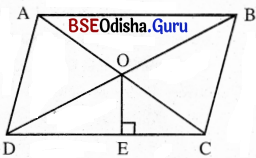
O ବିନ୍ଦୁରୁ C͞D ପ୍ରତି O͞E ଅଙ୍କିତ ଲମ୍ବ ଅଟେ ।
ଦଉ ଅଛି CD = 24 ସେ.ମି. ଏବଂ OE = 10 ସେ.ମି.
∴ Δ COD ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × CD × OE = \(\frac{1}{2}\) × 24 × 10 = 120 ବର୍ଗ ସେ.ମି. ।
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 4 × DOCD ର କ୍ଷେତ୍ରଫଳ = 4 × 120 = 480 ବର୍ଗ ସେ.ମି. ।
![]()
Question 7.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମିର ଦୈର୍ଘ୍ୟ ଓ ଉଚ୍ଚତାର ଅନୁପାତ 2 : 3 ଓ କ୍ଷେତ୍ରଫଳ 726 ବର୍ଗ ସେ.ମି. ହେଲେ, ଭୂମିର ଦୈର୍ଘ୍ୟ ଓ ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମିର ଦୈର୍ଘ୍ୟ = 2x ସେ.ମି. ଓ ଉଚ୍ଚତା = 3x ସେ.ମି. ।
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା = 2x × 3x = 6x2 ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ବାନୁସାରେ, 6x2 = 726 ⇒ x2 = \(\frac{726}{6}\) = 121
⇒ x = \(\sqrt{121}\) = 11 ସେ.ମି. ।
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମିର ଦୈର୍ଘ୍ୟ = 2 × 11 = 22 ସେ.ମି. ଓ ଉଚ୍ଚତା = 3 × 11 = 33 ସେ.ମି. ।
Question 8.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତା ଭୂମିର ଦୈର୍ଘ୍ୟର \(\frac{3}{4}\) ଅଂଶ ଏବଂ କ୍ଷେତ୍ରଫଳ 300 ବର୍ଗମିଟର । କ୍ଷେତ୍ରଟିର ଉଚ୍ଚତା ଓ ଭୂମିର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତା 15 ମିଟର ଓ ଭୂମିର ଦୈର୍ଘ୍ୟ 20 ମିଟର ।
Question 9.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମିର ଦୈର୍ଘ୍ୟ ତା’ର ଉଚ୍ଚତା ଅପେକ୍ଷା 4 ମିଟର ଅଧୂକ । କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 285 ବର୍ଗମିଟର ହେଲେ, ଉଚ୍ଚତା ଓ ଭୂମିର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତା = x ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, ଭୂମିର ଦୈର୍ଘ୍ୟ = (x + 4) ମି. ।
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା
∴ ପ୍ରଶ୍ନନୁସାରେ, x(x + 4) = 285
⇒ x2 + 19x – 15x – 285 = 0
⇒ x2 + 19x – 15x – 285 = 0
⇒ x(x + 19) – 15 (x + 19) = 0
⇒ (x + 19) (x – 15) = 0
⇒ x + 19 = 0 କିମ୍ବା x – 15 = 0
ଯଦି x + 19 = 0 ହୁଏ, ତେବେ x = -19 ଏହା ଅସମ୍ଭବ
∴ x – 15 = 0 ⇒ x = 15 ମି. = ଉଚ୍ଚତା
ଭୂମିର ଦୈର୍ଘ୍ୟ = x + 4 = 15 + 4 = 19 ମି.
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତା 15 ମି. ଏବଂ ଭୂମିର ଦୈର୍ଘ୍ୟ 19 ମି. ।
Question 10.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 420 ବର୍ଗ ସେ.ମି. ଓ ଗୋଟିଏ କୌଣିକ ବିନ୍ଦୁରୁ ଏକ କଳ୍ପ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 14 ସେ.ମି. ହେଲେ, କର୍ପୂର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କର୍ପୂର ଦୈର୍ଘ୍ୟ = x ସେ.ମି. । ଉକ୍ତ କର୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = 14 ସେ.ମି. ।
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ଦୈର୍ଘ୍ୟ × କର୍ଣ୍ଣ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (x × 14) ବର୍ଗ ସେ.ମି. = 14x ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 14x = 420
⇒ x = \(\frac{420}{14}\) = 30 ବର୍ଗ ସେ.ମି.
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 30 ସେ.ମି. ।
Question 11.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଦୁଇଟି ସନ୍ନିହିତ ବାହୁର ଦୈର୍ଘ୍ୟ ଓ କଣ୍ଠର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 25 ମିଟର, 29 ମିଟର ଓ 36 ମିଟର । ଏହି କଣ୍ଠପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
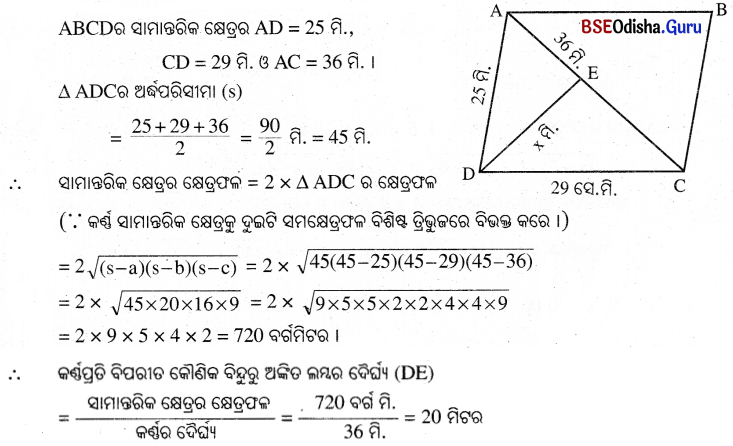
∴ କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣସି ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 20 ମିଟର ।
Question 12.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ,.ଗୋଟିଏ 40 ସେ.ମି. କଣ୍ଠ ବିଶିଷ୍ଟ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ସହ ସମାନ । ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଭୂମିର ଦୈର୍ଘ୍ୟ 40 ସେ.ମି. ହେଲେ, ଏହାର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

![]()
Question 13.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 13 ମିଟର ଏବଂ କ୍ଷେତ୍ରଫଳ 336 ବର୍ଗମିଟର । ଏହାର ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଅପେକ୍ଷା 2 ମିଟର ଅଧିକ ହେଲେ, କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରରେ AB = 13 ମି. ।
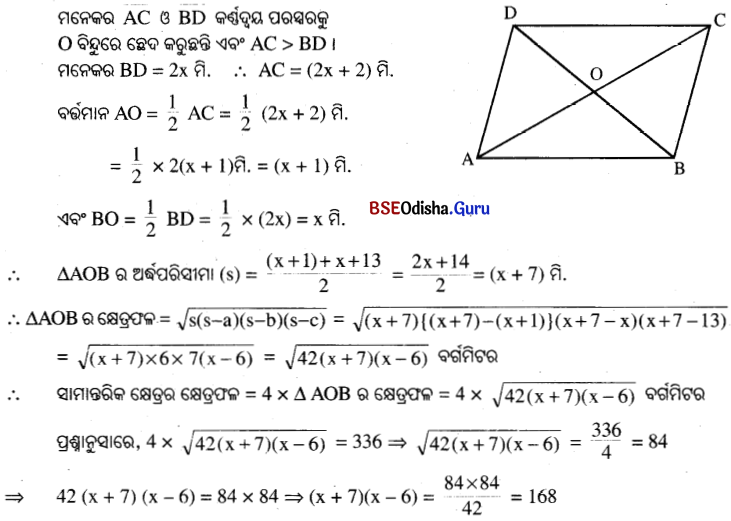
⇒ x2 + 7x – 6x – 42 = 168
⇒ x2 + x – 210 = 0
⇒ x2 + 15x – 14x – 210 = 0
⇒ x(x + 15) – 14 (x + 15) = 0
⇒ (x + 15) (x – 14) = 0
ପ୍ରତି x + 15 = 0 ହୁଏ, x = 15 (ଏହା ଅସମ୍ଭବ) ।
ପ୍ରତି x – 14 = 0 ହୁଏ, ତେଟେ ⇒ x = 14
∴ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x = 2 × 14 = 28 ମିଟର
ଓ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x + 2 = 28 + 2 = 30 ମିଟର ।
Question 14.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ସନ୍ନିହିତ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 16 ସେ.ମି. ଓ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 8 ସେ.ମି. । ଏହାର କ୍ଷେତ୍ରଫଳ 48 ବର୍ଗ ସେ.ମି. ହେଲେ, ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
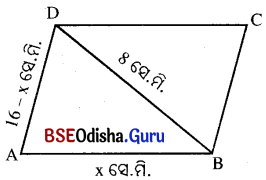
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ AB + AD = 16 ସେ.ମି ।
ଏବଂ କର୍ପୂର ଦୈର୍ଘ୍ୟ BD = 8 ସେ.ମି ।
ମନେକର AB = x ସେ.ମି । ତେବେ AD = (16 – x) ସେ.ମି ।

⇒ 16x – 48 – x2 = 12
⇒ x2 – 16x + 60 = 0
⇒ x2 – 10x – 6x + 60 = 0
⇒ x(x – 10) – 6 (x – 10) = 0
⇒ (x – 10) (x – 6) = 0
⇒ x – 10 = 0 କିମ୍ବା x – 6 = 0
⇒ x = 10 କିମ୍ବା x = 6
ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 10 ସେ.ମି. ହେଲେ ଅନ୍ୟଟି = 16 – x = 16 – 10 = 6 ସେ.ମି. ହେବ ।
ସେହିପରି ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 6 ସେ.ମି. ହେଲେ, ଅନ୍ୟଟି = 16 – x = 16 – 6 = 10 ସେ.ମି. ହେବ ।
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 10 ସେ.ମି. ଓ 6 ସେ.ମି. ।
Question 15.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ସନ୍ନିହିତ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନ୍ତର 8 ମିଟର ଓ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 16 ମିଟର । ଏହାର କ୍ଷେତ୍ରଫଳ 192 ବର୍ଗମିଟର ହେଲେ, ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ AB – AD = 8 ମି. ଏବଂ B͞D କଣ୍ଠର ଦୈର୍ଘ୍ୟ = 16 ମି. ।
ମନେକର AD = x ମି. । ∴ AB = (x + 8) ମି. ।

⇒ x2 + 8x – 240 = 0
⇒ x2 + 20x – 12x – 240 = 0
⇒ x(x + 20) – 12 (x + 20) = 0
⇒ (x + 20) (x − 12) = 0
⇒ x + 20 = 0 or x – 12 = 0
⇒ x = –20 or x = 12.
∴ x = -20 ଏହା ଅସମ୍ଭବ ଏବଂ ହେଲେ x + 8 = 12 + 8 = 20
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 12 ମିଟର ଓ 20 ମିଟର ।
![]()
Question 16.
ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 10 ମିଟର ଓ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 21 ମିଟର ଏବଂ ଏହାର କ୍ଷେତ୍ରଫଳ 168 ବର୍ଗମିଟର । ମିଟରକୁ 12 ଟଙ୍କା ହିସାବରେ ଏହାର ଚାରିପାଖରେ ତାରବାଡ଼ ଦେବାକୁ କେତେ ଖର୍ଜ ଲାଗିବ ?
ସମାଧାନ:
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର BC = 10 ମି., କଣ୍ଠ AC = 21 ମି., B͞E ⊥ A͞C ହେଉ ।
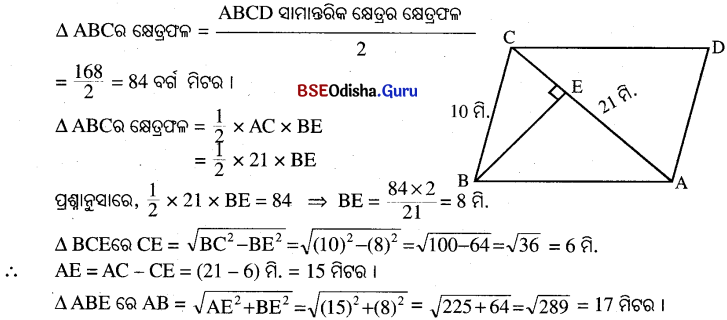
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 2 (AB + BC) = 2 (17+ 10) ମି. = 54 ମି.
1 ମିଟରକୁ 12 ଟଙ୍କା ହିସାବରେ 54 ମିଟରକୁ ବାଡ଼ ଦେବାରେ ଖର୍ଚ୍ଚ ହେବ = 54 × 12 ଟ୍. = 648 ଟଙ୍କା ।
∴ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଚାରିପାଖରେ ବାଡ଼ଦେବାକୁ ମିଟରକୁ 12 ଟଙ୍କା ହିସାବରେ 648 ଟଙ୍କା ଲାଗିବ ।
