BSE Odisha 9th Class Physical Science Solutions Chapter 5 ଗତି

Odisha State Board BSE Odisha 9th Class Physical Science Solutions Chapter 5 ଗତି Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Physical Science Solutions Chapter 5 ଗତି

1. 100 m ପରିଧ ବିଶିଷ୍ଟ ଗୋଟିଏ ବୃତ୍ତାକାର ପଥରେ ଜଣେ ଖେଳାଳୀ 20 ସେକେଣ୍ଡ ସମୟରେ ଥରେ ଘୂରିପାରେ । ତାହାହେଲେ ସେ ଏକ ମିନିଟ୍ 10 ସେକେଣ୍ଡରେ କେତେ ଦୂରତା ଅତିକ୍ରମ କରିବ ଓ ତାହାର ବିସ୍ଥାପନ କେତେ ହେବ ?
ଉ-
ଏଠାରେ ଅତିକ୍ରାନ୍ତ ଦୂରତା (s) = 100 m, ସମୟ (t) = 20 s
∴ ବେଗ (v) =
ଯଦି ସମୟ (t) = 1 ମିନିଟ୍ 10 ସେକେଣ୍ଡ = 70 ସେକେଣ୍ଡ ହୁଏ,
ତେବେ ଅତିକ୍ରାନ୍ତ ଦୂରତା (s) = vt = 5 m/s × 70s = 350 m ହେବ ।
∴ ଖେଳାଳୀ ଜଣକ ମୋଟ 350 m ଦୂରତା ଅତିକ୍ରମ କରିବ ।
ଏଥିରେ ସେ ସଂପୂର୍ଣ୍ଣ 3 ଥର ବୃତ୍ତାକାର ପରିଧ୍ଵକୁ ଏବଂ ଥରେ ଅର୍ଥପରିଧ୍ଵ ପଥ ଅତିକ୍ରମ କରିବ ।
ତେଣୁ ତାହାର ବିସ୍ଥାପନ = ବୃତ୍ତର ପରିଧ୍ଵ
∴ ବୃତ୍ତର ପରିଧ୍ଵ = πd = 100 m (∵ d = ବୃତ୍ତର ବ୍ୟାସ)

ଖେଳାଳୀର ବିସ୍ଥାପନ 31.818m ମିଟର ହେବ ।

2. ସୁମନ୍ତ ବିଦ୍ୟାଳୟକୁ ଗଲାବେଳେ 20 km/h ବେଗରେ ଗାଡ଼ିରେ ଯାଏ । ବିଦ୍ୟାଳୟରୁ ଫେରିଲାବେଳେ ତାହାର ଗାଡ଼ିର ବେଗ 30 km/h ହେଲେ, ତାହାର ହାରାହାରି ବେଗ କେତେ ହେବ ?
ଉ-
ମନେକର ସୁମନ୍ତ ଘରଠାରୁ ବିଦ୍ୟାଳୟର ଦୂରତ୍ୱ = x km
x kmକୁ 20 km/h ବେଗରେ ବିଦ୍ୟାଳୟ ଯିବାକୁ ସମୟ ଲାଗିବ =

∴ ସୁମନ୍ତର ହାରାହାରି ବେଗ 24 km/h ।

3. ଏକ ମୋଟର ବୋଟ୍ ସ୍ଥିରାବସ୍ଥାରୁ ଗୋଟିଏ ହ୍ରଦରେ ଏକ ସରଳରେଖାରେ ଗତିକଲା । 8 ସେକେଣ୍ଡ ସମୟରେ ତାହାର ତ୍ଵରଣ 3 m/s² ହେଲା । ଏହି ସମୟ ମଧ୍ୟରେ ବୋଟ୍‌ କେତେ ଦୂରତା ଅତିକ୍ରମ କରିଥିଲା ?
ଉ-
ଏଠାରେ ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) = 0, ସମୟ (t) = 8 s ଓ ତ୍ଵରଣ (a) = 3m/s²
∴ ଅତିକ୍ରାନ୍ତ ଦୂରତା
∴ ବୋଟ୍‌ଟି 96 ମି. ଦୂରତା ଅତିକ୍ରମ କରିଥିଲା ।

4. ରାମବାବୁ ସକାଳୁ ଘରୁ ବାହାରି ପୂର୍ବ ଦିଗକୁ 2 km ଗଲେ ଏବଂ ସେଠାରୁ ସେଇବାଟ ଦେଇ ଘରକୁ ଫେରି ଆସିଲେ । ଏହି ଦୂରତା ଅତିକ୍ରମ କରିବାକୁ ସେ ମୋଟ 40 ମିନିଟ୍ ସମୟ ନେଇଥୁଲେ, ତାଙ୍କର ହାରାହାରି ବେଗ ଓ ପରିବେଗ କଳନା କର ।
ଉ –

ରାମବାବୁଙ୍କର ହାରାହାରି ବେଗ 6 km/h ଓ ବିସ୍ଥାପନ 0 |

5. ଚିତ୍ରରେ ତିନୋଟି ଗାଡ଼ି A, B ଓ Cର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ପ୍ରଦର୍ଶିତ ହୋଇଛି । ଏହି ଗ୍ରାଫ୍‌କୁ ଅନୁଧ୍ୟାନ କରି ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଲେଖ ।
(a) ଏମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ ଗାଡ଼ିଟିର ଗତି ସର୍ବାଧ୍ବକ ?
(b) ରାସ୍ତାର କୌଣସି ଗୋଟିଏ ସ୍ଥାନରେ ସେମାନେ ଏକାଠି ହେବେ କି ?
(c) B ଗାଡ଼ିଟି A ଗାଡ଼ିକୁ ଅତିକ୍ରମ କରିବା ପରେ c ଗାଡ଼ିଟି କେତେ ଦୂର ଯାଇଥ‌ିବ ?
(d) C ଗାଡ଼ିକୁ ଅତିକ୍ରମ କରିବା ପରେ B ଗାଡ଼ିଟି କେତେ ଦୂର ଯାଇଥିବ ?

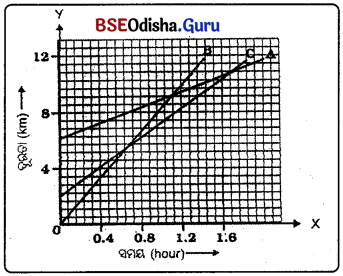
ଉ –

(a) ଗତି ଶୀଳ ବସ୍ତୁର ବେଗର ପରି ମାଣ ଦୂରତ। -ସମୟ ଗ୍ରାଫ୍‌ ଆନତି (Slope)ରୁ ଜଣାପଡ଼ିଥାଏ । Bର ଲେଖାଟି X-ଅକ୍ଷ ବା ସମୟ ଅକ୍ଷ ସହ ଉତ୍ପନ୍ନ କରୁଥ‌ିବ। କୋଣର ପରିମାଣ ଅଧିକ ହୋଇଥିବାରୁ ତ’ର ସ୍ଲୋପ୍ ଅଧିକ ହୋଇଥାଏ । ସୁତରାଂ Bର ବେଗ ସର୍ବାଧ‌ିକ ଅଟେ ।

(b) ରାସ୍ତାର କୌଣସି ସ୍ଥାନରେ ସେମାନେ ଏକାଠି ହେବେ ନାହିଁ ।

(c) B ଗାଡ଼ିଟି A ଗାଡ଼ିକୁ D ଠାରେ ଅତିକ୍ରମ କରୁଛି । D ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ Y -ଅକ୍ଷରେ 10 km । ସେହି ସମୟରେ ୯ ଗାଡି E ଠାରେ ପହଞ୍ଚିବ ଏବଂ E ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ Y-ଅକ୍ଷରେ 9km । ତେଣୁ B, Aକୁ ଅତିକ୍ରମ କଲାବେଳେ ୯ ଗାଡି B ଓ A ଠାରୁ (10 km – 9 km) = 1 km ପଛରେ ଥ‌ିବ ।

(d) B ଗାଡି C ଗାଡିକୁ F ଠାରେ ଅତିକ୍ରମ କରୁଛି ଏବଂ F ର ସ୍ଥାନାଙ୍କ Y-ଅକ୍ଷରେ 7.5 km 1 B, Cକୁ ମୂଳବିନ୍ଦୁଠାରୁ 7.5 km ଦୂରରେ ଏବଂ A କୁ ମୂଳବିନ୍ଦୁଠାରୁ 10 km ଦୂରରେ ଅତିକ୍ରମ କରିବ । ତେଣୁ B ଗାଡି ୯ ଗାଡିକୁ ଅତିକ୍ରମ କରିବା ସୟରେ (10 km – 7.5 km) = 2.5 km ଦୂରତା ଅତିକ୍ରମ କରିବ ।

6. ଗୋଟିଏ ବସ୍ତୁ ଭୂମିଠାରୁ 20 m ଉପରୁ ସ୍ଥିରାବସ୍ଥାରୁ ମୁକ୍ତ ଭାବରେ ପଡ଼ିଲା । ଭୂପୃଷ୍ଠରେ ପଡ଼ିବାକୁ ଏହାକୁ କେତେ ସମୟ ଲାଗିବ ? ଠିକ୍ ଭୂମିକୁ ଛୁଇଁବା ବେଳେ ଏହାର ପରିବେଗ କେତେ ହେବ ?(g = 10 m/s²)
ଉ –
ଏଠାରେ ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) ), ଭୂମିଠାରୁ ବସ୍ତୁର ଉଚ୍ଚତା (s) = 20m
ଓ ମାଧ୍ୟାକର୍ଷଣ ଜନିତ ତ୍ଵରଣ (g) = 10 m/s²
v² = u² + 2gs = 2gs (∵ u = 0)

v = u + gt ⇒ t =
∴ ଭୂପୃଷ୍ଠରେ ପଡ଼ିବାକୁ 2 ସେକେଣ୍ଡ ସମୟ ଲାଗିବ ଓ ଠିକ୍ ଭୂମିରେ ଛୁଇଁବା ବେଳେ ଏହାର ପରିବେଗ 20m/s ହେବ ।

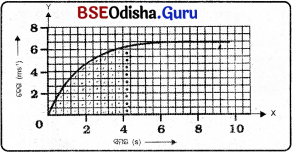
7. ଗ୍ରାଫ୍ ପ୍ରଦର୍ଶିତ ହୋଇଛି । ଏହାକୁ ପର୍ଯ୍ୟବେକ୍ଷଣ କର ଏବଂ ନିମ୍ନୋକ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଲେଖ ।

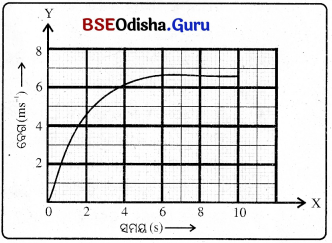
(a) ପ୍ରଥମ ଚାରି ସେକେଣ୍ଡରେ କାର୍‌ଟି କେତେ ଦୂରତା ଅତିକ୍ରମ କରିବ ? ଏହି ସମୟରେ କାର୍‌ଟି ଅତିକ୍ରମ କରିଥୁବା ଦୂରତା ପ୍ରଦର୍ଶନ କରୁଥିବା ଗ୍ରାଫ୍‌ର ଅଂଶକୁ ରଙ୍ଗ ଦିଅ ।
(b) ଗ୍ରାଫ୍‌ରେ କେଉଁ ଅଂଶଟିର କାର୍‌ଟି ସମ ଗତିରେ ଗତି କରୁଛି ?
ଉ –
(a) V = 6 m/s, t = 4s
s = vt = 6m/s x 4s = 24m
ଗ୍ରାଫ୍‌ତ ରେଖାଙ୍କିତ ଅଂଶ ହେଉଛି କାର୍ ଟି ଅତିକ୍ରମ କରୁଥିବା ଦୂରତା ।
(b) ଗ୍ରାଫ୍‌ରେ 6 ସେକେଣ୍ଡରୁ 9.6 ସେକେଣ୍ଡ ମଧ୍ୟରେ

8. ଗୋଟିଏ ବସ୍ତୁକୁ ଭୂଲମ୍ବ ଦିଗରେ ଭୂମିଠାରୁ ଉପରକୁ ନିକ୍ଷେପ କରାଗଲା । ଏହା 4 ସେକେଣ୍ଡ ପରେ ପ୍ରାରମ୍ଭିକ ସ୍ଥାନକୁ (ଯେଉଁ ସ୍ଥାନରୁ ଯାଇଥିଲା ସେହି ସ୍ଥାନକୁ) ଫେରି ଆସିଲା । ତାହାହେଲେ ଏହାର ପ୍ରାରମ୍ଭିକ ବେଗ କେତେ ଥିଲା ? ଏହା କେତେ ଉପରକୁ ଉଠିଥିଲା ? (g = 10 m/s²)
ଉ –
ପ୍ରାରମ୍ଭିକ ବେଗ = u; ଅନ୍ତିମ ବେଗ v = 0; ମୋଟ ସମୟ ଲାଗିଛି t = 4 sec
କେବଳ ଉପରକୁ ଉଠିବାକୁ ସମୟ ଲାଗିଛି  
(ଉପରକୁ ଉଠିବାକୁ ଯେତିକି ସମୟ ଲାଗିବ ତଳକୁ ଖସିବାକୁ ସେତିକି ସମୟ ଲାଗିବ ।)
ଉପରକୁ ଉଠିବାପାଇଁ v = 0, t = 2 sec. g = – 10 m/s²
v = u + gt ⇒ 0 = u + gt ⇒ u = – gt = – (- 10m/s²) x 2s = 20 m/s
v² = u² + 2 gs ⇒ 0 = u² + 2 gs

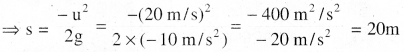
∴ ବସ୍ତୁଟି 20m ଉପରକୁ ଉଠିଥିଲା ଓ ତାହାର ପ୍ରାରମ୍ଭିକ ବେଗ 20 m/s ଥିଲା ।

9. ଗୋଟିଏ କୃତ୍ରିମ ଉପଗ୍ରହ 42250 km ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତାକାର କକ୍ଷରେ ପୃଥ‌ିବୀ ପରିକ୍ରମଣ କରୁଅଛି । ଯଦି ଏହା ପୃଥ‌ିବୀ ଚାରିପାଖରେ 24 ଘଣ୍ଟାରେ ଥରେ ଘୂରିଆସେ, ତାହାହେଲେ ଏହାର ବେଗ
ଉ –
ଏଠାରେ ବ୍ୟାସାର୍ଷ (r) = 42250 km, ସମୟ (t) = 24 h
⇒ ଅତିକ୍ରାନ୍ତ ଦୂରତା (s) = ପରିଧ୍ 2лr = 2 x 3.141 x 42250 km = 265414.5 km

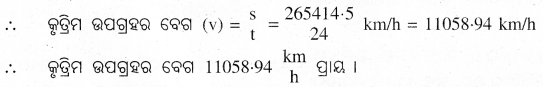
10. ସ୍ଥିରାବସ୍ଥାରୁ ଗୋଟିଏ କାର୍ ଗତି ଆରମ୍ଭ କରି ଏକ ସିଧା ରାସ୍ତାରେ 4 m/s² ସମ ତ୍ଵରଣରେ ଗତି କଲା । 10 ସେକେଣ୍ଡ ପରେ ଏହାର ପରିବେଗ କେତେ ହେବ ? ଏହି ସମୟ ମଧ୍ୟରେ କାର୍‌ଟି କେତେ ଦୂର ଯାଇଥ‌ିବ ?
ଉ –
ଏଠାରେ ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) = 0, ତ୍ଵରଣ (a) = 4 m/s² ଓ ସମୟ (t) = 10s
ଅନ୍ତିମ ପରିବେଖ = v ହେଲେ v = u + at = 0 + 4 m/s² x 10s = 40 m/s
ଅତିକ୍ରାନ୍ତ ଦୂରତା
∴ 10 ସେକେଣ୍ଡ ପରେ କାର୍‌ର ପରିବେଗ ହେବ 40 m/s । ଏହି ସମୟ ମଧ୍ୟରେ କାର୍‌ଟି 200 m ଦୂର ଯାଇଥ‌ିବ ।

ପ୍ରଶାବଳୀ ଓ ଉତ୍ତର

1. ଗୋଟିଏ ବସ୍ତୁ କିଛି ପଥ ଦେଇ ଗତି କରିଛି । ତାହାର ବିସ୍ଥାପନ ଶୂନ ହୋଇ ପାରିବ କି ? ଯଦି ତୁମର ଉତ୍ତର ହଁ ହୁଏ, ତାହାହେଲେ ଏକ ଉଦାହରଣ ଦ୍ଵାରା ଏହାକୁ ବୁଝାଅ ।
ଉ –
(i) ବସ୍ତୁର ବିସ୍ଥାପନ ଶୂନ ହୋଇପାରିବ ।

(ii) ଉଦାହରଣ : 1 – ଗୋଟିଏ ବସ୍ତୁ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁ ‘A’ ରୁ ବାହାରି କୌଣସି ଏକ ପଥ ଅତ୍ରିକମ କରି ପୁନଶ୍ଚ ସେହି ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁ ‘A’ କୁ ଫେରିଆସିଲେ ବସ୍ତୁର ବିସ୍ଥାପନ ଶୂନ ହେବ । କାରଣ ପ୍ରାରମ୍ଭିକ – ବିନ୍ଦୁ ଓ ଅନ୍ତିମ ବିନ୍ଦୁ ମଧ୍ୟରେ ସର୍ବନିମ୍ନ ଦୂରତା ସମାନ ଅଟେ ।

ଉଦାହରଣ : 2 – ମନେକର, ଗୋଟିଏ ବସ୍ତୁ ‘୦’ ବିନ୍ଦୁରୁ ବାହାରି A ପର୍ଯ୍ୟନ୍ତ ଏକ ସରଳରେଖାରେ ଯାଇ ପୁନଶ୍ଚ ‘୦’ ବିନ୍ଦୁକୁ ଫେରିଆସିଲା । ଏ କ୍ଷେତ୍ରରେ ବସ୍ତୁର ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁ ଓ ଅନ୍ତିମ ବିନ୍ଦୁ ସମାନ ହୋଇଯିବାରୁ ବସ୍ତୁର ବିସ୍ଥାପନ ଶୂନ ହେବ ।
∴ \(\vec{OA}\) = – \(\vec{OA}\) କିମ୍ବା \(\vec{OA}\) + \(\vec{OA}\) = 0 (\(\vec{OA}\) ଯୁକ୍ତାତ୍ମକ ହେଲେ \(\vec{OA}\) ବିଯୁକ୍ତାତ୍ମକ ହୋଇଥାଏ । )

ଉଦାହରଣ : 3 – ଗୋଟିଏ ଟେକାକୁ ଭୁଲମ୍ବ ଭାବରେ ଉପରକୁ ନିକ୍ଷେପ କଲେ ତାହା କିଛି ବାଟ ଉପରକୁ ଯାଇ କିଛି ସମୟ ପରେ ପ୍ରାରମ୍ଭିକ ଅବସ୍ଥାନକୁ ଫେରିଆସେ । ଏଠାରେ ଟେକାର ବିସ୍ଥାପନ ଶୂନ ମାତ୍ର ଅତିକ୍ରାନ୍ତ ଦୂରତା ଶୂନ ହୋଇନଥାଏ ।

2. ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଠିକ୍ ଓ କେଉଁଟି ଭୁଲ ପ୍ରକାଶ କର ।
(a) ବିସ୍ଥାପନ କେବେହେଲେ ଶୂନ ହେବନାହିଁ ।
(b) ବିସ୍ଥାପନର ପରିମାଣ ଅତିକ୍ରାନ୍ତ ଦୂରତାର ପରିମାଣଠରୁ କେବେହେଲେ ଅଧିକ ହେବ ନାହିଁ ।
ଉ –
(a) ଭୁଲ
(b) ଠିକ୍ ।

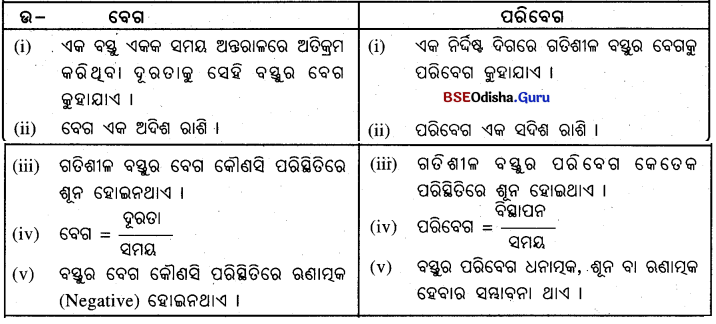
3. ବେଗ ଓ ପରିବେଗ ମଧ୍ଯରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
ଉ –

4. କେଉଁ ପରିସ୍ଥିତିରେ ହାରାହାରି ପରିବେଗର ପରିମାଣ ହାରାହାରି ବେଗ ସହ ସମାନ ?
ଉ –
ବସ୍ତୁଟି ଏକ ସରଳରେଖାରେ ଏବଂ ସମ ପରିବେଗରେ ଗତି କରୁଥିଲେ ଏହାର ହାରାହାରି ପରିବେଗର ପରିମାଣ ହାରାହାରି ବେଗ ସହ ସମାନ ହେବ ।

5. ଗୋଟିଏ ଯାନର ‘‘ଓଡ଼ୋମିଟର’’ ଯନ୍ତ୍ର କ’ଣ ମାପେ ?
ଉ –
ଗୋଟିଏ ଯାନର ଓଡ଼ୋମିଟର ଯନ୍ତ୍ର ବସ୍ତୁର ଅତିକ୍ରାନ୍ତ ଦୂରତା ମାପେ ।

6. ଯେତେବେଳେ ଗୋଟିଏ ବସ୍ତୁ ସମଗତିରେ ଗତି କରୁଥାଏ, ତାହାର ଗତିପଥ କିପରି ହୋଇଥାଏ ?
ଉ –
ଯେତେବେଳେ ଗୋଟିଏ ବସ୍ତୁ ସମଗତିରେ ଗତି କରୁଥାଏ, ସେତେବେଳେ ତାହାର ଗତିପଥ ସରଳରେଖକ ହୋଇଥାଏ ।

7. ଗୋଟିଏ ବସ୍ତୁ

• କେତେବେଳେ ସମ ତ୍ଵରଣରେ ଯାଉଛି ବୋଲି ତୁମେ କହିବ ଏବଂ
• କେତେବେଳେ ଅସମ ତ୍ଵରଣରେ ଯାଉଛି ବୋଲି ତୁମେ କହିବ ।

ଉ –

• ଯଦି ବସ୍ତୁ ଏକ ସରଳରେଖାରେ ଗତି କରୁଥିବା ସମୟରେ ତାହାର ପରିବେଗ ସମାନ ସମୟ ବ୍ୟବଧାନରେ ସମାନ ପରିମାଣରେ ବୃଦ୍ଧି ଘଟିଥାଏ, ତେବେ ତାହା ସମ ତ୍ଵରଣରେ ଯାଉଛି ବୋଲି କୁହାଯାଏ ।
• ସେହିପରି ଯଦି ସଳଖ ରାସ୍ତାରେ ଗୋଟିଏ ଗତିଶୀଳ ବସ୍ତର ବେଗ ଅସମାନଭାବରେ ସମାନ ସମୟ ବ୍ୟବଧାନରେ ବୃଦ୍ଧିପାଏ, ତେବେ ତାହା ଅସମ ତ୍ଵରଣରେ ଯାଉଛି ବୋଲି କୁହାଯିବ ।

8. ସରଳରେଖାରେ ଗୋଟିଏ ବସ୍ ତାହାର ପରିବେଗ 80 km/hରୁ 60 km/h କୁ 5 ସେକେଣ୍ଡରେ କମାଇଲା । ତାହାହେଲେ ସେ ବସ୍‌ର ଗତିରେ ତ୍ଵରଣ କେତେ ?
ଉ –

9. ଗୋଟିଏ ଟ୍ରେନ୍ ରେଳଷ୍ଟେସନରୁ ଛାଡ଼ି ସମ ତ୍ଵରଣରେ ଗତିକରି 10 ମିନିଟ୍‌ରେ 40 km/h ପରିବେଗ ଲାଭକଲେ, ଟ୍ରେନ୍‌ର ତ୍ଵରଣ କେତେ ?
ଉ –
ଟ୍ରେନ୍ ର ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) = 0
ଅନ୍ତିମ ପରିବେଗ (v) = 40 କି.ମି./ ଘଣ୍ଟା ମି. / ସେକେଣ୍ଡ = \(\frac { 100 }{ 9 }\) ମି. / ସେକେଣ୍ଡ
ସମୟ (t) = 10 ମିନିଟ୍ = 10 × 60 606 = 600 ସେକେଣ୍ଡ
ତ୍ଵରଣ (a) = \(\frac { v-u }{ t }\) = \(\frac { v }{ t }\) = \(\frac { 100 }{ 9 x 600 }\) ମିଟର / ସେକେଣ୍ଡ
= ମିଟର / ସେକେଣ୍ଡ² = 0.018 ମିଟର / ସେକେଣ୍ଡ²
∴ ଟ୍ରେନ୍‌ର ତ୍ଵରଣ 0.018 ମିଟର / ସେକେଣ୍ଡ²

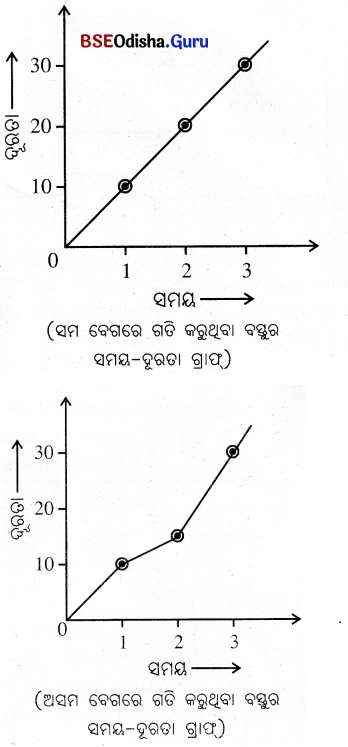
10. ସମ ଓ ଅସମ ବେଗରେ ଗତି କରୁଥିବା ଗୋଟିଏ ବସ୍ତୁର ସମୟ–ଦୂରତା ଗ୍ରାଫ୍‌ର ଲକ୍ଷଣଗୁଡ଼ିକ ଲେଖ ।
ଉ –

• ସମ ବେଗରେ ଗତି କରୁଥିବା ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍‌ ଏକ ତୀର୍ଯ୍ୟକ୍ ସରଳରେଖା ହୁଏ ।
• ବସ୍ତୁଟି ଅସମ ବେଗରେ ଗତି କରୁଥିଲେ ଗ୍ରାଫ୍‌ଟି ଏକ ବକ୍ରରେଖା ହୁଏ ।

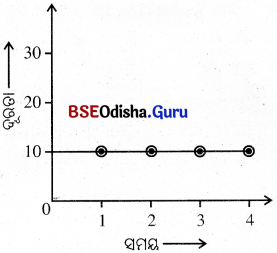
11. ଗୋଟିଏ ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ସମୟ ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇଥିଲେ, ତାହାର ଗତି କ’ଣ ହୋଇପାରେ ବୋଲି ତୁମେ ଭାବୁଛ ?
ଉ –
ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ସମୟ ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇଥିଲେ ବସ୍ତୁଟି ସ୍ଥିର ଖୁବ। ଜଣାଯାଏ ।

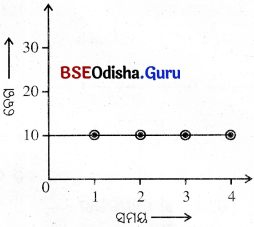
12. ଗୋଟିଏ ବସ୍ତୁର ସମୟ-ବେଗ ଗ୍ରାଫ୍ ଏକ ସରଳରେଖା ଏବଂ ଏହା ସମୟ ଅକ୍ଷ ସହ ସମାନ୍ତ ର । ବସ୍ତୁର ଗତି ବିଷୟରେ ତୁମେ କ’ଣ କହିପାରିବ ?
ଉ –
ଗୋଟିଏ ସମୟ-ବେଗ ଗ୍ରାଫ୍ ଏକ ସରଳରେଖା ଏବଂ ସମୟ ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇଥିଲେ ବସ୍ତୁଟି ସମବେଗରେ ଗତି କରିବ ।

13. ଗୋଟିଏ ବସ୍ ସ୍ଥିରାବସ୍ଥାରୁ ଗତି ଆରମ୍ଭ କରି 2 ମିନିଟ୍‌ରେ 0-1 m/s² ତ୍ଵରଣ ଲାଭ କଲା । ତାହାହେଲେ–

• ଏହି ସମୟ ମଧ୍ୟରେ ବସ୍‌ କେତେ ଦୂରତା ଅତିକ୍ରମ କରିଥିଲା ?
• ଗାଡ଼ିଟି କେତେ ବେଗରେ ଯାଉଥିଲା ?

ଉ –
ପ୍ରାରମ୍ଭିକ ବେଗ (u) = 0, ତ୍ଵରଣ (a) = 0.1 ମି/ସେକେଣ୍ଡ², ସମୟ (t) = 2 ମିନିଟ୍ = 120 ସେକେଣ୍ଡ
ଅତିକ୍ରାନ୍ତ ଦୂରତା
ବେଗ (v) = u + at = at = 0.1 ମିଟର/ ସେକେଣ୍ଡ² × 120 ସେକେଣ୍ଡ = 12 ମିଟର/ସେକେଣ୍ଡ ।

• ଏହି ସମୟ ମଧ୍ୟରେ ବସ୍‌ 720 ମିଟର ଦୂରତା ଅତିକ୍ରମ କରିଥିଲା ।
• ଗାଡ଼ିଟି 120 ମିଟର | ସେକେଣ୍ଡ ବେଗରେ ଯାଉଥିଲା ।

14. ଗୋଟିଏ ଟ୍ରେନ୍ 90 km/h ବେଗରେ ଗତି କରୁଥିଲା । ହଠାତ୍ ଟ୍ରେନ୍‌ର ବ୍ରେକ୍ ଦେଇ ଟ୍ରେନ୍‌ଟିର ତ୍ଵରଣ 0.5 m/s² କରାଗଲା । ଟ୍ରେନ୍‌ଟି ସ୍ଥିର ହେବା ପୂର୍ବରୁ କେତେ ଦୂର ଯାଇପାରିବ ?
ଉ –
ଟ୍ରେନ୍‌ର ପ୍ରାରମ୍ଭିକ ବେଗ (u) = 90 କି.ମି./ ଘଣ୍ଟା \(\frac { 90000 }{ 3600 }\) ମିଟର / ସେକେଣ୍ଡ = 25 ମି / ସେକେଣ୍ଡ
ତ୍ଵରଣ (a) = – 0.5 ମିଟର/ ସେକେଣ୍ଡ², ଅନ୍ତିମ ବେଗ (v) = 0
v² = u² ⇒ 0 = u² + 2as

∴ ଟ୍ରେନ୍ ଟି ସ୍ଥିର ହେବା ପୂର୍ବରୁ 625 ମିଟର ଦୂରଯାଇପାରିବ ।

15. ଗୋଟିଏ କାର୍ ସ୍ଥିରାବସ୍ଥାରୁ ସମ ତ୍ଵରଣରେ ଗତି କଲା । ଏହାର ତ୍ଵରଣ 4 m/s² ହେଲେ, 3 ସେକେଣ୍ଡ ପରେ କାର୍‌ର ପରିବେଗ କେତେ ହେବ ?
ଉ –
ସ୍ଥିରାବସ୍ଥାରୁ ଗତି ଆରମ୍ଭ କରିଛି, ଅର୍ଥାତ୍ ପ୍ରାରମ୍ଭିକ ବେଗ (u) = 0, ତ୍ଵରଣ (a) = 4 ମିଟର/ ସେକେଣ୍ଡ², (t) = 3 ସେକେଣ୍ଡ
ଶେଷ ପରିବେଗ (v) = u + at = at = 4 x 3 ମିଟର / ସେକେଣ୍ଡ = 12 ମିଟର/ସେକେଣ୍ଡ ।

16. ଗୋଟିଏ ଗମ୍ବୁଜ ଉପରୁ ହାତରେ ଧରିଥିବା ପଥରଟିକୁ ଛାଡ଼ିଦେଲା ପରେ 4 ସେକେଣ୍ଡ ପରେ ତାହା ଭୂଇଁରେ ପଡ଼ିଲା । ଗମ୍ବୁଜର ଉଚ୍ଚତା କେତେ ? (g = 10 m/s²)
ଉ –
ଗମ୍ବୁଜ ଉପରୁ ପଥରଟିକୁ ଛଡ଼ାଗଲା । ତେଣୁ ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) = 0, ସମୟ (t) = 4 ସେକେଣ୍ଡ
ଗମ୍ବୁଜର ଉଚ୍ଚତା (s) = ut + \(\frac { 1 }{ 2 }\)gt² (a = g 10 ମିଟର / ସେକେଣ୍ଡ²)
= \(\frac { 1 }{ 2 }\)gt² = \(\frac { 1 }{ 2 }\) x 10 x 4 x 4 = 80 ମିଟର ।
∴ ଗମ୍ବୁଜର ଉଚ୍ଚତା ୫୦ ମିଟର ।

17. ସଳଖ ରାଜପଥରେ ସମ ତ୍ଵରଣରେ ଗତି କରୁଥିବା ଗୋଟିଏ ଗାଡ଼ିର ବେଗ 5 ସେକେଣ୍ଡରେ 10 ମି./ସେ. ରୁ 26 ମି. | ସେ. ବେଗକୁ ତ୍ୱରାନ୍ବିତ ହେଲେ, ସେହି ସମୟ ମଧ୍ୟରେ ଗାଡ଼ିଟି କେତେ ବାଟ ଗତି କରିଥବ ?
ଉ –
ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) = 10 ମିଟର/ସେକେଣ୍ଡ, ଅନ୍ତିମ ପରିବେଗ (v) = 26 ମିଟର/ସେକେଣ୍ଡ, ସମୟ (t) = 5 ସେକେଣ୍ଡ
∴ ବରଣ (a) = \(\frac { v-u }{ t }\) = \(\frac { 26-10 }{ 5 }\) = \(\frac { 16 }{ 5 }\) ମିଟର / ସେକେଣ୍ଡ²
ଅତିକ୍ରାନ୍ତ ଦୂରତା (s) = ut + \(\frac { 1 }{ 2 }\) at² = 10 x 5 + \(\frac { 1 }{ 2 }\) x \(\frac { 16 }{ 5 }\) x 5 x 5 = 50 + 40 = 90 ମିଟର |
∴ ଗାଡ଼ିଟି ୨୦ ମିଟର ଗତି କରିଥବ ।

କାର୍ଯ୍ୟାବଳୀ (Activity) :

ତୁମପାଇଁ କାମ 5.1 :
ତୁମ ଶ୍ରେଣୀ କୋଠରିର କାନ୍ଥଗୁଡ଼ିକ ସ୍ଥିର କି ଗତିଶୀଳ ?
ଉ –
ପୃଥ‌ିବୀ ଗତିଶୀଳ ହେତୁ କୋଠରିର କାନ୍ଥ ଗୁଡ଼ିକ ଗତିଶୀଳ । ବିଶ୍ଵରେ ପରମ ସ୍ଥିର କେହି ନାହାନ୍ତି । କାନ୍ଥଟି ଆପେକ୍ଷିକ ସ୍ଥିରତାରେ ଅଛି ।

ତୁମପାଇଁ କାମ 5.2
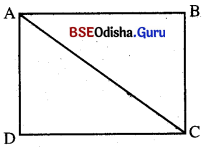
ଗୋଟିଏ ମିଟର ସ୍କେଲ୍ ଓ ଏକ ଲମ୍ବା ରସି ସଂଗ୍ରହ କର । ତୁମ ବିଦ୍ୟାଳୟର ଆୟତାକାର ଫୁଟ୍‌ବଲ୍‌ ପଡ଼ିଆ ବା ଭଲିବଲ୍ କୋର୍ଟର ଗୋଟିଏ କୋଣରେ ତୁମେ ତୁମ ସାଙ୍ଗ ସହିତ ଠିଆ ହୁଅ । ତୁମ ସାଙ୍ଗକୁ ପଡ଼ିଆ ବା କୋର୍ଟର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଦେଇ ତୁମର ବିପରୀତ କୋଣକୁ ଯିବାକୁ କୁହ । ଏହି ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥକୁ ମାପିରଖ । ତୁମ ସାଙ୍ଗ ଅତିକ୍ରାନ୍ତ କରୁଥିବା ଦୂରତା ଓ ବିସ୍ଥାପନର ପରିମାଣ କେତେ ? ଉଭୟ ପରିମାଣ ମଧ୍ଯରେ କିଛି ପ୍ରଭେଦ ଦେଖୁଛି କି ? (ମନେକର ଦୈର୍ଘ୍ୟ = x ମିଟର ଓ ପ୍ରସ୍ଥ = y ମିଟର ।)
ଉ –
ABCD ଆୟତାକାର ପଡ଼ିଆର ଦୈର୍ଘ୍ୟ = AB = x ମି.
ଓ ପ୍ରସ୍ଥ = BC = y ମି.
ତୁମେ ଓ ତୁମ ସାଙ୍ଗ ଠିଆ ହୋଇଥିବା ସ୍ଥାନ ବା ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁ = A
ତୁମ ସାଙ୍ଗ ପହଞ୍ଚିବା ସ୍ଥାନ ବା ଅନ୍ତିମ ବିନ୍ଦୁ = C
ତୁମ ସାଙ୍ଗର ଅତିକ୍ରାନ୍ତ ଦୂରତା = AB + BC = (x + y)
ମିଟର ବିସ୍ଥାପନ = AC = \(\sqrt{x^2+y^2}\) ମିଟର ।

ତୁମପାଇଁ କାମ 5.3 :
ଗୋଟିଏ ମଟରଗାଡ଼ି ଭୁବନେଶ୍ଵରରୁ ବାହାରି ନୂଆଦିଲ୍ଲୀ ଗଲା । ତାହାର ପ୍ରାରମ୍ଭିକ ଓ ଅନ୍ତିମ ପାଠ୍ୟଙ୍କ (readings) ମଧ୍ୟରେ ପ୍ରଭେଦ 1850 କି.ମି. ଅଟେ । ଭୁବନେଶ୍ୱରରୁ ନୂଆଦିଲ୍ଲୀର ଦୂରତା କେତେ ? ଭୁବନେଶ୍ଵର ଓ ନୂଆଦିଲ୍ଲୀ ମଧ୍ଯରେ ମଟରଗାଡ଼ିର ବିସ୍ଥାପନ କେତେ ?
ଉ –
ଭୁବନେଶ୍ୱରରୁ ନୂଆଦିଲ୍ଲୀର ଦୂରତା 1850 କି.ମି. ଅଟେ । ଭୁବନେଶ୍ଵର ଓ ନୂଆଦିଲ୍ଲୀ ମଧ୍ୟରେ ମଟରଗାଡ଼ିର ବିସ୍ଥାପନ 1850 କି.ମି. ଅଟେ ।

ତୁମପାଇଁ କାମ 5.4 :
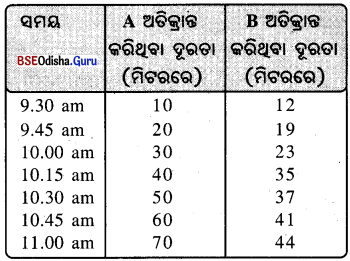
ଦୁଇଟି ବସ୍ତୁ A ଓ Bର ଗତିକୁ ସାରଣୀରେ ଦର୍ଶାଯାଇଛି । ପାର୍ଶ୍ୱସ୍ଥ ସାରଣୀକୁ ନିରୀକ୍ଷଣ କରି ସେମାନଙ୍କର ଗତି ସମଗତି ବା ଅସମଗତି ଭାବି କୁହ ।
ଭ –
ସାରଣୀରୁ ଜଣାଯାଇଛି, ବସ୍ତୁ Aର ଗତି ସମଗତି ଓ ବସ୍ତୁ Bର ଗତି ଅସମଗତି । କାରଣ ବସ୍ତୁ A ସମାନ ସମୟ ଅନ୍ତରାଳରେ ସମାନ ପଥ ଅତିକ୍ରମ କରୁଛି କିନ୍ତୁ ବସ୍ତୁ B ସମାନ ସମୟ ଅନ୍ତରାଳରେ ଅସମାନ ପଥ ଅତିକ୍ରମ କରୁଛି ।

ତୁମପାଇଁ କାମ 5.5 :
ତୁମକୁ ଘରୁ ଚାଲି ଚାଲି ବିଦ୍ୟାଳୟକୁ ଯିବାକୁ ଯେତିକି ସମୟ ଲାଗେ ତାହାକୁ ଖାତାରେ ଟିପିରଖ । ଯଦି ରୁମର ତ୍ବାରାହାରି ଦେଖ \(\frac { 4km }{ h }\) ହୁଏ, ତାହାହେଲେ ତୁମ ଘରଠାରୁ ବିଦ୍ୟାଳୟର ଦୂରତା କେତେ ?
ଭ –
ମୋତେ ଘରୁ ଚାଲି ଚାଲି ବିଦ୍ୟାଳୟରେ ପହଞ୍ଚିବା ପାଇଁ 15 ମିନିଟ୍ ସମୟ ଲାଗେ ।
ଅର୍ଥାତ୍ ସମୟ (t) = 15 ମିନିଟ୍ = \(\frac { 1 }{ 4 }\) h, ହାରାହାରି ବେଗ (v) = 4 \(\frac { km }{ h }\)
∴ ଘରଠାରୁ ବିଦ୍ୟାଳୟର ଦୂରତା (s) = vt = 4\(\frac { km }{ h }\) x \(\frac { 1 }{ 4 }\) h = 1km

ତୁମପାଇଁ କାମ 5.6 :
ବର୍ଷାବେଳେ ତୁମେ ବିଜୁଳି ଦେଖୁବାର କିଛି ସମୟ ପରେ ଘଡ଼ଘଡ଼ିର ଧ୍ୱନି ଶୁଣ । ଏପରି କାହିଁକି ହୁଏ ? ଆଲୋକ ଓ ଧ୍ଵନିର ବେଗଦ୍ଵାରା ଏହାକୁ ବୁଝାଅ ।
ଭ –
ବିଜୁଳି ଓ ଘଡ଼ଘଡ଼ି ଏକା ସମୟରେ ସୃଷ୍ଟି ହୁଏ । ଧ୍ଵନିର ବେଗ 330 m/s ବେଳେ ଆଲୋକର ବେଗ 3 × 10⁸ m/s ଅଟେ । ତେଣୁ ବିଜୁଳିକୁ ଆମେ ପ୍ରଥମେ ଦେଖୁ ଓ ପରେ ଘଡ଼ଘଡ଼ି ଶବ୍ଦ ଶୁଣିବାକୁ ମିଳେ ।

ତୁମପାଇଁ କାମ 5.7 :
ତୁମେ ଦୈନନ୍ଦିନ ଜୀବନରେ ବିଭିନ୍ନ ପ୍ରକାର ଗତିର ସମ୍ପର୍କରେ ଆସୁଛ । ଦିଆଯାଇଥିବା ତଥ୍ୟକୁ ଭିଭିକରି ପ୍ରତ୍ୟେକ ପ୍ରକାର ଗତିର ଗୋଟିଏ ଲେଖାଏଁ ଉଦାହରଣ ଦିଅ । ଯେଉଁଠି :
(a) ତ୍ଵରଣ, ଗତିର ବିପରୀତ ଦିଗରେ ଥାଏ ।
(b) ତ୍ଵରଣ, ଗତି ଦିଗର ବିରୁଦ୍ଧାଚରଣ କରେ ।
(c) ଗତିର ସମ ତ୍ଵରଣ ଥାଏ ।
(d) ଗତିର ଅସମ ତ୍ଵରଣ ଥାଏ ।
ଉ –
(a) ଉପରକୁ ସିଧାଭାବରେ ଫିଙ୍ଗିଥିବା ଏକ ବଲ୍‌ର ଗତି ।
(b) ସ୍ରୋତର ପ୍ରତିକୂଳରେ ଗତି କରୁଥିବା ଏକ ଡଙ୍ଗାର ଗତି ।
(c) ଗଛରୁ ପଡ଼ୁଥିବା ଏକ ଫଳର ଗତି ।
(d) ଜନଗହଳି ରାସ୍ତାରେ ଗତି କରୁଥିବା କାର୍‌ର ଗତି ।

ତୁମପାଇଁ କାମ 5.8 :
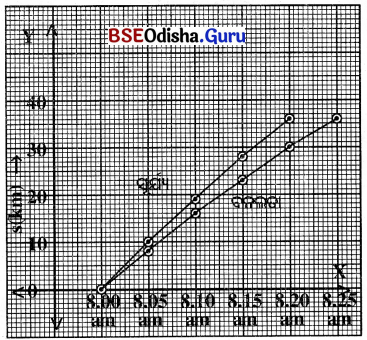
ସମବେଗରେ ଗତି କରୁଥିବା ଗୋଟିଏ ଟ୍ରେନ୍ ର ତିନୋଟି ଷ୍ଟେସନ; ଯଥା- A, B ଓ Cରେ ପହଞ୍ଚିବାର ଏବଂ ଛାଡ଼ିବାର ସମୟ ଏବଂ A ଷ୍ଟେସନଠାରୁ B ଓ Cର ଦୂରତାକୁ ସାରଣୀରେ ଦିଆଯାଇଛି । ଏହି ତଥ୍ୟକୁ ନେଇ ଏକ ସମୟ –ଦୂରତା ଗ୍ରାଫ୍ ଅଙ୍କନ କର ।

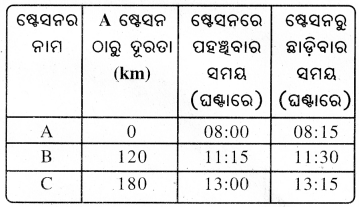
ଉ –

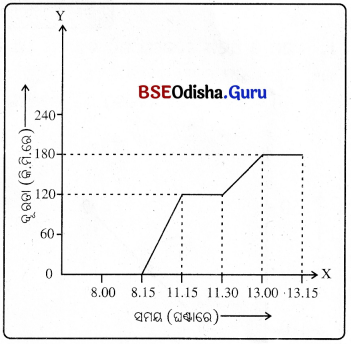
ତୁମପାଇଁ କାମ 5.9 :
ସୂର୍ଯ୍ୟ ଓ ତାହାର ଭଉଣୀ ବନଲତା ତାଙ୍କ ଘରଠାରୁ 3.6 km ଦୂରରେ ଥ‌ିବା ବିଦ୍ୟାଳୟକୁ ସାଇକେଲରେ . ଯାଆନ୍ତି । ସେମାନେ ଘରୁ ଏକା ସମୟରେ ବାହାରି ସମାନ ବାଟ ଦେଇ ବିଦ୍ୟାଳୟକୁ ଯାଉଥିଲେ ମଧ୍ୟ ଅଲଗା ଅଲଗା ସମୟରେ ବିଦ୍ୟାଳୟରେ ପହଞ୍ଚି’ନ୍ତି । ସାରଣ1ରେ ସେମାନଙ୍କର ବିଭନ୍ନ ସମୟରେ ଅତିକ୍ରାନ୍ତ ଦୂରତାକୁ ଦିଆଯାଇଛି । ଏହାକୁ ଦୁଇଟି ଅଲଗା ଅଲଗା ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଅଙ୍କନ କର ଓ ବ୍ୟାଖ୍ୟା କର ।

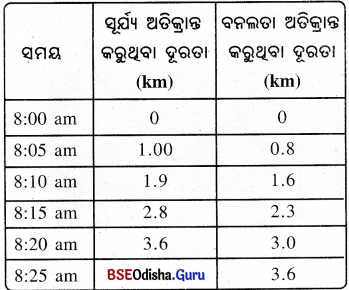
ଏହି ଗ୍ରାଫ୍‌ ଜଣାଯାଏ ଯେ ସମାନ ଦୂରତା ଅତିକ୍ରମ ପାଇଁ ସୂର୍ଯ୍ୟ ଅପେକ୍ଷା ବନଲତା ଅଧ‌ିକ ସମୟ ନେଇଛି ।
ଉ –