Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(j) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(j)
Question 1.
Δ ABC ଅଙ୍କନ କର ଯାହାର AB = 8 ସେ.ମି., AC = 4 ସେ.ମି. ଓ BC = 6 ସେ.ମି. । ଉପରେ ତ୍ରିଭୁଜର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ଆୟତକ୍ଷେତ୍ର ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
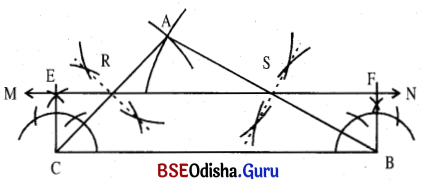
(a) AB = 8 ସେ.ମି., AC = 4 ସେ.ମି. ଓ BC = 6 ସେ.ମି. ନେଇ Δ ABC ଅଙ୍କନ କର ।
(b) AC ଓ AB ର ମଧ୍ୟବିନ୍ଦୁ ଯଥାକ୍ରମେ R ଓ S ନିର୍ଣ୍ଣୟ କରି, ଉକ୍ତ ବିନ୍ଦୁମାନଙ୍କ ମଧ୍ୟଦେଇ \(\overleftrightarrow{\mathrm{MN}}\) ଅଙ୍କନ କର ।
(c) C ବିନ୍ଦୁରେ ଅଙ୍କିତ ଲମ୍ବ C͞E ଅଙ୍କନ କର ।
(d) \(\overleftrightarrow{\mathrm{MN}}\) ଉପରେ F ଏପରି ଏକ ବିନ୍ଦୁ ନିଅ, ଯେପରିକି CB = EF ହେବ ।
(e) BF ଅଙ୍କନ କରି ECBF ଆୟତକ୍ଷେତ୍ର ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 2.
Δ ABC ର AB = 5 ସେ.ମି., AC = 4 ସେ.ମି., m∠A = 60°, ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରି BC ଉପରେ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ଆୟତକ୍ଷେତ୍ର ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
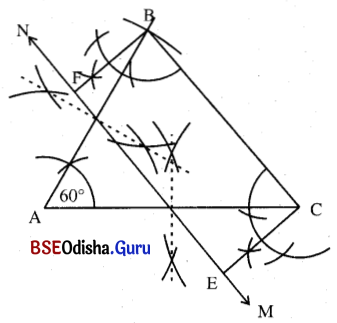
(a) AB = 5 ସେ.ମି., AC = 4 ସେ.ମି. ଓ m∠A = 60° ନେଇ Δ ABC ଅଙ୍କନ କର ।
(b) A͞C ଓ A͞B ର ମଧ୍ୟବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କରି ଉକ୍ତ ବିନ୍ଦୁମାନଙ୍କ ମଧ୍ୟଦେଇ MN ଅଙ୍କନ କର ।
(c) C ଓ ବିନ୍ଦୁରେ C͞E ଲମ୍ବ ଅଙ୍କନ କର ।
(d) \(\overleftrightarrow{\mathrm{MN}}\) ଉପରେ F ଏପରି ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି CB = EF ହେବ ।
(e) B͞F ଅଙ୍କନ କରି ଆବଶ୍ୟକୀୟ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଆୟତକ୍ଷେତ୍ର ସମ୍ପୂର୍ଣ୍ଣ ECBF ଆୟତକ୍ଷେତ୍ର ସମ୍ପୂଣ୍ଡି କର ।
![]()
Question 3.
Δ ABC ଅଙ୍କନ କର ଯାହାର a + b + c = 8.5 ସେ.ମି. m∠B = 60° ଏବଂ m∠C = 90° । ଏହାର ଦୁଇଗୁଣ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଆୟତକ୍ଷେତ୍ର ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
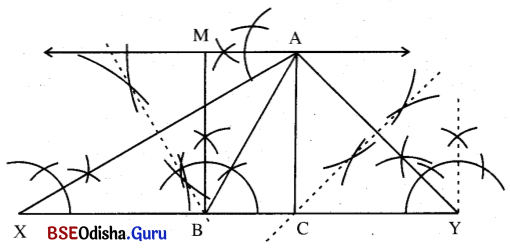
(a) 8.5 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ X͞Y ଅଙ୍କନ କର ।
(b) X ଓ Y ବିନ୍ଦୁରେ 30° ଏବଂ 45 ପରିମାଣ ବିଶିଷ୍ଟ ଯଥାକ୍ରମେ ∠AXY ଏବଂ ∠AYX ଅଙ୍କନ କର ।
(c) AX ଓ AY ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ XY କୁ ଯଥାକ୍ରମେ B ଓ C ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତୁ ।
(d) AB ଓ AC ଅଙ୍କନ କରି Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(e) A ବିନ୍ଦୁରେ B͞C ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{AM}}\) ଅଙ୍କନ କର ।
(f) B ବିନ୍ଦୁରେ ଅଙ୍କିତ ଲମ୍ବ \(\overleftrightarrow{\mathrm{AM}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(g) MBCA ଆବଶ୍ୟକୀୟ Δ ABC ର ଦୁଇଗୁଣ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଆୟତଚିତ୍ର ।
Question 4.
Δ ABC ଅଙ୍କନ କର ଯାହାର AB – AC = 1.5 ସେ.ମି., BC = 6.3 ସେ.ମି., m∠B = 45° । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ଆୟତକ୍ଷେତ୍ର ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
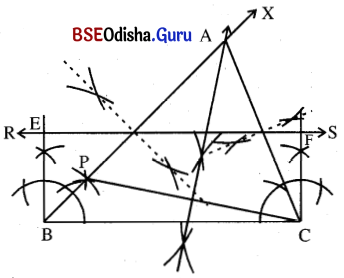
(a) 6.3 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ BC ଅଙ୍କନ କର ।
(b) B ବିନ୍ଦୁରେ ∠XBC ଅଙ୍କନ କର ଯାହାର ପରିମାଣ 45° ହେବ ।
BX ଉପରେ P ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି BP = 1.5 ସେ.ମି. ।
(c) PC ଅଙ୍କନ କର । PC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ \(\overrightarrow{\mathrm{BX}}\) କୁ A ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(d) AC ଅଙ୍କନ କରି Δ ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
(e) AB ଓ AC ର ମଧ୍ୟବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କରି ଉକ୍ତ ବିଦୁଦେଇ \(\overleftrightarrow{\mathrm{RS}}\) ଅଙ୍କନ କର ।
(f) B ବିନ୍ଦୁରେ ଅଙ୍କିତ ଲମ୍ବ B͞E ଅଙ୍କନ କର, ଯାହା \(\overleftrightarrow{\mathrm{RS}}\) କୁ E ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
\(\overleftrightarrow{\mathrm{RS}}\) ଉପରେ F ଚିହ୍ନଟ କର ଯେପରି BC = EF ହେବ କିମ୍ବା CF ⊥ BC ।
(g) BCFE ଆବଶ୍ୟକୀୟ ଆୟତକ୍ଷେତ୍ର ।
