BSE Odisha 9th Class Maths Notes Geometry Chapter 7 ତ୍ରିକୋଣମିତି

Odisha State Board BSE Odisha 9th Class Maths Notes Geometry Chapter 7 ତ୍ରିକୋଣମିତି will enable students to study smartly.

BSE Odisha Class 9 Maths Notes Geometry Chapter 7 ତ୍ରିକୋଣମିତି

ଉପକ୍ରମ (Introduction):

• ତ୍ରିକୋଣମିତି (Trigonometry) ଶବ୍ଦର ଅର୍ଥ ତିନି କୋଣର ପରିମାପ ।
• ଗ୍ରୀକ୍ ଜ୍ୟୋତିର୍ବିଦ୍ Hipparchus(140 B.C.) ତ୍ରିକୋଣମିତିର ଆବିଷ୍କାର କରିଥିଲେ ।
• ଗଣିତଜ୍ଞ Bertholomaus Pitisces ଷୋଡ଼ଶ ଶତାବ୍ଦୀରେ ପ୍ରଥମ ତ୍ରିକୋଣମିତି ଗ୍ରନ୍ଥ ରଚନା କରିଥିଲେ । 

ତ୍ରିକୋଣମିତିକ ଅନୁପାତ (Trigonometrical Ratios) :
(i) ABC ସମକୋଣୀ ତ୍ରିଭୁଜରେ m/ABC = 90° । ମନେକର m∠BCA = θ° (0 = ଥଟା) । A͞C କୁ କଣ୍ଠ (hypotenuse), ∠BCAର ସଂଲଗ୍ନ ବାହୁ BC କୁ ଭୂମି (base) ଓ ∠BCAର ସମ୍ମୁଖୀନ ବାହୁ AB କୁ ଲମ୍ବ (perpendicular) କୁହାଯାଏ । ସଂକ୍ଷେପରେ BC = b, AB = p ଓ AC = h ଲେଖାଯାଏ ।

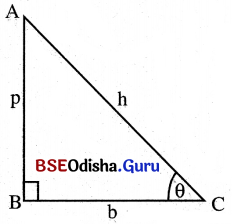
(ii) p, b ଓ hରୁ ଯେକୌଣସି ଦୁଇଗୋଟିର୍ ଅନୁପାତ, 8 କୋଣର ଏକ ତ୍ରିକୋଣମିତିକ ଅନୁପାତ । ସମୁଦାୟ ଛଅଗୋଟି ତ୍ରିକୋଣମିତିକ ଅନୁପାତ; ଯଥା – sine, cosine, tangent, cotangent, secant ଓ cosecant ଅଛନ୍ତି । ସଂକ୍ଷିପ୍ତଭାବେ ଏଗୁଡ଼ିକ sin (ସାଇନ୍), cos (କସ୍), tan(ଟାନ୍), cot (କଟ୍), sec (ସେକ୍) ଓ cosec (କ୍ରୋସେକ୍) ବୋଲି ଲେଖାଯାଏ ।

ତ୍ରିକୋଣମିତିକ ଅନୁପାତଗୁଡ଼ିକ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ (Relations among trigonometrical Ratios) : 

(a) ବ୍ୟତ୍‌କ୍ରମ ସମ୍ପର୍କ (Reciprocal Relation) :

• sin θ × cosec θ = 1, sin θ = \(\frac{1}{{cosec} \theta}\) cosec θ = \(\frac{1}{{sin} \theta}\)
• cos θ × sec θ = 1, cos θ = \(\frac{1}{{sec} \theta}\) sec θ = \(\frac{1}{{cos} \theta}\)
• tan θ × cot θ = 1, tan θ = \(\frac{1}{{cot} \theta}\) cot θ = \(\frac{1}{{tan} \theta}\)

ବର୍ଗ ସମ୍ପର୍କ (Square Relation):

(i) sin² θ + cos² θ = 1, sin² θ = 1 – cos² θ, cos² θ = 1 – sin² θ
(ii) cosec² θ – cot² θ = 1, cosec² θ = 1 + cot² θ, cot² θ = cosec² θ – 1
(iii) sec² θ – tan² θ = 1, sec² θ = 1 + tan² θ, tan² θ = sec² θ – 1

ଭାଗକ୍ରିୟା ସମ୍ପର୍କ (Quotient Relation):
tan θ = \(\frac{\sin \theta}{\cos \theta}\) ଏବଂ cot θ = \(\frac{\cos \theta}{\sin \theta}\)

ସରଳ ତ୍ରିକୋଣମିତିକ ଅଭେଦ (Simple Trigonometrical Indentities) :
(i) ପ୍ରତ୍ୟେକ ସୂତ୍ର ଗୋଟିଏ ଗୋଟିଏ ଅଭେଦ । ଅଭେଦରେ θ (ଥ୍ଟା) ପରିବର୍ତ୍ତେ α (ଆଲ୍‌ଫା), β (ବିଟା) ଏବଂ γ (ଗାମା) ଆଦି ଗ୍ରୀକ୍ ଅକ୍ଷର ମଧ୍ୟ ବ୍ୟବହୃତ ହୁଏ ।
(ii) ଅଭେଦଗୁଡ଼ିକର ଦୁଇଟି ପାର୍ଶ୍ଵ ଯଥା : ବାମପାର୍ଶ୍ବ ଓ ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ ଥାଏ ।
(iii) ଅଭେଦଗୁଡ଼ିକର ପ୍ରମାଣ ପାଇଁ ସାଧାରଣତଃ ଯେକୌଣସି ପାର୍ଶ୍ୱରୁ ଆରମ୍ଭ କରି ଅନ୍ୟ ପାର୍ଶ୍ଵରେ ପହଞ୍ଚିବାକୁ ପଡ଼େ; ଯାହାଦ୍ୱାରା ଅଭେଦଗୁଡ଼ିକର ପ୍ରମାଣ ସମ୍ଭବ ହୋଇଥାଏ ।
(iv) ଉଭୟ ପାର୍ଶ୍ଵକୁ ଏକ ସାଧାରଣ ସୋପାନରେ ପହଞ୍ଚାଇ ଅଭେଦଗୁଡ଼ିକର ପ୍ରମାଣ କରାଯାଇପାରେ ।
(vi) ଅଭେଦଗୁଡ଼ିକର ପ୍ରମାଣ ପାଇଁ ବୀଜଗାଣିତିକ ସୂତ୍ର ବା ଅଭେଦର ସାହାଯ୍ୟ ନିଆଯାଇଥାଏ ।
(vii) ଏଠାରେ ମନେରଖୁବାକୁ ହେବ ଯେ, θ ବା α ବା βର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନ ପାଇଁ ଅଭେଦର ଉଭୟ ପାର୍ଶ୍ଵ ସମାନ ହୋଇଥାଏ ।

କେତେଗୋଟି ନିର୍ଦ୍ଦିଷ୍ଟ କୋଣର ତ୍ରିକୋଣମିତିକ ଅନୁପାତ (Trigonometrical Ratios of some particular angles) :
θର ମାନ 30°, 45° ଓ 60° ନେଇ ତ୍ରିକୋଣମିତିକ ଅନୁପାତ sin θ, cos θ, tan θ, cosec θ, sec θ ଓ tan θ ଇତ୍ୟାଦିର ମୂଲ୍ୟ ନିରୂପିତ କରାଯାଇଥାଏ ।

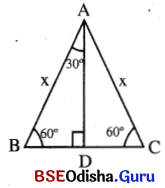
θ = 30° ଓ 60° ନେଇ ତ୍ରିକୋଣମିତିକ ଅନୁପାତ ନିର୍ଣ୍ଣୟ ମନେକର ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ଓ
ଏହାର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = x ଏକକ ।
∴ Δ ABC ର AB = BC = CA = x ଏକକ
ଓ m∠A = m∠B = m∠C = 60° 
A ବିନ୍ଦୁରୁ ବିପରୀତ ବାହୁ BC ପ୍ରତି AD ଲମ୍ବ ଅଙ୍କନ କରାଯାଉ ।
BC = x ଏକକ ∴ BD = \(\frac{1}{2}\) BC = \(\frac{1}{2}\) . x = \(\frac{x}{2}\) ଏକକ

θ = 45° ନେଇ ତ୍ରିକୋଣମିତିକ ଅନୁପାତ ନିଶ୍ଚୟ
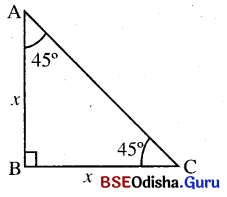
ମନେକର ABC ଏକ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ । ଏହାର AB = BC = x ଏକକ
ଓ m∠A = m∠C = 45° ହେଲେ,
AC = \(\sqrt{A B^2+B C^2}\) = \(\sqrt{x^2+x^2}\) = \(\sqrt{2x^2}\) = √2x ଏକକ
∠C ର ତ୍ରିକୋଣମିତିକ ଅନୁପାତଗୁଡ଼ିକ ନେଲେ



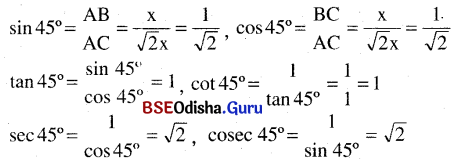
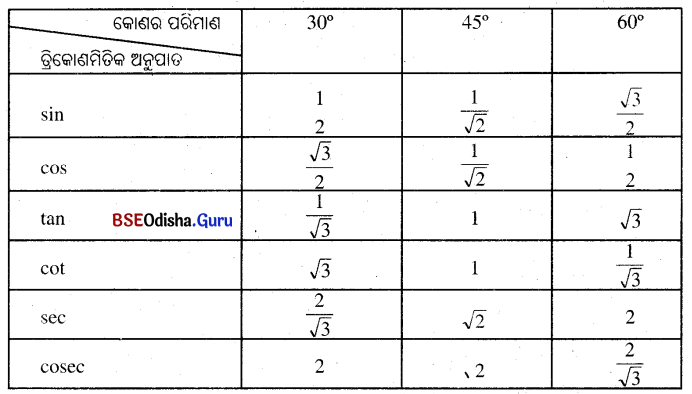
ଏଠାରେ sin 30° = cos 60°, tan 30° = cot 60°, sec 30° = cosec 60°. sin 60° = cos 30°, tan 60° = cot 30°, sec 60° = cosec 30°, sin 45° = cos 45°, tan 45° = cot 45° ଏବଂ sec 45° = cosec 45°