Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 7 ତ୍ରିଭୁଜର ଧର୍ମ InText Questions Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 7 ତ୍ରିଭୁଜର ଧର୍ମ InText Questions
(କ) ସେହିଭଳି ∠B ଓ ∠C ର ସମ୍ମୁଖୀନ ବାହୁ ସ୍ଥିର କର ।
ସମାଧାନ:
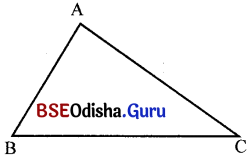
Δ ABC ରେ ∠B ର ସମ୍ମୁଖୀନ ବାହୁ AC ଏବଂ ∠C ର ସମ୍ମୁଖୀନ ବାହୁ AB ।
(ଖ) XYZ ନାମକ ଗୋଟିଏ ତ୍ରିଭୁଜ ଅଙ୍କନ କର । ଏହାର X͞Y, Y͞Z ଓ Z͞X ର ସମ୍ମୁଖୀନ କୋଣଗୁଡ଼ିକର ନାମ ଲେଖ ।
ସମାଧାନ:
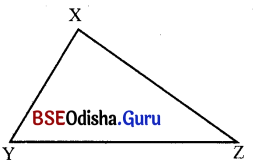
XY ର ସମ୍ମୁଖୀନ ବାହୁ ∠Z
YZ ର ସମ୍ମୁଖୀନ ବାହୁ ∠X ଓ
ZX ର ସମ୍ମୁଖୀନ ବାହୁ ∠Y ।
ଉତ୍ତର ଲେଖ :
1. Δ ABC ର ପ୍ରତ୍ୟେକ ଶୀର୍ଷ ବିନ୍ଦୁରେ କେତୋଟି ବହିଃସ୍ଥ କୌଣ ଅଙ୍କନ ସମ୍ଭବ ?
ସମାଧାନ:
ଦୁଇଟି ।
2. Δ ABC ର A ଶୀର୍ଷ ବିନ୍ଦୁଠାରେ ବହିଃସ୍ଥ କୋଣ ଦୁଇଟି ଅଙ୍କନ କଲେ, ସେ ଦୁଇଟିର ପରିମାଣ ମଧ୍ୟରେ କି ସମ୍ପର୍କ ରହିବ ? ତୁମ ଉତ୍ତରର କାରଣ କ’ଣ ?
ସମାଧାନ:
ସେ ଦୁଇଟିର ପରିମାଣ ସମାନ, କାରଣ ପ୍ରତ୍ୟେକ ବହିଃସ୍ଥ କୋଣ ∠A ର ସନ୍ନିହିତ ପରିପୂରକ କୋଣ ।
3. ଏକ ତ୍ରିଭୁଜର ଗୋଟିଏ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ଓ ତା’ର ସନ୍ନିହିତ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ ମଧ୍ୟରେ ସମ୍ପର୍କ କ’ଣ ? ତୁମ ଉତ୍ତରର କାରଣ କହି ।
ସମାଧାନ:
ତ୍ରିଭୁଜର ବହିଃସ୍ଥ ଏବଂ ଏହାର ସନ୍ନିହିତ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣର ସମଷ୍ଟି 180°; କାରଣ ସେ କୋଣଦ୍ଵୟ ପରସ୍ପର ପରିପୂରକ ।
![]()
ନିଜେ କରି ଦେଖ :
1. ତୁମ ଖାତାରେ ତିନୋଟି ବିଭିନ୍ନ ଆକୃତିର ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
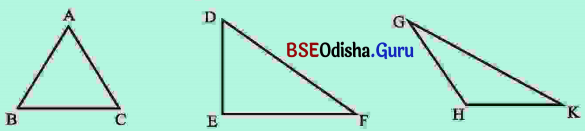
2. ପ୍ରୋଟ୍ରାକ୍ଟର ବ୍ୟବହାର କରି ତ୍ରିଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ଓ ସେଗୁଡ଼ିକୁ ନିମ୍ନ ସାରଣୀରେ ଯଥା ସ୍ଥାନରେ ଲେଖ । (ପ୍ରଶ୍ନ ସହ ଉତ୍ତର)
| ତ୍ରିଭୁଜର ନାମ | କୋଣ ତିନୋଟିର ପରିମାଣ | କୋଣ ତିନୋଟିର ପରିମାଣର ସମଷ୍ଟି |
| Δ ABC | m∠A = m∠B = m∠C = |
_________ + _________ + _________ = _________ |
| Δ DEF | m∠D = m∠E = m∠F = |
_________ + _________ + _________ = _________ |
| Δ GHK | m∠G = m∠H = m∠K = |
_________ + _________ + _________ = _________ |
ସମାଧାନ:
| ତ୍ରିଭୁଜର ନାମ | କୋଣ ତିନୋଟିର ପରିମାଣ | କୋଣ ତିନୋଟିର ପରିମାଣର ସମଷ୍ଟି |
| Δ ABC | m∠A = 80° m∠B = 45° m∠C = 55° |
80° + 45° + 55° = 180° |
| Δ DEF | m∠D = 50° m∠E = 90° m∠F = 40° |
50° + 90° + 40° = 180° |
| Δ GHK | m∠G = 19° m∠H = 140° m∠K = 21° |
19° + 140° + 21° = 180° |
3. ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ କୋଣ ତିନୋଟିର ପରିମାଣର ସମଷ୍ଟି କେତେ ହେବାର ଦେଖୁଛ ?
ସମାଧାନ:
180°
ତୁମେ ଉତ୍ତର ନିର୍ଣ୍ଣୟ କରିବାକୁ ଚେଷ୍ଟା କର :
1. Δ ABC ର m∠A= 70° ଓ m∠B = 45° ହେଲେ m∠C କେତେ ?
ସମାଧାନ :
Δ ABC ର m∠A = 70° ଓ m∠B = 45° । ମନେକର m∠C = x°
ଆମେ ଜାଣୁ m∠A + m∠B + m∠C = 180°
⇒ 70° + 45° + x = 180°
⇒ x = 180° – 115° = 65°
∴ ∠C ର ପରିମାଣ 65° ।
2. Δ POR ରେ m∠R ଅପେକ୍ଷା m∠Q 10° ଅଧୁକ ଓ m∠Q ଠାରୁ m∠P 10° ଅଧିକ ହେଲେ, କୋଣ ତିନୋଟିର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର Δ POR ରେ m∠R = x° କିନ୍ତୁ m∠Q = m∠R + 10° = (x + 10)°
m∠P = m∠Q + 10°
= (x + 10 + 10)°
= (x + 20°)
Δ PQR ରେ m∠P + m∠Q + m∠R = 180°
⇒ x + 20 + x + 10 + x = 180°
⇒ 3x + 30 = 180°
⇒ 3x = 180° – 30° = 150°
⇒ x = \(\frac{150°}{3}\) = 50°
∴ m∠P = (x + 20)° = (50 + 20)° = 70°,
m∠Q = (x + 10)° = (50 + 10)° = 60° ଏବଂ m∠R = x° = 50° ।
![]()
ନିଜେ କରି ଦେଖ :
1. ତୁମ ଖାତାରେ ତିନୋଟି ଭିନ୍ନ ଭିନ୍ନ ତ୍ରିଭୁଜ ଅଙ୍କନ କର । ସେ ତ୍ରିଭୁଜ ତିନୋଟିର ନାମ ଦିଅ ABC, PQR, XYZ ।
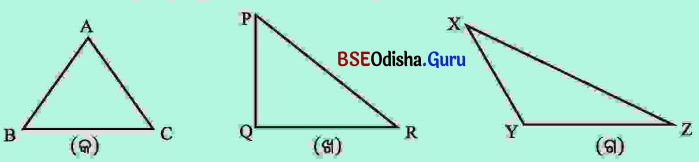
2. ପ୍ରତ୍ୟେକ ତ୍ରିଭୁଜର ବାହୁଗୁଡ଼ିକର ଦୈର୍ଘ୍ୟ ମାପ ଓ ନିମ୍ନ ସାରଣୀ ପୂରଣ କର (ଶେଷ ସ୍ତମ୍ଭରେ (3) ଓ ସ୍ତମ୍ଭ (4) ର ଫଳ ମଧ୍ୟରୁ କେଉଁଟି ବୃହତ୍ତର ଲେଖ ।)
| ତ୍ରିଭୁଜର ନାମ (1) |
ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ (2) |
ଦୁଇଟି ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି (3) |
ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ (4) |
ସ୍ତମ୍ଭ (3) ଓ (4) ଫଳାଫଳ ମଧ୍ୟରେ ତୁଳନା (5) |
| Δ ABC | AB = BC = CA = |
AB + BC = | AC = | |
| AB + AC = | BC = | |||
| BC + AC = | AB = | |||
| Δ PQR | PQ = | PQ + QR = | RP = | |
| QR = | QR + RP = | PQ = | ||
| RP = | PQ + RP = | QR = | ||
| Δ XYZ | XY = | XY + YZ = | ZX = | |
| YZ = | YZ + ZX = | XY = | ||
| ZX = | XY + ZX = | YZ = |
ସମାଧାନ:
| ତ୍ରିଭୁଜର ନାମ (1) |
ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ (2) |
ଦୁଇଟି ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି (3) |
ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ (4) |
ସ୍ତମ୍ଭ (3) ଓ (4) ଫଳାଫଳ ମଧ୍ୟରେ ତୁଳନା (5) |
| Δ ABC | AB = 3.4 ସେ.ମି. BC = 5 ସେ.ମି. CA = 4.2 ସେ.ମି. |
AB + BC = 8.4 ସେ.ମି. | AC = 4.2 ସେ.ମି. | AB + BC > AC |
| AB + AC = 7.6 ସେ.ମି. | BC = 5 ସେ.ମି. | AB + AC > BC | ||
| BC + AC = 9.2 ସେ.ମି. | AB = 3.4 ସେ.ମି. | AC + BC > AB | ||
| Δ PQR | PQ = 3 ସେ.ମି. QR = 4 ସେ.ମି. RP = 5 ସେ.ମି. |
PQ + QR = 7 ସେ.ମି. | RP = 5 ସେ.ମି. | PQ + QR > RP |
| QR + RP = 9 ସେ.ମି. | PQ = 3 ସେ.ମି. | QR + RP > PQ | ||
| PQ + RP = 8 ସେ.ମି. | QR = 4 ସେ.ମି. | PQ + RP > QR | ||
| Δ XYZ | XY = 4 ସେ.ମି. YZ = 2.5 ସେ.ମି. ZX = 6 ସେ.ମି. |
XY + YZ = 6.5 ସେ.ମି. | ZX = 6 ସେ.ମି. | XY + YZ > ZX |
| YZ + ZX = 8.5 ସେ.ମି. | XY = 4 ସେ.ମି. | YZ + ZX > XY | ||
| XY + ZX = 10 ସେ.ମି. | YZ = 2.5 ସେ.ମି. | XY + ZX > YZ |
3. ଉପରିସ୍ଥ ସାରଣୀର ସ୍ତମ୍ଭ (5) ରୁ ଆମେ କ’ଣ ଜାଣିଲେ ?
ସମାଧାନ:
ଗୋଟିଏ ତ୍ରିଭୁଜର ଯେକୌଣସି ଦୁଇଟି ବାହୁର ଦୈର୍ଘ୍ୟ ସମଷ୍ଟି ଏହାର ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ବୃହତ୍ତର ।
![]()
4. Δ POR ର PQ = 8 ସେ.ମି. ଓ PR = 11 ସେ.ମି., ନିମ୍ନ ଉକ୍ତିମାନଙ୍କ ମଧ୍ୟରୁ ଠିକ୍ ଭକ୍ତିକୁ ବାଛ ।
(କ) QR, 2 ସେ.ମି. ଠାରୁ ଅଧୁକ ଓ 19 ସେ.ମି. ଠାରୁ କମ୍
(ଖ) QR, 3 ସେ.ମି. ଠାରୁ ଅଧୁକ ଓ 20 ସେ.ମି. ଠାରୁ କମ୍
(ଗ) QR, 3 ସେ.ମି. ଠାରୁ ଅଧୁକ ଓ 19 ସେ.ମି ଠାରୁ କମ୍
(ଘ) QR, 2 ସେ.ମି. ଠାରୁ ଅଧୁକ ଓ 20 ସେ.ମି. ଠାରୁ କମ୍ ତୁମର ଉତ୍ତର ସପକ୍ଷରେ କାରଣ ଦର୍ଶାଅ ।
ସମାଧାନ:
PQ + PR = 8 ସେ.ମି. + 11 ସେ.ମି. = 19 ସେ.ମି.
PR – PQ = 11 ସେ.ମି. – 8 ସେ.ମି. = 3 ସେ.ମି.
(ଗ) QR, 3 ସେ.ମି. ଠାରୁ ଅଧୁକ ଓ 19 ସେ.ମି ଠାରୁ ସାନ ଉକ୍ତିଟି ଠିକ୍ ଉକ୍ତି ।
