Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 3 ମୌଳିକ ଜ୍ୟାମିତିକ ଚିତ୍ର Ex 3.3 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 3 ମୌଳିକ ଜ୍ୟାମିତିକ ଚିତ୍ର Ex 3.3
Question 1.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖ୍ ନିମ୍ନ ପ୍ରଶ୍ନର ଉତ୍ତର ଦିଅ ।
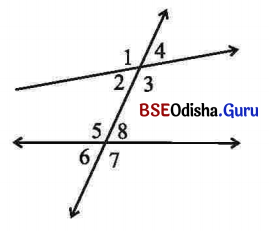
(କ) ∠1 ଓ ∠5 କି ପ୍ରକାର କୋଣ ଯୋଡ଼ି?
ଆଉ ଯେଉଁ କୋଣଗୁଡ଼ିକ ସେହି ପ୍ରକାର, ସେଗୁଡ଼ିକର ନାମ ଲେଖ ।
ସମାଧାନ:
∠1 ଓ ∠5 ଅନୁରୂପ କୋଣ ଯୋଡ଼ି ।
(∠2, ∠6), (∠4, ∠8) ଓ (∠3, ∠7) ମଧ୍ୟ ଅନୁରୂପ କୋଣ ଯୋଡ଼ି ।
(ଖ) 3 ଓ 25 କି ପ୍ରକାର କୋଣ ଯୋଡ଼ି?
ସେହି ପ୍ରକାର ଅନ୍ୟ କୋଣ ଯୋଡ଼ିର ନାମ ଲେଖ।
ସମାଧାନ:
∠3 ଓ ∠5 ଏକାନ୍ତର କୋଣ ଯୋଡ଼ି । ସେହିପରି ∠2 ଓ ∠8 ଏକାନ୍ତର କୋଣ ଯୋଡ଼ି ।
(ଗ) ∠2 ଓ ∠5 କି ପ୍ରକାର କୋଣ ଯୋଡ଼ି ?
ସେହି ପ୍ରକାର ଅନ୍ୟ କୋଣ ଯୋଡ଼ିର ନାମ ଲେଖ
ସମାଧାନ:
∠2 ଓ ∠5 ଛେଦକ ରେଖାର ଏକ ପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୋଣ ଯୋଡ଼ି ।
ସେହିପରି ∠3 ଓ ∠8 ଛେଦକ ରେଖାର ଏକ ପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୋଣ ଯୋଡ଼ି ।
![]()
Question 2.
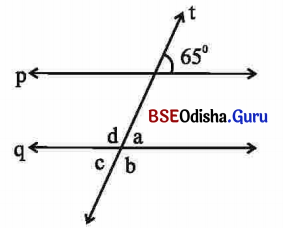
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ସରଳ ରେଖା p || q ଏବଂ ରେଖା t ଏକ ଛେଦକ। ଉତ୍ପନ୍ନ ହେଉଥିବା କୋଣମାନଙ୍କ ମଧ୍ୟରୁ ଗୋଟିଏ କୋଣର ପରିମାଣ 65 ଚିତ୍ରରେ ଦିଆଯାଇଛି । ଅନ୍ୟ ଋରୋଟି କୋଣର ପରିମାଣକୁ a, b, c, d ସଙ୍କେତ ଦ୍ବାରା ଦର୍ଶାଯାଇଛି। a, b, c ଓ d ପ୍ରତ୍ୟେକର ମାନ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
m∠a = 65°, (∵ ଅନୁରୂପ କୋଣ ଯୋଡ଼ି) m∠c = 65° (∵ ∠a ର ପ୍ରତୀପ କୋଣ)
m∠d = 180° – 65° = 115° (∵ ∠a ଓ ∠d ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
m∠b = m∠d = 115° (∵ ∠b ଓ ∠d ପ୍ରତୀପ କୋଣ)
Question 3.
ନିମ୍ନରେ ଥିବା ଚାରିଯୋଡ଼ା ରେଖାମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ ଯୋଡ଼ା ସମାନ୍ତର ଓ କେଉଁ ଯୋଡ଼ା ଅସମାନ୍ତର କହ । ତୁମର ଉତ୍ତର ସପକ୍ଷରେ କାରଣ ଦର୍ଶାଅ ।
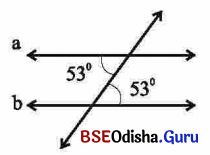
(କ)
ସମାଧାନ:
‘କ’ ଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ ରେଖାଯୋଡ଼ି ସମାନ୍ତର ହେବେ କାରଣ ଏଠାରେ ଏକାନ୍ତର କୋଣ ଯୋଡ଼ିର ପରିମାଣ ସମାନ ।
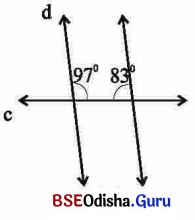
(ଖ)
ସମାଧାନ:
‘ଖ’ ଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ ରେଖାଯୋଡ଼ି ସମାନ୍ତର ହେବେ କାରଣ ଏଠାରେ ଛେଦକର ଏକ ପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୌଣଦ୍ୱୟ ପରସ୍ପର ପରିପୂରକ ।
(ଗ)
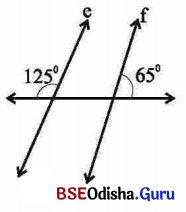
ସମାଧାନ:
‘ଗ’ ଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ ରେଖା e ଓ f ସମାନ୍ତର ହେବେ ନାହିଁ, କାରଣ 125° + 65° ≠ 180°
(ଘ)
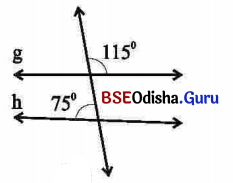
ସମାଧାନ:
‘ଘ’ ଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ g ଓ h ରେଖା ସମାନ୍ତର ହେବେ ନାହିଁ ।
କାରଣ 115° + 75° ≠ 180°
Question 4.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ସରଳରେଖା ℓ || m ଏବଂ ସରଳରେଖା p || q | ଚିତ୍ରରେ ଥିବା ଗୋଟିଏ କୋଣର ପରିମାଣ 75° ଦିଆଯାଇଛି । ଅନ୍ୟ ତିନୋଟି କୋଣର ପରିମାଣକୁ a, b, c ସଙ୍କେତ ଦ୍ଵାରା ସୂଚିତ କରାଯାଇଛି । a, b ଓ c ର ମାନ ନିର୍ଣ୍ଣୟ କର ।
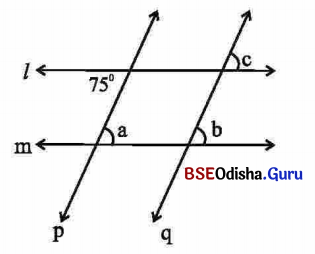
ସମାଧାନ:
m∠a = 75° (∵ ଏକାନ୍ତର କୋଣ), m∠b= m∠a = 75° (∵ ଅନୁରୂପ କୋଣ)
m∠c = m∠b = 75° (∵ ଅନୁରୂପ କୋଣ)
![]()
Question 5.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଭଳି 60° ପରିମାଣ ବିଶିଷ୍ଟ ∠ABC ଅଙ୍କନ କରି \(\overrightarrow{\mathrm{BC}}\) ଉପରେ ଏକ ବିନ୍ଦୁ ଚିହ୍ନଟ କର, ତା’ର ନାମ ଦିଅ D D ବିନ୍ଦୁରେ \(\overleftrightarrow{\mathrm{DE}}\) (ଚିତ୍ରରେ ଦର୍ଶାଯାଇଥିବା ଭଳି) ଅଙ୍କନ କର ଯେପରି \(\overrightarrow{\mathrm{DE}}\) ॥ \(\overrightarrow{\mathrm{BA}}\) ହେବ । ଏହି କାର୍ଯ୍ୟ ଲାଗି ∠BDB କୋଣର ପରିମାଣ କେତେ ନେଇ \(\overrightarrow{\mathrm{DE}}\) ଅଙ୍କନ କରିବ ? କାରଣ ଲେଖ ।
ସମାଧାନ:
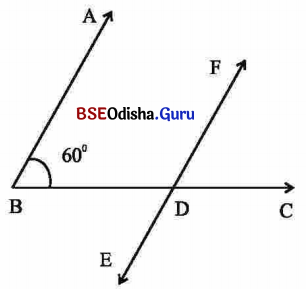
m∠BDE = 60° (ଦତ୍ତ)
କିନ୍ତୁ m∠ABD ଓ m∠BDE ଏକାନ୍ତର ଯୋଡ଼ି କୋଣ ।
m∠ABD = m∠BDE = 60° ⇒ \(\overrightarrow{\mathrm{BA}}\) || \(\overrightarrow{\mathrm{DE}}\)
ତେଣୁ m∠BDE = 60° ନେଇ \(\overrightarrow{\mathrm{DE}}\) ଅଙ୍କନ କରାଯିବ ।
