BSE Odisha 8th Class Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(c)

Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(c)

Question 1.
5 ଜଣ ଶ୍ରମିକ 8 ଦିନରେ 1600 ଟଙ୍କା ରୋଜଗାର କରନ୍ତି; ତେବେ 8 ଜଣ ଶ୍ରମିକ କେତେ ଦିନରେ 2000 ଟଙ୍କା ରୋଜଗାର କରିବେ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ପାରିଶ୍ରମିକର ପରିମାଣ ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ପ୍ରତିଲେ।ମା ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ, ହେବେ । ଅର୍ଥାତ୍‌ y ∝ \(\frac { 1 }{ x }\) (z ସ୍ଥିର) …(i)
ଶ୍ରମିକ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ପାରିଶ୍ରମିକର ପରିମାଣ ସଳଖ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ,
Y ∝ z (x ସ୍ଥିର) …(ii)

Egⁿ. (i) ଓ Eqⁿ. (ii) ରୁ ଯୌଥ ଚଳନ ଅନୁସାରେ y ∝ \(\frac { z }{ x }\) …(iii)
Eqⁿ.(iii) ରୁ ପାଇବା \(\frac{\mathrm{y}_1}{\mathrm{y}_2}\) = \(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) × \(\frac{\mathrm{x}_2}{\mathrm{x}_1}\) ⇒ \(\frac{8}{y_2}\) = \(\frac{1600}{2000}\) × \(\frac{8}{5}\) ⇒ y₂ = \(=\frac{8 \times 2000 \times 5}{8 \times 1600}\) ⇒ y₂ = \(\frac{25}{4}\) ବା 6\(\frac{1}{4}\) ଦିନ
∴ 8 ଜଣ ଶ୍ରମିକ 6\(\frac{1}{4}\) ଦିନରେ 2000 ଟଙ୍କା ରୋଜଗାର କରିବେ ।

Question 2.
10 ଜଣ ଶ୍ରମିକ 6 ଦିନରେ ଗୋଟିଏ ଘର ତିଆରି କରନ୍ତି । ଏକାପରି 4ଟି ଘରକୁ 12 ଜଣ କେତେ ଦିନରେ ଶେଷକରିବେ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶ କଲେ,

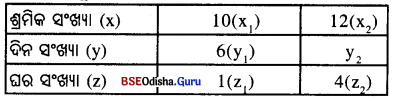
ଏଠାରେ ଘର ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ଶ୍ରମିକ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
ଅର୍ଥାତ୍ y ∝\(\frac { 1 }{ x }\) (z ସ୍ଥିର) … (i)
ଶ୍ରମିକ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ଘର ସଂଖ୍ୟାର ପରିମାଣ ସଳଖ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବ । ଅର୍ଥାତ୍‌ y ∝ z (x ସ୍ଥିର) …(ii)
(i) ଓ (ii) ରୁ ଯୌଥଚଳନ ଅନୁସାରେ y ∝\(\frac { z }{ x }\) … (i)
(iii) ରୁ ପାଇବା \(\frac{\mathrm{y}_1}{\mathrm{y}_2}\) = \(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) × \(\frac{\mathrm{x}_2}{\mathrm{x}_1}\) ⇒ \(\frac{6}{y_2}\) = \(\frac { 1 }{ 4 }\) × \(\frac { 12 }{ 10 }\) ⇒ y₂ = \(\frac{6 \times 4 \times 10}{12}\) = 20
∴ 4 ଟି ଘରକୁ 12 ଜଣ ଶ୍ରମିକ 20 ଦିନରେ ଶେଷକରିବେ ।

Question 3.
12 ଜଣ ଶ୍ରମିକ 15 ଦିନରେ 150 ମିଟର ରାସ୍ତା ତିଆରି କରି ପାରନ୍ତି; ତେବେ 18 ଜଣ ଶ୍ରମିକ କେତେ ଦିନରେ 300 ମିଟର ରାସ୍ତା ତିଆରିକରିବେ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ରାସ୍ତାର ଲମ୍ବ ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ଶ୍ରମିକ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
ଅର୍ଥାତ୍ y ∝\(\frac { 1 }{ x }\) (z ସ୍ଥିର) … (i)
ଶ୍ରମିକ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ରାସ୍ତାର ଦୈର୍ଘ୍ୟର ପରିମାଣ ସଳଖ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବ । Y ∝ z (x ସ୍ଥିର) …(ii)
Eqⁿ (i) ଓ Eqⁿ. (ii) ରୁ ଯୌଥ ଚଳନ ଅନୁସାରେ y ∝ \(\frac { z }{ x }\) …(iii)
Eqⁿ. (iii) ରୁ ପାଲଦା \(\frac{\mathrm{y}_1}{\mathrm{y}_2}\) = \(\frac{\mathrm{z}_1}{\mathrm{y}_2}\) × \(\frac{\mathrm{x}_2}{\mathrm{x}_1}\) ⇒ \(\frac{15}{\mathrm{y}_2}\) = \(\frac { 150 }{ 300 }\) × \(\frac { 18 }{ 12 }\) ⇒ y₂ = \(\frac{15 \times 300 \times 12}{150 \times 18}\) = 20
∴ 18 ଜଣ ଶ୍ରମିକ 20 ଦିନରେ 300 ମିଟର ରାସ୍ତା ତିଆରିକରିବେ ।

Question 4.
10 ଜଣ ପରୀକ୍ଷକ 8 ଦିନରେ 2000 ଖାତା ଦେଖାରନ୍ତି । ତେବେ 12 ଜଣ ପରୀକ୍ଷକ କେତେ ଦିନରେ 3000 ଖାତା ଦେଖପାରିବେ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଖାତା ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ପରୀକ୍ଷକ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
ଅର୍ଥାତ୍ y ∝\(\frac { 1 }{ x }\) (z ସ୍ଥିର) … (i)
ପରୀକ୍ଷକ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ଖାତା ସଂଖ୍ୟା ସଳଖ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବ ।
ଅର୍ଥାତ୍, y ∝ z (x ସ୍ଥିର) …(ii)
Eqⁿ. (i) ଓ Eqⁿ. (ii) ରୁ ଯୌଥ ଚଳନ ଅନୁସାରେ, y ∝\(\frac { z }{ x }\) (z ସ୍ଥିର) … (iii)
Egⁿ. (iii) ରୁ ପାଇବା \(\frac{\mathrm{y}_1}{\mathrm{y}_2}\) = \(\frac{\mathrm{z}_1}{\mathrm{y}_2}\) × \(\frac{\mathrm{x}_2}{\mathrm{x}_1}\) ⇒ \(\frac{8}{\mathrm{y}_2}\) = \(\frac { 2000 }{ 3000 }\) × \(\frac { 12 }{ 10 }\) ⇒ y₂ = \(\frac{8 \times 3000 \times 10}{2000 \times 12}\) = 10
∴12 ଜଣ ପରୀକ୍ଷକ 10 ଦିନରେ 3000 ଖାତା ଦେଖିପାରିବେ ।

Question 5.
6 ଜଣ ଲୁଗାବୁଣାଳୀ 8 ଦିନରେ 144 ମିଟର ଲୁଗା ବୁଣିପାରନ୍ତି । 12 ଜଣ ଲୁଗାବୁଣାଳୀ 9 ଦିନରେ କେତେ ମିଟର ଲୁଗା ବୁଣିପାରିବେ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଦିନ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଲୁଗାର ଦୈର୍ଘ୍ୟ ଓ ଲୋକ ସଂଖ୍ୟା ସଳଖ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
ଅର୍ଥାତ୍ z ∝ x (y ସ୍ଥିର) … (i)
ଲୋକ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଲୁଗାର ଦୈର୍ଘ୍ୟ ଓ ଦିନସଂଖ୍ୟା ସଳଖ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବ ।
ଅର୍ଥାତ୍, z ∝ y (x ସ୍ଥିର) … (ii)
Egⁿ. (i) ଓ Eqⁿ. (ii) ରୁ ଯୌଥ ଚଳନ ଅନୁସାରେ,
z ∝ xy … (iii)
Eqⁿ. (iii) ରୁ ପାଇବା \(\frac{\mathrm{z}_1}{\mathrm{z}_2}\) = \(\frac{x_1 y_1}{x_2 y_2}\) ⇒ \(\frac{144}{z_2}\) = \(\frac{6 \times 8}{12 \times 9}\) ⇒ z₂ = \(\frac{144 \times 12 \times 9}{6 \times 8}\) = 324
∴ 12 ଜଣ ଲୁଗାବୁଣାଳୀ 9 ଦିନରେ 324 ମିଟର ଲୁଗା ବୁଣିପାରିବେ ।

Question 6.
8 ଜଣ ଦରଜି 12 ଦିନରେ 360ଟି ସାର୍ଟ ତିଆରି କରି ପାରନ୍ତି । 15 ଦିନରେ 450ଟି ସାର୍ଟ ତିଆରିପାଇଁ କେତେ ଜଣ ଦରଜି ଆବଶ୍ୟକ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ସାର୍ଟ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦରଜି ସଂଖ୍ୟା ଓ ଦିନ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
ଅର୍ଥାତ୍ x ∝ \(\frac { 1 }{ y }\) (z ସ୍ଥିର) … (i)
ଦିନ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦରଜି ସଂଖ୍ୟା ଓ ସାର୍ଟ ସଂଖ୍ୟା ସଳଖ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ।
ଅର୍ଥାତ୍, x ∝ z (y ସ୍ଥିର) … (ii)
Eqⁿ. (i) ଓ Eq”. (ii) ରୁ ଯୌଥ ଚଳନ ଅନୁସାରେ, x ∝ \(\frac { z }{ y }\) … (iii)
Eqⁿ. (iii) ରୁ ପାଇବା \(\frac{x_1}{x_2}\) = \(\frac{z_1}{z_2}\) × \(\frac{y_2}{y_1}\) ⇒ \(\frac{8}{x_2}\) = \(\frac{360}{450}\) × \(\frac{15}{12}\) ⇒ x₂ = \(\frac{12 \times 450 \times 8}{15 \times 360}\) = 8
∴ 15 ଦିନରେ 450ଟି ସାର୍ଟ ତିଆରି ପାଇଁ 8 ଜଣ ଦରଜି ଆବଶ୍ୟକ ।

Question 7.
2ଟି ପାଣିପମ୍ପ 5 ଘଣ୍ଟାରେ 3ଟି କୁଣ୍ଡର ପାଣି ଟାଣିପାରନ୍ତି; ତେବେ 4ଟି ପାଣିପମ୍ପ କେତେ ଘଣ୍ଟାରେ ସେହି ଆକାରର 12ଟି କୁଣ୍ଡର ପାଣି ଟାଣିପାରିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

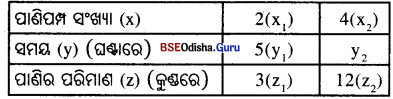
ଏଠାରେ ପାଣିର ପରିମାଣ ସ୍ଥିର ରହିଲେ, ସମୟ ଓ ପାଣିପମ୍ପ ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
y ∝ \(\frac { 1 }{ y }\) (z ସ୍ଥିର) … (i)
ପାଣିପମ୍ପ ସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ସମୟ ଓ ପାଣିର ପରିମାଣ ସଳଖ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
Y ∝ z (x ସ୍ଥିର) … (ii)
Eqⁿ. (i) ଓ Eqⁿ. (ii) ରୁ ଯୌଥ ଚଳନ ଅନୁସାରେ, y ∝ \(\frac { z }{ x }\) … (iii)
Eqⁿ. (iii) ରୁ ପାଇବା \(\frac{y_1}{y_2}\) = \(\frac{z_1}{z_2}\) × \(\frac{x_2}{x_1}\) ⇒ \(\frac{5}{y_2}\) = \(\frac{3}{12}\) × \(\frac{4}{2}\) ⇒ y₂ = \(\frac{5 \times 12 \times 2}{3 \times 4}\) = 10
∴ 4ଟି ପାଣିପମ୍ପ 10 ଘଣ୍ଟାରେ ସେହି ଆକାରର 12ଟି କୁଣ୍ଡର ପାଣି ଟାଣିପାରିବେ ।

Question 8.
ଗୋଟିଏ କାର୍ଯ୍ୟକୁ 25 ଜଣ ଲୋକ ଦୈନିକ 6 ଘଣ୍ଟା ପରିଶ୍ରମ କରି 18 ଦିନରେ ଶେଷକରନ୍ତି । ସେହି କାର୍ଯ୍ୟଟିକୁ 20 ଜଣ ଲୋକ ଦୈନିକ 5 ଘଣ୍ଟା ପରିଶ୍ରମ କରି କେତେ ଦିନରେ ଶେଷକରିବେ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଲୋକସଂଖ୍ୟା ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ସମୟ ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
z ∝ \(\frac { 1 }{ y }\) (x ସ୍ଥିର) … (i)
ସମୟ ସ୍ଥିର ରହିଲେ, ଦିନ ସଂଖ୍ୟା ଓ ଲୋକସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ହେବେ ।
Z ∝ \(\frac { 1 }{ x }\) (y ସ୍ଥିର) … (ii)
ଯୌଥ ଚଳନ ଅନୁଯାୟୀ Egⁿ. (i) ଓ Eqⁿ. (ii) ରୁ ପାଇବା,
Z ∝ \(\frac { 1 }{ xy }\) (x ଓ y ଉଭୟେ ପରିବର୍ତ୍ତନଶୀଳ) … (iii)
Eqⁿ. (iii) ରୁ ପାଇବା \(\frac{z_1}{z_2}\) = \(\frac{x_2}{x_1}\) × \(\frac{y_2}{y_1}\) ⇒ \(\frac{18}{z_2}\) = \(\frac{20 \times 5}{25 \times 6}\) ⇒ z₂ = \(\frac{18 \times 25 \times 6}{20 \times 5}\) ⇒ z₂ = 27
∴ 27 ଦିନରେ 20 ଜଣ ଲୋକ ଦିନକୁ 5 ଘଣ୍ଟା ପରିଶ୍ରମ କରି କାର୍ଯ୍ୟଟି ଶେଷ କରି ପାରିବେ ।