CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Exercise 3(b)

Question 1.
Maximize Z = 5x₁+ 6x₂
Subject to: 2x₁ + 3x₂ ≤ 6
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraint as equation, we get 2x₁ + 3x₂ = 6
Step – 2 Let us draw the graph

x₁	3	0
x₂	0	0

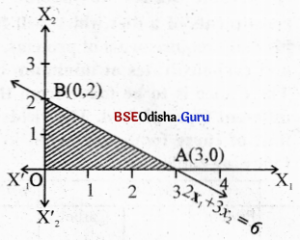
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.1$
Step – 3 Clearly (0,0) statisfies 2x₁ + 3x₂ ≤ 6
The shaded region is the feasible region with vertices 0(0,0), A(3,0), B(0,2).
Step – 4

Corner point	Z = 5x₁+ 6x₂
0(0.0)	0
A(3,0)	15 → maximum
B(0,2)	12

Z is maximum at A (3,0)
∴ The solution of LPP is x₁ = 3, x₂ = 0
Z_max = 15

Question 2.
Minimize: Z = 6x₁ + 7x₂
Subject to: x₁ + 2x₂ ≥ 4
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraint as equation we get x₁ + 2x₂ = 0
Step – 2 Let us draw the graph of x₁ + 2x₂ = 4

x₁	0	4
x₂	2	0

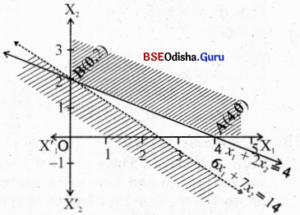
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.2$
Step – 3 Clearly 0(0,0) does not satisfy
x₁ + 2x₂ > 4, x₁> 0, x₂> 0 is the first quadrant.
The feasible region is the shaded region with vertices A(4, 0), B(0, 2).
Step – 4 Z (4, 0) = 24
Z (0, 2) = 14 → minimum
Step – 5 As the feasible region is unbounded we cannot immediately decide Z is minimum at B (0, 2).
Let us draw the half-plane 6x₁ + 7x₂ < 14

x₁	0	3.5
x₂	2	-1

As this half-plane has no point common with the feasible region, we have Z is minimum for x₁= 0, x₂ = 2 and the minimum value of Z = 14.

Question 3.
Maximize Z = 20x₁+ 40x₂
Subject to: x₁ + x₂ ≤ 1
6x₁ + 2x₂ ≤ 3
x₁, x₂ ≥ 0.
Solution:
Step – 1 Treating the constraints as equations
x₁ + x₂ = 1 …. (1)
6x₁ + 2x₂ = 3 …. (2)
x₁, x₂ ≥ 0
Step – 2 Let us draw the graph:
Table – 1

x₁	0	1
x₂	1	0

Table – 2

x₁	0	0.5
x₂	1.5	0

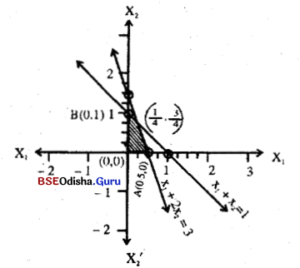
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.3$
Step – 3 As (0, 0) satisfies both the inequations the shaded region is the feasible region.
Step – 4 Solving
x₁ + x₂ = 1
6x₁ + 2x₂ = 3
we have x₁ = ¼ x₂ = ¾
The vertices are O(0, 0), A(0.5, 0), B(0,1) and C(¼, ¾)
Now Z(O) = 0
Z(A) = 10
Z(B) = 40
Z(C) = 20 × ¼ + 40 × ¾ = 35
∴ Z attains maximum at B for x₁= 0, x₂ = 1
Z_max = 40

Question 4.
Minimize: Z = 30x₁ + 45x₂
Subject to: 2x₁ + 6x₂ ≥ 4
5x₁ + 2x₂ ≥ 5
x₁, x₂ ≥ 0
Solution:
Step – 1 Consider the constraints as equations
2x₁ + 6x₂ = 4
5x₁ + 2x₂ = 5
Step – 2
Table – 1

x₁	2	-1
x₂	0	1

Table – 2

x₁	1	0
x₂	0	2.5

Step – 3 Clearly 0(0,0) does not satisfy 2x₁ + 6x₂ ≥ 4 and 5x₁ + 2x₂ ≥ 5.
Thus the shaded region is the feasible region.
Solving the equations we get
x₁ = $\frac{11}{13}$, x₂ = $\frac{5}{13}$.
∴ The vertices are A(2, 0)
B($\frac{11}{13}$, $\frac{5}{13}$) and C(0, $\frac{5}{2}$).
Step – 4 Z(A) = 60
Z(B) = $\frac{555}{13}$ → minimum
Z(C) = $\frac{225}{2}$
Step – 5 As the feasible region is unbounded we cannot immediately decide Z is minimum at B($\frac{11}{13}$, $\frac{5}{13}$)
Let us draw the half plane
30x₁ + 45x₂ < $\frac{555}{13}$

x₁	$\frac{11}{13}$	0
x₂	$\frac{5}{13}$	$\frac{27}{39}$

As this half plane and the feasible region has no point in common we have Z is minimum for x₁ = $\frac{11}{13}$, x₂ = $\frac{5}{13}$, and Z_min = $\frac{555}{13}$

Question 5.
Maximize: Z = 3x₁+ 2x₂
Subject to: -2x₁ + x₂ ≤ 1
x₁ ≤ 2
x₁+ x₂ ≤ 3
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraints as equations
-2x₁ + x₂ = 1 …..(1)
x₁ = 2 …..(2)
x₁+ x₂ = 3 …..(3)
Step – 2 Let us draw the lines.
Table – 1

x₁	0	-1
x₂	1	-1

Table – 2

x₁	2	2
x₂	0	1

Table – 3

x₁	0	3
x₂	3	0

Step – 3 (0, 0) satisfies all the constraints and x₁, x₂ > 0 is the 1st quadrant the shaded region is the feasible region.
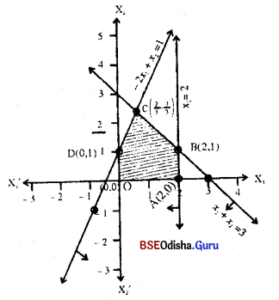
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.5$
Step – 4 Solving -2x₁ + x₂ = 1
x₁+ x₂ = 3
we have 3x₁ = 2
⇒ x₁ = $\frac{2}{3}$, x₂ = 3 – $\frac{2}{3}$ = $\frac{7}{3}$
From x₁+ x₂ = 3 and x₁ = 2 we have x₁ = 2, x₂ = 1
∴ The vertices are 0(0, 0), A(2, 0), B(2, 1), C($\frac{2}{3}$, $\frac{7}{3}$), D(0, 1)
Z(0) = 0, Z(A) = 6, Z(B) = 8, Z(C) = 3.$\frac{2}{3}$ + 2.$\frac{7}{3}$ = $\frac{20}{3}$, Z(D) = 2
Z is maximum at B.
∴ The solution of given LPP is x₁ = 2, x₂ = 1, Z_(max) = 8.

Question 6.
Maximize: Z = 50x₁+ 60x₂
Subject to: x₁ + x₂ ≤ 5
x₁+ 2x₂ ≤ 4
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x₁ + x₂ = 5 ….(1)
x₁+ 2x₂ = 4 ….(2)
Step – 2 Let us draw the graph
Table – 1

x₁	5	5
x₂	0	0

Table – 2

x₁	4	0
x₂	0	2

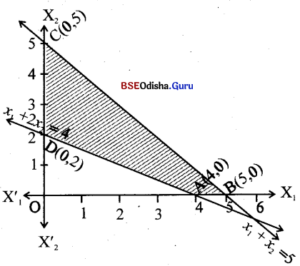
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.6$
Step – 3 0(0,0) satisfies x₁ + x₂ ≤ 5 and does not satisfy x₁+ 2x₂ ≤ 4
Thus the shaded region is the feasible region.
Step – 4 The corner points are A(4,0), B(5,0), C(0,5) , D(0,2)
∴

Corner point	z = 50x₁+ 60x₂
A(4,0)	200
B (5,0)	250 → maximum
C(0,5)	300
D(0,2)	120

Z is maximum for x₁ = 0, x₂ = 5, Z_(max) = 300.

Question 7.
Maximize: Z = 5x₁+ 7x₂
Subject to: x₁ + x₂ ≤ 4
5x₁+ 8x₂ ≤ 30
10x₁+ 7x₂ ≤ 35
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get,
x₁ + x₂ = 4 …. (1)
5x₁+ 8x₂ = 30 …. (2)
10x₁+ 7x₂ = 35 …. (3)
Step – 2 Let us draw the graph
Table – 1

x₁	4	0
x₂	0	4

Table – 2

x₁	6	2
x₂	0	2.5

Table – 3

x₁	0	3.5
x₂	5	0

Step – 3 0(0,0) satisfies all the constraints.
Thus the shaded region is the feasible region.
From (1) and (2) we get ($\frac{2}{3}$, $\frac{10}{3}$)
From (1) and (3) we get
x₁ = $\frac{7}{3}$, x₁ = $\frac{5}{3}$
∴ The corner points are 0(0,0), A($\frac{7}{2}$, 0), B($\frac{7}{3}$, $\frac{5}{3}$), C($\frac{2}{3}$, $\frac{10}{3}$), D(0, $\frac{15}{4}$)
Step – 4

Corner point	z = 5x₁+ 7x₂
0(0,0)	0
A($\frac{7}{2}$, 0)	$\frac{35}{2}$
B($\frac{7}{3}$, $\frac{5}{3}$)	$\frac{70}{3}$
C($\frac{2}{3}$, $\frac{10}{3}$)	$\frac{80}{3}$
D(0, $\frac{15}{4}$)	$\frac{105}{4}$

Z attains its maximum value $\frac{80}{3}$ for x₁ = $\frac{2}{3}$ and x₂ = $\frac{10}{3}$.

Question 8.
Maximize: Z = 14x₁ – 4x₂
Subject to: x₁ + 12x₂ ≤ 65
7x₁– 2x₂ ≤ 25
2x₁+ 3x₂ ≤ 10
x₁, x₂ ≥ 0
Also find two other points which maximize Z.
Solution:
Step – 1 Treating the constraints as equations we get
x₁ + 12x₂ = 65 …. (1)
7x₁– 2x₂ = 25 …. (2)
2x₁+ 3x₂ = 10 …. (3)
Step – 2 Let us draw the graph
Table – 1

x₁	65	5
x₂	0	5

Table – 2

x₁	5	10
x₂	5	22.5

Table – 3

x₁	5	2
x₂	0	2

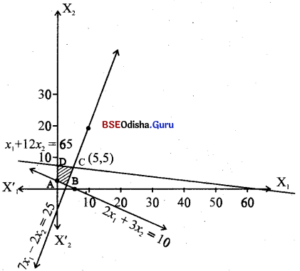
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.8$
Step – 3 Clearly 0(0,0) satisfies x₁ + 12x₂ ≤ 65 and 7x₁– 2x₂ ≤ 25 but does not satisfy 2x₁+ 3x₂ ≤ 10. Thus shaded region is the feasible region.
Equation (1) and (2) meet at (5, 5).
From (2) and (3)
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.8.1$
∴ The corner points of the feasible region are A(0, $\frac{10}{3}$), B($\frac{19}{5}$, $\frac{4}{5}$), C(5, 5), D(0, $\frac{65}{12}$).
Step – 4

Corner point	z = 14x₁ – 4x₂
A(0, $\frac{10}{3}$)	$\frac{-40}{3}$
B($\frac{19}{5}$, $\frac{4}{5}$)	50 → maximum
C(5, 5)	50 → maximum
D(0, $\frac{65}{12}$)	$\frac{65}{3}$

Z is maximum for x₁ = $\frac{19}{5}$, x₂ = $\frac{4}{5}$ or x₁ = 5, x₂ = 5 and Z_max = 50
There is no other point that maximizes Z.

Question 9.
Maximize: Z = 10x₁ + 12x₂ + 8x₃
Subject to: x₁ + 2x₂ ≤ 30
5x₁– 7x₃ ≤ 12
x₁ + x₂ + x₃ = 20
x₁, x₂ ≥ 0
[Hints: Eliminate x₃ from all expressions using the given equation in the set of constraints, so that it becomes an LPP in two variables]
Solution:
Eliminating x₃ this LPP can be written as Maximize Z = 2x₁ + 4x₂ + 160
Subject to: x₁ + 2x₂ ≤ 30
5x₁– 7x₃ ≤ 12
x₁, x₂ ≥ 0
Step – 1 Treating the consraints as equations we get
x₁ + 2x₂ = 30 …..(1)
5x₁– 7x₃ = 12 …..(2)
Step – 2 Let us draw the graph
Table – 1

x₁	30	0
x₂	0	15

Table – 2

x₁	8	1
x₂	8	20

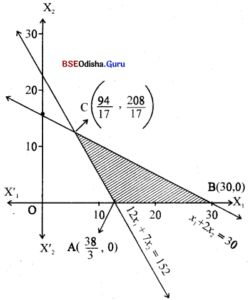
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.9$
Step – 3 Clearly 0(0,0) satisfies x₁ + 2x₂ ≤ 30 and does not satisfy 12x₁ + 7x₂ ≤ 152
∴ The shaded region is the feasible region.
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.9.1$
Step – 4
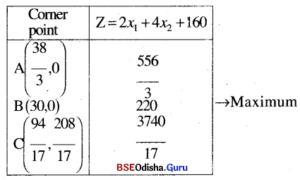
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.9.2$
Z is maximum for x₁ = 30, x₂ = 0 and Z_max = 220

Question 10.
Maximize: Z = 20x₁ + 10x₂
Subject to: x₁ + 2x₂ ≤ 40
3x₁+ x₂ ≥ 30
4x₁+ 3x₂ ≥ 60
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraints as equalities we have:
x₁ + 2x₂ = 40 ….(1)
3x₁+ x₂ = 30 ….(2)
4x₁+ 3x₂ = 60 ….(3)
Step – 2 Let us draw the graph
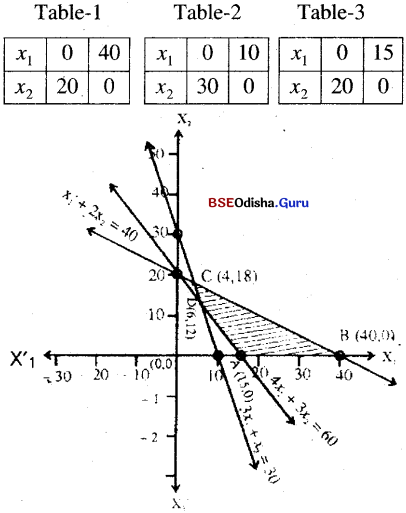
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.10$
Step – 3 (0, 0) satisfies x₁ + 2x₂ ≤ 40 and does not satisfy 3x₁+ x₂ ≥ 30 and 4x₁+ 3x₂ ≥ 60, x₁, x₂ ≥ 0 is the first quadrant.
∴ The shaded region is the feasible region.
Step – 4 x₁ + 2x₂ = 40 and 3x₁+ x₂ = 30
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.10.1$

∴ The vetices are A(15, 0), B(10, 0), C(4, 18) and D(6, 12)
Z(A) = 300, Z(B) = 800
Z (C) = 20 x 4 + 10 x 18 = 260
Z (D) = 120 + 120 = 240
Z attains minimum at D(6 ,12).
∴ The required solution x₁= 6, x₂ =12 and Z_min = 240

Question 11.
Maximize: Z = 4x₁ + 3x₂
Subject to: x₁ + x₂ ≤ 50
x₁+ 2x₂ ≥ 80
2x₁+ x₂ ≥ 20
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraints as equations
x₁ + x₂ ≤ 50 ….(1)
x₁+ 2x₂ ≥ 80 ….(2)
2x₁+ x₂ ≥ 20 ….(3)
Step – 2 Let us draw the graph
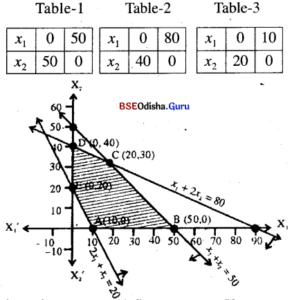
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.11$
Step – 3 (0, 0) satisfies x₁ + x₂ < 50, x₁ + 2x₂ < 80 but does not satisfy
2x₁ + x₂ > 20, x₁ > 0, x₂ > 0 is the 1st quadrant.
Hence the shaded region is the feasible region.
Step – 4 x₁ + x₂ = 50
x₁ + 2x₂ = 80
=> x₂ = 30, x₁ = 20
The vertices of feasible region are
A(10, 0), B(50, 0), C(20, 30), D (0, 40) and E (0, 20)

Point	Z = 4x₁ + 3x₂
A(10,0)	40
5(50,0)	200
C(20,30)	170
D(0,40)	120
E(0,120)	60

Question 12.
Optimize: Z = 5x₁ + 25x₂
Subject to: -0.5x₁ + x₂ ≤ 2
x₁+ x₂ ≥ 2
-x₁+ 5x₂ ≥ 5
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraints as equations
-0.5x₁ + x₂ = 2 ….(1)
x₁+ x₂ = 2 ….(2)
-x₁+ 5x₂ = 5 ….(3)
Step – 2 Let us draw the graph.
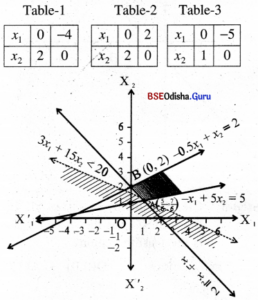
$D:\BSE Odisha.guru\Image\CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.12.png$
Step – 3 (0, 0) satisfies -0.5x₁ + x₂ ≤ 2, but does not satisfy x₁+ x₂ ≥ 2 and -x₁+ 5x₂ ≥ 5, x₁ > 0, x₂ > 0 is the 1st quadrant.
The shaded region is the feasible region with vertices A($\frac{5}{6}$, $\frac{7}{6}$) and B(0, 2).
Step – 4 Z can be made arbitrarily large.
∴ Problem has no maximum.
But Z(A) = $\frac{100}{3}$, Z(B) = 50
Z is minimum at A($\frac{5}{6}$, $\frac{7}{6}$).
But the feasible region is unbounded.
Hence we cannot immediately decide, Z is minimum at A.
Let us draw the half plane
5x₁ + 25x₂ < $\frac{100}{3}$
⇒ 3x₁+ 15x₂ < 20
As there is no point common to this half plane and the feasible region.
we have Z is minimum for x₁ = $\frac{5}{6}$, x₂ = $\frac{7}{6}$ and the minimum value = $\frac{100}{3}$

Question 13.
Optimize: Z = 5x₁ + 2x₂
Subject to: -0.5x₁ + x₂ ≤ 2
x₁+ x₂ ≥ 2
-x₁+ 5x₂ ≥ 5
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraints as equations
-0.5x₁ + x₂ = 2 ….(1)
x₁+ x₂ = 2 ….(2)
-x₁+ 5x₂ = 5 ….(3)
Step – 2 Let us draw the graph.
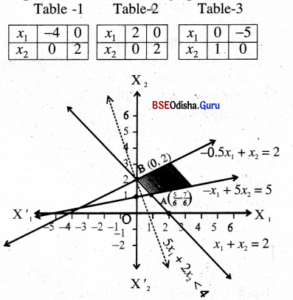
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.13$
Step – 3 The shaded regian is feasible region which is unbounded, thus Z does not have any maximum.
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.13(1)$
As Z can be made arbitrarily large, the given LPP has no maximum.
Z is minimum at B (0, 2). But we cannot immediately decide, Z is minimum at B.
Let us draw the half plane 5x₁ + 2x₂ < 4

x₁	0	4/5
x₂	2	0

As there is no point common to this half plane and the feasible region,
we have Z is minimum for x₁ = 0, x₂ = 2 and the minimum value of Z = 4.

Question 14.
Optimize: Z = -10x₁ + 2x₂
Subject to: -x₁ + x₂ ≥ -1
x₁+ x₂ ≤ 6
x₂ ≤ 5
x₁, x₂ ≥ 0
Solution:
Step – 1 Treating the constraints as equations
-x₁ + x₂ = -1 ….(1)
x₁+ x₂ = 6 ….(2)
x₂ = 5 ….(3)
Step – 2 Let us draw the graph
Table – 1

x₁	1	0
x₂	0	-1

Table – 2

x₁	6	0
x₂	0	1

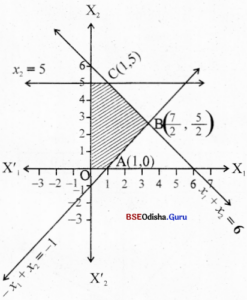
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.14$
Step – 3 Clearly 0(0,0) satisfies all the constraints.
Thus the shaded region is the feasible region.
The vertices are 0(0,0) , A(1,0), B($\frac{7}{2}$, $\frac{5}{2}$) ,C(1, 5) and D (0, 5)
Step – 4 Z(O) = 0
Z(A) = -10
Z(B) = – 30
Z(C) = 0
Z(D) = 10
∴ Z is maximum for x₁= 0, x, = 5 and Z_(max) = 10
Z is minimum for x₁ = $\frac{7}{2}$ x₂ = $\frac{5}{2}$ and Z_(min) = -30

Question 15.
Solve the L.P.P.s obtained in Exercise 3(a) Q.1 to Q. 9 by graphical method.
(1) Maximise: Z = 1500x + 2000y
Subject to: x + y < 20
x + 2y < 24
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x + y = 20
x + 2y = 24
Step – 2 Let us draw of graph.
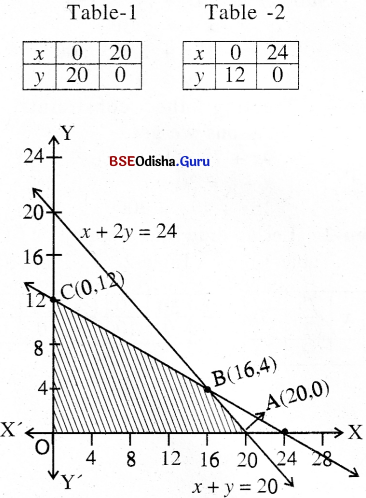
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(1)$
Step – 3 Clearly 0(0,0) satisfies all the constraints.
Thus the shaded region is the feasible region.
From (1) and (2) we get
y = 14
x = 16
With vertices 0(0, 0), A(20, 0), B(16, 4), C(0, 12).
Step – 4 Z(0) = 0
Z(A) = 30,000
Z(B) = 32,000 → Maximum
Z(C) = 24000
Z is maximum for x = 16, y = 4 with Z = 32000
To get maximum profit he must keep 16 sets of model X and 4 sets of model Y.
Maximum profit = 1500 × 16 + 2000 × 4 = ₹32,000

(2) Maximize: 15x + 10y
Subject: x + 3y ≤ 600
2x + y ≤ 480
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
2x +3y = 600
2a + y = 480
Step – 2 Let us draw the graph
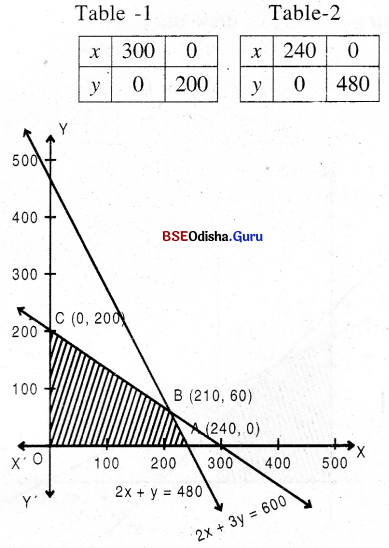
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(2)$
Step – 3 Clearly 0(0,0) satisfies all the constraints.
The corner point are 0(0, 0), A (240, 0) B(210, 60),C(0, 200)
Step – 4 Z(0) = 6
Z(A) = 3600
Z(B) = 3150 + 600
= 3750 → maximum
Z(C) = 2000
Thus Z is maximum for x = 210 and y = 60
and Z_(max) = 3750

(3) Maximize: Z = 20x + 30y
Subject to: x + 2y ≤ 10
x + y ≤ 6
x ≤ 4
x, y ≥ 0.
Solution:
Step – 1 Treating the constraints as equations we get
x + 2y = 10 …(1)
x + y = 6 …(2)
x = 4
Step – 2 Let us draw the graph
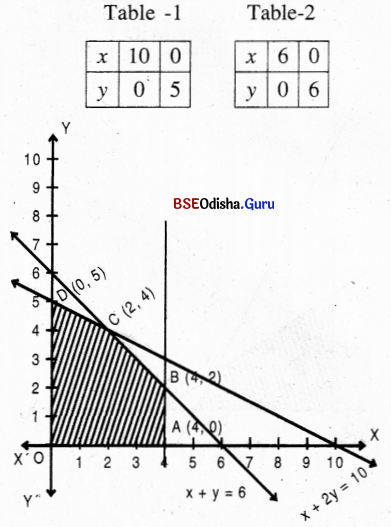
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(3)$
Step – 3 As 0(0,0) satisfies all the constraints the shaded region is the feasible region.
Solving (1) and (2) we get x = 2, y = 4.
The vertices and 0(0, 0) , A(4, 0), B(4, 2), C(2, 4), D (0, 5).
Step – 4 Z(0) =0
Z(A) = 80
Z (B) =140
Z(C) = 1 60 → maximum
Z (D) = 150
∴ Z is Maximum when x = 2, y = 4 and Z_(max) = 160

(4) Maximize: Z = 15x + 17y
Subject to: 4x + 7y ≤ 150
x + y ≤ 30
15x + 17y > 300
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
4x + 7y = 150 ….(1)
x + y = 30 ….(2)
15x + 17y = 300 ….(3)
Step – 2 Let us draw the graph
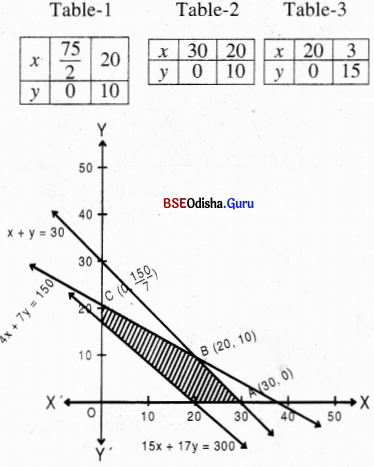
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(4)$
Step – 3 Clearly 0(0,0) satisfies all the constraints.
4x + 7y ≤ 150, x + y ≤ 30, but does not satisfy 15x + 17y ≥ 300.
∴ The shaded region is the feasible region.
From (1) and (2) we get
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(4.1)$
∴ Z is maximum for x = 20. y = 10 and Z_(max) = 470

(5) Maximize: Z = 2x + 4y
Subject to: 3x + 2y ≤ 10
2x + 5y ≤ 15
5x + 6y ≤ 21
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
3x + 2y = 10 …(1)
2x + 5y = 15 …(2)
5x + 6y = 21 …(3)
Step – 2 Let us draw the graph
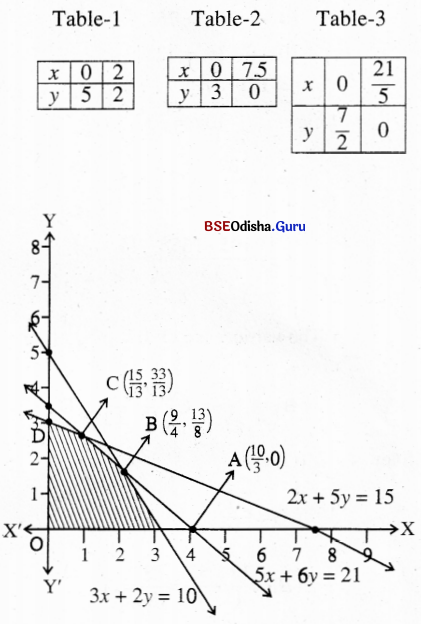
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(5)$
Step – 3 As 0(0,0) satisfies all the constraints the shaded region is the feasible region.
From (1) and (3) we get
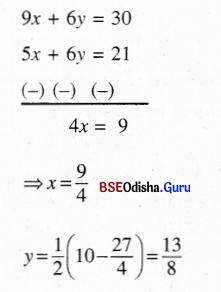
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(5.1)$
From (2) and (3) we get
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(5.2)$
Step-4 Z(O) = 0
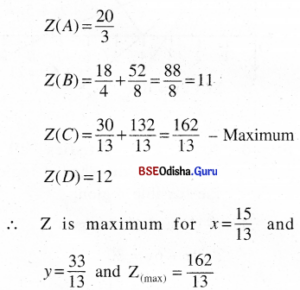
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(5.3)$

(6) Maximize: Z = 1000x + 800y
Subject to: x + y ≤ 5
2x + y ≤ 9
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x + y = 5 ….(1)
2x + y = 9 ….(2)
Step – 2 Let us draw the graph
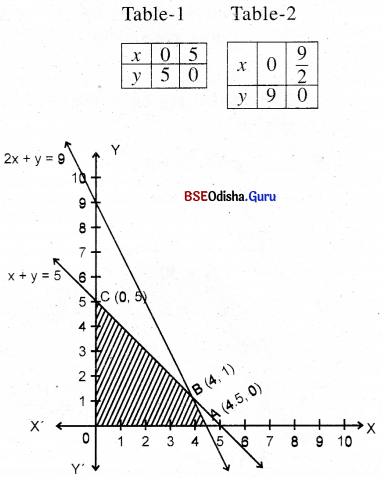
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(6)$
Step – 3 Clearly 0(0,0) satisfies all the constraints.
∴ Thus the shaded region is the feasible region.
From (1) and (2) we get x = 4, y = 1.
∴ The vertices are A(0, 0), A(4.5, 0), B(4, 1) and C(0, 5).
Step – 4 Z(0) =0
Z (A) = 4500
Z (B) = 4800 → Maximum
Z (C) = 4000
Z is maximum for x = 4 and y = 1, Z_(max) = 4800

(7) Minimize: Z = 4960 – 70x – 130y
Subject to: x + y ≤ 12
x + y ≥ 6
x ≤ 8
y ≤ 8
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x + y = 12 ….(1)
x + y = 6 ….(2)
x = 8 ….(3)
y = 4 ….(4)
Step – 2 Let us draw the graph
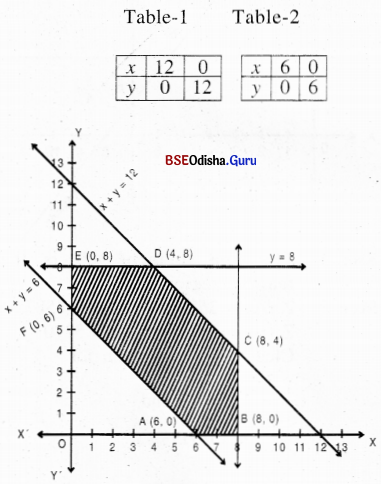
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(7)$

Step – 3 Clearly 0(0,0) satisfies all the constraints except x + y > 6.
The shaded region is the feasible region.
The vertices are A(6, 0), B(8, 0), C(8, 4), D(4, 8), E(0, 8) and F(0, 6).
Step – 4 Z (A) = 4540
Z (B) = 4400
Z (C) = 3880
Z (D) = 3640 → Minimum
Z (E) = 3920
Z (F) = 4180
∴ Z is maximum for x = 4 and y = 8 and Z_(min) = 3640.

(8) Minimize: Z = 16x + 20y
Subject to x + 2y ≥ 10
x + y ≥ 6
3x + y ≥ 8
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x + 2y = 10 ….(1)
x + y = 6 …(2)
3x + y = 8 …(3)
Step – 2 Let us draw the graph
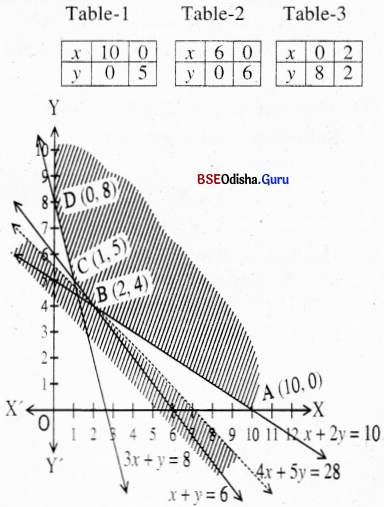
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(8)$
Step – 3 Clearly 0(0,0) satisfies all the constraints. Thus the shaded region is the feasible region.
From (1) and (2) we get y = 4, x = 2.
From (2) and (3) we get x = 1, y = 5.
The vertices are A(10, 0), B(2, 4), C(1, 5), D(0, 8).
Step – 4 Z (A) = 160
Z (B) = 112 → Minimum
Z (C) =116
Z (D) = 160
As the region is unbounded, let us draw the half plane Z < Z_(min)
⇒ 16x + 20y < 112
⇒ 4x + 5y < 28

x₁	7	0
x₂	0	5.6

There is no point common to the shaded region and the half plane 4x + 5y ≤ 28 other than B(2, 4).
∴ Z is minimum for x = 2, y = 4 and Z_(min) = 112.

(9) Minimize: Z = (512.5)x + 800y
Subject to: 5x + 4y = 40
x ≤ 7
x ≤ 3
x, y ≥ 0
Solution:
Step – 1 Let us draw the graph of
5x + 4y = 40
x = 7, y = 3

x₁	8	0
x₂	0	10

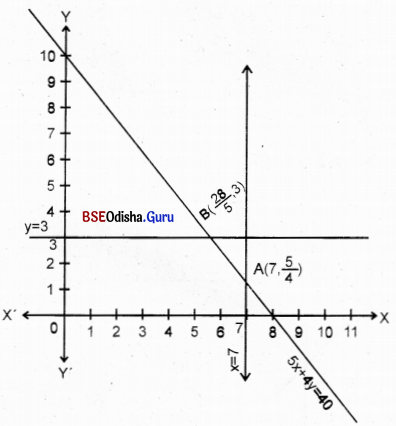
$CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Q.15(9)$
Step – 1 Let us draw the graph of
5x + 4y = 40
x = 7, y = 3
Step – 2 The line segment AB is the feasible region.
Step – 3 Z (A) = 3587.5 + 1000 = 4587.5
Z (B) = 2870 + 2400 = 5270
Clearly Z is minimum for
x = 7, y = $\frac{5}{4}$ and Z_(min) = 4587.5

x₁	\(\frac{11}{13}\)	0
x₂	\(\frac{5}{13}\)	\(\frac{27}{39}\)

Corner point	z = 5x₁+ 7x₂
0(0,0)	0
A(\(\frac{7}{2}\), 0)	\(\frac{35}{2}\)
B(\(\frac{7}{3}\), \(\frac{5}{3}\))	\(\frac{70}{3}\)
C(\(\frac{2}{3}\), \(\frac{10}{3}\))	\(\frac{80}{3}\)
D(0, \(\frac{15}{4}\))	\(\frac{105}{4}\)

CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Exercise 3(b)

Leave a Comment Cancel reply