Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Ex 3(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Exercise 3(b)
Question 1.
Maximize Z = 5x1+ 6x2
Subject to: 2x1 + 3x2 ≤ 6
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraint as equation, we get 2x1 + 3x2 = 6
Step – 2 Let us draw the graph
| x1 | 3 | 0 |
| x2 | 0 | 0 |
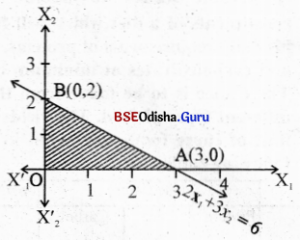
Step – 3 Clearly (0,0) statisfies 2x1 + 3x2 ≤ 6
The shaded region is the feasible region with vertices 0(0,0), A(3,0), B(0,2).
Step – 4
| Corner point | Z = 5x1+ 6x2 |
| 0(0.0) | 0 |
| A(3,0) | 15 → maximum |
| B(0,2) | 12 |
Z is maximum at A (3,0)
∴ The solution of LPP is x1 = 3, x2 = 0
Zmax = 15
Question 2.
Minimize: Z = 6x1 + 7x2
Subject to: x1 + 2x2 ≥ 4
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraint as equation we get x1 + 2x2 = 0
Step – 2 Let us draw the graph of x1 + 2x2 = 4
| x1 | 0 | 4 |
| x2 | 2 | 0 |
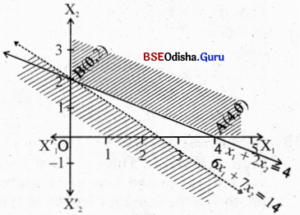
Step – 3 Clearly 0(0,0) does not satisfy
x1 + 2x2 > 4, x1 > 0, x2 > 0 is the first quadrant.
The feasible region is the shaded region with vertices A(4, 0), B(0, 2).
Step – 4 Z (4, 0) = 24
Z (0, 2) = 14 → minimum
Step – 5 As the feasible region is unbounded we cannot immediately decide Z is minimum at B (0, 2).
Let us draw the half-plane 6x1 + 7x2 < 14
| x1 | 0 | 3.5 |
| x2 | 2 | -1 |
As this half-plane has no point common with the feasible region, we have Z is minimum for x1= 0, x2 = 2 and the minimum value of Z = 14.
![]()
Question 3.
Maximize Z = 20x1+ 40x2
Subject to: x1 + x2 ≤ 1
6x1 + 2x2 ≤ 3
x1, x2 ≥ 0.
Solution:
Step – 1 Treating the constraints as equations
x1 + x2 = 1 …. (1)
6x1 + 2x2 = 3 …. (2)
x1, x2 ≥ 0
Step – 2 Let us draw the graph:
Table – 1
| x1 | 0 | 1 |
| x2 | 1 | 0 |
Table – 2
| x1 | 0 | 0.5 |
| x2 | 1.5 | 0 |
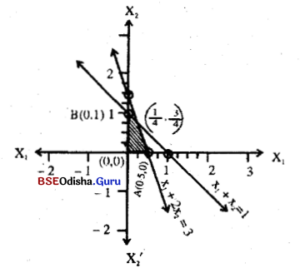
Step – 3 As (0, 0) satisfies both the inequations the shaded region is the feasible region.
Step – 4 Solving
x1 + x2 = 1
6x1 + 2x2 = 3
we have x1 = ¼ x2 = ¾
The vertices are O(0, 0), A(0.5, 0), B(0,1) and C(¼, ¾)
Now Z(O) = 0
Z(A) = 10
Z(B) = 40
Z(C) = 20 × ¼ + 40 × ¾ = 35
∴ Z attains maximum at B for x1= 0, x2 = 1
Zmax = 40
Question 4.
Minimize: Z = 30x1 + 45x2
Subject to: 2x1 + 6x2 ≥ 4
5x1 + 2x2 ≥ 5
x1, x2 ≥ 0
Solution:
Step – 1 Consider the constraints as equations
2x1 + 6x2 = 4
5x1 + 2x2 = 5
Step – 2
Table – 1
| x1 | 2 | -1 |
| x2 | 0 | 1 |
Table – 2
| x1 | 1 | 0 |
| x2 | 0 | 2.5 |
Step – 3 Clearly 0(0,0) does not satisfy 2x1 + 6x2 ≥ 4 and 5x1 + 2x2 ≥ 5.
Thus the shaded region is the feasible region.
Solving the equations we get
x1 = \(\frac{11}{13}\), x2 = \(\frac{5}{13}\).
∴ The vertices are A(2, 0)
B(\(\frac{11}{13}\), \(\frac{5}{13}\)) and C(0, \(\frac{5}{2}\)).
Step – 4 Z(A) = 60
Z(B) = \(\frac{555}{13}\) → minimum
Z(C) = \(\frac{225}{2}\)
Step – 5 As the feasible region is unbounded we cannot immediately decide Z is minimum at B(\(\frac{11}{13}\), \(\frac{5}{13}\))
Let us draw the half plane
30x1 + 45x2 < \(\frac{555}{13}\)
| x1 | \(\frac{11}{13}\) | 0 |
| x2 | \(\frac{5}{13}\) | \(\frac{27}{39}\) |
As this half plane and the feasible region has no point in common we have Z is minimum for x1 = \(\frac{11}{13}\), x2 = \(\frac{5}{13}\), and Zmin = \(\frac{555}{13}\)
Question 5.
Maximize: Z = 3x1+ 2x2
Subject to: -2x1 + x2 ≤ 1
x1 ≤ 2
x1+ x2 ≤ 3
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraints as equations
-2x1 + x2 = 1 …..(1)
x1 = 2 …..(2)
x1+ x2 = 3 …..(3)
Step – 2 Let us draw the lines.
Table – 1
| x1 | 0 | -1 |
| x2 | 1 | -1 |
Table – 2
| x1 | 2 | 2 |
| x2 | 0 | 1 |
Table – 3
| x1 | 0 | 3 |
| x2 | 3 | 0 |
Step – 3 (0, 0) satisfies all the constraints and x1, x2 > 0 is the 1st quadrant the shaded region is the feasible region.
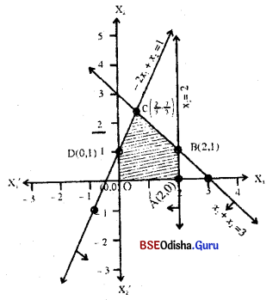
Step – 4 Solving -2x1 + x2 = 1
x1+ x2 = 3
we have 3x1 = 2
⇒ x1 = \(\frac{2}{3}\), x2 = 3 – \(\frac{2}{3}\) = \(\frac{7}{3}\)
From x1+ x2 = 3 and x1 = 2 we have x1 = 2, x2 = 1
∴ The vertices are 0(0, 0), A(2, 0), B(2, 1), C(\(\frac{2}{3}\), \(\frac{7}{3}\)), D(0, 1)
Z(0) = 0, Z(A) = 6, Z(B) = 8, Z(C) = 3.\(\frac{2}{3}\) + 2.\(\frac{7}{3}\) = \(\frac{20}{3}\), Z(D) = 2
Z is maximum at B.
∴ The solution of given LPP is x1 = 2, x2 = 1, Z(max) = 8.
![]()
Question 6.
Maximize: Z = 50x1+ 60x2
Subject to: x1 + x2 ≤ 5
x1+ 2x2 ≤ 4
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x1 + x2 = 5 ….(1)
x1+ 2x2 = 4 ….(2)
Step – 2 Let us draw the graph
Table – 1
| x1 | 5 | 5 |
| x2 | 0 | 0 |
Table – 2
| x1 | 4 | 0 |
| x2 | 0 | 2 |
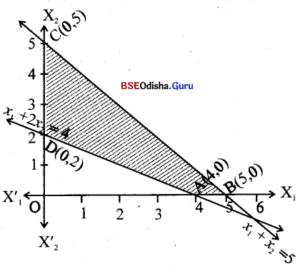
Step – 3 0(0,0) satisfies x1 + x2 ≤ 5 and does not satisfy x1+ 2x2 ≤ 4
Thus the shaded region is the feasible region.
Step – 4 The corner points are A(4,0), B(5,0), C(0,5) , D(0,2)
∴
| Corner point | z = 50x1+ 60x2 |
| A(4,0) | 200 |
| B (5,0) | 250 → maximum |
| C(0,5) | 300 |
| D(0,2) | 120 |
Z is maximum for x1 = 0, x2 = 5, Z(max) = 300.
Question 7.
Maximize: Z = 5x1+ 7x2
Subject to: x1 + x2 ≤ 4
5x1+ 8x2 ≤ 30
10x1+ 7x2 ≤ 35
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get,
x1 + x2 = 4 …. (1)
5x1+ 8x2 = 30 …. (2)
10x1+ 7x2 = 35 …. (3)
Step – 2 Let us draw the graph
Table – 1
| x1 | 4 | 0 |
| x2 | 0 | 4 |
Table – 2
| x1 | 6 | 2 |
| x2 | 0 | 2.5 |
Table – 3
| x1 | 0 | 3.5 |
| x2 | 5 | 0 |
Step – 3 0(0,0) satisfies all the constraints.
Thus the shaded region is the feasible region.
From (1) and (2) we get (\(\frac{2}{3}\), \(\frac{10}{3}\))
From (1) and (3) we get
x1 = \(\frac{7}{3}\), x1 = \(\frac{5}{3}\)
∴ The corner points are 0(0,0), A(\(\frac{7}{2}\), 0), B(\(\frac{7}{3}\), \(\frac{5}{3}\)), C(\(\frac{2}{3}\), \(\frac{10}{3}\)), D(0, \(\frac{15}{4}\))
Step – 4
| Corner point | z = 5x1+ 7x2 |
| 0(0,0) | 0 |
| A(\(\frac{7}{2}\), 0) | \(\frac{35}{2}\) |
| B(\(\frac{7}{3}\), \(\frac{5}{3}\)) | \(\frac{70}{3}\) |
| C(\(\frac{2}{3}\), \(\frac{10}{3}\)) | \(\frac{80}{3}\) |
| D(0, \(\frac{15}{4}\)) | \(\frac{105}{4}\) |
Z attains its maximum value \(\frac{80}{3}\) for x1 = \(\frac{2}{3}\) and x2 = \(\frac{10}{3}\).
Question 8.
Maximize: Z = 14x1 – 4x2
Subject to: x1 + 12x2 ≤ 65
7x1 – 2x2 ≤ 25
2x1+ 3x2 ≤ 10
x1, x2 ≥ 0
Also find two other points which maximize Z.
Solution:
Step – 1 Treating the constraints as equations we get
x1 + 12x2 = 65 …. (1)
7x1 – 2x2 = 25 …. (2)
2x1 + 3x2 = 10 …. (3)
Step – 2 Let us draw the graph
Table – 1
| x1 | 65 | 5 |
| x2 | 0 | 5 |
Table – 2
| x1 | 5 | 10 |
| x2 | 5 | 22.5 |
Table – 3
| x1 | 5 | 2 |
| x2 | 0 | 2 |
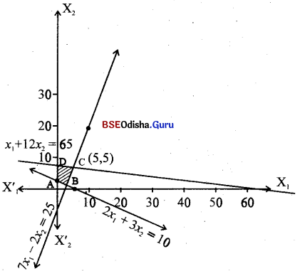
Step – 3 Clearly 0(0,0) satisfies x1 + 12x2 ≤ 65 and 7x1 – 2x2 ≤ 25 but does not satisfy 2x1+ 3x2 ≤ 10. Thus shaded region is the feasible region.
Equation (1) and (2) meet at (5, 5).
From (2) and (3)

∴ The corner points of the feasible region are A(0, \(\frac{10}{3}\)), B(\(\frac{19}{5}\), \(\frac{4}{5}\)), C(5, 5), D(0, \(\frac{65}{12}\)).
Step – 4
| Corner point | z = 14x1 – 4x2 |
| A(0, \(\frac{10}{3}\)) | \(\frac{-40}{3}\) |
| B(\(\frac{19}{5}\), \(\frac{4}{5}\)) | 50 → maximum |
| C(5, 5) | 50 → maximum |
| D(0, \(\frac{65}{12}\)) | \(\frac{65}{3}\) |
Z is maximum for x1 = \(\frac{19}{5}\), x2 = \(\frac{4}{5}\) or x1 = 5, x2 = 5 and Zmax = 50
There is no other point that maximizes Z.
![]()
Question 9.
Maximize: Z = 10x1 + 12x2 + 8x3
Subject to: x1 + 2x2 ≤ 30
5x1 – 7x3 ≤ 12
x1 + x2 + x3 = 20
x1, x2 ≥ 0
[Hints: Eliminate x3 from all expressions using the given equation in the set of constraints, so that it becomes an LPP in two variables]
Solution:
Eliminating x3 this LPP can be written as Maximize Z = 2x1 + 4x2 + 160
Subject to: x1 + 2x2 ≤ 30
5x1 – 7x3 ≤ 12
x1, x2 ≥ 0
Step – 1 Treating the consraints as equations we get
x1 + 2x2 = 30 …..(1)
5x1 – 7x3 = 12 …..(2)
Step – 2 Let us draw the graph
Table – 1
| x1 | 30 | 0 |
| x2 | 0 | 15 |
Table – 2
| x1 | 8 | 1 |
| x2 | 8 | 20 |
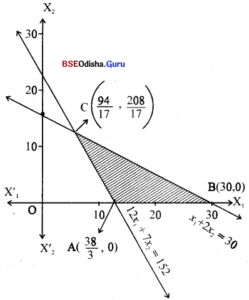
Step – 3 Clearly 0(0,0) satisfies x1 + 2x2 ≤ 30 and does not satisfy 12x1 + 7x2 ≤ 152
∴ The shaded region is the feasible region.

Step – 4
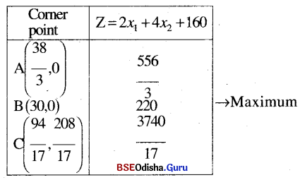
Z is maximum for x1 = 30, x2 = 0 and Zmax = 220
Question 10.
Maximize: Z = 20x1 + 10x2
Subject to: x1 + 2x2 ≤ 40
3x1 + x2 ≥ 30
4x1+ 3x2 ≥ 60
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraints as equalities we have:
x1 + 2x2 = 40 ….(1)
3x1 + x2 = 30 ….(2)
4x1+ 3x2 = 60 ….(3)
Step – 2 Let us draw the graph
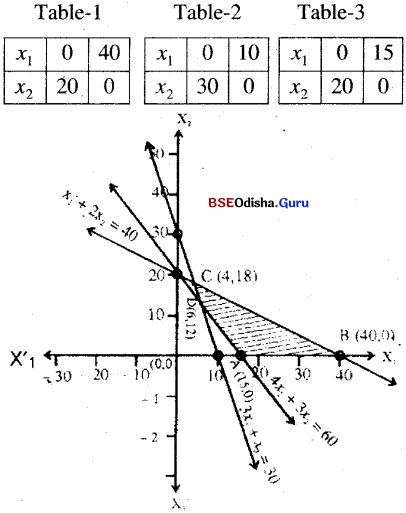
Step – 3 (0, 0) satisfies x1 + 2x2 ≤ 40 and does not satisfy 3x1 + x2 ≥ 30 and 4x1+ 3x2 ≥ 60, x1, x2 ≥ 0 is the first quadrant.
∴ The shaded region is the feasible region.
Step – 4 x1 + 2x2 = 40 and 3x1 + x2 = 30

∴ The vetices are A(15, 0), B(10, 0), C(4, 18) and D(6, 12)
Z(A) = 300, Z(B) = 800
Z (C) = 20 x 4 + 10 x 18 = 260
Z (D) = 120 + 120 = 240
Z attains minimum at D(6 ,12).
∴ The required solution x1 = 6, x2 =12 and Zmin = 240
Question 11.
Maximize: Z = 4x1 + 3x2
Subject to: x1 + x2 ≤ 50
x1 + 2x2 ≥ 80
2x1+ x2 ≥ 20
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraints as equations
x1 + x2 ≤ 50 ….(1)
x1 + 2x2 ≥ 80 ….(2)
2x1+ x2 ≥ 20 ….(3)
Step – 2 Let us draw the graph
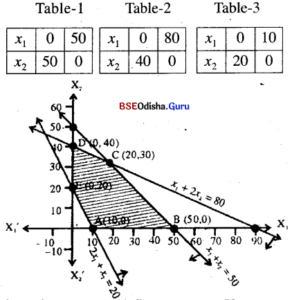
Step – 3 (0, 0) satisfies x1 + x2 < 50, x1 + 2x2 < 80 but does not satisfy
2x1 + x2 > 20, x1 > 0, x2 > 0 is the 1st quadrant.
Hence the shaded region is the feasible region.
Step – 4 x1 + x2 = 50
x1 + 2x2 = 80
=> x2 = 30, x1 = 20
The vertices of feasible region are
A(10, 0), B(50, 0), C(20, 30), D (0, 40) and E (0, 20)
| Point | Z = 4x1 + 3x2 |
| A(10,0) | 40 |
| 5(50,0) | 200 |
| C(20,30) | 170 |
| D(0,40) | 120 |
| E(0,120) | 60 |
![]()
Question 12.
Optimize: Z = 5x1 + 25x2
Subject to: -0.5x1 + x2 ≤ 2
x1 + x2 ≥ 2
-x1+ 5x2 ≥ 5
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraints as equations
-0.5x1 + x2 = 2 ….(1)
x1 + x2 = 2 ….(2)
-x1+ 5x2 = 5 ….(3)
Step – 2 Let us draw the graph.
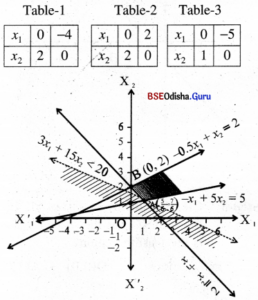
Step – 3 (0, 0) satisfies -0.5x1 + x2 ≤ 2, but does not satisfy x1 + x2 ≥ 2 and -x1+ 5x2 ≥ 5, x1 > 0, x2 > 0 is the 1st quadrant.
The shaded region is the feasible region with vertices A(\(\frac{5}{6}\), \(\frac{7}{6}\)) and B(0, 2).
Step – 4 Z can be made arbitrarily large.
∴ Problem has no maximum.
But Z(A) = \(\frac{100}{3}\), Z(B) = 50
Z is minimum at A(\(\frac{5}{6}\), \(\frac{7}{6}\)).
But the feasible region is unbounded.
Hence we cannot immediately decide, Z is minimum at A.
Let us draw the half plane
5x1 + 25x2 < \(\frac{100}{3}\)
⇒ 3x1 + 15x2 < 20
As there is no point common to this half plane and the feasible region.
we have Z is minimum for x1 = \(\frac{5}{6}\), x2 = \(\frac{7}{6}\) and the minimum value = \(\frac{100}{3}\)
Question 13.
Optimize: Z = 5x1 + 2x2
Subject to: -0.5x1 + x2 ≤ 2
x1 + x2 ≥ 2
-x1+ 5x2 ≥ 5
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraints as equations
-0.5x1 + x2 = 2 ….(1)
x1 + x2 = 2 ….(2)
-x1+ 5x2 = 5 ….(3)
Step – 2 Let us draw the graph.
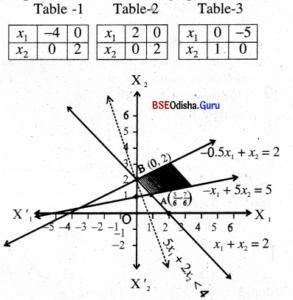
Step – 3 The shaded regian is feasible region which is unbounded, thus Z does not have any maximum.

As Z can be made arbitrarily large, the given LPP has no maximum.
Z is minimum at B (0, 2). But we cannot immediately decide, Z is minimum at B.
Let us draw the half plane 5x1 + 2x2 < 4
| x1 | 0 | 4/5 |
| x2 | 2 | 0 |
As there is no point common to this half plane and the feasible region,
we have Z is minimum for x1 = 0, x2 = 2 and the minimum value of Z = 4.
Question 14.
Optimize: Z = -10x1 + 2x2
Subject to: -x1 + x2 ≥ -1
x1 + x2 ≤ 6
x2 ≤ 5
x1, x2 ≥ 0
Solution:
Step – 1 Treating the constraints as equations
-x1 + x2 = -1 ….(1)
x1 + x2 = 6 ….(2)
x2 = 5 ….(3)
Step – 2 Let us draw the graph
Table – 1
| x1 | 1 | 0 |
| x2 | 0 | -1 |
Table – 2
| x1 | 6 | 0 |
| x2 | 0 | 1 |
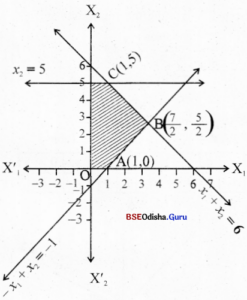
Step – 3 Clearly 0(0,0) satisfies all the constraints.
Thus the shaded region is the feasible region.
The vertices are 0(0,0) , A(1,0), B(\(\frac{7}{2}\), \(\frac{5}{2}\)) ,C(1, 5) and D (0, 5)
Step – 4 Z(O) = 0
Z(A) = -10
Z(B) = – 30
Z(C) = 0
Z(D) = 10
∴ Z is maximum for x1= 0, x, = 5 and Z(max) = 10
Z is minimum for x1 = \(\frac{7}{2}\) x2 = \(\frac{5}{2}\) and Z(min) = -30
![]()
Question 15.
Solve the L.P.P.s obtained in Exercise 3(a) Q.1 to Q. 9 by graphical method.
(1) Maximise: Z = 1500x + 2000y
Subject to: x + y < 20
x + 2y < 24
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x + y = 20
x + 2y = 24
Step – 2 Let us draw of graph.
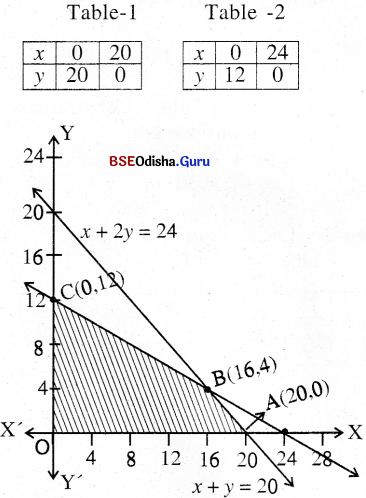
Step – 3 Clearly 0(0,0) satisfies all the constraints.
Thus the shaded region is the feasible region.
From (1) and (2) we get
y = 14
x = 16
With vertices 0(0, 0), A(20, 0), B(16, 4), C(0, 12).
Step – 4 Z(0) = 0
Z(A) = 30,000
Z(B) = 32,000 → Maximum
Z(C) = 24000
Z is maximum for x = 16, y = 4 with Z = 32000
To get maximum profit he must keep 16 sets of model X and 4 sets of model Y.
Maximum profit = 1500 × 16 + 2000 × 4 = ₹32,000
(2) Maximize: 15x + 10y
Subject: x + 3y ≤ 600
2x + y ≤ 480
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
2x +3y = 600
2a + y = 480
Step – 2 Let us draw the graph
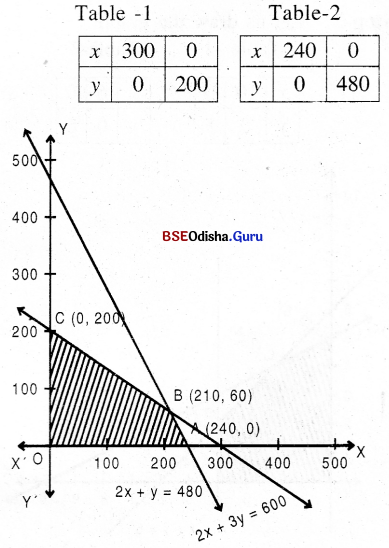
Step – 3 Clearly 0(0,0) satisfies all the constraints.
The corner point are 0(0, 0), A (240, 0) B(210, 60),C(0, 200)
Step – 4 Z(0) = 6
Z(A) = 3600
Z(B) = 3150 + 600
= 3750 → maximum
Z(C) = 2000
Thus Z is maximum for x = 210 and y = 60
and Z(max) = 3750
(3) Maximize: Z = 20x + 30y
Subject to: x + 2y ≤ 10
x + y ≤ 6
x ≤ 4
x, y ≥ 0.
Solution:
Step – 1 Treating the constraints as equations we get
x + 2y = 10 …(1)
x + y = 6 …(2)
x = 4
Step – 2 Let us draw the graph
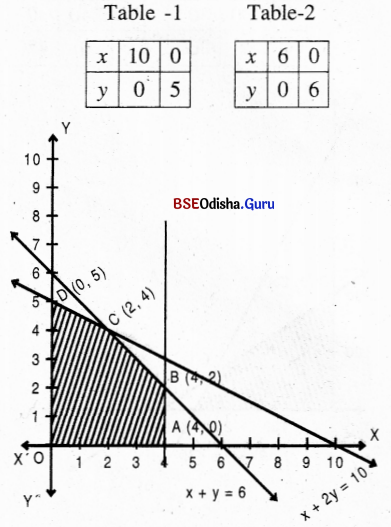
Step – 3 As 0(0,0) satisfies all the constraints the shaded region is the feasible region.
Solving (1) and (2) we get x = 2, y = 4.
The vertices and 0(0, 0) , A(4, 0), B(4, 2), C(2, 4), D (0, 5).
Step – 4 Z(0) =0
Z(A) = 80
Z (B) =140
Z(C) = 1 60 → maximum
Z (D) = 150
∴ Z is Maximum when x = 2, y = 4 and Z(max) = 160
(4) Maximize: Z = 15x + 17y
Subject to: 4x + 7y ≤ 150
x + y ≤ 30
15x + 17y > 300
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
4x + 7y = 150 ….(1)
x + y = 30 ….(2)
15x + 17y = 300 ….(3)
Step – 2 Let us draw the graph
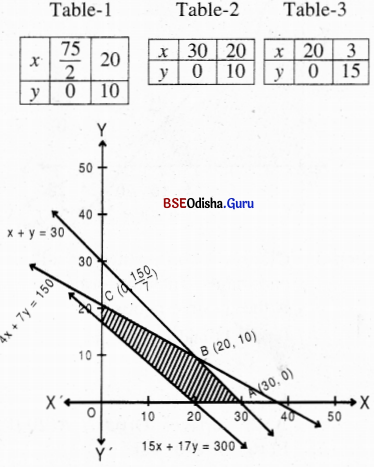
Step – 3 Clearly 0(0,0) satisfies all the constraints.
4x + 7y ≤ 150, x + y ≤ 30, but does not satisfy 15x + 17y ≥ 300.
∴ The shaded region is the feasible region.
From (1) and (2) we get

∴ Z is maximum for x = 20. y = 10 and Z(max) = 470
![]()
(5) Maximize: Z = 2x + 4y
Subject to: 3x + 2y ≤ 10
2x + 5y ≤ 15
5x + 6y ≤ 21
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
3x + 2y = 10 …(1)
2x + 5y = 15 …(2)
5x + 6y = 21 …(3)
Step – 2 Let us draw the graph
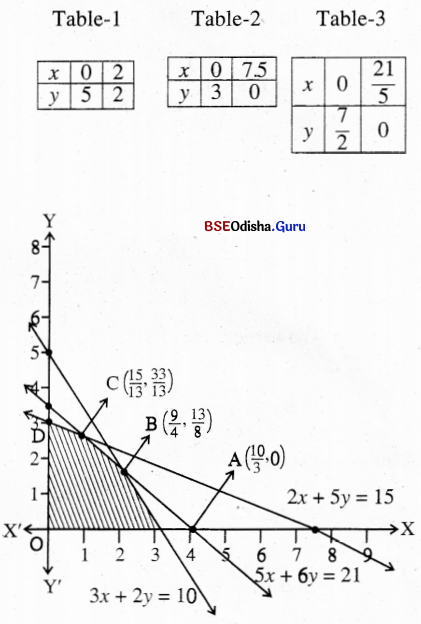
Step – 3 As 0(0,0) satisfies all the constraints the shaded region is the feasible region.
From (1) and (3) we get
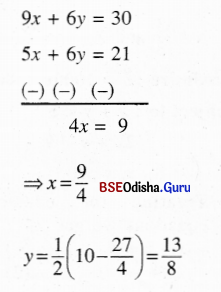
From (2) and (3) we get

Step-4 Z(O) = 0
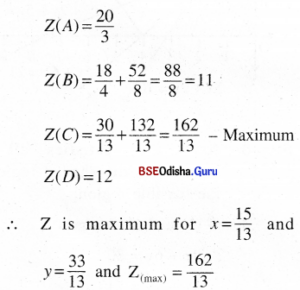
(6) Maximize: Z = 1000x + 800y
Subject to: x + y ≤ 5
2x + y ≤ 9
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x + y = 5 ….(1)
2x + y = 9 ….(2)
Step – 2 Let us draw the graph
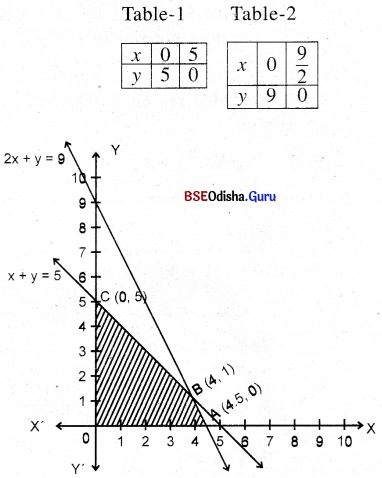
Step – 3 Clearly 0(0,0) satisfies all the constraints.
∴ Thus the shaded region is the feasible region.
From (1) and (2) we get x = 4, y = 1.
∴ The vertices are A(0, 0), A(4.5, 0), B(4, 1) and C(0, 5).
Step – 4 Z(0) =0
Z (A) = 4500
Z (B) = 4800 → Maximum
Z (C) = 4000
Z is maximum for x = 4 and y = 1, Z(max) = 4800
(7) Minimize: Z = 4960 – 70x – 130y
Subject to: x + y ≤ 12
x + y ≥ 6
x ≤ 8
y ≤ 8
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x + y = 12 ….(1)
x + y = 6 ….(2)
x = 8 ….(3)
y = 4 ….(4)
Step – 2 Let us draw the graph
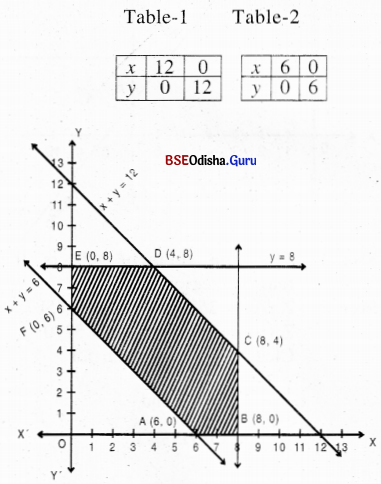
Step – 3 Clearly 0(0,0) satisfies all the constraints except x + y > 6.
The shaded region is the feasible region.
The vertices are A(6, 0), B(8, 0), C(8, 4), D(4, 8), E(0, 8) and F(0, 6).
Step – 4 Z (A) = 4540
Z (B) = 4400
Z (C) = 3880
Z (D) = 3640 → Minimum
Z (E) = 3920
Z (F) = 4180
∴ Z is maximum for x = 4 and y = 8 and Z(min) = 3640.
![]()
(8) Minimize: Z = 16x + 20y
Subject to x + 2y ≥ 10
x + y ≥ 6
3x + y ≥ 8
x, y ≥ 0
Solution:
Step – 1 Treating the constraints as equations we get
x + 2y = 10 ….(1)
x + y = 6 …(2)
3x + y = 8 …(3)
Step – 2 Let us draw the graph
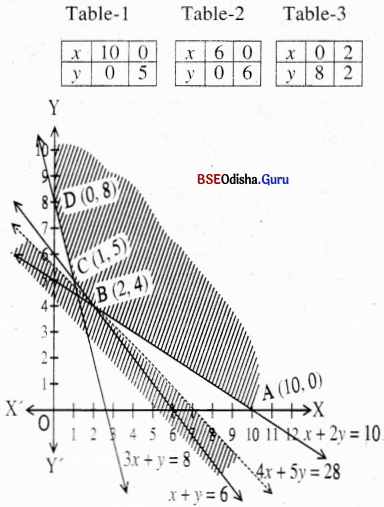
Step – 3 Clearly 0(0,0) satisfies all the constraints. Thus the shaded region is the feasible region.
From (1) and (2) we get y = 4, x = 2.
From (2) and (3) we get x = 1, y = 5.
The vertices are A(10, 0), B(2, 4), C(1, 5), D(0, 8).
Step – 4 Z (A) = 160
Z (B) = 112 → Minimum
Z (C) =116
Z (D) = 160
As the region is unbounded, let us draw the half plane Z < Z(min)
⇒ 16x + 20y < 112
⇒ 4x + 5y < 28
| x1 | 7 | 0 |
| x2 | 0 | 5.6 |
There is no point common to the shaded region and the half plane 4x + 5y ≤ 28 other than B(2, 4).
∴ Z is minimum for x = 2, y = 4 and Z(min) = 112.
(9) Minimize: Z = (512.5)x + 800y
Subject to: 5x + 4y = 40
x ≤ 7
x ≤ 3
x, y ≥ 0
Solution:
Step – 1 Let us draw the graph of
5x + 4y = 40
x = 7, y = 3
| x1 | 8 | 0 |
| x2 | 0 | 10 |
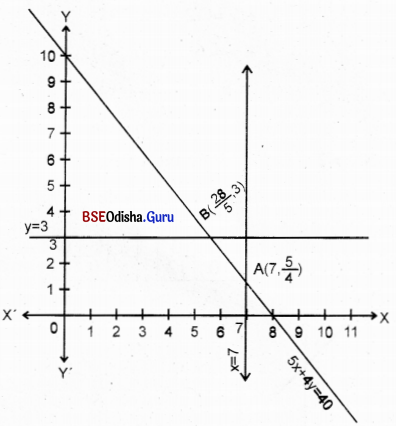
Step – 1 Let us draw the graph of
5x + 4y = 40
x = 7, y = 3
Step – 2 The line segment AB is the feasible region.
Step – 3 Z (A) = 3587.5 + 1000 = 4587.5
Z (B) = 2870 + 2400 = 5270
Clearly Z is minimum for
x = 7, y = \(\frac{5}{4}\) and Z(min) = 4587.5
