CHSE Odisha Class 11 Math Solutions Chapter 4 Trigonometric Functions Ex 4(c)

Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 4 Trigonometric Functions Ex 4(c) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 4 Trigonometric Functions Exercise 4(c)

Question 1.

Fill in the blanks choosing the correct answer from the brackets.

(i) The number of solutions of  2 sin θ – 1 = 0 is__________. (one, two, infinite)
Solution:
Infinite

(ii) If cos α = cos β, then α + β = ____________. (0, π, 2π)
Solution:
2π

(iii) The number of solution(s) of 2 sin θ + 1 = 0 is__________. (zero, two, infinite)
Solution:
Zero

(iv) If tan θ = tan α and 90° < α < 180°, then θ can be in ____________quadrant. (1st, 3rd, 4th)
Solution:
4th

(v) If tan x. tan 2x. tan 7x = tan x + tan 2x + tan 7x, then x = _____________. (\(\frac{\pi}{4}, \frac{\pi}{5}, \frac{\pi}{10}\))
Solution:
\(\frac{\pi}{10}\)

(vi) For_____________value of θ, sin θ + cos θ = √2. (\(\frac{\pi}{4}, \frac{\pi}{2}, \frac{\pi}{3}\))
Solution:
\(\frac{\pi}{4}\)

(vii) The number of values of x for which cos² x = 1 and x² ≤ 4 is______________. (1, 2, 3)
Solution:
1

(viii) In the 1st quadrant the solution of tan² θ = 3 is_____________. (\(\frac{\pi}{2}, \frac{\pi}{3}, \frac{\pi}{4}\))
Solution:
\(\frac{\pi}{3}\)

(ix) The least positive value of θ for which 1 + tan θ = 0 and √2 cos θ + 1 = 0 is___________. (\(\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}\))
Solution:
\(\frac{3 \pi}{4}\)

(x) the least positive value of x for which tan 3x = tan x is______________. (\(\frac{\pi}{2}, \frac{\pi}{3}, \pi\))
Solution:
\(\frac{\pi}{2}\)

Question 2.
Find the principal solution of the following equations:
(i) sin θ = sin 2θ
Solution:
sin θ = sin 2θ
or, 2θ = nπ + (-1)ⁿ θ
or, 2π – (-1)ⁿ θ = nπ
or, θ = \(\frac{n \pi}{2-(-1)^n}\)
when n = 0, θ = 0
when n = 1, θ = \(\frac{\pi}{3}\)
when n = 2, θ = 2π
when n = 3, θ = π
when n = 4, θ = 4π
when n = 5, θ = \(\frac{5 \pi}{3}\)
∴ The principal solution are 0, \(\frac{\pi}{3}\), π, \(\frac{5 \pi}{3}\)

(ii) √3 sin θ – cos θ = 2
Solution:
√3 sin θ – cos θ = 2
or, \(\frac{\sqrt{3}}{2}\) sin θ – 1/2 cos θ = 1

which is the only principal solution.

(iii) cos² θ + sin θ + 1 = 0
Solution:
cos² θ + sin θ + 1 = 0
or, 1 – sin² θ + sin θ + 1 = 0
or,  sin² θ – sin θ + 2 = 0
or, sin² θ – 2 sin θ + sin θ – 2 = 0
or, sinθ(sinθ – 2) + (sinθ – 2) = 0
or, (sinθ – 2) (sinθ + 1) = 0
∴ sinθ = 2, sinθ = – 1
= sin \(\left(-\frac{3 \pi}{2}\right)\) or, θ = – \(\frac{\pi}{2}\), \(\frac{3 \pi}{2}\)
∴ The principal solution is \(\frac{3 \pi}{2}\).

(iv) sin 4x + sin 2x = 0
Solution:

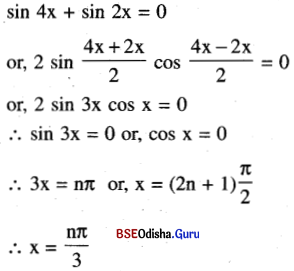
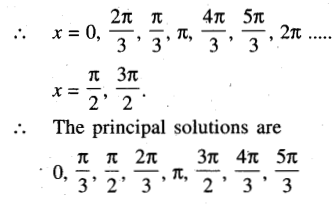
(v) sin x + cos x = \(\frac{1}{\sqrt{2}}\)
Solution:

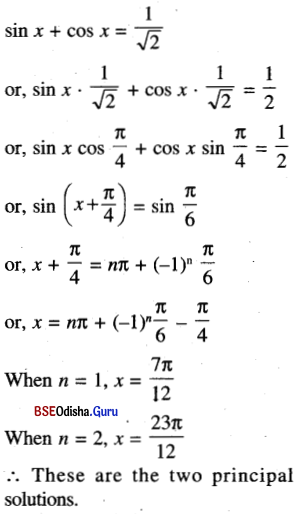
Question 3.
Find the general solution of the following equations:
(i) cos 2x = θ
Solution:
cos 2x = θ
or, 2x = (2n + 1)\(\frac{\pi}{2}\)
or, x = (2n + 1)\(\frac{\pi}{4}\), n∈Z

(ii) sin(x° + 40°) = \(\frac{1}{\sqrt{2}}\)
Solution:

(iii) sin 5θ = sin 3θ
Solution:
sin 5θ = sin 3θ
or, 5θ = nπ + (-1)ⁿ 3θ
or, 5θ – (-1)ⁿ 3θ = nπ
or, θ[5 – (-1)ⁿ3] = nπ
or, θ = \(\frac{n \pi}{5-(-1)^n 3}\)

(iv) tan ax = cot bx
Solution:

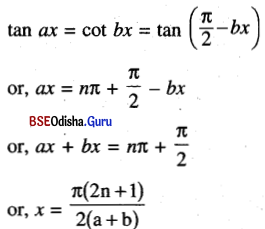
(v) tan² 3θ = 3
Solution:

Question 4.
Solve the following:
(Hints : cos x ≠ 0 and sin² x- sin x + 1/2 = 0)
(i) tan² x + sec² x = 3
Solution:
tan² x + sec² x = 3
or, tan² x + 1 + tan2 x = 3
or, 2tan² x = 2
or, tan² x = 1
or, tan x = ± 1 = tan \(\left(\pm \frac{\pi}{4}\right)\)
∴ x = nπ ± \(\frac{\pi}{4}\)

(ii) 4 sin² x + 6 cos² x = 5
Solution:
4 sin² x + 6 cos² x = 5
or, 4 sin² x + 6(1 – sin² x) = 5
or, 4 sin² x + 6 – 6 sin² x = 5
or, 6- 2 sin² x = 5
or, 2 sin² x = 1
or, sin² x = 1/2
or, sin x = ± \(\frac{1}{\sqrt{2}}\) = sin \(\left(\pm \frac{\pi}{4}\right)\)
or, x = nπ + (-1)ⁿ \(\left(\pm \frac{\pi}{4}\right)\)

(iii) 3 sin x + 4 cos x = 5
Solution:

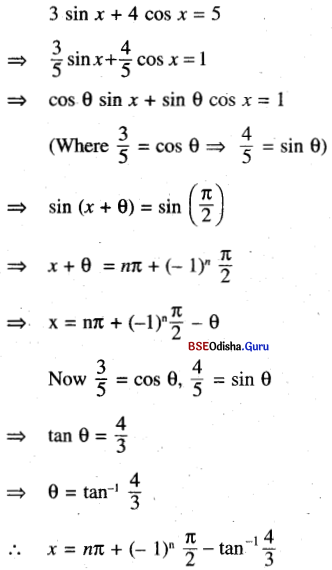
(iv) 3 tan x + cot x = 5 cosec x
Solution:

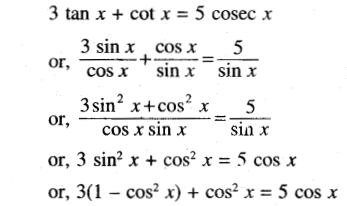
(v) cos x + √3 sin x = √2
Solution:

(vi) sin 3x – 2 cos² x = 0
Solution :
sin 2x – 2 cos² x = 0
or, 2 sin x cos x – 2 cos² x = 0
or, 2 cos x(sin x – cos x) = 0
∴ cos x = 0, sin x = cos x
∴ x = (2n + 1)\(\frac{\pi}{2}\), tan x = 1 = tan \(\frac{\pi}{4}\)
or, x = nπ + \(\frac{\pi}{4}\)

(vii) sec θ + tan θ = √3
Solution:

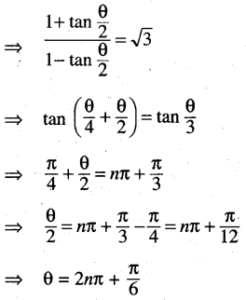
(viii) cos 2θ – cos θ = sin θ – sin 20
Solution:

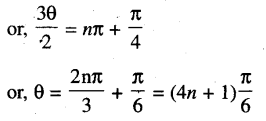
(ix) sin θ + sin 2θ + sin 3θ + sin 4θ = 0
Solution:

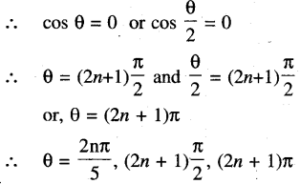
(x) cos 2x° + cos x° – 2 = 0
Solution:
cos 2x° + cos x° – 2 = 0
or, 2 cos² x° – 1 + cos x° – 2 = 0
or, 2 cos² x° + cos x° – 3 = 0
or 2 cos² + 3cos x° – 2cos x°- 3 = 0
or, cos x°(2 cos x° + 3) – 1(2 cos x° + 3) = 0
or, (2 cos x° + 3)(cos x° – 1) = 0
∴ cos x° = 1 = cos 0°
∴ x° = 2nπ ± 0 = 2nπ
or, \(\frac{\pi x}{180}\) = 2nπ
or, x = 360 n
Again 2 cos x° + 3 = 0
⇒ cos x° = – 3/2 which has no solution.
Hence x = 360 n.

(xi) tan θ + tan 2θ = tan 3θ
Solution:

(xii) tan θ + tan (\(\theta+\frac{\pi}{3}\)) + tan (\(\theta+\frac{2\pi}{3}\)) = 3
Solution:

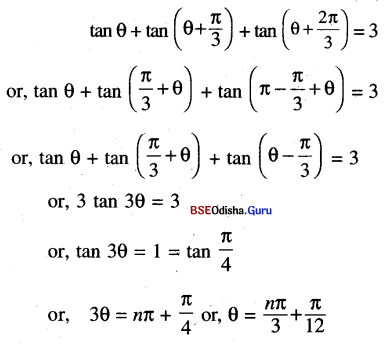
(xiii) cot² θ – tan² θ = 4 cot 2θ
Solution:

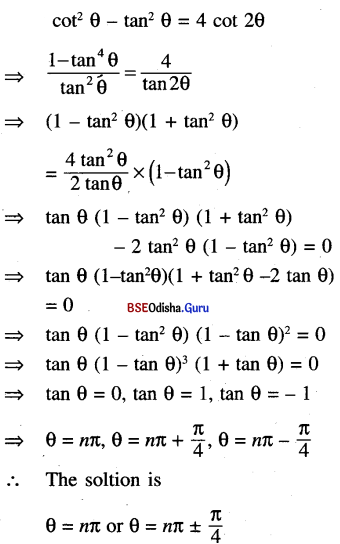
(xiv) cos 2θ = \((\sqrt{2}+1)\left(\cos \theta-\frac{1}{\sqrt{2}}\right)\)
Solution:

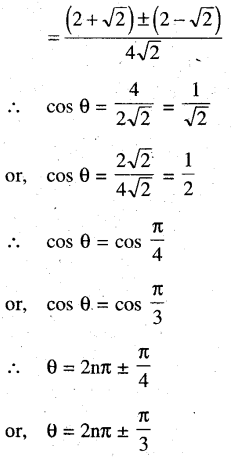
(xv) sec θ – 1 = \((\sqrt{2}-1)\) tan θ
Solution:

⇒ θ = 2nπ + \(\frac{\pi}{4}\)

(xvi) 3cot² θ – 2 sin θ = 0
Solution:

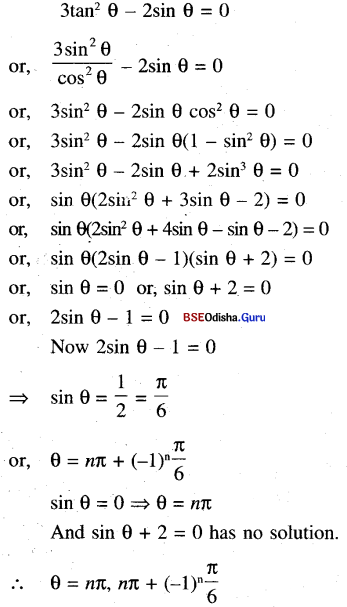
(xvii) 4 cos x. cos 2x . cos 3x = 1
Solution:
4 cos x cos 2x cos 3x = 1
⇒ 2 cos x cos 2x. 2 cos 3x = 1
⇒ (cos 3x + cos x) 2 cos 3x = 1
⇒ 2 cos² 3x + 2 cos 3x cos x = 1
⇒ 2 cos² 3x – 1 + cos 4x + cos 2x = 0
⇒ cos 6x + cos 4x + cos 2x = 0
⇒ cos 6x + cos 2x + cos 4x = 0
⇒ 2 cos 4x cos 2x + cos 4x = 0
⇒ cos 4x (2 cos 2x + 1) = 0
⇒ cos 4x = 0, cos 2x = – 1/2
cos 4x = 0 ⇒ 4x = (2n + 1) \(\frac{\pi}{2}\)

(xviii) cos 3x – cos 2x = sin 3x
Solution:

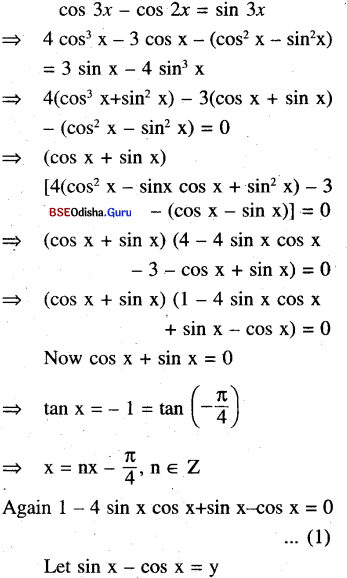
⇒ 1 – 2 sin x cos x = y²
∴ Equation (1) reduces to
1 – 2(1 – y²) + y = 0
⇒ 2y² + y – 1 = 0
⇒ (2y- 1) (y + 1) = 0

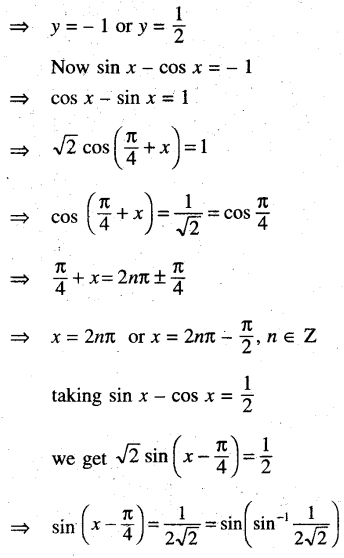
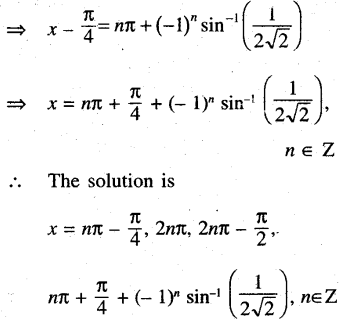
(xix) cos x + sin x = cos 2x + sin 2x
Solution:
cos x + sin x – cos 2x + sin 2x
[Refer (viii)]

(xx) tan x + tan 4x + tan 7x = tan x. tan 4x. tan 7x
Solution:
tan x + tan 4x + tan 7x = tan x tan 4x tan 7x
or, tan x + tan 4x
= – tan 7x + tan x tan 4x tan 7x
= – tan 7x (1 – tan x tan 4x)
or, \(\frac{\tan x+\tan 4 x}{1-\tan x \tan 4 x}\) = – tan 7x
or, tan (x + 4x) = tan (π – 7x)
or, tan 5x = tan (π – 7x)
or, 5x = nπ + π – 7x
or, 12x = π(n + 1)
or, x = \(\frac{\pi(n+1)}{12}\), n∈Z

(xxi) 2(sec² θ + sin² θ) = 5
Solution:

(xxii) \((\cos x)^{\sin ^2 x-\frac{3}{2} \sin x+\frac{1}{2}}=1\)
Solution:
\((\cos x)^{\sin ^2 x-\frac{3}{2} \sin x+\frac{1}{2}}=0\)
As cos x ≠ 0.
we have sin² – \(\frac{3}{2}\) sin x + \(\frac{1}{2}\) = 0
∴ 2 sin² x – 3 sin x + 1 = 0
or, 2 sin² x – 2 sin x – sin x + 1 = 0
or, (2sin x – 1)(sin x – 1) = 0
∴ sin x = \(\frac{1}{2}\) or, sin x = 1
But as cos x ≠ 0, we have sin x ≠ 1
∴ sin x = \(\frac{1}{2}\) = sin \(\frac{\pi}{6}\)
∴ x = nπ + (-1)ⁿ \(\frac{\pi}{6}\), n∈Z