Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Additional Exercise Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 3 Linear Programming Additional Exercise
(A) Multiple Choice Questions (Mcqs) With Answers
Question 1.
Write the value of cos-1 cos(3π/2).
(a) π
(b) \(\frac{\pi}{2}\)
(c) \(\frac{\pi}{4}\)
(d) 2π
Solution:
(b) \(\frac{\pi}{2}\)
Question 2.
Sets A and B have respectively m and n elements. The total number of relations from A to B is 64. If m < n and m ≠ 1, write the values of m and n respectively.
(a) m = 3, n = 2
(b) m = 2, n = 2
(c) m = 2, n = 3
(d) m = 3, n = 3
Solution:
(c) m = 2, n = 3
Question 3.
Write the principal value of
sin-1 (\(-\frac{1}{2}\)) + cos-1 cos(\( -\frac{\pi}{2}\))
(a) \(\frac{\pi}{2}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{4}\)
(d) π
Solution:
(b) \(\frac{\pi}{3}\)
Question 4.
Write the maximum value of x + y subject to: 2x + 3y < 6, x > 0, y > 0.
(a) 3
(b) 1
(c) 2
(d) 0
Solution:
(a) 3
![]()
Question 5.
Let A has 3 elements and B has m elements. Number of relations from A to B = 4096. Find the value of m.
(a) 2
(b) 4
(c) 1
(d) 3
Solution:
(b) 4
Question 6.
Let A is any non-empty set. Number of binary operations on A is 16. Find |A|.
(a) 2
(b) 1
(c) 3
(d) 4
Solution:
(a) 2
Question 7.
Give an example of a relation which is reflexive, transitive but not symmetric.
(a) x < y on Z
(b) x = y on Z
(c) x > y on Z
(d) None of the above
Solution:
(a) x < y on Z
Question 8.
Find the least positive integer r such that – 375 ∈ [r]11
(a) r = 5
(b) r = 6
(c) r = 3
(d) r = 10
Solution:
(d) r = 10
Question 9.
Find three positive integers xi, i = 1, 2, 3 satisfying 3x ≡ 2 (mod 7)
(a) x = 1, 3, 9…
(b) x = 2, 4, 6…
(c) x = 3, 10, 17…
(d) x = 2, 10, 18…
Solution:
(c) x = 3, 10, 17…
Question 10.
If the inversible function f is defined as f(x) = \(\frac{3 x-4}{5}\) write f-1(x)
(a) \(\frac{5 x+4}{3}\)
(b) \(\frac{4 x+5}{3}\)
(c) \(\frac{5 x-4}{3}\)
(d) \(\frac{5 x+4}{2}\)
Solution:
(a) \(\frac{5 x+4}{3}\)
Question 11.
Let f : R → R and g : R → R defined as f(x) = |x|, g(x) = |5x – 2| then find fog.
(a) |5x + 2|
(b) |5x – 2|
(c) |2x – 2|
(d) |2x – 5|
Solution:
(b) |5x – 2|
Question 12.
Let ∗ is a binary operation defined by a ∗ b = 3a + 4b – 2, find 4 ∗ 5.
(a) 20
(b) 12
(c) 30
(d) 36
Solution:
(c) 30
![]()
Question 13.
Let the binary operation on Q defined as a ∗ b = 2a + b – ab, find 3 ∗ 4.
(a) -2
(b) -1
(c) 2
(d) 1
Solution:
(a) -2
Question 14.
Let ∗ is a binary operation on Z defined as a ∗ b = a + b – 5 find the identity element for ∗ on Z.
(a) e = 1
(b) e = 5
(c) e = -5
(d) e = -1
Solution:
(b) e = 5
Question 15.
Find the number of binary, operations on the set {a, b}.
(a) 12
(b) 14
(c) 15
(d) 16
Solution:
(d) 16
Question 16.
Let ∗ is a binary operation on [0, ¥) defined as a ∗ b = \(\sqrt{a^2+b^2}\) find the identity element.
(a) e = 0
(b) e = 2
(c) e = 1
(d) e = 3
Solution:
(a) e = 0
Question 17.
Find least non-negative integer r such that 7 × 13 × 23 × 413 ≡ r (mod 11).
(a) r = 13
(b) r = 49
(c) r = 7
(d) r = 23
Solution:
(c) r = 7
Question 18.
Find least non-negative integer r such that 1237(mod 4) + 985 (mod 4) ≡ r (mod 4).
(a) r = 1
(b) r = 2
(c) r = -2
(d) r = -1
Solution:
(b) r = 2
Question 19.
Let ∗ is a binary operation on R – {0} defined as a ∗ b = \(\frac{a b}{5}\). If 2 ∗ (x ∗ 5) = 10, then find x:
(a) x = 25
(b) x = -5
(c) x = 5
(d) x = 1
Solution:
(a) x = 25
![]()
Question 20.
Find the principal value of cos-1 (\( -\frac{1}{2}\)) + 2sin-1 (\( \frac{1}{2}\)).
(a) \(\frac{5 \pi}{6}\)
(b) \(\frac{5 \pi}{2}\)
(c) \(\frac{5 \pi}{4}\)
(d) \(\frac{\pi}{6}\)
Solution:
(a) \(\frac{5 \pi}{6}\)
Question 21.
Evaluate sin-1 (\(\frac{1}{\sqrt{5}}\)) + cos-1 (\(\frac{3}{\sqrt{10}}\))
(a) \(\frac{\pi}{2}\)
(b) \(\frac{\pi}{5}\)
(c) \(\frac{\pi}{4}\)
(d) π
Solution:
(c) \(\frac{\pi}{4}\)
Question 22.
Evaluate cos-1 (\(\frac{1}{2}\)) + 2sin-1 (\(\frac{1}{2}\)).
(a) \(\frac{2 \pi}{5}\)
(b) \(\frac{2 \pi}{3}\)
(c) π
(d) \(\frac{\pi}{3}\)
Solution:
(b) \(\frac{2 \pi}{3}\)
Question 23.
Find the value of tan-1 √3 – sec-1 (-2).
(a) –\(\frac{\pi}{3}\)
(b) \(\frac{2 \pi}{3}\)
(c) \(\frac{\pi}{3}\)
(d) \(\frac{3 \pi}{2}\)
Solution:
(a) –\(\frac{\pi}{3}\)
Question 24.
Evaluate tan (2 tan-1 \(\frac{1}{3}\))
(a) 2
(b) 1
(c) 0
(d) -1
Solution:
(a) 2
Question 25.
Evaluate : sin-1 (sin \(\frac{3 \pi}{5}\)).
(a) \(-\frac{2 \pi}{3}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{2 \pi}{5}\)
(d) \(\frac{\pi}{5}\)
Solution:
(c) \(\frac{2 \pi}{5}\)
![]()
Question 26.
tan-1 (2cos\(\frac{\pi}{3}\)) is ________.
(a) \(\frac{\pi}{2}\)
(b) \(\frac{\pi}{4}\)
(c) \(\frac{\pi}{5}\)
(d) \(\frac{\pi}{3}\)
Solution:
(b) \(\frac{\pi}{4}\)
Question 27.
Evaluate : sin-1 (sin \(\frac{2 \pi}{3}\)) is ________.
(a) \(\frac{\pi}{2}\)
(b) \(\frac{\pi}{4}\)
(c) \(\frac{\pi}{5}\)
(d) \(\frac{\pi}{3}\)
Solution:
(d) \(\frac{\pi}{3}\)
Question 28.
The value of sin(tan-1 x + tan-1 \( \frac{1}{x}\)), x > 0 = ________.
(a) -1
(b) 1
(c) 0
(d) 2
Solution:
(b) 1
Question 29.
2sin-1 \( \frac{4}{5}\) + sin-1 \( \frac{24}{25}\) = ________.
(a) 12
(b) 15
(c) 16
(d) 20
Solution:
(b) 15
Question 30.
Evaluate: tan-1 1 = (2cos\(\frac{\pi}{3}\))
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{2}\)
(c) \(\frac{\pi}{3}\)
(d) \(\frac{2 \pi}{3}\)
Solution:
(a) \(\frac{\pi}{4}\)
Question 31.
If sin-1 (\( \frac{\pi}{5}\)) + cosec-1 (\(\frac{5}{4}\)) = \(\frac{5}{2}\) then find the value of x.
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3
Question 32.
Evaluate:
tan-1 (\( \frac{-1}{\sqrt{3}}\)) + cot-1 (\( \frac{1}{\sqrt{3}}\)) + tan-1(sin(\( -\frac{\pi}{2}\))).
(a) \(\frac{- \pi}{12}\)
(b) \(\frac{2 \pi}{5}\)
(c) \(\frac{\pi}{12}\)
(d) \(\frac{\pi}{6}\)
Solution:
(a) \(\frac{- \pi}{12}\)
Question 33.
Evaluate sin-1 (cos(\( \frac{33 \pi}{5}\)))
(a) \(\frac{\pi}{10}\)
(b) \(\frac{- \pi}{10}\)
(c) \(\frac{\pi}{5}\)
(d) \(\frac{\pi}{2}\)
Solution:
(b) \(\frac{- \pi}{10}\)
Question 34.
Express the value of the following in simplest form. tan (\( \frac{\pi}{4}\) + 2cot-1 3)
(a) 7
(b) 12
(c) 3
(d) 6
Solution:
(a) 7
![]()
Question 35.
Express the value of the following in simplest form sin cos-1 tan sec-1 √2
(a) cos 0
(b) cot 0
(c) tan 0
(d) sin 0
Solution:
(d) sin 0
Question 36.
tan \(\left\{\frac{1}{2} \sin ^{-1} \frac{2 x}{1+x^2}+\frac{1}{2} \cos ^{-1} \frac{1-y^2}{1+y^2}\right\}\)
(a) \(\frac{x-y}{1+x y}\)
(b) \(\frac{x+y}{1-x y}\)
(c) \(\frac{x-y}{1+y}\)
(d) \(\frac{x+y}{x y}\)
Solution:
(b) \(\frac{x+y}{1-x y}\)
Question 37.
The relation R on the set A = [1, 2, 3] given by R = {(1, 1), (1, 2), (2, 2), (2, 3), (3, 3)} is:
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Equivalence
Solution:
(a) Reflexive
Question 38.
Let f : R → R be defined as f(x) = 3x – 2. Choose the correct answer.
(a) f is one-one onto
(b) f is many-one onto
(c) f is one-one but not onto
(d) f is neither one-one nor onto
Solution:
(a) f is one-one onto
Question 39.
Let R be a relation defined on Z as R = {(a, b) ; a2 + b2 = 25 }, the domain of R is:
(a) {3, 4, 5}
(b) {0, 3, 4, 5}
(c) {0, 3, 4, 5, -3, -4, -5}
(d) None of the above
Solution:
(c) {0, 3, 4, 5, -3, -4, -5}
Question 40.
let R be the relation in the set N given by R={(a, b) : a = b – 2, b > 6}. Choose the correct answer.
(a) (2, 4) • R
(b) (3, 8) • R
(c) (6, 8) • R
(d) (8, 10) • R
Solution:
(d) (8, 10) • R
Question 41.
Set A has 3 elements and set B has 4 elements. Then the number of injective functions that can be defined from set A to set B is
(a) 144
(b) 12
(c) 24
(d) 64
Solution:
(c) 24
Question 42.
Let R be a relation on set of lines as L1 R L2 if L1 is perpendicular to L2. Then
(a) R is Reflexive
(b) R is transitive
(c) R is symmetric
(d) R is an equivalence relation
Solution:
(c) R is symmetric
Question 43.
A Relation from A to B is an arbitrary subset of:
(a) A × B
(b) B × B
(c) A × A
(d) B × B
Solution:
(a) A × B
Question 44.
Let T be the set of all triangles in the Euclidean plane, and let a relation R on T be defined as aRb if a is congruent to b ∀ a, b ∈ T. Then R is
(a) reflexive but not transitive
(b) transitive but not symmetric
(c) equivalence
(d) None of these
Solution:
(c) equivalence
![]()
Question 45.
The maximum number of equivalence relations on the set A = {1, 2, 3} are
(a) 1
(b) 2
(c) 3
(d) 5
Solution:
(d) 5
Question 46.
Let A = {1, 2, 3} and consider the relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}. Then R is
(a) reflexive but not symmetric
(b) reflexive but not transitive
(c) symmetric and transitive
(d) neither symmetric nor transitive
Solution:
(a) reflexive but not symmetric
Question 47.
Which of the following functions from Z into Z are bijective?
f(x) = x3
f(x) = x + 2
f(x) = 2x + 1
f(x) = x2 + 1
Solution:
f(x) = x + 2
Question 48.
Let R be a relation on the set N of natural numbers denoted by nRm <=> n is a factor of m (i.e. n | m). Then, R is
(a) Reflexive and symmetric
(b) Transitive and symmetric
(c) Equivalence
(d) Reflexive, transitive but not symmetric
Solution:
(c) Equivalence
Question 49.
Let S = {1, 2, 3, 4, 5} and let A = S × S. Define the relation R on A as follows: (a, b) R (c, d) iff ad = cb. Then, R is
(a) reflexive only
(b) Symmetric only
(c) Transitive only
(d) Equivalence relation
Solution:
(d) Equivalence relation
Question 50.
Let X = {-1, 0, 1}, Y = {0, 2} and a function f : X → Y defined by y = 2x4, is
(a) one-one onto
(b) one-one into
(c) many-one onto
(d)many-one into
Solution:
(c) many-one onto
Question 51.
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by f(x) = (x-2)/(x-3). Then,
(a) f is bijective
(b) f is one-one but not onto
(c) f is onto but not one-one
(d) None of these
Solution:
(a) f is bijective
Question 52.
The function f : R → R given by f(x) = x3 – 1 is
(a) a one-one function
(b) an onto function
(c) a bijection
(d) neither one-one nor onto
Solution:
(c) a bijection
Question 53.
Let f : [0, ∞) → [0, 2] be defined by f(x) = 2x/1+x, then f is
(a) one-one but not onto
(b) onto but not one-one
(c) both one-one and onto
(d) neither one-one nor onto
Solution:
(a) one-one but not onto
Question 54.
If N be the set of all natural numbers, consider f : N → N such that f(x) = 2x, ∀ × ∈ N, then f is
(a) one-one onto
(b) one-one into
(c) many-one onto
(d) None of these
Solution:
(b) one-one into
![]()
Question 55.
Let f : R → R be a function defined by f(x) = x3 + 4, then f is
(a) injective
(b) surjective
(c) bijective
(d) none of these
Solution:
(c) bijective
Question 56.
Given set A = {a, b, c}. An identity relation in set A is
(a) R = {(a, b), (a, c)}
(b) R = {(a, a), (b, b), (c, c)}
(c) R = {(a, a), (b, b), (c, c), (a, c)}
(d) R= {(c, a), (b, a), (a, a)}
Solution:
(b) R = {(a, a), (b, b), (c, c)}
Question 57.
Set A has 3 elements and the set B has 4 elements. Then the number of injective functions that can be defined from set A to set B is
(a) 144
(b) 12
(c) 24
(d) 64
Solution:
(c) 24
Question 58.
sin(sec-1 x + cosec-1 x) =
(a) 1
(b) -1
(c) π/2
(d) π/3
Solution:
(a) 1
Question 59.
The principle value of sin-1 (√3/2) is:
(a) 2π/3
(b) π/6
(C) π/4
(d) π/3
Solution:
(d) π/3
Question 60.
Simplified form of cos-1 (4x3 – 3x)
(a) 3 sin-1 x
(b) 3 cos-1 x
(c) π – 3 sin-1 x
(d) None of these
Solution:
(b) 3 cos-1 x
Question 61.
tan-1 √3 – sec-1 (-2) is equal to
(a) π
(b) -π/3
(c) π/3,
(d) 2π/3
Solution:
(b) -π/3
Question 62.
If y = sec-1 x then
(a) 0 ≤ y ≤ π
(b) 0 ≤ y ≤ π/2
(c) -π/2 ≤ y ≤ π/2
(d) None of these
Solution:
(d) None of these
![]()
Question 63.
If x + (1/x) = 2 then the principal value of sin-1 x is
(a) π/4
(b) π/2
(c) π
(d) 3π/2
Solution:
(b) π/2
Question 64.
The principle value of sin-1 (sin 2π/3) is :
(a) 2π/3
(b) π/3
(c) -π/6
(d) π/6
Solution:
(b) π/3
Question 65.
The value of cos-1 (1/2) + 2sin-1 (1/2) is equal to
(a) π/4
(b) π/6
(c) 2π/3
(d) 5π/6
Solution:
(b) π/6
Question 66.
Principal value of tan-1 (-1) is
(a) π/4
(b) -π/2
(c) 5π/4
(d) -π/4
Solution:
(d) -π/4
Question 67.
A Linear function, which is minimized or maximized is called
(a) an objective function
(b) an optimal function
(c) A feasible function
(d) None of these
Solution:
(a) an objective function
Question 68.
The maximum value of Z = 3x + 4y subject to the constraints : x+ y ≤ 4, x ≥ 0, y ≥ 0 is:
(a) 0
(b) 12
(c) 16
(d) 18
Solution:
(c) 16
Question 69.
The maximum value of Z = 2x +3y subject to the constraints : x + y ≤ 1, 3x + y ≤ 4, x, y ≥ 0 is
(a) 2
(b) 4
(c) 5
(d) 3
Solution:
(c) 5
Question 70.
The point in the half plane 2x + 3y – 12 ≥ 0 is:
(a) (-7,8)
(c) (-7,-8)
(b) (7, -8)
(d) (7, 8)
Solution:
(d) (7, 8)
Question 71.
Any feasible solution which maximizes or minimizes the objective function is Called:
(a) A regional feasible solution
(b) An optimal feasible solution
(c) An objective feasible solution
(d) None of these
Solution:
(b) An optimal feasible solution
Question 72.
Objective function of a LPP is
(a) a constraint
(b) a function to be optimized
(c) a relation between the variables
(d) none of these
Solution:
(b) a function to be optimized
![]()
(B) Very Short Type Questions With Answers
Question 1.
If R is a relation on A such that R = R-1, then write the type of the relation R.
Solution:
We know that (a, b) ∈ R ⇒ (b, a) ∈ R-1
As R = R-1, so R is symmetric. [2019(A)
Question 2.
Write the value of cos-1 cos (\(\frac{3 \pi}{2}\)). [2019(A)
Solution:
cos-1 cos (\(\frac{3 \pi}{2}\)) = cos-1 (0) = \(\frac{\pi}{2}\)
Question 3.
Sets A and B have respectively m and n elements. The total number of relations from A to B is 64. If m < n and m ≠ 1, write the values of m and n respectively. [2018(A)
Solution:
|A| = m and |B| = n
Number of relations from A to B = 2mn.
A.T.Q. 2mn = 64 = 26.
⇒ mn = 6, m < n with m ≠ 1.
∴m = 2, n = 3
Question 4.
Write the principal value of sin-1 (\(\frac{- 1}{2}\)) + cos-1 cos(\(\frac{- \pi}{2}\)) [2018(A)
Solution:
sin-1 (\(\frac{- 1}{2}\)) + cos-1 (cos\(\frac{- \pi}{2}\)) = \(\frac{- \pi}{6}\) + \(\frac{\pi}{2}\) = \(-\frac{\pi}{3}\)
Question 5.
Write the maximum value of x + y subject to: 2x + 3y ≤ 6, x ≥ 0, y ≥ 0. [2011(A)
Solution:
2x + 3y = 6 intersects the axes at (3, 0) and (0, 2)
∴ The maximum value of x + y = 3.
Question 6.
Define ‘feasible’ solution of an LPP. [2009(A)
Solution:
The solutions of LPP which satisfy all the constraints and non-negative restrictions are called feasible solutions.
Question 7.
Mention the quadrant in which the solution of an LPP with two decision variables lies when the graphical method is adopted. [2008(A)
Solution:
The solution lies in XOY or 1st quadrant.
Question 8.
Write the smallest equivalence relation on A = {1, 2, 3}.
Solution:
The relation R = {(1, 1), (2, 2), (3, 3)} is the smallest equivalence relation on set A.
Question 9.
Congruence modulo 3 relation partitions the set Z into how many equivalence classes?
Solution:
The relation congruence modulo 3 on the set Z partitions Z into three equivalence classes.
Question 10.
Give an example of a relation which is reflexive, symmetric but not transitive.
Solution:
The relation R = {(a, b), (b, a), (a, c), (c, a), (a, a), (b, b), (c, c)} defined on the set {a, b, c} is reflexive, symmetric but not transitive.
![]()
Question 11.
Give an example of a relation which is reflexive, transitive but not symmetric.
Solution:
‘‘The relation x ≤ y on Z” is reflexive, transitive but not symmetric.
Question 12.
Give an example of a relation which is reflexive but neither symmetric nor transitive.
Solution:
The relation R = {(a, a), (b, b), (c, c), (a, b), (b, c)} defined on the set A = {a, b, c} is reflexive but neither symmetric nor transitive.
Question 13.
Find three positive integers xi, i =1, 2, 3 satisfying 3x ≡ 2 (mod 7)
Solution:
3x ≡ 2 mod 7
Least positive value of x = 3
Each member of [3] is a solution
∴ x = 3, 10, 17…
Question 14.
State the reason for relation R on {1, 2, 3} defined as {(1, 2), (2, 1)} is not transitive.
Solution:
(1, 2), (2, 1) ∈ R but (1, 1) ∉ R
∴ R is not transitive.
Question 15.
Give an example of a function which is injective but not surjective.
Solution:
f(x) = \(\frac{x}{2}\) from Z → R is injective but not surjective.
Question 16.
Let X = {1, 2, 3, 4}. Determine whether
f : X → X defined as given below have inverses. Find f-1 if it exists:
f = {(1, 2), (2, 2), (3, 2), (4, 2)}
Solution:
f is not injective hence not invertible.
Question 17.
Let ∗ is a binary operation defined by a ∗ b = 3a + 4b – 2, find 4 ∗ 5.
Solution:
4 ∗ 5 = 3 × 4 + 4 × 5 – 2
= 12 + 20 – 2
= 30
Question 18.
Let the binary operation on Q defined as a ∗ b = 2a + b – ab, find 3 ∗ 4.
Solution:
3 ∗ 4 = 6 + 4 – 12 = -2
Question 19.
Let ∗ is a binary operation on Z defined as a ∗ b = a + b – 5 find the identity element for ∗ on Z.
Solution:
Let e is the identity element.
⇒ a ∗ e = e ∗ a = a
⇒ a + e – 5 = a
⇒ e = 5
Question 20.
Find the number of binary operations on the set {a, b}.
Solution:
Number of binary operations on
{a, b} = 222 = e4 =16.
![]()
Question 21.
Let * is a binary operation on [0, ¥) defined as a * b = \(\sqrt{\mathbf{a}^2+\mathbf{b}^2}\) find the identity element.
Solution:
Let e is the identity element
⇒ a * e = \(\sqrt{\mathbf{a}^2+\mathbf{e}^2}\) = a
⇒ a2 + e2 = a2
⇒ e = 0
Question 22.
Evaluate cos-1 (\(\frac{1}{2}\)) + 2 sin-1 (\(\frac{1}{2}\)).
Solution:
cos-1 (\(\frac{1}{2}\)) + 2 sin-1 (\(\frac{1}{2}\))
= \(\frac{\pi}{3}\) + 2 × \(\frac{\pi}{6}\) = \(\frac{2 \pi}{3}\)
Question 23.
Find the value of tan-1 √3 – sec-1 (-2)
Solution:
tan-1 √3 – sec-1 (-2)
= \(\frac{\pi}{3}\) – \(\frac{2 \pi}{3}\) = – \(\frac{\pi}{3}\).
Question 24.
Evaluate tan (2 tan-1 \(\frac{1}{3}\))
Solution:
tan (2 tan-1 \(\frac{1}{3}\)) = tan tan-1 \(\left(\frac{\frac{2}{3}}{1-\frac{2}{3}}\right)\)
= tan tan-1 (2) = 2
Question 25.
Evaluate: sin-1 (sin \(\frac{3 \pi}{5}\)).
Solution:
sin-1 (sin \(\frac{3 \pi}{5}\)) = sin-1 sin (\(\pi \frac{-2 \pi}{5}\))
= sin-1 sin \(\frac{2 \pi}{5}\) = \(\frac{2 \pi}{5}\)
Question 26.
Evaluate tan-1 1 = (2 cos \(\frac{\pi}{3}\))
Solution:
tan-1 (2 cos \(\frac{\pi}{3}\))
= tan-1 (2 × 1/2) = tan-1 1 = \(\frac{\pi}{4}\)
Question 27.
Define the objective function.
Solution:
If C1, C2, C3 …. Cn are constants and x1, x2, …… xn are variables then the linear function z = C1x1 + C2x2 +…… Cnxn which is to be optimized is called an objective function.
Question 28.
Define feasible solution.
Solution:
A set of values of the variables x1, x2, …… xn is called a feasible solution of LPP if it satisfies the constraints and non-negative restrictions of the problem.
Question 29.
Define a convex set.
Solution:
A set is convex if every point on the line segment joining any two points lies on it.
Question 30.
State extreme point theorem.
Solution:
Let S is a convex polygon bounded by the straight lines. The linear function z = Ax + By attains its optimum value at the vertices of S.
![]()
(C) Short Type Questions With Answers
Question 1.
Construct the multiplication table X7 on the set {1, 2, 3, 4, 5, 6}. Also find the inverse element of 4 if it exists. [2019(A)
Solution:
Given set A = { 1, 2, 3, 4, 5, 6} Binary operation ∗ defined on A is X7.
i.e. a ∗ b = a × b mod 7
= The remainder on dividing a × b by 7
The composition table for this operation is:
| ∗ | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 |
As the second row is identical to first row, we have ‘1’ as the identity element.
As 4 ∗ 2 = 2 ∗ 4 = 1 we have 4-1 = 2
Question 2.
Let R be a relation on the set R of real numbers such that aRb iff a – b is an integer. Test whether R is an equivalence relation. If so, find the equivalence class of 1 and \(\frac{1}{2}\). [2019(A)
Solution:
The relation R on the set of real numbers is defined as
R = { (a, b) : a – b ∈ Z}
Reflexive:
∀ a ∈ R (set of real numbers)
a – a = 0 ∈ Z
⇒ (a, a) ∈ R
⇒ R is reflexive
Symmetric:
Let (a, b) ∈ R
⇒ a – b ∈ Z
⇒ b – a ∈ Z
⇒ (b, a) ∈ R
⇒ R is symmetric.
Transitive:
Let (a, b), (b, c) ∈ R
⇒ a – b and b – c ∈ Z
⇒ a – b + b – c ∈ Z
⇒ a – c ∈ Z
⇒ (a, c) ∈ R
⇒ R is transitive
Thus R is an equivalence relation
[1] = { x ∈ R : x – 1 ∈ Z} = Z
\(\frac{1}{2}\) = { x ∈ R : x – \(\frac{1}{2}\) ∈ Z}
= {x ∈ R : x = \(\frac{2 k+1}{2}\), k ∈ Z}
Question 3.
Two types of food X and Y are mixed to prepare a mixture in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. These vitamins are available in 1 kg of food as per the table given below: [2019(A)
| Vitamin | |||
| Food | A | B | C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
1 kg of food X costs ₹16 and 1 kg of food Y costs ₹20. Formulate the LPP so as to determine the least cost of the mixture containing the required amount of vitamins.
Solution:
Let x kg of food X and Y kg of food y are to be mixed to prepare the mixture.
Total cost = 16x + 20y to be minimum.
According to the question
Total vitamin A = x + 2y ≥ 10 units
Total vitamin B = 2x + 2y ≥ 12 units
Total vitamin C = 3x + y ≥ 8 units.
∴ The required LPP is minimize
Z= 16x + 20y
Subject to : x + 2y ≥ 10
x + y ≥ 6
3x + y ≥ 8
x, y ≥ 0
Question 4.
Let ~ be defined by (m, n) ~ (p, q) if mq = np, where m, n, p, q e Z – {0}. Show that it is an equivalence relation. [2018(A)
Solution:
Let A = z – {0}
~ is a relation on A x A defined as (m, n) ~ (p, q) ⇔ mq = np
Reflexive : For all (m, n) ∈ A × A
We have mn = nm
⇒ (m, n) ~ (m, n)
∴ ~ is reflexive.
Symmetric: Let {m, n), (p, q) ∈ A × A and (m, n) ~ (p, q)
⇒ mq = np
⇒ pn = qm
(p, q) ~ (m, n)
∴ ~ is symmetric.
Transitive: Let (m, n), (p, q), (x, y) ∈ A × A
and (m, n) ~ (p, q), (p, q) ~ (x, y)
⇒ mq = np and py = qx
⇒ mqpy = npqx
⇒ my = nx
⇒ (m, n) ~ (x, y)
∴ ~ is transitive.
Thus ~ is an equivalence relation.
![]()
Question 5.
Solve the following LPP graphically:
Minimize Z = 4x + 3y
subject to 2x + 5y ≥ 10
x, y ≥ 0. [2018(A)
Solution:
Given LPP is:
Minimize: Z = 4x + 3y
Subject to: 2x + 5y ≥ 10
x, y ≥ 0
Step – 1 Considering the constraints as equations we have 2x + 5y = 10
| x | 5 | 0 |
| y | 0 | 2 |
Let us draw the graph.
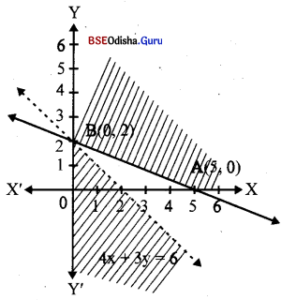
Step – 2 As 0(0, 0) does not satisfy 2x + 5y > 0 and x, y > 0 is the first quadrant, we have the shaded region is the feasible region whose vertices are A(5, 0) B(0, 2).
Step – 3 Z (5, 0) = 20
Z (0, 2) = 6 … Minimum
As the feasible region is unbounded. Let us draw the half plane.
4x + 3y < 6
| x | 0 | \(\frac{3}{2}\) |
| y | 2 | 0 |
Step – 4 As there is no point common to the feasible region and the half plane 4x + 3y < 6, we have Z is minimum for x = 0, y = 2 and Z(min) = 6
Question 6.
Find the feasible region of the system 2y – x > 0, 6y – 3x < 21, x > 0, y > 0. [2017 (A)
Solution:
Step – 1: Treating the constraints as equations we have
2y – x = 0
6y – 3x = 21
⇒ 2y – x = 0
2y – x = 7
Step – 2: Let us draw the lines.
Table – 1
| x | 0 | 2 |
| y | 0 | 1 |
| x | 1 | 37 |
| y | 4 | 5 |
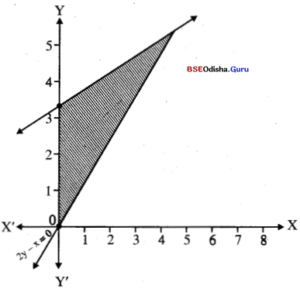
Step – 3: Clearly A(1, 3) Satisfies both the constraints, x > 0, y > 0 is the first quadrant. Thus the shaded region is the feasible region.
Question 7.
Solve the following LPP graphically:
Maximize: Z = 20x + 30y
Subject to: 3x + 5y ≤ 15
x, y ≥ 0. [2014 (A), 2016 (A), 2017 (A)
Solution:
Given LPP is
Maximize: Z = 20x + 30y
Subject to: 3x + 5y ≤ 15
x, y ≥ 0
Step – 1 Treating the constraints as equations we get 3x + 5y = 15.
Step- 2 Let us draw the graph
| x | 5 | 0 |
| y | 0 | 3 |
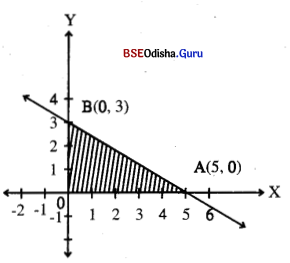
Step – 3
As 0(0, 0) satisfies 3x + 5y ≤ 15 the shaded region is the feasible region.
Step – 4
The vertices ofthe feasible region are 0(0, 0), A(5, 0) and B(0, 3).
Z(0) = 0, Z(A) = 100, Z(B) = 90
Z attains maximum at A for x = 5 and y = 0.
The given LPP has a solution, x = 5, y = 0 and Z(max) = 100.
Question 8.
Find the feasible region of the following system:
2x + y ≥ 6, x – y ≤ 3, x ≥ 0, y ≥ 0. [2016 (A)
Solution:
Given system of inequations are
2x + y ≥ 6, x – y ≤ 3, x ≥ 0, y ≥ 0
Step- 1: Consider 2x + y = 6
x – y = 3
Step – 2: Let us draw the graph
Table- 1
| x | 3 | 0 |
| y | 0 | 6 |
Table- 2
| x | 3 | 0 |
| y | 0 | -3 |
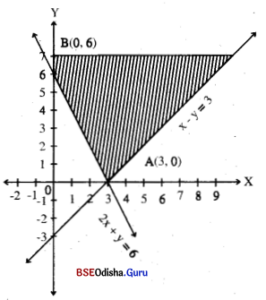
Step – 3: 0(0, 0) satisfies x – y < 3, does not satisfy 2x + y > 6 and x > 0, y > 0 is the first quadrant. Thus the shaded region is the feasible region.
![]()
Question 9.
Solve the following LPP graphically:
Minimize: Z = 6x1 + 7x2
Subject to: x1 + 2x2 ≥ 1
x1, x2 ≥ 0. [2015 (A)
Solution:
Given LPP is
Minimize: Z = 6x1+ 7x2
Subject to: x1 + 2x2 ≥ 2
x1, x2 ≥ 0
Let us draw the line x1 + 2x2 = 2
| x1 | 0 | 2 |
| x2 | 1 | 0 |
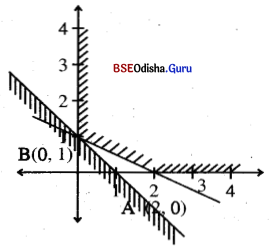
Clearly (0, 0) does not satisfy x1 + 2x2 ≥ 2 and x1, x2 ≥ 0 is the first quadrant.
The shaded region is the feasible region.
The coordinates of vertices are A(2, 0) and B(0, 1).
| Point | Z = 6x1 + 7x2 |
| A (2, 0) | 12 |
| B (0,1) | 7 → Minimum |
As there is no point common to the half plane 6x1 + 7x2 < 7 and the feasible region.
Z is minimum when x1 = 0, y1 =1 and the minimum value of z = 7
Question 10.
Find the feasible region of the following system:
2y – x ≥ 0, 6y – 3x ≤ 21, x ≥ 0, y ≥ 0. [2015 (A)
Solution:
Given system is
2y – x ≥ 0
6y – 3x ≤ 21
x, y ≥ 0.
Considering the constraints as equations we have
2y – x = 0
and 6y – 3x = 21
| x | 0 | 2 |
| x | 0 | 1 |
⇒ 3y – x = 7
| x | -7 | 2 |
| x | 0 | 3 |
Let us draw the lines
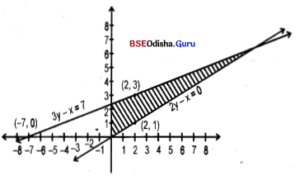
Clearly (2, 0) does not satisfy 2y – x ≥ 0 and satisfies 6y – 3x ≤ 21
∴ The shaded region is the feasible region.
Question 11.
Find the maximum value of z = 50x1 + 60x2
subject to 2x1 + 3x2 ≤ 6
x1, x2 ≥ 0. [2013 (A)
Solution:
Let us consider the constraints as equations.
2x1 + 3x2 = 6 … (1)
The table of some points on (1) is
| x1 | 0 | 3 |
| x2 | 2 | 0 |
Let us draw the line 2x1 + 3x2 = 6
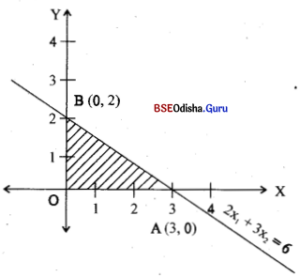
As (0, 0) satisfies the inequality 2x1 + 3x2 ≤ 6 and x1, x2 ≥ 0 is the first quadrant, the shaded region is the feasible region with corner points O(0, 0), A(3, 0) and B(0, 2).
| Corner point | z = 50x1 + 60x2 |
| O(0, 0) | 0 |
| A(3, 0) | 150 |
| B(0, 2) | 120 |
Thus Z(max) = 150 for x1 = 3, x2 = 0
Question 12.
Shade the feasible region satisfying the inequations 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 in a rough sketch. [2011(A)
Solution:
Let us consider the line 2x + 3y = 6
| x1 | 0 | 3 |
| x2 | 2 | 0 |
Let us draw the line on the graph
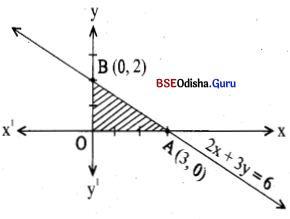
The feasible region is shaded in the figure.
Question 13.
Show the feasible region for the following constraints in a graph:
2x + y ≤ 4, x ≥ 0, y ≥ 0. [2010(A)
Solution:
Let us draw the graph of 2x + y = 4.
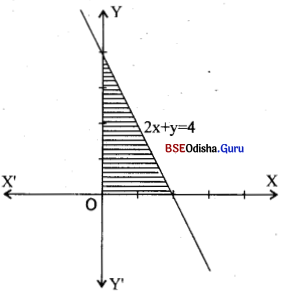
The shaded region shows the feasible region.
