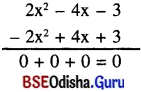BSE Odisha 8th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(a)

Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(a)

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର।
(i) 3x + 2x = (3 + ________)x = ________
(ii) 5x + 7x = (________ + 7)x = ________
(iii) -6x + 4x = {(________) + (________)}x = ________
(iv) -2x – 3x = {(________) + (________)}x = ________
(v) x – 2x = {(________) + (________)}x = ________
ସମାଧାନ :
(i) 3x + 2x
= (3 + 2)x
= 5x

(ii) 5x + 7x
= (5 + 7)x
= 12x

(iii) -6x + 4x
= {(-6) + (4)}x
= -2x

(iv) -2x – 3x
= {(-2) + (-3)}x
= -5x

(v) x – 2x
= {(1) + (-2)}x
= -x

Question 2.
ଯୋଗଫଳ ନିଶ୍ଚୟ କର।
(i) 4x ଓ 3x
(ii) 2x ଓ -3x
(iii) 3x ଓ -2x³
(iv) -5x² ଓ 2x²
(v) 4x ଓ -4
(vi) 2x² + 3 ଓ x² – 1
(vii) x² + 1 ଓ x – 1
(viii) x² + 3 + 2x ଓ x + 1
ସମାଧାନ :
(i) 4x + 3x
= (4 + 3)x
= 7x

(ii) 2x + (-3x)
= {2 + (-3)}x
= -x

(iii) (-3x³) + (-2x³)
= {(-3) + (-2)}x³
= -5x³

(iv) (-5x²) + 2x²
= (-5 + 2)x²
= -3x²

(v) 4x + (-4)
= 4x – 4 [ଏଠାରେ ଲକ୍ଷ୍ୟକର 4x ଓ -4 ଅସଦୃଶ ରାଶି]

(vi) 2x² + 3 + x² – 1
= 2x² + x² + 3 – 1
= (2 + 1)x² + 2
= 3x² + 2

(vii) x² + 1 + x – 1
= x² + x + 1 – 1
= x² + x
ବିକଳ୍ପ ପ୍ରଣାଳୀ : (ସ୍ତମ୍ଭ ପ୍ରଣାଳୀ)

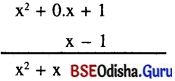
(viii) x² + 3 + 2x + x + 1
= x² + 2x + x + 3 + 1
= x² + (2 + 1)x + 4
= x² + 3x + 4
ବି.ଦ୍ର. : ସ୍ତମ୍ଭ ପ୍ରଣାଳୀରେ ମଧ୍ୟ ଏହାର ସମାଧାନ ସମ୍ଭବ।

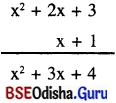
Question 3.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର।
(i) 3x + 2x = (________)
(ii) (________) + x = 8x
(iii) 2x + (________) = 6x
(iv) 3x + 4x = 4x + (________)
(v) 2x + 5x = (________) + 2x = (________)
(vi) 2x + 5y + z = (________) + z = (2x + z) + (________)
ସମାଧାନ :
(i) 3x + 2x = (5x)

(ii) (7x) + x = 8x

(iii) 2x + (4x) = 6x

(iv) 3x + 4x = 4x + (3x)

(v) 2x + 5x = (5x) + 2x = (7x)

(vi) 2x + 5y + z = (2x + 5y) + z = (2x + z) + (5y)

Question 4.
ଯୋଗଫଳ ନିଶ୍ଚୟ କର।
(i) 2x, 3x, 5x
(ii) 5x², x², 3x²
(iii) 2x³, 3x³, 4x³
(iv) 3x² + 2x ଓ x² + 3x
(v) x³ + 3 ଓ 4 – x² + x
(vi) 2x² + x – 2 ଓ x + 2
(vii) 5 – 2x + x² ଓ x² + 2x – 5
(viii) 3x – 2 + x² ଓ x² + 3x – 2
(ix) 1 + 2x² – 3x ଓ 2x + 3 + 4x²
(x) 2x² – 4x – 3 ଓ 4x + 3 – 2x²
ସମାଧାନ :
(i) 2x + 3x + 5x
= (2 + 3 + 5)x
= 10x

(ii) 5x² + x² + 3x²
= (5 + 1 + 3)x²
= 9x²

(iii) 2x³ + 3x³ + 4x³
= (2 + 3 + 4)x³
= 9x³
[(i), (ii) ଓ (iii) ରେ ବଣ୍ଟନ ନିୟମ ପ୍ରୟୋଗରେ ସଦୃଶ ପଦଗୁଡ଼ିକର ଯୋଗଫଳ କରାଯାଇଛି ।]

(iv) 3x² + 2x + x² + 3x
= 3x² + x² + 2x + 3x
= 4x² + 5x

(v) x³ + 3 + 4 – x² + x
= x³ – x² + x + 3 + 4
= x³ – x² + x + 7

(vi) 2x² + x – 2 + x + 2
= 2x² + x + x – 2 + 2
= 2x² + 2x

(vii) 5 – 2x + x² + x² + 2x – 5
= 5 – 5 – 2x + 2x + x² + x²
= 2x²
ବିକଳ୍ପ ପ୍ରଣାଳୀ :

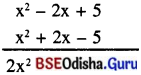
ଯୋଗଫଳ

(viii) 3x – 2 + x² + x² + 3x – 2
= x² + x² + 3x + 3x
= 2x² + 6x – 4
ବିକଳ୍ପ ପ୍ରଣାଳୀ : (ସ୍ତମ୍ଭ ପ୍ରଣାଳୀ)

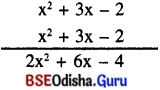
(ix) 1 + 2x² – 3x + 2x + 3 + 4x²
= 2x² + 4x² – 3x + 2x + 1 + 3
= 6x² – x + 4
ସ୍ତମ୍ଭ ପ୍ରଣାଳୀ :

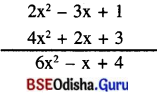
(x) 2x² – 4x – 3 + 4x + 3 – 2x²
= 2x² – 2x² – 4x + 4x – 3 + 3
= 0
ସ୍ତମ୍ଭ ପ୍ରଣାଳୀ :