CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Ex 6(d)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Ex 6(d) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Exercise 6(d)

Question 1.
State which of the following is the probability distribution of a random variable X with reasons to your answer:
(a)

X = x	0	1	2	3	4
p(x)	0.1	0.2	0.3	0.4	0.1

(b)

X = x	0	1	2	3
p(x)	0.15	0.35	0.25	0.2

(c)

X = x	0	1	2	3	4	5
p(x)	0.4	R	0.6	R2	0.7	0.3

Solution:
(a) As ∑p_i = 1.1 > 1, the given distribution is not a probability distribution.
(b) As ∑p_i = 0.95 < 1, the given distribution is not a probability distribution.
(c) As the value of R is not known, the given distribution is not a probability distribution.

Question 2.
Find the probability distribution of number of doublets in four throws of a pair of dice. Find also the mean and the variance of the number of doublets.
Solution:
Let the random variable X represents the number of doublets in 4 throws of a pair of dice.
X can take values 0, 1, 2, 3, 4
In a single throw of two dice
X can take values 0, 1, 2, 3, 4
In a single throw of two dice.
P(doublet) = \(\frac{6}{36}\)
P(non-doublet) = 1 – P (doublet) = \(\frac{5}{36}\)
Clearly the given experiment is a binomial experiment with n = 4,
p = \(\frac{1}{6}\), q = \(\frac{5}{6}\)

N.B. We can use the definition to find mean and variance.

Question 3.
Four cards are drawn successively with replacement from a well-shuffled pack of 52 cards. Find the probability distribution of the number of aces. Calculate the mean and variance of the number of aces.
Solution:
Let the random variable X denotes the number of aces.
Thus X can take values 0, 1, 2, 3, 4.
Clearly the given experiment is a binomial experiment with n = 4

N.B. We can use the definition to find mean and variance.

Question 4.
Find the probability distribution of
(a) number of heads in three tosses of a coin.
Solution:
Let the random variable X denotes the number of heads in three tosses of a coin.
X can take values 0, 1, 2, 3
In one toss p(H) = \(\frac{1}{2}\), p(T) = \(\frac{1}{2}\)
This experiment is a binomial experiment with n = 3, p = \(\frac{1}{2}\) and q = \(\frac{1}{2}\)

(b) number of heads in simultaneous tosses of four coins.
Solution:
When 4 coins tossed simultaneously, let the random variable X denotes the number of heads.
X can take values 0, 1. 2, 3, 4
This experiment is a binomial experiment with n = 4, p = \(\frac{1}{2}\) and q = \(\frac{1}{2}\)

Question 5.
A biased coin where the head is twice as likely to occur as the tail is, tossed thrice. Find the probability distribution of number of heads.
Solution:
Let in a toss P(T) = x
According to the question P(H) = 2x
Now 2x + x = 1
⇒ x = \(\frac{1}{3}\)
Thus P(T) = \(\frac{1}{3}\), P(H) = \(\frac{3}{3}\)
Clearly the given experiment is a binomial experiment with n = 3, p = P(H) = \(\frac{2}{3}\), q = P(T) = \(\frac{1}{3}\)
Let the random variable X denotes the number of heads in three throws of that coin.
X can take values 0, 1, 2, 3

Question 6.
Find the probability distribution of the number of aces in question no. 3 if the cards are drawn successively without replacement.
Solution:
Total number of cards = 52
Number of aces = 4
Number of cards drawn = 4 (one by one without replacement)
Let X = the random variable of number of aces drawn.
X can take values 0, 1, 2, 3 or 4

Question 7.
From a box containing 32 bulbs out of which 8 are defective 4 bulbs are drawn at random successively one after another with replacement. Find the probability distribution of the number of defective bulbs.
Solution:
Total number of bulbs = 32
Number of defective bulbs = 8
∴ Number of nondefective bulbs = 24
Number of bulbs drawn = 4 (one after another with replacement)
Clearly the experiment is a binomial experiment with n = 4
p = p ((drawing a defective bulb) = \(\frac{8}{32}\) = \(\frac{1}{4}\)
q = p (drawing a non defective bulb) = \(\frac{3}{4}\)
Let the random variable X denotes the number of defective bulbs.
∴ X can take values 0, 1, 2, 3, 4.

Question 8.
A random variable X has the following probability distribution.

X = x	0	1	2	3	4	5
p(x)	0	R	2R	3R	3R	R

Determine
(a) R
(b) P(X < 4)
(d) P(2 ≤ X ≤ 5)
(c) P(X ≥ 2)
Solution:
(a) Clearly ∑P_i = 1
⇒ R + 2R + 3R + 3R + R = 1

Question 9.
Find the mean and the variance of the number obtained on a throw of an unbiased coin.
Solution:
When an unbiased coin is tossed we donot get any number.
p(getting a number) = 0
Thus mean = variance = 0
If instead of coin it would be an unbiased die
Then let X = The number obtained in the throw.
X can take values 1, 2, 3, 4, 5 or 6.
P(X = 1) = P(X = 2) = P(X = 3) = P(X = 4)

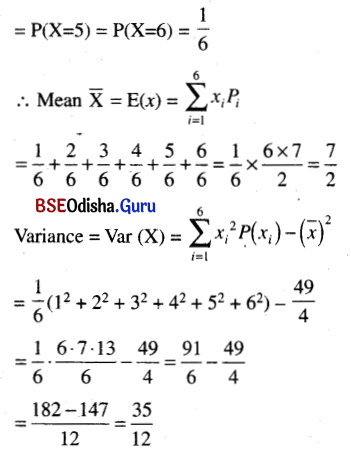
Question 10.
A pair of coins is tossed 7 times. Find the probability of getting
(i) exactly five tails
(ii) at least five tails
(iii) at most five tails
Solution:
Clearly the given experiment is a binomial experiment with

Question 11.
If a pair of dice is thrown 5 times then find the probability of getting three doublets.
Solution:
In a single through of a pair of dice
p (a doublet) = \(\frac{6}{36}\) = \(\frac{1}{6}\)
p (a non doublet) = 1 – p (a doublet) = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
Clearly the given experiment is a binomial experiment with n = 5
p = \(\frac{1}{6}\) and q = \(\frac{5}{6}\)
p(3 doublets in 5 throw) = ⁵C₃ p³q²
= 10. \(\left(\frac{1}{6}\right)^3\) \(\left(\frac{5}{6}\right)^2\) = \(\frac{250}{6^5}\) = \(\frac{125}{3888}\)

Question 12.
Four cards are drawn successively with replacement from a well-shuffled pack of 52 cards. What is the probability that:
(i) all the four cards are diamonds
(ii) only two cards are diamonds
(iii) none of the cards is a diamond.
Solution:
Out of 52 cards there are 13 diamonds. 4 cards are drawn one by one with replacement.
When we draw a card

Question 13.
In an examination, there are twenty multiple-choice questions each of which is supplied with four possible answers. What is the probability that a candidate would score 80% or more in the answers to these questions?
Solution:
Total number of questions = 20 for each question
p (correct answer) = \(\frac{1}{4}\)
p (wrong answer) = \(\frac{3}{4}\)
p (the score is > 80%)
= p (no. of correct answer > 16)
= p (16 correct answers)
+ p(17 correct answers)
+ p (18 correct answers)
+ p (19 correct answers)
+ p (20 correct answers)

Question 14.
A bag contains 7 balls of different colours. If five balls are drawn successively with replacement then what is the probability that none of the balls drawn is white?
Solution:
Total number of balls = 7 (The colours are different)
Number of balls drawn = 5 (one by one with replacement)
Case – 1
(If a white coloured ball is not present)
p(non is white) = 1
Case – 2
(If one ball is white).
In one draw p(white ball) = \(\frac{1}{7}\)
p (non white ball) = \(\frac{6}{7}\)
When 5 balls are drawn
p (none of the balls drawn is white) = ⁵C₀ \(\left(\frac{1}{7}\right)^0\) \(\left(\frac{6}{5}\right)^5\) = \(\left(\frac{6}{7}\right)^5\)

Question 15.
Find the probability ofthrowing at least 3 sixes in 5 throws of a die.
Solution:
In one throw of a die

Question 16.
The probability that a student securing first division in an examination is \(\). What is the probability that out of 100 students twenty pass in first division?
Solution:
Clearly the given experiment is a binomial experiment with

Question 17.
Sita and Gita throw a die alternatively till one of them gets a 6 to win the game. Find their respective probability of winning if Sita starts first.
Solution:
In one throw of a die
p (getting a 6) = \(\frac{1}{6}\)
p (not getting a 6) = \(\frac{5}{6}\)
If Sita begins the game she may win in first round or second round or third round, etc.
Thus p(Sita wins)

Question 18.
If a random variable X has a binomial distribution B(8, \(\frac{1}{2}\)) then find X for which the outcome is the most likely. [Hint: Find X=x for which P(X = x) is the maximum, x = 0, 1, 2, 3,…….. 8.]
Solution:
Given binomial distribution is B(8, \(\frac{1}{2}\))
Thus n = 8, p = \(\frac{1}{2}\), q = \(\frac{1}{2}\)
We shall find X which is most likely i.e. for which p(x = r) is maximum where r = 0, 1, 2, ….., 8
As p = q, the probability is maximum when ⁸Cr is maximum
But ⁸Cr, r = 0, 1, 2, ….. ,8 is maximum when r = 4.
Thus the most likely outcome is x = 4.