CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Ex 7(j)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(j) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(j)

Test differentiability and continuity of the following functions.
Question 1.
\(\left|1-\frac{1}{x}\right|\) at x = 1
Solution:

Question 2.
x² |x| at x = 0.
Solution:
Let f(x) = x² |x|
Then f(0) = 0

As L.H.D.=R.H.D., f(x) is differentiable at x = 0. We know that every differentiable function is continuous. So f(x) is also continuous at x = 0.

Question 3.
f(x) = tan x at x = \(\frac{\pi}{2}\)
Solution:
f(x) = tan x
f(\(\frac{\pi}{2}\)) = tan \(\frac{\pi}{2}\) which does not exist.
So f(x) is neither continuous not differentiable.

Question 4.
f(x) = cot x at x = \(\frac{\pi}{2}\).
Solution:

Question 5.
f(x) = |sin x| at x = π.
Solution:
Differentiability:
f(x) = |sin x|, x = π
f(π) |sin π| = 0

Question 6.
f(x) = latex]\frac{x}{1+|x|}[/latex] at x = 0
Solution:

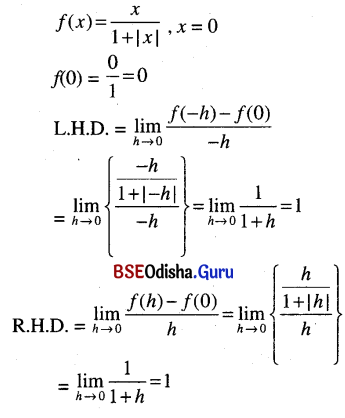
As L.H.D. = R.H.D., f(x) is differentiable at x = 0.
Every differentiable function is continuous.
So f(x) is also continuous at x = 0.

Question 7.
f(x) = \(\begin{cases}x \sin \frac{1}{x}, & x \neq 0 \\ 0, & x=0\end{cases}\) at x = 0
Solution:

Question 8.
f(x) = \(\begin{cases}\frac{1-e^{-x}}{x}, & x \neq 0 \\ 1 & x=0\end{cases}\) at x = 0
Solution:
f(0) = 1

As L.H.D. = R.H.D., f(x) is differentiable at the origin. Again every differentiable function is continuous. So f(x) is continuous at the origin.