CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Ex 9(d)

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(d) Textbook Exercise questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(d)

Question 1.
(i) ∫\(\frac{d x}{\sqrt{11-4 x^2}}\)
Solution:

(ii) ∫\(\frac{e^{3 x}}{\sqrt{4-e^{6 x}}}\)dx
Solution:

(iii) ∫\(\frac{d x}{\sqrt{25-(\ln x)^2}}\)
Solution:

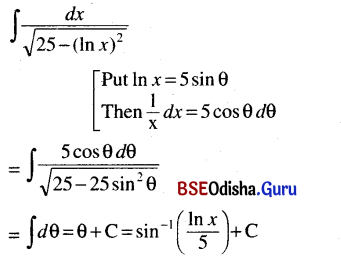
(iv) ∫\(\frac{\cos \theta}{\sqrt{4-\sin ^2 \theta}}\)dθ
Solution:

(v) ∫\(\frac{x^2}{\sqrt{36-x^6}}\)dx (x³ = z)
Solution:

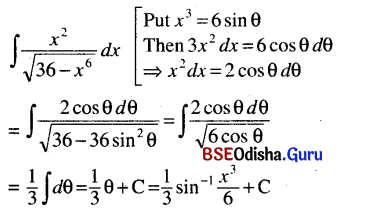
(vi) ∫\(\frac{x+3}{\sqrt{9-x^2}}\)dx
Solution:

(vii) ∫\(\frac{d x}{\sqrt{5-x^2-4 x}}\) (x + 2 = z)
Solution:

(viii) ∫\(\frac{x+3}{\sqrt{5-x^2-4 x}}\)dx
Solution:

Question 2.
(i) ∫\(\frac{d x}{3 x^2+7}\)
Solution:

(ii) ∫\(\frac{e^{4 x}}{e^{8 x}+4}\)dx (e^4x = z)
Solution:

(iii) ∫\(\frac{d x}{x\left\{(\ln x)^2+25\right\}}\)
Solution:

(iv) ∫\(\frac{\sec \theta \tan \theta}{\sec ^2 \theta+4}\)dθ
Solution:

(v) ∫\(\frac{x^9}{x^{20}+4}\)dx (x¹⁰ = z)
Solution:

(vi) ∫\(\frac{3 x+4}{x^2+4}\)dx
Solution:

(vii) ∫\(\frac{d x}{x^2+6 x+13}\) (x + 3 = z)
Solution:

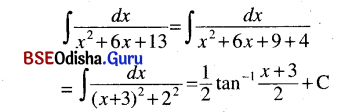
(viii) ∫\(\frac{x+5}{x^2+6 x+13}\)dx
Solution:

Question 3.
(i) ∫\(\frac{d x}{x \sqrt{4 x^2-9}}\)
Solution:

(ii) ∫\(\frac{d x}{\sqrt{e^{4 x}-5}}\) (e^2x = z)
Solution:

(iii) ∫\(\frac{d x}{x \ln x \sqrt{(\ln x)^2-4}}\)
Solution:

(iv) ∫\(\frac{\sec \theta d \theta}{\sin \theta \sqrt{3 \tan ^2 \theta-1}}\)
Solution:

(v) ∫\(\frac{d x}{x \sqrt{x^{14}-b^2}}\) (x⁷ = z)
Solution:

(vi) ∫\(\frac{x^2+3}{x \sqrt{x^2-4}}\)dx
Solution:

(vii) ∫\(\frac{d x}{(x+1) \sqrt{x^2+2 x-3}}\) (x + 1 = z)
Solution:

(viii) ∫\(\frac{x^2+2 x+4}{(x+1) \sqrt{x^2+2 x-3}}\) dx
Solution:

Question 4.
(i) ∫\(\frac{d x}{\sqrt{3 x^2+4}}\)
Solution:

(ii) ∫\(\frac{4 e^x}{\sqrt{3 e^x+4}}\)dx
Solution:

(iii) ∫\(\frac{d x}{x \sqrt{(\ln x)^2+8}}\)
Solution:

(iv) ∫\(\frac{d \theta}{\sin ^2 \theta \sqrt{\cot ^2 \theta+2}}\)
Solution:

(v) ∫\(\frac{x^2}{\sqrt{x^6+a^6}}\)dx
Solution:

(vi) ∫\(\frac{3 x+4}{\sqrt{5 x^2+8}}\)dx
Solution:

(vii) ∫\(\frac{e^x \cos e^x}{\sqrt{\sin ^2 e^x+9}}\)dx
Solution:

(viii) ∫\(\frac{2 x+11}{\sqrt{x^2+10 x+29}}\)dx (x + 5 = z)
Solution:

Question 5.
(i) ∫\(\frac{d x}{\sqrt{4 x^2-6}}\)
Solution:

(ii) ∫\(\frac{e^{5 x}}{\sqrt{e^{10 x}-4}}\)dx
Solution:

(iii) ∫\(\frac{d x}{x \sqrt{(\ln x)^2-4}}\); x > e²
Solution:

(iv) ∫\(\frac{\cos \theta d \theta}{\sin ^2 \theta \sqrt{{cosec}^2 \theta-4}}\)
Solution:

(v) ∫\(\frac{d x}{\sqrt{x} \sqrt{x-a^2}}\)
Solution:

(vi) ∫\(\frac{x-2}{\sqrt{3 x^2-8}}\)dx
Solution:

(vii) ∫\(\frac{3 x+4}{x \sqrt{2 x^2-5}}\)dx
Solution:

(viii) ∫\(\frac{x^2+2 x+2}{x \sqrt{x^2-4}}\)dx
Solution:

(ix) ∫\(\frac{d x}{\sqrt{x^2+8 x}}\)
Solution:

(x) ∫\(\frac{x+7}{\sqrt{x^2+8 x}}\)dx
Solution: