BSE Odisha 10th Class Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(c)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(c)

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ଠିକ୍ ଉତ୍ତର ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :
(i) △ABC ଓ △DEF ମଧ୍ୟ 6ର , m∠A = m∠D, m∠B = m∠E, AB = 3 ସେ.ମି., , BC = 5 ସେ.ମି.,ଏବଂ DE = 7.5 ସେ.ମି. ହେଲେ,, EF : _____ ସେ.ମି., (10, 10.5, 12, 12.5)
Solution:
12.5
Hint:
△ABC ~ △DEF ⇒ \(\frac { AB }{ DE }\) = \(\frac { BC }{ EF }\) ⇒ \(\frac { 3 }{ 7.5 }\) = \(\frac { 5 }{ EF }\) ⇒ EF = 12.5 ସେ.ମି. |

(ii) △ABC ରେ AB = 5 6 ସେ.ମି., BC = 7 ସେ.ମି., CA = 8 6 ସେ.ମି.; △PQR ରେ PQ = 10 ସେ.ମି., QR = 14 ସେ.ମି. । PR = _____ ସେ.ମି. ହେଲେ, △ABC ଓ △PQR ସଦୃଶକୋଣୀ ହେବେ । (12, 16, 20, 24)
Solution:
16
Hint:
△ABC ~ △PQR ⇒ \(\frac { AB }{ PQ }\) = \(\frac { BC }{ QR }\) ⇒ \(\frac { AC }{ PR }\)

(iii) △ABC ଓ △POR ମଧ୍ଯରେ ∠B ≅ ∠Q | △ABC ର AB = 8 ସେ.ମି. ଏବଂ BC = 12 ସେ.ମି. । A POR ର PQ = 12 ସେ.ମି. ଏବଂ QR = 18 ସେ.ମି. । △ABC ର କ୍ଷେତ୍ରଫଳ 48 ବର୍ଗସେ.ମି. ହେଲେ △PQR ର କ୍ଷେତ୍ରଫଳ = _____ ସେ.ମି. ହେଲେ, (84, 96, 104, 108)
Solution:
108
Hint:
△ABC ~ △PQR
∴ \(\frac { △ABC ର 6ସ୍ତୃତ୍ତ୍ଵଫଳ }{ △PQR ର 6ସ୍ତୃତ୍ତ୍ଵଫଳ }\) = \(\frac{\mathrm{AB}^2}{\mathrm{PQ}^2}\)
⇒ \(\frac { 48 }{ △PQR ର 6ସ୍ତୃତ୍ତ୍ଵଫଳ }\) = \(\frac { 4 }{ 9 }\)
⇒ △PQR ର 6ସ୍ତୃତ୍ତ୍ଵଫଳ = 108 ଦ . ସେ.ମି.

(iv) △ABC ଓ ∠ABC ର ସମଦ୍ୱିଖଣ୍ଡକ \(\overline{\mathrm{AC}}\) କୁ P ଦିନ୍ଦୁ6ର ଛେଦ କରେ | AB = 12 ସେ.ମି. ଓ BC = 9 ସେ.ମି. ହେବେ , AP : AC _____ | (4 : 3, 3 : 4, 7 : 4, 4 : 7)
Solution:
4 : 7
Hint:
∠B ର ସମଦ୍ୱିଖଣ୍ଡନ \(\overline{\mathrm{BP}}\)
⇒ \(\frac { AB }{ BC }\) = \(\frac { AP }{ PC }\) ⇒ \(\frac { 4 }{ 3 }\) = \(\frac { AP }{ PC }\)
∴ \(\frac { AP }{ AC }\) = \(\frac { 4 }{ 7 }\)

(v) ଦୁଇଟି ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ 16 : 25 ହେଲେ, ସେହି ତ୍ରିଭୁଜ ଦ୍ଵୟର ଅନୁରୂପ ଯୋଡ଼ାର ଦୈର୍ଘ୍ୟର ଅନୁପାତ _____ | (4 : 5, 2 : 5, 5 : 4, 5 : 2)
Solution:
4 : 5
Hint:
ଦୁକଟି ସମବାହୁ ତିଦୁକର 6ସ୍ତୃତ୍ରଫଳର ଅନ୍ନପାଜର ଦାହୁଦୂଯର ତାଦଣପୁର ବ୍ରଣ ଅନ୍ମଣ ପର ସହ ସମାନ |

(vi) ପାଣ୍ଡଷ୍ଟ ଚିତ୍ରରେ , m∠B = 50°, m∠BDC = 100° ଓ △DBC ~ △CBA ହେଲେ , m∠ACD ______ | (60°, 70°, 80°, 90°)

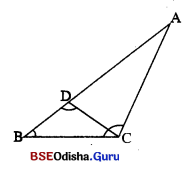
Solution:
70°
Hint:
△DBC ~ △CBA
⇒ m∠BDC = m∠ACB = 100° କକ୍ମ m∠BCD = 30°
∴ m∠ACD = 70°

(vii) ପାଣ୍ଡଷ୍ଟ ଚିତ୍ରରେ , △ABE ଓ △ACD ର 6ସ୍ତ୍ ତ୍ରଫଳ ସମାଜ 6 ଦୃ6କ , △BOC ~ _____ |

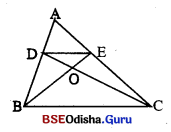
(△ADE, △DOB, △EOD, △OEC)
Solution:
△EOD
Hint:
△ABE 6ସ୍ତୃତ୍ତ୍ଵଫଳ = D ACD 6ସ୍ତୃତ୍ତ୍ଵଫଳ ⇒ △BDE 6ସ୍ତୃତ୍ତ୍ଵଫଳ = △DEC 6ସ୍ତୃତ୍ତ୍ଵଫଳ ⇒ \(\overline{\mathrm{DE}}\) || \(\overline{\mathrm{BC}}\) ⇒ △BOC ~ △EOD

(viii) ପାଶ୍ଚଣ୍ଠ ଚିତ୍ରରେ △ABC ର \(\overline{\mathrm{AE}}\) ଓ \(\overline{\mathrm{BD}}\) ଯଥାକୃ6ମ \(\overline{\mathrm{BC}}\) ଓ \(\overline{\mathrm{AC}}\) ପୃତି ଦିପତାତ ଶାସ୍ତ୍ର ଦିନ୍ଦରୁ କମ , 6ତ6ଦ △BEM ~ △ ___ |

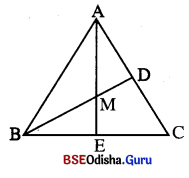
[BEA, ABD, BDC, AEC]
Solution:
△AEC
Hint:
m∠EBM = m∠EAC ଏବଂ m∠MEB = m∠AEF
⇒ △BEM ~ △AEC

(ix) ପାସ୍ତସ୍ଥ ଚିତ୍ର6ର BC ରପରିସ୍ଥ D ଏକ ଦନ୍ଦୁ |
∠ADC ≅ ∠BAC ତ୍ରଫଳ ,
CB. CD = _____

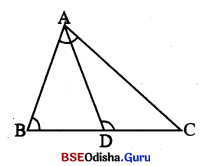
(AC² , AB² , AD . AB, AD. AC)
Solution:
AC²
Hint:
△ABC ~ △DAC ⇒ \(\frac { CB }{ AC }\) = \(\frac { AC }{ CD }\)
⇒ CB . CD = AC²

(x) △ABC ରେ ∠BAC ର ସମଦିଖଣ୍ଡକ BC କୁ M ଦିନ୍ଦୁ6ର ଛେଦକ6ର | AB : AC = 2 : 3 ଏବଂ BC = 15 ସେ.ମି. ହେଲେ, , BM = _____ ସେ.ମି. | (6, 9, 10, 12)
Solution:
6
Hint:
\(\frac { AB }{ AC }\) = \(\frac { BM }{ MC }\) (∠BAC ର ସମଦ୍ୱିଗଣ୍ଡକ \(\overline{\mathrm{AM}}\))
⇒ \(\frac { 2 }{ 3 }\) = \(\frac { BM }{ MC }\)
⇒ BC = BM + MC ⇒ 15 = 2x + 3x ⇒ x = 3, BM = 6

Question 2.
(i)△ABC ରେ AB = 2.5 ସେ.ମି., BC = 2 ସେ.ମି., AC = 3.5 ସେ.ମି. ଏବଂ △PQR 66 PQ = 5 ସେ.ମି. QR = 4 ସେ.ମି. , PR = 7 ସେ.ମି. | m∠A = x° ଓ m∠Q = y° ଛେଦକ, m∠B, m∠C, m∠P ଓ m∠R ହେଲେ କୁର |
Solution:

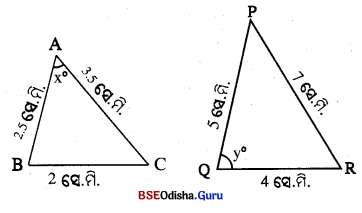
ଏO|6ର \(\frac { AB }{ PQ }\) = \(\frac { 2.5 }{ 5 }\) = \(\frac { 1 }{ 2 }\) , \(\frac { BC }{ QR }\) = \(\frac { 2 }{ 4 }\) = \(\frac { 1 }{ 2 }\) ଓ \(\frac { AC }{ PR }\) = \(\frac { 3.5 }{ 7 }\) = \(\frac { 1 }{ 2 }\)
⇒ \(\frac { AB }{ PQ }\) = \(\frac { BC }{ QR }\) = \(\frac { AC }{ PR }\) ⇒ △ABC ~ △PQR
⇒ m∠A = m∠P = x° , m∠B = m∠Q = y°
m∠C = 180° – (x – y)° = m∠R |

(ii) △ABC ଓ △DEF 68 ∠B ≅ ∠E, AB = 4 ସେ.ମି., BC = 6 ସେ.ମି., EF = 9 ସେ.ମି. ଓ DE = 6 ସେ.ମି. | △ABC ର ଶ୍ରେତ୍ରଫଳ 20 ଦଗ ସେ.ମି.ଦ୍ରେଭେ , DEF ର ଶ୍ରେତ୍ରଫଳ ନିଗ୍ରଯ କର |
Solution:

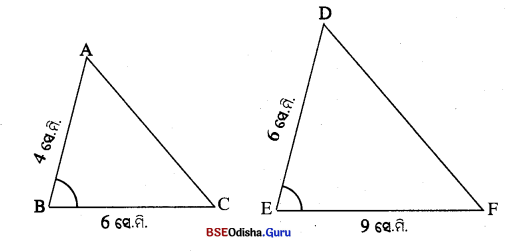
\(\frac { AB }{ DE }\) = \(\frac { 4 }{ 6 }\) = \(\frac { 2 }{ 3 }\)
\(\frac { BC }{ EF }\) = \(\frac { 6 }{ 9 }\) = \(\frac { 2 }{ 3 }\)
∴ \(\frac { AB }{ DE }\) = \(\frac { BC }{ EF }\) = ଓ ∠B ≅ ∠E
⇒ △ABC ~ △DEF
⇒ \(\frac { △ABC ର ଶ୍ରେତ୍ରଫଳ }{ △DEF ର ଶ୍ରେତ୍ରଫଳ }\) = \(\frac{\mathrm{AB}^2}{\mathrm{DE}^2}\) = \(\frac { 4 }{ 9 }\)
⇒ \(\frac { 20 ବଗ 6ସ.ମି. }{ △DEF ର 6ଘ୍ତତ୍ରଫଳ }\) = \(\frac { 4 }{ 9 }\)
⇒ △DEF ର 6ଘ୍ତତ୍ରଫଳ = \(\frac { 20 × 9 }{ 4 }\) ଚ୍ଚଗ ସେ.ମି. = 45 ଦଗ6ସ.ମି. |

(iii) ଦୁଇଟି ସଦୃଶ ତ୍ରିଭୁଜ ମଧ୍ୟରୁ ପ୍ରଥମଟିର କ୍ଷେତ୍ରଫଳ ଦ୍ବିତୀୟଟିର କ୍ଷେତ୍ରଫଳର 9 ଗୁଣ ହେଲେ, ତ୍ରିଭୁଜ ଦୁଇଟିର ଅନୁରୂପ ବାହୁଦ୍ୱୟର ଅନୁପାତ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ତ୍ରିଭୁଜଦ୍ୱୟର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ = 9 : 1 = ତ୍ରିଭୁଜଦ୍ଵୟର ଅନୁରୂପ ବାହୁ ।
⇒ ତ୍ରିଭୁଜଦ୍ଵୟର ଅନୁରୂପ ବାହୁ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ବର୍ଗାନୁପାତ = \(\sqrt{9^2}\) : \(\sqrt{1^2}\) = 3 : 1

(iv) ପାଣ୍ସ୍ଟଣ ଚିତ୍ର6ର , ∠BAC ≅ ∠DAC , AC = 12 6ସ.ମି. ଓ BC = 15 6ସ.ମି. | △ADC ର ଷ୍ଟେତୃଫକ 32 ଦ.6ସ.ମି. 6ଦୃ6କ , △ABD ର ଷ୍ଟେତୃଫକ ଚିତ୍ର6ର କର |

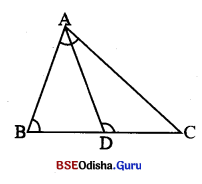
Solution:
△ABC ଓ △DAC ମଧ୍ୟ6ର
∠BAC ≅ ∠DAC (ଦର)
∠ACB ≅ ∠ACD (ସାଧାରଣ 6କାଣ)
ଥଦଣଘ୍ତ ∠ACB ≅ ∠DAC

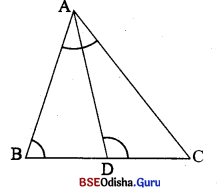
∴ △ABC ~ △DAC (6କା – 6କା – 6କା ସାଧାରଣ)
⇒ \(\frac { △ABC ର ଷ୍ଟେତୃଫକ }{ △DAC ର ଷ୍ଟେତୃଫକ }\) = \(\frac { △ABC ର ଷ୍ଟେତୃଫକ }{ 32 ପରିସାମା }\) = \(\frac{\mathrm{BC}^2}{\mathrm{AC}^2}\) = \(\frac{15^2}{12^2}\)
⇒ △ABC ର ଷ୍ଟେତୃଫକ = (\(\frac { 225 }{ 144 }\) × 32 ) ପରିସାମା = 50 ପରିସାମା |
△ABD ର ଷ୍ଟେତୃଫକ = △ABC ର ଷ୍ଟେତୃଫକ – △ADC ର ଷ୍ଟେତୃଫକ = 50 ପରିସାମା – 32 ପରିସାମା = 18 ଦ.6ସ.ମି.

(v) △ABC ର AB = 5 6ସ.ମି., BC = 7 6ସ.ମି.. ଓ CA = 9 6ସ.ମି. | △PQR ~ △ABC ଏବଂ △PQR ର ପରିସାମା 63 6ସ.ମି. ହୋ6କ , PQ, QR ଓ PR କିଣ୍ଡଯ କର |
Solution:
△PQR ~ △ABC (ଦଉ)
△ABC ର ପରିସାମା = (5 + 7 + 9 ) 6ସ.ମି. = 21 6ସ.ମି.
\(\frac { △PQR ର ଷ୍ଟେତୃଫକ }{ △ABC ର ଷ୍ଟେତୃଫକ }\) = \(\frac { 63 }{ 21 }\) = 3 (△PQR ର ପରିସାମା = 63 6ସ.ମି. )
⇒ \(\frac { △PQR ର ଷ୍ଟେତୃଫକ }{ △ABC ର ଷ୍ଟେତୃଫକ }\) = \(\frac{\mathrm{PQ}+\mathrm{QR}+\mathrm{PR}}{\mathrm{AB}+\mathrm{BC}+\mathrm{AC}}\) = \(\frac { PQ }{ AB }\) = \(\frac { QR }{ BC }\) = \(\frac { PR }{ AC }\)
⇒ 3 = \(\frac { PQ }{ 5 }\) = \(\frac { QR }{ 7 }\) = \(\frac { PR }{ 9 }\)
∴ PQ = 5 × 3 6ସ.ମି. = 15 6ସ.ମି. , QR = 7 × 3 6ସ.ମି. = 21 6ସ.ମି. PR = 9 × 3 6ସ.ମି. = 27 6ସ.ମି. |

(vi) △ABC ~ △PQR ; AB = 5 6ସ.ମି. , BC = 12 6ସ.ମି. ., AC = 13 6ସ.ମି. ଓ QR = 8 6ସ.ମି. ସମଦ୍ୱିଗଣ୍ଡକ △PQR ର ଷ୍ଟେତୃଫକ ଚିତ୍ର6ର କର |
Solution:
△ABC ~ △PQR(ଦଉ)
\(\frac { △ABC ର ଷ୍ଟେତୃଫକ }{ △PQR ର ଷ୍ଟେତୃଫକ }\) = \(\frac{\mathrm{BC}^2}{\mathrm{QR}^2}\) = \(\frac { 144 }{ 64 }\) = \(\frac { 9 }{ 4 }\)
(ତ୍ରିଭୁଜଦ୍ୱୟର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ, ସେମାନଙ୍କର ଅନୁରୂପ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନୁପାତ ସହ ସମାନ ।)
ଆମେ ଜାଣୁ 5² + 12² = 13² ଅର୍ଥାତ୍ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ । m∠ABC = 90°
∴△ABC ର ଷ୍ଟେତୃଫକ = \(\frac { 1 }{ 2 }\) × 5 × 12 6ସ.ମି = 30 6ସ.ମି²
\(\frac { 30 6ସ.ମି^2 }{ △PQR ର ଷ୍ଟେତୃଫକ }\) = \(\frac { 9 }{ 4 }\)
⇒ △PQR ର ଷ୍ଟେତୃଫକ = \(\frac { 30 × 4 }{ 9 }\) 6ସ.ମି² = 13\(\frac { 1 }{ 3 }\) 6ସ.ମି²|

(vii) △ABC ~ △PQR | △ABC ପରିସୀମା 60 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ 81 ବର୍ଗ ସେ.ମି. ଏବଂ △PQR ର ପରିସୀମା 80 ସେ.ମି. ହେଲେ, ଏହାର କ୍ଷେତ୍ରଫଳ କେତେ ?
Solution:
△ABC ~ △PQR (ଦଉ)
\(\frac { △ABC ର ପରିସୀମା }{ △PQR ର ପରିସୀମା }\) = \(\frac { 60 ସେ.ମି. }{ 80 ସେ.ମି. }\) = \(\frac { 3 }{ 4 }\)
⇒ \(\frac { AB }{ PQ }\) = \(\frac { 3 }{ 4 }\)
∴ \(\frac { △ABC ର କ୍ଷେତ୍ରଫଳ }{ △PQR ର କ୍ଷେତ୍ରଫଳ }\) = \(\frac{3^2}{4^2}\) = \(\frac { 9 }{ 16 }\)
⇒ \(\frac { 81 30 6ସ.ମି^2 }{ △PQR ର କ୍ଷେତ୍ରଫଳ }\) = \(\frac { 9 }{ 16 }\) ⇒ △PQR ର କ୍ଷେତ୍ରଫଳ = \(\frac { 81 × 16 }{ 9 }\) 6ସ.ମି² = 144 6ସ.ମି² .

Question 3.
ପ୍ତମାଣ କର 6ଯ କୁଲଟି ସହଶ ତ୍ରରୁଜର
(a) ଅନୁରୂପ ଉଚ୍ଚତାମାନଙ୍କର ଦୈର୍ଘ୍ୟ, ଉକ୍ତ ତ୍ରିଭୁଜ ଦ୍ୱୟର ଅନୁରୂପ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସହ ସମାନୁପାତୀ ।

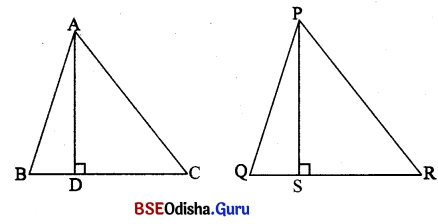
Solution:

Question 4.
ଦୁଇଟି ସଦୃଶ ତ୍ରିଭୁଜର ପରିସୀମା ସମାନ ହେଲେ, ପ୍ରମାଣ କର ଯେ ତ୍ରିଭୁଜ ଦୁଇଟି ସର୍ବସମ ।
Solution:

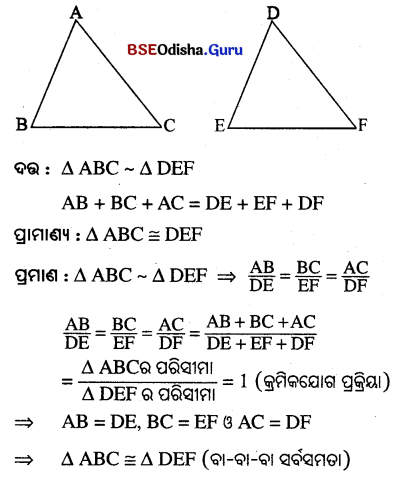
Question 5.
ଦୁଇଟି ସଦୃଶ ତ୍ରିଭୁଜର ପରିସୀମା ସମାନ ହେଲେ, ପ୍ରମାଣ କର ଯେ ତ୍ରିଭୁଜ ଦୁଇଟି ସର୍ବସମ ।
Solution:

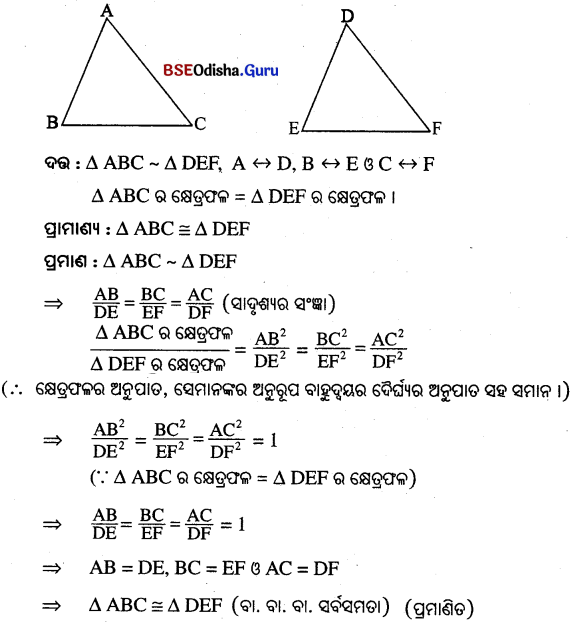
Question 6.
ପ୍ରମାଣ କର : ଦୁଇଟି ସଦୃଶ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ, ଉକ୍ତ ତ୍ରିଭୁଜ ଦ୍ଵୟର
(a) ଅନ୍ତୁପ ଭରତାମାନକର 6ବିଶଇ ଦଗାନ୍ ପାତ ସହ ସମାନ |
Solution:

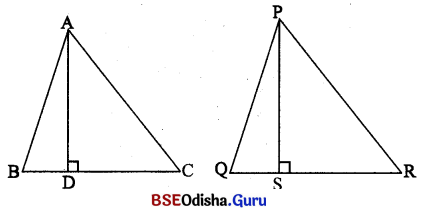
ଦଭ : △ABC ~ △PQR , A <-> P, B <-> Q ଓ C <-> R
\(\overline{\mathrm{AD}}\) ⊥ \(\overline{\mathrm{BC}}\) ଓ \(\overline{\mathrm{PS}}\) ⊥ \(\overline{\mathrm{QR}}\)
ପ୍ତ।ମାଣୟ : \(\frac { △ABCରଶ୍ରେତ୍ରଫଳ }{ △PQRରଶ୍ରେତ୍ରଫଳ }\) = \(\frac{\mathrm{AD}^2}{\mathrm{PS}^2}\)
ପ୍ତମାଣ : △ABD ଓ △PQR ରେ ∠ABD ≅ ∠PQS (∵ ∠ABC ≅ ∠PQR)
∠ADB ≅ ∠PSQ (ଇବ6ପ୍ ସମ6କାଣ)
ଅତ୍ଣିପ୍ରତି ∠BAD ≅ ∠QPS
△ABD ଓ △PQS (6କା. 6କା. 6କା. ସାଦ୍ଶ୍ୟ)
⇒ \(\frac { AB }{ PQ }\) = \(\frac { AD }{ PS }\) (ସାଦ୍ୱଣଦର ଫଲ୍ଲା)
△ABC ~ △PQR ⇒ \(\frac { AB }{ PQ }\) = \(\frac { BC }{ QR }\) = \(\frac { AC }{ PR }\)
∴ \(\frac { AB }{ PQ }\) = \(\frac { BC }{ QR }\) = \(\frac { AC }{ PR }\) = \(\frac { AD }{ PS }\)
\(\frac { △ABCରଶ୍ରେତ୍ରଫଳ }{ △DEFରଶ୍ରେତ୍ରଫଳ }\) = \(\frac{\mathrm{AB}^2}{\mathrm{PQ}^2}\) = \(\frac{\mathrm{BC}^2}{\mathrm{QR}^2}\) = \(\frac{\mathrm{AC}^2}{\mathrm{PR}^2}\) = \(\frac{\mathrm{AD}^2}{\mathrm{PS}^2}\) (ପ୍ତମାଣିତ)

(b) ଅନୁରୁପ 6ଲାଣ-ସମଦ୍ଦିଖଣନମାନକର 6ବିଣ୍ୟର 6ବଣ୍ୟର ତାଗାନ୍ପାତ ସହ ପାପନ |
Solution:

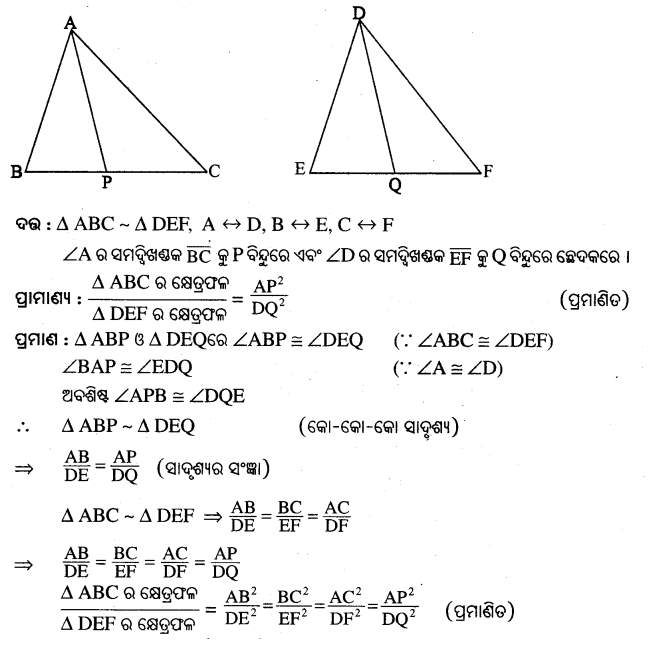
(c) ଅନୁରୁପ 6ଲାଣ-ସମଦ୍ଦିଖଣନମାନକର 6ବିଣ୍ୟର 6ବଣ୍ୟର ତାଗାନ୍ପାତ ସହ ପାପନ |
Solution:

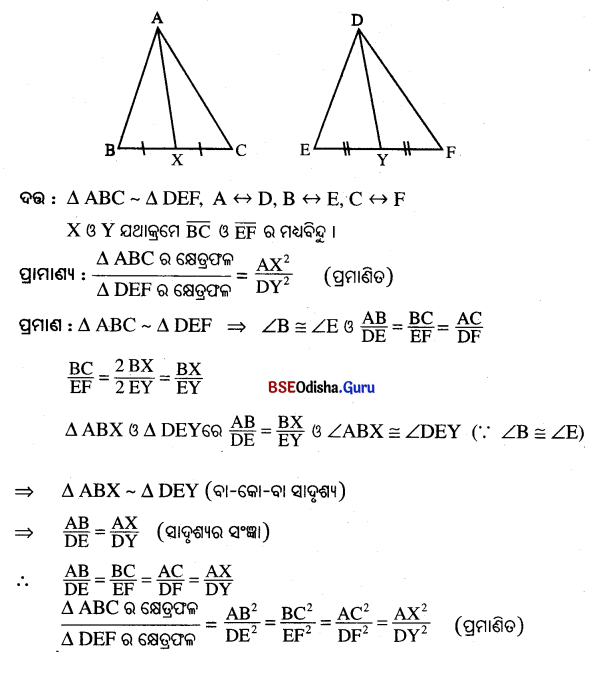
(d) ଅନୁରୁପ 6ଲାଣ-ସମଦ୍ଦିଖଣନମାନକର 6ବିଣ୍ୟର 6ବଣ୍ୟର ତାଗାନ୍ପାତ ସହ ପାପନ |
Solution:

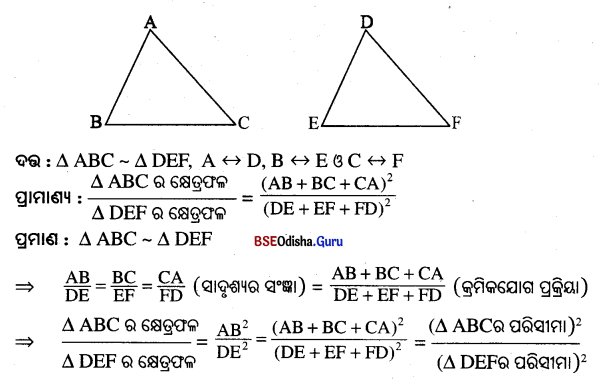
Question 7.
△ABC ର \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{AC}}\) ଢାଦୁ ଭଜଟି ଦିନ୍ଦୁ 6ଯପରିକି △BQP ଓ △CPQ ସମ6ଷତ୍ରଫଳ ଦିଣିସ୍ତୃ | ପ୍ରମାଣ କର ଯେ \(\frac { PQ }{ BC }\) = \(\frac { AP }{ AB }\) |

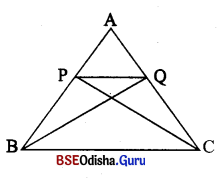
Solution:

Question 8.
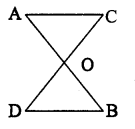
ନିମ୍ନ ଚିତ୍ରରେ \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{CD}}\) ର 6ଛଦଦିନ୍ଦୁ O |
(a) AO. OD = BO. OC 6ହକେ , ପୃମାଣ କର ଯେ △AOC ~ △BOD |
(b) CO. OD = AO. OB 6ହକେ , ପୃମାଣ କର ଯେ △AOC ~ △DOB |
(c) ପୃଦତରା 6କରି ପେଣ \(\overline{\mathrm{AC}}\) ଓ \(\overline{\mathrm{DB}}\) ସମାତୃର 6ଦୃ6ଦ ?

Solution:

Question 9.
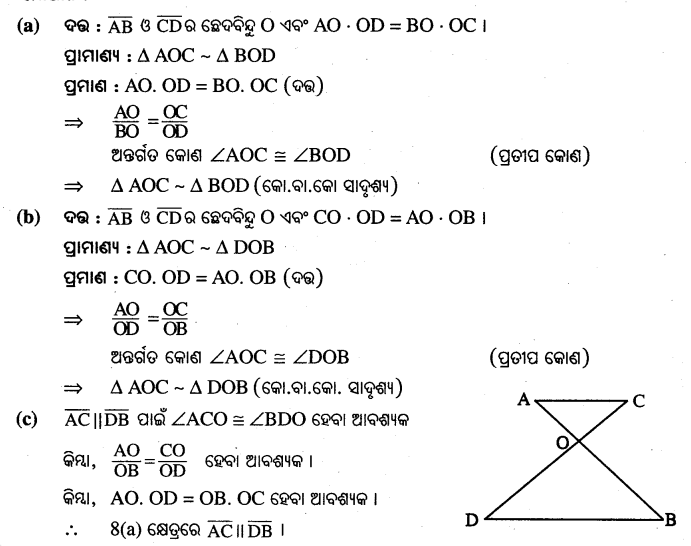
ABCD ଟ୍ରାପିଜିଯମ୍ବର \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{DC}}\) | କଣ୍ଡ \(\overline{\mathrm{AC}}\) s \(\overline{\mathrm{BD}}\) ପରଘରକୁ O ଦିନ୍ଦୁ6ର ଛେଦ କରତି | AO = 3 6ପ.ମି. ଏବଂ OC = 5 6ପ.ମି. | △AOB ର ଘେତ୍ରଫଳ 36 ଦ. 6ପ.ମି. ହେଲେ , △COD ର ଘେତ୍ରଫଳ କିଣ୍ଡଯ କର |
Solution:

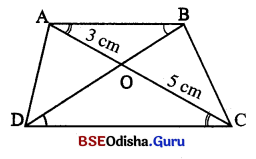
ABCD ଟ୍ଟାପିଳିଯମ୍ନରେ \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{DC}}\) |
\(\overline{\mathrm{AC}}\) ଓ \(\overline{\mathrm{BD}}\) ର ଛେଦଦିନ୍ଦୁ O |
∠ABO ≅∠ODC (ଏକାନ୍ତର 6କାଣ)
∠BAO ≅∠OCD (ଏକାନ୍ତର 6କାଣ)
∠AOB ≅∠COD (ପ୍ତତାପ 6କାଣ)
⇒ △AOB ~ △COD (6କା. 6କା. 6କା. ସାଦ୍ଶ୍ୟ)
⇒ \(\frac { △AOBରଶ୍ରେତ୍ରଫଳ }{ △CODରଶ୍ରେତ୍ରଫଳ }\) = \(\frac{\mathrm{AO}^2}{\mathrm{OC}^2}\)
⇒ \(\frac { 36 ଦଗ ସେ.ମି. }{ △CODରଶ୍ରେତ୍ରଫଳ }\) = \(\frac { 9 }{ 25 }\)
⇒ △COD ର ଶ୍ରେତ୍ରଫଳ = \(\frac { 36 × 25 }{ 9 }\) ଦଶ6ସ.ମି. = 100 ଦଶ6ପ.ମି. |

Question 10.
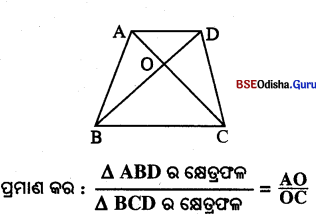
କିମ୍ନ ଚିତ୍ର6ର △ABC ଓ △DBC ଭଉଯ ଏକ ରମି \(\overline{\mathrm{BC}}\) ଭପରିଷ୍ଟ | \(\overline{\mathrm{AC}}\) ଓ \(\overline{\mathrm{BD}}\) ର 6ଛବଦିହୁ O 6ହ6ଲ ,

Solution:

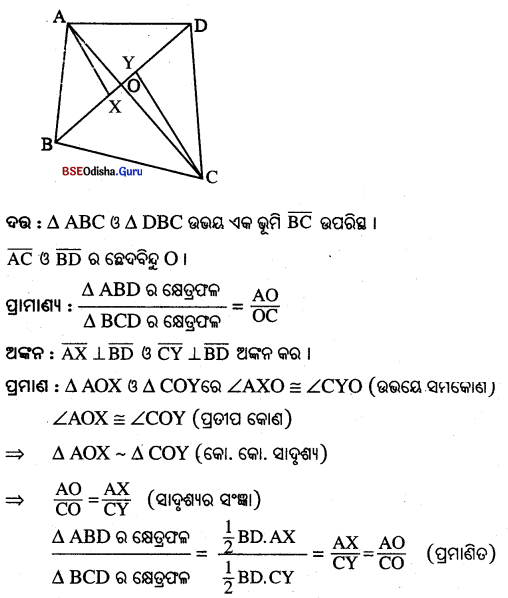
Question 11.
ପ୍ରମାଣ କର ଯେ ଏକ ତ୍ରିଭୁଜର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁର ସଂଯୋଜକ ରେଖାଖଣ୍ଡମାନଙ୍କ ଦ୍ୱାରା ତ୍ରିଭୁଜଟି ଯେଉଁ ଚାରୋଟି ତ୍ରିଭୁଜରେ ପରିଣତ ହୁଏ, ସେମାନେ ସର୍ବସମ ଓ ପ୍ରତ୍ୟେକ ମୂଳ ତ୍ରିଭୁଜ ସହ ସଦୃଶ । ପୁନଶ୍ଚ ପ୍ରମାଣ କର ଯେ ଉତ୍ପନ୍ନ ହୋଇଥିବା ପ୍ରତ୍ୟେକ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ, ମୂଳତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଏକ ଚତୁର୍ଥାଂଶ ।
Solution:

Question 12.
ପାଣମ୍କ ଟିତ୍ରଭେ , △ABC ର ∠ABC ଏକ ସମ6କାଣ | PQRS ଏକ ଥାଯତରିତ୍ର 6ତ୍ର6କ ଯେ,
△APS ~ △QCR ~ △PQB ~ △ACB |
Solution:

Question 13.
ABCD ଟାପିକଯମ୍6ର \(\overline{\mathrm{AD}}\) || \(\overline{\mathrm{BC}}\) | ∠ABD ≅ ∠DCB 6ଦୁ6କ , ପ୍ତମାଣକର ପେ BD = AD. BC |
Solution:

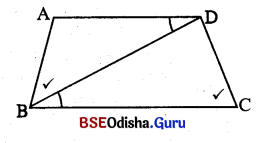
ଦର : ABCD ଟ୍ରାପିଚ୍ଚିଯମ୍6ର \(\overline{\mathrm{AD}}\) || \(\overline{\mathrm{BC}}\)
ଏଣ ∠ABC ≅ ∠DCB |
ସ୍ତ।ମାଶ୍ୟ : BC² = AD. BC
ପ୍ତମାତ : \(\overline{\mathrm{AD}}\) || \(\overline{\mathrm{BC}}\)
⇒ ∠ADB ≅∠DCB (ଏକାତ୍ରଉ 6କାଣ)
∠ADB ≅∠DCB (ଦଭ)
⇒ △ABD ~ △DCB (6କା. 6କା. 6କା. ସାଦ୍ଶ୍ୟ)
⇒ \(\frac { BD }{ BC }\) = \(\frac { AD }{ BD }\) (ପlଦୃଶ୍ୟର ଫଳା)
⇒ BD² = BC. AD

Question 14.
ନପ୍ ଟିତ୍ର6ର \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{DC}}\) | △ADO ~ △BCO ବ୍ରେକେ , ପ୍ରମାଣ କର AD = BC |
(ସୂଚନା : ପ୍ରଶ୍ନ 5ରେ ପ୍ରମାଣିତ ତଥ୍ୟକୁ ବ୍ୟବହାର କର ।)
Solution:
ଦର : ABCD ଟ୍ରାପିଚ୍ଚିଯମ୍6ର \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{DC}}\) , △ADO ~ △BCO |
ସ୍ତ।ମାଶ୍ୟ : AD = BC
ପାଣମ୍କ : \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{DC}}\)
⇒ △ABD ର ସେତ୍ରଫଳ – △ABC ର ସେତ୍ରଫଳ
⇒ △ABD ର ସେତ୍ରଫଳ – △AOB ର ସେତ୍ରଫଳ
= △ABC ର ସେତ୍ରଫଳ – △AOB ର ସେତ୍ରଫଳ
⇒ △ADO ର ସେତ୍ରଫଳ – △BOC ର ସେତ୍ରଫଳ |
ପ୍ନନଣ୍ଡ , △ADO ~ △BCO (ଜଉ)
⇒ △ADO ≅ △BCO
(∵ ଦୁଇଟି ସଦୃଶ ତ୍ରିଭୁଜ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ହେଲେ ସେ ଦୁଇଟି ସର୍ବସମ ହେବେ । )
⇒ AD = BC

Question 15.
△ABC ର \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{AC}}\) ବାହୁ ଉପରେ ଯଥାକ୍ରମେ X ଓ Y ବିନ୍ଦୁ ଅବସ୍ଥିତ ଯେପରିକି \(\overline{\mathrm{XY}}\) || \(\overline{\mathrm{BC}}\)ପ୍ରମାଣ କର ଯେ, △ABC ର ମଧ୍ୟମା \(\overline{\mathrm{AD}}\) , \(\overline{\mathrm{XY}}\) କୁ ସମତ୍ତିଖଣ୍ଡ କରେ ।
Solution:
ଦର : △ABC ର \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{AC}}\) ବାହୁ ଉପରେ ଯଥାକ୍ରମେ X ଓ Y ବିନ୍ଦୁ ଅବସ୍ଥିତ ଯେପରିକି \(\overline{\mathrm{XY}}\) || \(\overline{\mathrm{BC}}\) | \(\overline{\mathrm{AD}}\) ତ୍ରିରୁ ଜର ଏକ ମଧ୍ୟମା | \(\overline{\mathrm{AD}}\) ଓ \(\overline{\mathrm{XY}}\) ର ଛେଦ ଦିନ୍ଦ୍ର O |
ସ୍ତ।ମାଶ୍ୟ : OX = OY
ପାଣମ୍କ : △AXO ଓ △ABD ଦର

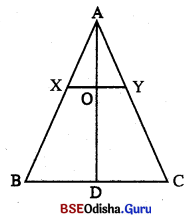
∠AXO ≅ ∠ABD (ର୍ଥନ୍ମରୁପ 6କାଣ) (∵ \(\overline{\mathrm{OX}}\) || \(\overline{\mathrm{BD}}\)
∠AOX ≅ ∠ADB (ର୍ଥନ୍ମରୁପ 6କାଣ) (∵ \(\overline{\mathrm{OX}}\) || \(\overline{\mathrm{BD}}\)
⇒ △AXO ≅ △ABD (6କା. 6କା. 6କା. ସାଦ୍ଶ୍ୟ)
⇒ \(\frac { AO }{ AD }\) = \(\frac { OX }{ DB }\) (ସାଦ୍ୱଶ୍ୟର ସଂଳା)
ସେଦିପରି △AYO ~ △ACD ⇒ \(\frac { AO }{ AD }\) = \(\frac { OY }{ DC }\)
⇒ \(\frac { OX }{ DB }\) = \(\frac { OY }{ DC }\) ⇒ OX = OY (∵DB = DC ଦଇ)

Question 16.
△ABC ରେ \(\overline{\mathrm{AD}}\) ଏକ ମଧ୍ୟମା ଏବଂ \(\overline{\mathrm{AD}}\) ର ମଧ୍ୟବିନ୍ଦୁ E | \(\overrightarrow{\mathbf{B E}}\) ରଶ୍ମି \(\overline{\mathrm{AC}}\) କୁ X ବିନ୍ଦୁରେ ଛେଦକଲେ, ପ୍ରମାଣ କର ଯେ BE = 3EX |
Solution:

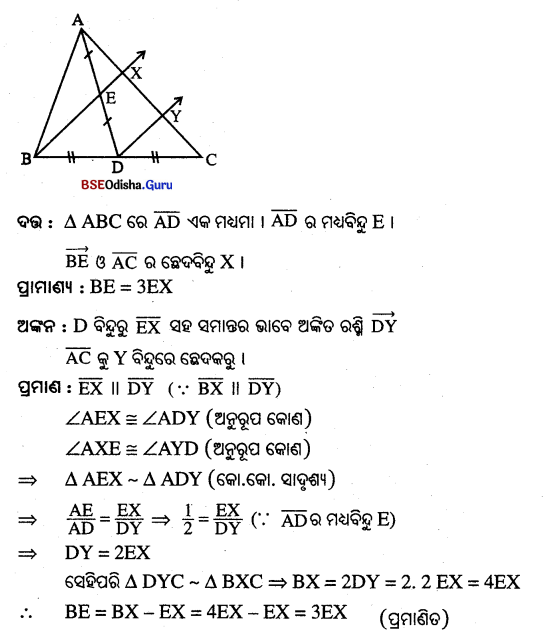
Question 17.
△ABC 6ର \(\overline{\mathrm{AD}}\) ⊥\(\overline{\mathrm{BC}}\) ଏବଂ AD² = BD. CD ହେଲେ, ପ୍ରମାଣକର ଯେ
(i) ∠BAC ଏକ ସମକୋଣ,
(ii) △ABD ର କ୍ଷେତ୍ରଫଳ ଓ △CADର କ୍ଷେତ୍ରଫଳ AB² ଓ AC² ସହ ସମାନୁପାତୀ
Solution:

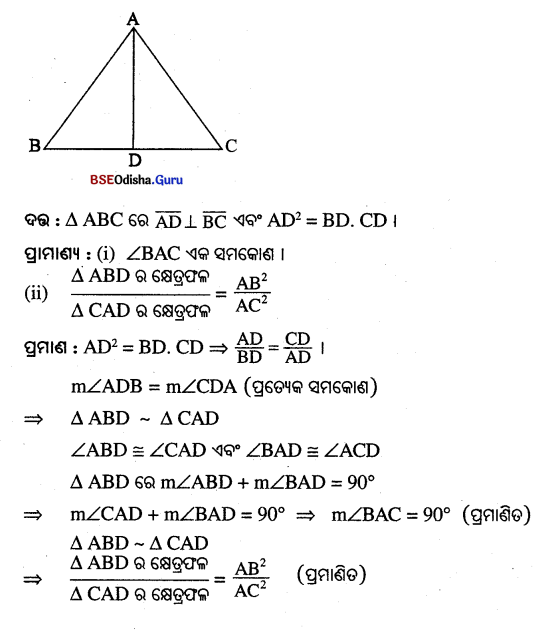
Question 18.
△ABC ଓ △DEF 6ର m∠A = m∠D, m∠B = m∠E | \(\overline{\mathrm{BC}}\) ଓ \(\overline{\mathrm{EF}}\) ଉ ମଧ୍ୟ ଦିନ୍ଦୁ ଯଥାକୁ ମେ X ଓ Y ହେଲେ , ପ୍ରମାଣ କର ଯେ
(i) △AXC ~ △DYF (ii) △AXB ~ △DYF |
Solution:

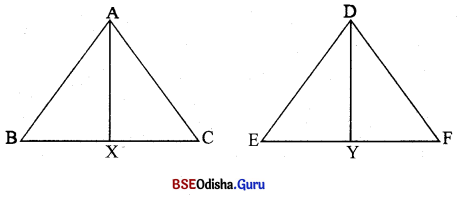
ସ୍ତ।ମାଶ୍ୟ : (i) △AXC ~ △DYF (ii) △AXB ~ △DYF
ପାଣମ୍କ : △ABC ଓ △DEF 6ର m∠A = m∠D, ଓ m∠B = m∠E
⇒ △ABC ~ △DEF (6କା. 6କା. 6କା. ସାଦ୍ଶ୍ୟ)
⇒ \(\frac { AB }{ DE }\) = \(\frac { BC }{ EF }\) = \(\frac { AC }{ DF }\)
⇒ \(\frac { AB }{ BC }\) = \(\frac { DE }{ EF }\) ⇒ \(\frac { AB }{ 2BX }\) = \(\frac { DE }{ 2EY }\) (∵ X, \(\overline{\mathrm{BC}}\) ର ମଧ୍ୟଦିନ୍ଦୁ ଓ Y, \(\overline{\mathrm{EY}}\) ରମଧ୍ୟଦିନ୍ଦୁ )
⇒ \(\frac { AB }{ BX }\) = \(\frac { DE }{ EY }\)
ର୍ଥତ୍ରଗତ ∠ABX ≅ △DEY (∵ m∠B = m∠E)
⇒ △AXB ~ △DYE
ସେହପରି ପ୍ରମାଣ କରାଯାଇପାରିବ △AXC ~ △DYE |

Question 19.
ପାଶ୍ୱମ୍ ଟି ତୃଭେ △ABC ର \(\overline{\mathrm{AB}}\) ଉପରିସ୍କ Q ଏକ ଦିନ୍ଦୁ , \(\overline{\mathrm{QR}}\) || \(\overline{\mathrm{BC}}\) 6ପପରିକି A-R-C, \(\overline{\mathrm{DR}}\) || \(\overline{\mathrm{QC}}\) ରମଧ୍ୟଦିନ୍ଦୁ A-D-B | ପ୍ରମାଣକର ମେ AQ² = AD × AB |

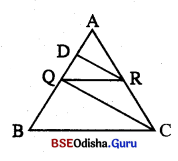
Solution:
ଦର : △ABC ର \(\overline{\mathrm{AB}}\) ଭପରିସ୍ଥ Q ଏକ ଦିନ୍ଦୁ , \(\overline{\mathrm{QR}}\) || \(\overline{\mathrm{BC}}\) 6ଯପରିକି
A-R-C ଏବଂ \(\overline{\mathrm{DR}}\) || \(\overline{\mathrm{QC}}\) 6ଯପରିକି A-D-B |
ସ୍ତ।ମାଶ୍ୟ : AQ² = AD × AB
ପାଣମ୍କ : △AQC ରେ \(\overline{\mathrm{DR}}\) || \(\overline{\mathrm{QC}}\)
⇒ \(\frac { AR }{ AC }\) = \(\frac { AD }{ AQ }\) …(i)
△ABC ରେ \(\overline{\mathrm{QR}}\) || \(\overline{\mathrm{BC}}\) ⇒ \(\frac { AR }{ AC }\) = \(\frac { AQ }{ AB }\) …(ii)
(i) ଓ (ii ) ହ \(\frac { AQ }{ AB }\) = \(\frac { AD }{ AQ }\) ⇒ AQ² = AD × AB

Question 20.
ପାଶଙ୍କ ଚିତ୍ର 6ର \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{EF}}\) ଏର୍ଦ \(\overline{\mathrm{AF}}\) ଓ
\(\overline{\mathrm{BE}}\) ପରସ୍ତରକୁ C ବିନ୍ଦୁ 6ର 6ଛଦ କରନ୍ତି | ପ୍ରମାଣ କର ସେ EF × BD = DF × AB |
Solution:

Question 21.
ଦୁଇଟି ସଦୃଶ ତ୍ରିଭୁଜର ଅନ୍ତଃବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ବୟର ଅନୁପାତ, ଉକ୍ତ ତ୍ରିଭୁଜର ଦୁଇଟି ଅନୁରୂପ ବାହୁର ଦୈର୍ଘ୍ୟର ଅନୁପାତ ସହ ସମାନ, ପ୍ରମାଣ କର ।
Solution:

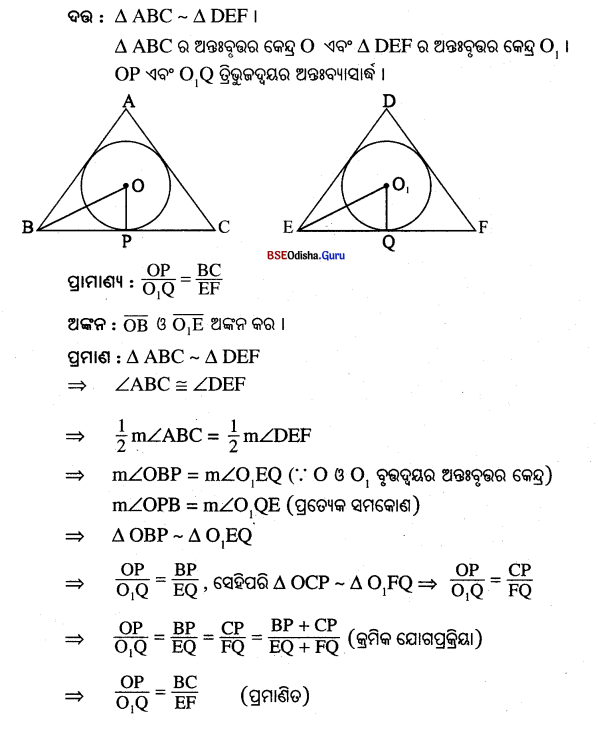
Question 22.
A-P-B ଓ A-Q-B 6ହାଲେ ଏଇ \(\frac { AP }{ PB }\) = \(\frac { AQ }{ QB }\) 6ହାଲେ , ପ୍ତମାଣା କର ମେ P ଓ Q ଥିରିନ୍ନ |
Solution:

Question 23.
ପାଣମ୍ଠ ଚିତ୍ରରେ △ABC ର ∠ABC ଏକ ଶୁକ6କାଣ | A ରୁ \(\overrightarrow{\mathbf{B C}}\) ପ୍ରତ ଅଳିତ ଲମୂର ପାଦ ଦିନ୍ଦୁ D | ଯଦି AD² = BD. DC ହୁଏ , ପ୍ରମାଣ କର ଯେ ∠BAD ଓ ∠CAD ପରମର ଅନୁତ୍ପରକ |

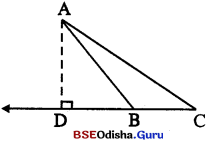
Solution:
ଦର : △ABC ରେ ∠ABC ତ୍ପଳ6କାଣ | \(\overline{\mathrm{AD}}\) ⊥ \(\overrightarrow{\mathbf{CB}}\) , AD² = BD. DC
ପ୍ରାମାଣ୍ୟ: m∠BAD + m∠CAD = 90°
ପ୍ରାମାଣ : AD² = BD. DC (ଦର)
⇒ \(\frac { AD }{ BD }\) = \(\frac { DC }{ AD }\)
ଅନ୍ତଗତ ∠ADB ≅ ∠ADC (ପ୍ତ6ତ୍ୟକ ସମ6ଳାଣ)
⇒ △ADB ~ △CDA
⇒ ∠BAD ≅ ∠ACD
△ADC ରେ m∠ACD + m∠CAD = 90°
⇒ m∠BAD + m∠CAD = 90° (∵ ∠BAD ≅ ∠ACD)

Question 24.
△ABC ର \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{AC}}\) ଉପରେ ଯଥାକ୍ରମେ X ଓ Y ବିନ୍ଦୁ ଅବସ୍ଥିତ, ଯେପରିକି \(\overline{\mathrm{XY}}\) || \(\overline{\mathrm{BC}}\) ଟ୍ରାପିଜିୟମ୍ XBCY ର କ୍ଷେତ୍ରଫଳ, △AXY ର କ୍ଷେତ୍ରଫଳର ଆଠଗୁଣ ହେଲେ, AX : BX ନିର୍ଣ୍ଣୟ କର ।
Solution:

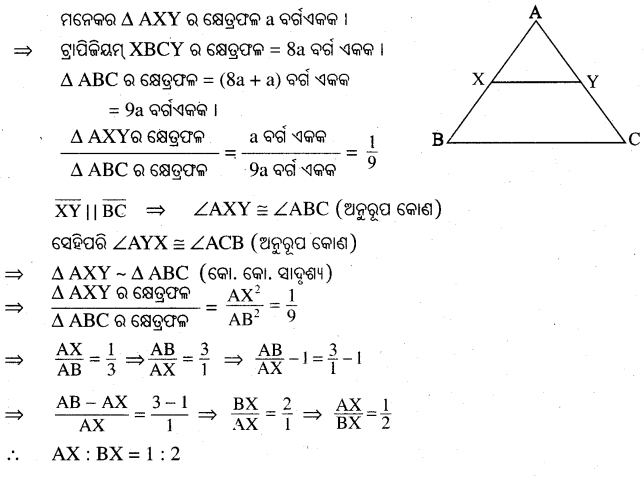
Question 25.
ABCD ଏକ ସ|ମାନ୍ତରିକ ଚିତ୍ର | \(\overrightarrow{\mathbf{AG}}\) ରଣ , \(\overline{\mathrm{BD}}\) , \(\overline{\mathrm{CD}}\) ଓ \(\overrightarrow{\mathbf{BC}}\) କୁ ଯଥାକ୍ତ6ମ E, F ଓ G ଦିନ୍ଦୁ 6ର 6ରଦରକା , ତ୍ପମାଣ କର ଯେ AE : EG = AF : AG |
Solution:

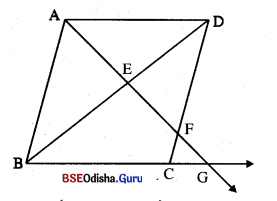
ଦର୍ : ABCD ଏକ ସ|ମାନ୍ତରିକ ଚିତ୍ର | \(\overrightarrow{\mathbf{AG}}\) ରଣ , \(\overline{\mathrm{BD}}\) , \(\overline{\mathrm{CD}}\) ଓ \(\overrightarrow{\mathbf{BC}}\) କୁ ଯଥାକ୍ତ6ମ E, F ଓ G ଦିନ୍ଦୁ 6ର 6ରଦରକା
ପ୍ରାମାଣ୍ୟ: AE : EG = AF : AG
ପ୍ରାମାଣ : △ABG ରେ \(\overline{\mathrm{CF}}\) || \(\overline{\mathrm{BA}}\) |
⇒ \(\frac { BC }{ BG }\) = \(\frac { AF }{ AG }\)
⇒ \(\frac { AF }{ AG }\) = \(\frac { BC }{ BG }\) = ⇒ \(\frac { AD }{ BG }\) (∵ AD = BC)
ପୁନଶ୍ଚ △AED ଓ △GEB ରେ ∠DAE ≅ ∠EGB (ଏଲାନ୍ତର ଲୋଣ)
∠AED ≅ ∠GEB (ପୃତାପ ଲୋଣ)
⇒ △AED ~ △GEB (କୋ . କୋ .ସାହଣ୍ୟ)
⇒ \(\frac { AD }{ BG }\) = \(\frac { AE }{ EG }\) (ସାଦୃଶ୍ୟର ସକା)
⇒ \(\frac { AE }{ EG }\) = \(\frac { AF }{ AG }\) (∵ \(\frac { AD }{ BG }\) = \(\frac { AF }{ AG }\))