CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Ex 14(d)

Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 14 Limit and Differentiation Ex 14(d) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Exercise 14(d)

Question 1.

Find the derivative of the following functions ‘an initio’, that is, using the definition.
(i) 2x³
Solution:

(ii) x⁴
Solution:

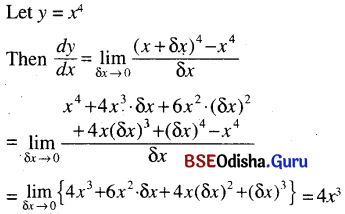
(iii) x² + 1
Solution:

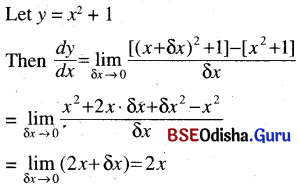
(iv) \(\frac{1}{x}\)
Solution:

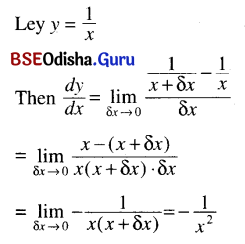
(v) \(\frac{1}{3 x+2}\)
Solution:

(vi) \(\frac{1}{x^2}\)
Solution:

(vii) \(\frac{x}{x+1}\)
Solution:

(viii) t(t – 1)
Solution:

(ix) s² – bs + 5
Solution:

(x) √x
Solution:

\(\frac{1}{\sqrt{z}+\sqrt{z}}=\frac{1}{2 \sqrt{z}}\)

(xi) tan θ
Solution:

(xii) cos 2θ
Solution:

(xiii) x sin x
Solution:

Question 2.
Find the derivative of the following function from the definition at the indicated points. Test whether the following functions are differentiable at the indicated points. If so find the derivative.
(i) x⁴ at x = 2
Solution:

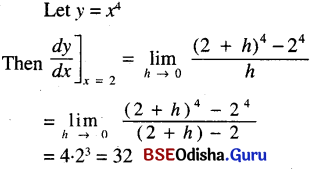
(ii) 2x² + x + 1 at x = 1
Solution:

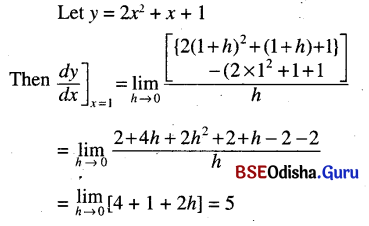
(iii) x³ + 2x² – 1 at x = 0
Solution:
Let x³ + 2x² – 1
Then \(\left.\frac{d y}{d x}\right]_{x=0}\) = \(\lim _{h \rightarrow 0}\left[\frac{\left(h^3+2 h^2-1\right)-(-1)}{h}\right]\)
= \(\lim _{h \rightarrow 0}\) (h² + 2h) = 0

(iv) tan x at x = \(\frac{\pi}{3}\)
Solution:

(v) \(\sqrt{3 x+2}\) at x = 0
Solution:

(vi) In x at x = 2
Solution:

(vii) \(e^x\) at x = 1
Solution:

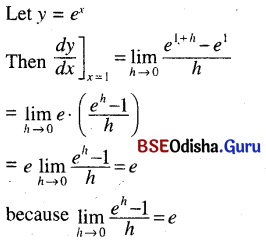
(viii) sin² θ at θ = \(\frac{\pi}{4}\)
Solution:

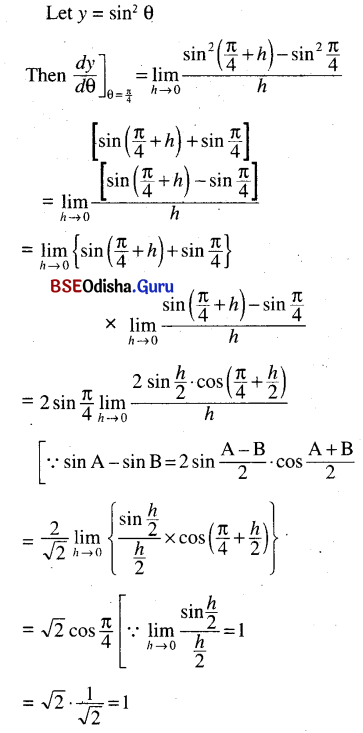
Question 3.
\(\frac{x+1}{x-1}\) at x = -1
Solution:
We know that a function f(x) is differentiable at a point
x = c if (i) L.H.D. exists
(ii) R.H.D. exists
(iii) L.H.D. = R.H.D
Let f(x) = \(\frac{x+1}{x-1}\)

Thus L.H.D. and R.H.D. both exist and L.H.D. = R.H.D.
Hence f(x) is differentiable at x = -1 and the derivative is –\(\frac{1}{2}\)

Question 4.
√x at x = 0
Solution:
Let f(x) = √x
Then f(0) = 0

Question 5.
f(x) = \(\left\{\begin{array}{r}
1-x, x \leq \frac{1}{2} \\
x, x>\frac{1}{2}
\end{array} \text { at } x=\frac{1}{2}\right.\)
Solution:

Question 6.
f(x) = \(\left\{\begin{array}{r}
\sin \frac{1}{x}, x \neq 0 \\
0, x=0
\end{array}\right.\) at x = 0
Solution:
f(0) = 0

Question 7.
f(x) = \(\left\{\begin{array}{r}
x^2 \sin \frac{1}{x^{\prime}}, x \neq 0 \\
0, x=0
\end{array}\right.\) at x = 0
Solution:
f(0) = 0