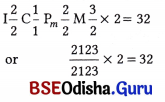Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 18 Body Fluids and Circulation Textbook Questions and Answers.
CHSE Odisha 11th Class Biology Chapter 18 Question Answer Body Fluids and Circulation
Body Fluids and Circulation Class 11 Questions and Answers CHSE Odisha
Very Short Answer Types Questions
Objective Type Questions
Question 1.
Double circulation is exhibited by
(a) Rohu
(b) Cockroach
(c) Scoliodon
(d) Frog
Answer:
(d) Frog
Question 2.
Which of the following is not a granulocyte?
(a) Neutrophil
(b) Monocyte
(c) Eosinophil
(d) Basophil
Answer:
(b) Monocyte
Question 3.
Serum does not contain
(a) fibrin
(b) albumin
(c) globulin
(d) bilirubin
Answer:
(a) fibrin
Question 4.
Drumstick, representing sex chromatin is present in
(a) eosinophil
(b) neutrophil
(c) lymphocyte
(d) monocyte
Answer:
(b) neutrophil
Question 5.
Adult haemoglobin (HbA) contains
(a) Gamma globin chains
(b) Beta globin chains
(c) Epsilon globin chains
(d) Zeta globin chains
Answer:
(b) Beta globin chains
Question 6.
An amino acid substitution in the beta globin chain causes
(a) Haemolytic anemia
(b) Pernicious anemia
(c) Microcytic anemia
(d) Sickle-cell anemia
Answer:
(b) Pernicious anemia
Question 7.
The presence of a large number of immature leucocytes in the circulation is indicative of
(a) leucocytosis
(b) leukemia
(c) leucopenia
(d) leucomorphosis
Answer:
(a) leucocytosis
Question 8.
Find the incorrect pair.
(a) Neutrophil – Phagocyte
(b) Eosinophil – Histamine
(c) Lymphocyte – Immunoglobulin
(d) Monocyte – Macrophage
Answer:
(b) Eosinophil – Histamine
Question 9.
Open circulation is exhibited by
(a) annelids
(b) vertebrates
(c) arthropods
(d) protectorates
Answer:
(c) arthropods
Question 10.
Myogenic heart is present in:
(a) annelids
(b) molluscs
(c) arthropods
(d) vertebrates
Answer:
(d) vertebrates
Question 11.
An instrument that measures the blood pressure is known as
(a) Haemometer
(b) Haemocytometer
(c) Sphygnomanometer
(d) Haemoglobinometer
Answer:
(c) Sphygnomanometer
Question 12.
Pacemaker is synonymous with
(a) SA Node
(b) Bundle of His
(c) AV Node
(d) Purkinje fibers
Answer:
(a) SA Node
Question 13.
Find out the correct route of blood circulation
(a) Venacava → Left atrium → Left ventricle → Pulmonary artery → Lung → Pulmonary vein → Right atrium → Right ventricle → Aorta
(b) Venacava → Right atrium → Right ventricle → Pulmonary artery → Lung → Pulmonary vein → Left atrium → Left ventricle → Aorta
(c) Venacava → Left atrium → Left ventricle → Pulmonary vein → Lung → Pulmonary artery → Right atrium → Right ventricle → Aorta
(d) Venacava → Left atrium → Right ventricle → Pulmonary artery → Lung → Pulmonary Vein → Left atrium → Right ventricle → Aorta
Answer:
(b) Venacava → Right atrium → Right ventricle → Pulmonary artery → Lung → Pulmonary vein → Left atrium → Left ventricle → Aorta
Question 14.
Find the incorrect match:
(a) Blood group A – Antigen A on red cell and anti-B antibody in the serum
(b) Blood group B – Antigen B on red cell and anti-A antibody in the serum
(c) Blood group AB – Antigen B on red cell and anti-A antibody in the serum
(d) Blood group O – No antigen A or B on the red cell and both anti-A and anti- B in the serum
Answer:
(c) Blood group AB – Antigen B on red cell and anti-A antibody in the serum
Question 15.
The fourth heart sound is produced by
(a) Closure of the aortic and pulmonary valves
(b) Closure of the bicuspid and tricuspid valves
(c) Vibration in the ventricular wall during systole
(d) Rapid ventricular filling
Answer:
(d) Rapid ventricular filling
Question 16.
Why of the following is not a part of the intrinsic blood coagulation pathway?
(a) Tissue thromboplastin
(b) Prothrombin
(c) Fibrinogen
(d) Ca2+
Answer:
(a) Tissue thromboplastin
Question 17.
Thalasemia is characterised by
(a) Globin chains are abnormal in haemoglobin
(b) The structure of heme is altered in haemoglobin
(c) Decreased synthesis of normal globin chains in haemoglobin
(d) Complete absence of globin chains in haemoglobin
Answer:
(c) Decreased synthesis of normal globin chains in haemoglobin
Question 18.
Complete (third degree) heart block is due to
(a) Ventricular fibrillation
(b) The conduct from the atria to the ventricles is completely interrupted
(c) The conduct from the atria to the ventricles is partially blocked or slowed
(d) One branch of the bundle of His is inhibited
Answer:
(a) Ventricular fibrillation
Answer the Following in One Word
Question 1.
The blood filled space and the blood in cockroach.
Answer:
Haemocoel and Haemolymph
Question 2.
The number of pulsatile chambers in the heart of cockroach.
Answer:
13
Question 3.
The heart of cyclostomes and fishes through which deoxygenated blood always circulates.
Answer:
Venous heart
Question 4.
The percentage of erythrocytes in the total volume of human blood.
Answer:
45%
Question 5.
Swelling and disintegration of erythrocytes in a hypotonic solution.
Answer:
Haemolysis
Question 6.
Shrinking of erythrocytes in a hypertonic solution.
Answer:
Crenation
Question 7.
Iron is transported in conjugation with a protein carrier in the blood.
Answer:
Transferrin
Question 8.
Higher number of erythrocytes than normal in the blood.
Answer:
Polycythemia
Question 9.
Abnormally lower haemoglobin percentage in the blood.
Answer:
Anemia
Question 10.
Lack of ankyrin in the cytoskeleton of erythrocytes causes a hereditary disorder.
Answer:
Spherocytosis
Question 11.
An amino acid substitution in the p-globin chain of the haemoglobin causes a hereditary disorder
Answer:
Sickle- cell anemia
Question 12.
Expression of abnormal polypeptides in the haemoglobin by mutant genes gives rise to a pathological condition.
Answer:
Haemoglobinopathies
Question 13.
Decreased synthesis of normal a and P globin chain gives rise to a pathological condition.
Answer:
Thalasemia
Question 14.
Trans membrane migration of leucocytes into the tissues from the blood vessels.
Answer:
Diapedesis
Question 15.
The site of maturation of lymphocytes into B-lymphocytes takes place in an organ of bird.
Answer:
Thymus
Question 16.
An enzyme from the damaged tissue that activates prothrombin into thrombin.
Answer:
Protease
Question 17.
An abnormally higher number of thrombocytes in the blood.
Answer:
Thrombocytosis
Question 18.
An abnormally lower number of thrombocytes in the blood.
Answer:
Thrombocytopenia
Question 19.
The process of formation of erythrocytes in the bone marrow.
Answer:
Erythropoiesis
Question 20.
The cytokine, thrombopoietin stimulates a large multinucleate cell to from a large number of platelets.
Answer:
Megakaryocytes
Question 21.
The inter atrial connection in the embryonic heart of human.
Answer:
Foramen ovale
Question 22.
The footprint of embryonic inter-atrial connection in the inter-atrial septum of adult.
Answer:
Fossa ovalis
Question 23.
A vascular connection between the pulmonary trunk and the aorta in the embryonic heart of human.
Answer:
Ductus arteriosus
Question 24.
The outer squamous epithelium layer of the heart.
Answer:
Pericardium
Question 25.
The innermost squamous epithelium layer of the heart.
Answer:
Endocardium
Question 26.
The tendionous threads attaching the atrio -ventricular valves with the papillary muscles.
Answer:
Chordae tendineae
Question 27.
The blood pressure is measured by an instrument.
Answer:
Sphygmomanometer
Question 28.
The sound detected by the stethoscope in measuring the blood pressure.
Answer:
Sound of korotkoff
Question 29.
A protein that activates inactive plasminogen into active plasmin.
Answer:
Kallikrenin
Question 30.
The clinical condition, in which the conceived Rh+ antibody preparation injected into the Rh– mothe dies.
Answer:
Erythroblastosis fetalis
Question 31.
The trade name of the anti Rh antibody preparation injected into the Rh– mother.
Answer:
RhoGAM
Question 32.
The hardening and constriction of large and medium sized arteries due to the deposition of metabolic byproducts on the endothelium.
Answer:
Arteriosclerosis
Question 33.
The constriction of the lumen of large and medium sized arteries due to deposition of lipids or their derivatives on the endothelium.
Answer:
Artherosclerosis
Question 34.
The unbearable pain in the heart due to formation of an excess of lactate in the cardiac muscle due to prologed ischemia (lack of oxygen).
Answer:
Angina pectoris
Question 35.
An irreversible injury followed by death to the myocardial cells due to prolonged ischemia.
Answer:
Myocardial infarction
Question 36.
The drug that prevents atherosclerosis by inhibiting an enzyme in the cholesterol biosynthetic pathway in the liver.
Answer:
Statins
Question 37.
The radiograph that detects blockages in the coronary artery.
Answer:
Angiogram
Question 38.
The technique of clearing the blockages in the coronary artery.
Answer:
Angioplasty
Question 39.
A cylindrical support attached to the artery to prevent its narrowing down subsequently.
Answer:
Stent
Question 40.
Abnormal patterns of electrical conduction in the heart causes abnormal beating.
Answer:
Arrhythmias
Question 40.
A cardiac rate slower than 60 beats/min.
Answer:
Bradycardia
Question 41.
A cardiac rate faster than 100 beats/ min.
Answer:
Tachycardia
Question 42.
The coordinate contraction of myocardial cells at a rate of 200-300/ min.
Answer:
Systole
Question 43.
The contraction of different groups of myocardial cells at different times.
Answer:
Diastole
Question 44.
Ventricular fibrillation leads to complete cessation of blood supply to the brain and hence it’s functioning.
Answer:
Stroke
Fill in the Blanks
Question 1.
Blood circulation in human was discovered by …………….. .
Answer:
William Harvey
Question 2.
There are 13 pulsatile chambers in the heart of cockroach. Each chamber opens by apertures, known as …………….. .
Answer:
Sinuses
Question 3.
Two perforated diaphragms divide the haemocoel of cockroach into three sinuses, namely and …………….. , …………….. and …………….. .
Answer:
pericardial, perivisceral and perineural
Question 4.
………….. muscles, attached to the dorsal diaphragm regulate the contraction and relaxation of the heart in cockroach.
Answer:
Muscles
Question 5.
In double circulation, there are two circuits. One is pulmonary and the other is ………….. .
Answer:
Systemic
Question 6.
The average longevity of human erythrocytes is ………….. days.
Answer:
120
Question 7.
Human erythrocytes, often, pile up on their lateral sides forming a ………….. .
Answer:
rouleaux
Question 8.
The respiratory pigment in human blood is known as ………….. .
Answer:
haemoglobin
Question 9.
Haemoglobin is a conjugate protein consisting of a protein part ……….. conjugated to a non-protein part ………….. .
Answer:
Globin, haeme
Question 10.
In fetal haemoglobin (HbF), the beta- globin chains are substituted by ………….. globin chains.
Answer:
gamma
Question 11.
Deficiency of vitamin-B12 causes ………….. anemia.
Answer:
Pernicious
Question 12.
Small size of erythrocytes and hence reduced haemoglobin content causes ………….. anemia.
Answer:
microcytic
Question 13.
Excessive destruction of erythrocytes causes ………….. anemia.
Answer:
aplastic
Question 14.
Four oxygen molecules bind to a molecule of haemoglobin one after another forming oxyhaemoglobin. This type of binding is known as cooperative or ………….. binding.
Answer:
allosteric
Question 15.
Erythropoiesis is stimulated by a hormone called ………….. which is secreted by ………….. .
Answer:
Erythropoietin , kidney
Question 16.
Increases in the number of leucocytes above normal is known as ………….. .
Answer:
leucocytosis
Question 17.
Decrease in the number of leucocytes below normal is known as ………….. .
Answer:
leucopenia
Question 18.
Neutrophils turn into ………….. at the site of microbial infection.
Answer:
phagocytes
Question 19.
Infection by helminth larvae causes a proliferation of a class of leucocytes, called ………….. .
Answer:
lymphocytes
Question 20.
………….. and mast cells release at the site of infection, which causes inflammation.
Answer:
Basophil, histamine
Question 21.
………….. infilter through the wall of the blood vessels into the tissues and turn into macrophages.
Answer:
Monocytes
Question 22.
The heart is surrounded by a double-walled membrane, known as ………….. .
Answer:
pericardium
Question 23.
External furrows, marking the internal divisions of the heart are known as ………….. .
Answer:
sulci
Question 24.
The wall of the heart consists of three layers, such as epicardium, myocardium and …………..
Answer:
endocardium
Question 25.
The venacava open into ………….. of the heart.
Answer:
right atrium
Question 26.
Semilunar valves guard the openings of ………….. and ………….. trunks.
Answer:
Aorta, pulmonary
Question 27.
Haemolysis of red cells results in the formation of ruptured plasma, membranes, known as ………….. .
Answer:
red cell ghosts
Question 28.
Crenation results in the formation of shrunken erythrocytes called ………….. .
Answer:
echinocytes
Question 29.
The left atrio- ventricular aperture is guarded by a ………….. or ………….. valve.
Answer:
bicuspid, mitral
Question 30.
Muscular bundles, projecting into the cavities of the ventricles constitute ………….. .
Answer:
papillary muscles
Question 31.
The heart itself is supplied by ………….. arteries.
Answer:
Coronary artery
Question 32.
Persons with ………….. are treated with digitalis.
Answer:
heart attack
Question 33.
Numerical expression of normal blood pressure of human is ………….. .
Answer:
120/80 mm Hg
Question 34.
………….. discovered the ABO blood grouping system.
Answer:
Karl Landsteiner
Question 35.
The AB blood group was discovered by ………….. and ………….. .
Answer:
Sturli, Decastallo
Question 36.
The Rh blood grouping was discovered by ………….. .
Answer:
Alexander S Wiener
Question 37.
Persons with ………….. blood group are known as universal donors.
Answer:
O
Question 38.
Persons with ………….. blood group are known as universal recipients.
Answer:
AB
Question 39.
The process of forming a clot in the wall of a damaged blood vessel and preventing blood loss is known as ………….. .
Answer:
blood clotting
Question 40.
The endothelial cells secrete ………….. and ………….. which act as vasodilators and inhibit platelet aggregation.
Answer:
Nitric oxide, Prostacyclin
Question 41.
The intrinsic pathway of blood clotting is initiated by the exposure of the plasma to negatively charged ………….. at the site of blood vessel damage.
Answer:
collagen
Question 42.
Extrinsic pathway of blood coagulation is initated by the releases of a tissue enzyme, at ………….. the site of tissue damage.
Answer:
Thromboplastin
Question 43.
The enzyme ………….. lyses fibrin mesh.
Answer:
plasmin
Question 44.
Streptokinase, a bacterial enzyme activates ………….. into ………….. .
Answer:
plasminogen , plasmin
Question 45.
Heparin, an anticoagulant activates ………….. .
Answer:
allergic reaction
Question 46.
Haemophilia A, an X- Linked recessive disorder, is caused due to the deficiency of a sub- unit of the blood coagulation factor ………….. the deficiency in another sub-unit of the same factor cause ………….. disease.
Answer:
Vm, von willebrand
Question 47.
Deficiency in the blood coagulation factor IX causes the disease ………….. .
Answer:
haemophilia B
Question 48.
Defective low density lipoprotein (LDL) receptors on the hepatocyte surface cause an inherited disease, known as ………….. .
Answer:
Artherosclerosis
Matching Type Questions
Question 1.
Match the following
| Group A |
Group B |
| 1. Venacava and coronary sinus |
(a) Left atrio-ventricular aperture |
| 2. Aortic trunk |
(b) Right atrium |
| 3. Pulmonary veins |
(c) Left ventricle |
| 4. Pulmonary trunk |
(d) Right atrio-ventricular aperture |
| 5. Tricuspid valve |
(e) Right ventricle |
| 6. Bicuspid (Mitral) valve |
(f) Left atrium |
Answer:
| Group A |
Group B |
| 1. Venacava and coronary sinus |
(b) Right atrium |
| 2. Aortic trunk |
(c) Left ventricle |
| 3. Pulmonary veins |
(f) Left atrium |
| 4. Pulmonary trunk |
(e) Right ventricle |
| 5. Tricuspid valve |
(d) Right atrio-ventricular aperture |
| 6. Bicuspid (Mitral) valve |
(a) Left atrio-ventricular aperture |
Question 2.
Match the following
| Group A |
Group B |
| 1. End diastolic volume |
(a) The volume of blood that remains in the ventricles following ventricular systole. |
| 2. Isovolumetric contraction |
(b) the volume of blood ejected following ventricular systole. |
| 3. Stroke volume |
(c) The ventricles relax as closed cavities. |
| 4. End systolic volume |
(d) The ventricles contract as closed cavities |
| 5. Isovolumetric relaxation |
(e) The volume of blood in the ventricles at the end of ventricular diastole. |
Answer:
| Group A |
Group B |
| 1. End diastolic volume |
(e) The volume of blood in the ventricles at the end of ventricular diastole. |
| 2. Isovolumetric contraction |
(d) The ventricles contract as closed cavities |
| 3. Stroke volume |
(b) the volume of blood ejected following ventricular systole. |
| 4. End systolic volume |
(a) The volume of blood that remains in the ventricles following ventricular systole. |
| 5. Isovolumetric relaxation |
(c) The ventricles relax as closed cavities. |
Question 3.
Match the following
| Group A |
Group B |
| 1. Baroreceptor reflex |
(a) Excretion of more water and sodium |
| 2. Antidiuretic hormone |
(b) Atrial wall |
| 3. Atrial stretch reflex |
(c) Regulates blood pressure by vasoconstriction |
| 4. Aldosterone |
(d) Aortic arch and carotid sinus |
| 5. Renin- Angiotensin |
(e) Reabsorption of salt and water by the kidneys |
| 6. Atrial Natriuretic peptide |
(f) Reabsorption of water by the kidneys. |
Answer:
| Group A |
Group B |
| 1. Baroreceptor reflex |
(d) Aortic arch and carotid sinus |
| 2. Antidiuretic hormone |
(f) Reabsorption of water by the kidneys. |
| 3. Atrial stretch reflex |
(b) Atrial wall |
| 4. Aldosterone |
(e) Reabsorption of salt and water by the kidneys |
| 5. Renin- Angiotensin |
(a) Excretion of more water and sodium |
| 6. Atrial Natriuretic peptide |
(c) Regulates blood pressure by vasoconstriction |
Short Answer Type Questions
Question 1.
Explain about the transport function of blood.
Answer:
Blood transports nutrients from alimentary canal to all the cells and tissue. This help in proper functioning and metabolic activities of body’s organs. Blood also transports respiratory gases such as O2 and CO2 from outside to the body and vice versa. It also helps in collection of excretory wastes from all parts of the body to the site of their elimination from the body.
Question 2.
What is open circulation ? Give an example.
Answer:
An open circulatory system is where the blood and interstitial fluid are allowed to mix in an organism.
Such organism don’t have true blood and the circulating fluid is referred to as haemolymph.
Organism with open circulatory system are arthropods and molluscs.
Question 3.
Why is the heart of cyclostomes and fishes called venous heart?
Answer:
The heart of cyclostomes and fishes is two chambered consisting an atria and a ventricle. Deoxygenated blood circulates through veins to gills for oxygenation and transported to all parts except heart. It is again collected by veins and emptied into the heart. The heart, thus contains only deoxygenated blood and known as venous heart.
Question 4.
What is systemic circulation?
Answer:
Systemic Circulation In this system, the pure blood is supplied to all parts of the body. During transport, the oxygenated (pure) blood entering the aorta is carried by a network of arteries, arterioles and capillaries to the tissues from where the deoxygenated (impure) blood is collected by a system of venules, veins and vena cava, thus, emptying it into the right atrium.
Question 5.
What is hematocrit?
Answer:
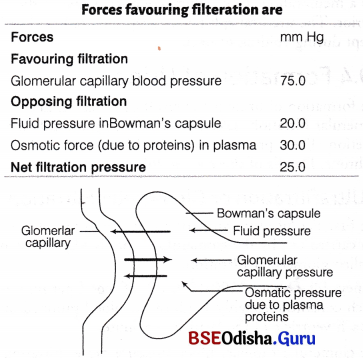
Haematocrit is the ratio of the volume of red blood cells to the total volume of blood. The erythrocytes constitutes approx 45% in men and 42% (women) to the total blood volume.
Question 6.
Why is the colour of the plasma straw yellow?
Answer:
It is a straw coloured, viscous, slightly alkaline aqueous body fluid. It forms about 55% of the blood. It’s straw colour is due to the presence of bilirubin and carotene.
Question 7.
What is a rouleauax? Where it is found?
Answer:
The rouleaux is the stacking of red blood cells one above the other when they are suspended in a suitable medium. It is seen when ESR is increased and plasma protein concentration is increased. It is caused by an increase in cathodal proteins like immunoglobulins and fibrinogen. The flat surface of the discoid RBCs give them a large surface area to make contact and stick with each other, thus forming a rouleauax.
Question 8.
What do you mean by haemolysis ?
Answer:
Haemolysis is the breakdown or destruction of red blood cells releasing the oxygen carrying pigment haemoglobin, into the surrounding medium. It is also a means of removing mature and dead RBCs from the bloodstream.
Question 9.
What is an echinocyte ?
Answer:
Echinocyte is a reversible condition of red blood cells. It is a form of RBC which has an abnormal cell membrane characterised by many small, evenly spaced thorny projections. It is seen when erythrocytes are placed in a hypertonic solution which leads to cell shrinkage. The phenomenon is called crenation and shrunken erythrocytes are called echinocytes.
Question 10.
What is haemoglobin A ?
Answer:
Haemoglobin A is called adult haemoglobin. It is made up of two β chains and two pairs of a chains (α2β2). Its the most common normal adult haemogloben (HbA); comprising over 97% of total RBC haemoglobin.
Question 11.
What is fetal haemoglobin?
Answer:
Fetal haemoglobin is the major haemoglobin present during gestation. It is completely replaced by adult haemoglobin by approx 6-12 months of age.
In fetal hb, the β globin chains are substituted by gamma(γ) chains. It has very high affinity towards oxygen and is more efficient than adult haemoglobin.
Question 12.
Explain about allosteric binding of oxygen to haemoglobin.
Answer:
Haemoglobin:
Haemoglobin is a conjugate protein consisting of a protein part globin conjugated to a non-protein part called haeme.
The globin consists of a and b polypeptides, two each.
The heme consist of four sub-units, each containing a porphyrin or tetra-pyrrole ring. At the centre of porphyrin, Fez+ is present which impart red colour to haemoglobin.
The Fe2+ is attached by four coordinate bonds to the four pyrrole rings and by two more coordinate bonds to the globin (α or β) chain. One of the coordinate bonds, by which it is attached to the globin chain is displaced by molecular oxygen and consequently, oxyhaemoglobin is formed. Due to its oxygen carrying function haemoglobin is known as a respiratory pigment. The haemoglobin containing two each of a and b globin chains is termed as adult haemoglobin (haemoglobin A).
The b globin chain in 25% of adult haemoglobin is substituted by d globin chain. In foetus, however, the b globin chains are substituted by g chains. This haemoglobin has been referred to as fetal haemoglobin (haemoglobin F).
Question 13.
What is sickle cell anemia? How does it differ from haemolytic anemia?
Answer:
Sickle Cell Anemia: The haemoglobin is abnormal due to an amino acid substitution in the b-globin chain. The erythrocytes remain sickle-shaped and the haemoglobin has a reduced oxygen carrying capacity. It is an autosomal recessive disorder.
Question 14.
Explain about leucopenia.
Answer:
The normal count of white blood cells is 5000-10,000 per cubic millimeter. When this count drops below 3500 per cubic millimeter in the blood indicates leucopenia.
The decrease in the number of leucocytes below the normal count is called leucopenia.
Question 15.
What is thalasemia ?
Answer:
Thalassemia: An autosomal recessive disease, occurring due to mutation or deletion of genes. Polypeptides are normal, there is decreased synthesis of α or β-globin accordingly the disorder is either α-thalassemia or β-thalasemia.
Question 16.
What is diapedesis?
Answer:
These are known to be the most active and motile constituent of blood as well as lymph. They do not possess the red colour pigment (haemoglobin) in them, so they are colourless in nature.
These are nucleated and are generally short lived cells. The number of WBCs are relatively lesser in number, about 6000-8000 mm³ of blood. They move in an amoeboid fashion.
These can squeeze through capillary wall and move to the site of action. This phenomenon is called diapedesis.
Question 17.
A basophil is functionally related to an areolar connective tissue cell. Name the cell and explain the function.
Answer:
Basophils are functionally related to mast cells. Mast cells are areolar tissues which releases granules and chemicals histamine, cytokinin, heparin and many proteases in the surrounding environment. They are chemical mediators causing inflammatory and allergic reactions.
Question 18.
Ennumerate the types of granulocytes and their individual functions.
Answer:
Agranulocytes They lack granules in their cytoplasm and have rounded or oval nucleus. Agranulocytes are also further subdivided into two main types
1. Lymphocytes These are smaller in size and have rounded indented nucleus. Lymphocytes are of further two types, i.e. B-cells and T-cells. Both of these (i.e. B and T-cells) are responsible for immune responses of the body.
2. Monocytes These are largest of all types of WBCs, but are fewer in number. Their nucleus is horse-shoe shaped. Mature monocytes are known as macrophages. They help to kill foreign particles. These are phagocytic in nature.
Img 1
Question 19.
Mention the two major functions of lymphocytes.
Answer:
Lymhyphocytes play an important role in the immune response generated by the body.
- The T-lymphocytes acts as killer cells which help in elimination of pathogenic microorganisms entering the host body.
- B-Cells / lymphocytes secretes antibody and memory cells.
Question 20.
What is hematopoiesis? Where does it occur?
Answer:
Haematopoises or haemopoiesis is the process of formation of blood cells. This process occurs in liver of the foetus when undifferentiated stem cells migrate from yolk sac to liver. After birth, liver stop the function of haematopoietic organ and bone marrow take up this function till death.
Question 21.
Why the human heart is myogenic?
Answer:
Myogenic Heart: In myogenic heart nerve stimulation is not required to initiate heartbeat and few localised cardiac muscles perform this function intrinsically. Node is the collection of specialised cardiac muscle cells, e.g. sino-atrial node (SA).
Question 22.
What is fossa ovalis ?
Answer:
The two atrium of human heart are separated from each other by a complete partition called the inter-atrial septum. Fossa ovalis is an oval shaped depression present just above the inferior vena cava orifice in intra-atrial septum in right atrium.
Question 23.
Why are atrio-ventricular valves called cuspid valves?
Answer:
The atrio ventricular valves i.e the mitral and tricuspid valves are present (bicuspid) between the upper chambers (atria) and lower chambers (ventricles).
These are so named because of the cusps or leaflet-like covering (three on tricuspid and two on bicuspid) on them.
Question 24.
What do you mean by action potential?
Answer:
The action potential is a transient depolarisation of the membranes of specialised myo cardial cells present in the S.A node.
Question 25.
For a moment (0.4 sec), the entire heart is in diastole-explain.
Answer:
The diastole (phase of relaxation) of the atria and ventricles always partly overlaps. Hence, both the atrial and ventricle chambers Eire in a diastole together for period of 0.4 seconds.
Question 26.
What do lubb and dupp signify?
Answer:
- LuBB: It is the first sound, being produced when inter auriculoventricular valves (tricuspid and bicuspid valve) are closed. This marks the end of the atrial systole and beginning of ventricular systole.
- DuPP: It is the second sound being produced when semilunar valves (of aorta and pulmonary artery) get closed. This marks the end of ventricular systole.
Question 27.
The standard notation of blood pressure (120/ 80 mm Hg) refer to systolic and diastolic pressures of the systemic circulation-Explain.
Answer:
The pressure exerted by the blood on the walls of blood vessels is called as blood pressure, Systolic blood pressure (contraction of ventricles) measures the pressure exerted on the artery wall during heart beats. This pressure rises to about 120 mm Hg.
Dieistolic blood pressure (ventricles relax and pressure in left ventricle falls below that of aorta) measures the pressure exerted by blood against artery walls when the heart is relaxing between beats. This pressure is measured to be 80 mm Hg. 120/80 mm Hg thus indicates the blood pressure of normal healthy individual.
Question 28.
How do antidiuretic hormone (ADH) regulate blood pressure?
Answer:
ADH or vassopressin is secreted by hypothalamus when there is excessive loss of fluid from the body or blood pressure is too low.
Osmotic sensors in the hypothalamus reacts to concentration of certain molecules like Na+,K+ Cl– and CO2. When their concentration is not balanced or blood pressure is too low, ADH is released. It has constrictory effect on blood vessels and thus increases the pressure by increasing the volume of water and blood in the body.
Question 29.
What is aldosterone? How it is related to the maintenance of blood pressure.
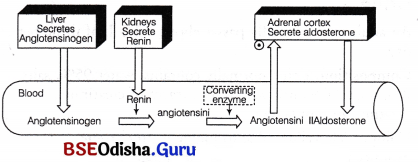
Answer:
Aldosterone is secreted by zona glomerulosa of adrenal gland which regulates water and electrolyte balance in the body.
If a decreased blood pressure is detected, the adrenal gland stimulates the stretch receptors to release aldosterone which inturn increases sodium reabsorption from the urine, sweat and the gut. This leads to increaseds molarity in the extracellular fluid which returnes the blood pressure towards normal.
Question 30.
What is ECG?
Answer:
ECG (Electrocardiogram) is a record of the electrical activity of heart. It shows the heart’s activity as line tracings on paper where the fluctuations; appearing are called waves.
An ECG graph includes deflections, i.e. P wave (atrial repolarisation) QRS wave (ventricular depolEirisation) and T wave (ventricular repolarization). Any deviation from normal ECG indicates abnormal functioning of heart.
Question 31.
What happens if there is a mismatched blood transfusion?
Answer:
It is always necessary to match the blood types prior to blood transfusion of both the donor and the recipient. If the types do not match a severe haemolytic reaction can occur in the recipient. This involves the the clumping or agglutination of blood cells and the red blood cells will be destroyed by recipients immune system.
Question 32.
What is haemolytic disease of the newborn ?
Answer:
This could be fatal to the developing foetus and could cause severe anaemia and jaundice to the developing baby. This is known as erythroblastosis foetalis or haemolytic disease of newborn.
Question 33.
What is platelet plug?
Answer:
When ever an injury occurs, the platelets come and stick together to the damaged endothelium forming a platelet plug. It temporarily seals the break in the vessel wall and blood clot formation occurs at the site.
Question 34.
What is platelet release reaction.?
Answer:
Plateletes forms a clot at the injury site. They release factors to stimulate further reactions. Plateletes adheres to collagen fibres in vessel wall by becoming adhesive and filamentous due to von willebrand factor. They degranulate releasing ADP, serotonin and throm boxane. This phenomenon is known as the platelet release reaction.
Question 35.
What is the function of streptokinase?
Answer:
Stretptokinase is a bacterial enzyme isolated from genetically modified Streptococcus.
It is used as clot buster for removing clots from the blood vessels of heart patients suffering from myocardial infarction. Streptokinase vaccinates plasminogen forming, plasmin.
Question 36.
What is EDTA? How does it help in blood preservation?
Answer:
EDTA is Ethylene Diamine tetra acetic Acid.
It is a chelating agent that binds calcium and other metals and also used as an anticoagulant for preserving blood samples.
It is added to sample collection tubes and bags to prevent blood cells from clumping and clotting together.
Question 37.
How does heparin act as an anticoagulant?
Answer:
Heparin is a natural anticoagulant. Inside an intact blood vessel the blood does not coagulate because of the presence of active anticoagulants like heparin.
It also activates antithrombin III a circulating plasma protein, which inactivates thrombin and other clotting factors.
Question 38.
What is arteriosclerosis?
Answer:
It is the hardening of arteries and arterioles due to the thickening of the fibres tissue and the consequent loss of elasticity. This mainly affects the vessels, which are mainly responsible for supplying blood to the heart muscle. It seems to occur due to deposition of calcium, fat cholesterol and fibrous tissues making the lumen of arteries narrower.
Img 2
(a) An artherosclerosis plaque in the arterial wall
(b) Cross seaction of a coronary artery showing an Artherosclerotic plaque and clot in lumen
512
Question 39.
What is the role of cholesterol in producing atherosclerosis?
Answer:
The cholesterol molecules conjugate with plasma proteins and articulate in blood as lipopoteins. They associate with endothelial cells triggering the synthesis of cell adhesion bimolecules specific for monocytes. The monocytes transforms into macrophages, engulfs the associated lipid and become foam cells. These together with more leucocytes form atherosclerotic plaques thus initiating the disease as the deposited lipids and macrophages calcifies.
Thus, the occurrence of atherosclerosis coincides with concentration of LDL (Low density lipoprotein) in blood.
Question 40.
What is angioplasty?
Answer:
Angioplasty is a procedure which involves opening of narrowed or blocked blood vessels (coronary arteries) that supply blood to the heart.
It restores normal blood to the heart by threading a catheter via a small puncture in arm or leg artery to the heart. Blocked artery opens when a tiny ballon is inflated in the catheter.
Question 41.
How does TPA help in dissolving a thrombus?
Answer:
TPA, tissue Plasminogen Activator is a protein found on endothelial cells involved in the breakdown of blood clots. It activates plasminogen to plasmin during clot formation. Human TPA is now a days also produced by recombinant- DNA technology.
Question 42.
What is bradycardia?
Answer:
Bradycardia is the term indicating a slow heart or pulse rate, i.e. under 50 beats/ minute. It also indicates a problem in heart’s electrical system.
Question 43.
What is lymph? How does it circulate?
Answer:
Lymph is a colourless fluid connective tissue with high concentration of specialised lymphocytes (WBC), floating in lymph vessels.
It circulates via an elaborate network of lymphatic vessels, which collects interstitial fluid along with some proteins and drains it back to major veins.
Write Brief Notes
Question 1.
Functions of blood
Answer:
Functions of blood Blood performs the following important functions .
- Helps in transportation of respiratory gases (i.e., O2, CO2, etc).
- Helps in healing of wounds.
- Maintains body pH, water and ionic balance.
- Fight against infections by forming body immunity.
- Also helps in transportation of hormones from endocrine glands to target organs.
Question 2.
Agranulocytes
Answer:
Agranulocytes They lack granules in their cytoplasm and have rounded or oval nucleus. Agranulocytes are also further subdivided into two main types
(a) Lymphocytes These are smaller in size and have rounded indented nucleus. Lymphocytes are of further two types, i.e. B-cells and T-cells. Both of these (i.e. B and T-cells) are responsible for immune responses of the body.
(b) Monocytes These are largest of all types of WBCs, but are fewer in number. Their nucleus is horse-shoe shaped. Mature monocytes are known as macrophages. They help to kill foreign particles. These are phagocytic in nature.
Img 1
Structure of agranulocytes, (a) Lymhyphocyts; and (b) Monocytes
Question 3.
Double circulation
Answer:
Double Circulation
The mammalian heart is four-chambered, undergoing the process of complete separate double circulation. This means that blood passes twice through the heart to supply the blood for once to the body. This transmission is necccssary, as it helps in oxygenation of blood.
The following processes constitute the double circulation
(i) Pulmonary Circulation In this system, blood completes its circulation from right ventricle to the left atria through the lungs. Here, the deoxygenated blood pumped by the right ventricle enters the pulmonary artery while, the left ventricle pumps blood into the aorta.
The deoxygenated blood is passed on to the lungs from where, the oxygenated blood is carried out by the pulmonary veins into the left atrium of heart.
(ii) Systemic Circulation In this system, the pure blood is supplied to all parts of the body. During transport, the oxygenated (pure) blood entering the aorta is carried by a network of arteries, arterioles and capillaries to the tissues from where the deoxygenated (impure) blood is collected by a system of venules, veins and vena cava, thus, emptying it into the right atrium.
This system provides essential nutrients, O2 and other essential substances to all the tissues of body and eventually takes away CO2 and other harmful substances away from tissues for their elimination from body.
Img 2
Plan of double circulation in a vertebrate
Question 4.
Haemoglobin
Answer:
Haemoglobin
Haemoglobin is a conjugate protein consisting of a protein part globin conjugated to a non-protein part called haeme.
The globin consists of a and b polypeptides, two each.
The heme consist of four sub-units, each containing a porphyrin or tetra-pyrrole ring. At the centre of porphyrin, Fe2+ is present which impart red colour to haemoglobin.
The Fe2+ is attached by four coordinate bonds to the four pyrrole rings and by two more coordinate bonds to the globin (α or β) chain. One of the coordinate bonds, by which it is attached to the globin chain is displaced by molecular oxygen and consequently, oxyhaemoglobin is formed. Due to its oxygen carrying function haemoglobin is known as a respiratory pigment.
The haemoglobin containing two each of a and b globin chains is termed as adult haemoglobin (haemoglobin A). The b globin chain in 25% of adult haemoglobin is substituted by d globin chain. In foetus, however, the b globin chains are substituted by g chains. This haemoglobin has been referred to as fetal haemoglobin (haemoglobin F).
Question 5.
Erythrocyte
Answer:
Erythrocyte Abnormality
(i) Polycythemia Increased number of erythrocytes.
(ii) Anemia Decreased number of erythrocytes. It is further of various types as follows
- Aplastic Anemia Destruction of bone marrow stem cells by chemicals, such as benzene, arsenic and radiation.
- Microcytic Anemia The erythrocytes remain smaller and hence, contain less haemoglobin than normal.
- Haemolytic Anemia Excessive destruction of erythrocytes.
- Pernicious Anemia Sub-normal absorption of vitamin-B12 (cyanocobalamine) from the intestine due to a lack of intestinal protein, intrinsic factor, which assist in its absorption. Vitamin B12 helps in erythrocyte formation.
Question 6.
Anemia
Answer:
Anemia Decreased number of erythrocytes. It is further of various types as follows
- Aplastic Anemia Destruction of bone marrow stem cells by chemicals, such as benzene, arsenic and radiation.
- Microcytic Anemia The erythrocytes remain smaller and hence, contain less haemoglobin than normal.
- Haemolytic Anemia Excessive destruction of erythrocytes.
- Pernicious Anemia Sub-normal absorption of vitamin-B12 (cyanocobalamine) from the intestine due to a lack of intestinal protein, intrinsic factor, which assist in its absorption. Vitamin B12 helps in erythrocyte formation.
Question 7.
Thalasemia
Answer:
Thalassemia An autosomal recessive disease, occurring due ro mutation or deletion of genes. Polypcptides are normal, there is decreased synthesis of α or ß-globin accordingly the disorder is either α-thalassemia or ß-thalasemia
Question 8.
Erythropoiesis
Answer:
Erythropoiesis The process whereby a fraction of primitive stem cells becomes committed towards the development of RBCs lineage. It involves specialised functional and structural differentiation. Approx 2.5 million RBCs are produced every second to replenish the dead cells in spleen and liver. The principle factor regulating erythropoiesis is hormone erythropoietin secreted by the kidneys.
Question 9.
Bone marrow transplantation
Answer:
These are the most abundant of all cells found in the blood. They are red in colour due to the presence of a pigment called haemoglobin, which acts as an oxygen carrier. The formation of RBCs take place in the red bone marrow in adults.
Shape, Size and Structure RBCs are biconcave, disc-shaped cells with the diameter of about 7-8 micron. The shape of RBC is slightly variable. As there are no cell organelles found in it, whole volume is filled with haemoglobin. A healthy individual has about 12-16 gm of haemoglobin in every 100 mL of blood.
When suspended in a suitable medium, erythrocytes pile up one above the other forming rouleaux.
Number In men, the average number of RBC is about 5-5.5 million per cubic millimeter (mm³) of blood.
In women, the average number is about 4-4.5. mm³ of blood.
Lifespan of RBC Total lifespan of RBC is 120 days. After which RBC becomes non-functional and gets destroyed in’spleen. Thus, spleen is also referred as the graveyard of RBCs.
Question 10.
Neurogenic heart
Answer:
Neurogenic Heart: In neurogenic heart muscle cells are incapable of initiating the heartbeat and a group of nerve cells (ganglion) are required to initiate the heart beat, e.g. arthropods and molluscs.
Question 11.
Pacemaker
Answer:
Pacemaker The sinoatrial node or SA node is the pacemaker of the heart. It is a small flattened patch of specialised tissue present in the right upper corner of the right atrium.
It generates electrical impulses (autoexcitable) which spreads in all directions of the heart i.e. it initiates contraction and relaxation of both auricles and ventricles. The sino-atrial node can generate maximum number of action potential, i.e. 70-75 mm, It is responsible for initiation and maintenance of the rhythmic contractile activity of the heart, hence also called as pacemaker of the heart.
Question 12.
Artificial pacemaker
Answer:
Artificial pacemaker When SA node fails to generate electrical impulses, the and heart can undergo serious consequences like cardiac arrest. In such cases, an artificial electrical stimulator called pacemaker, is introduced in the body to regulate the working of heart or generation of heart beats.
The artificial pacemaker is implanted under the skin, near the shoulders, connected with wires implanted in the heart. It regulates the impulses for number of heartbeats per minute.
Question 13.
Heart sounds
Answer:
During each cardiac cycle, two prominent sounds are produced which can be easily heard by a stethoscope (an instrument used for the amplification of sound). This allows to hear the sound and pulse of an individual. The basic reason for the production of these sounds is the closure of various valves. The sounds produced during each heartbeat are as follows
- LuBB: It is the first sound, being produced when inter auriculoventricular valves (tricuspid and bicuspid valve) are closed. This marks the end of the atrial systole and beginning of ventricular systole.
- DuPP: It is the second sound being produced when semilunar valves (of aorta and pulmonary artery) get closed. This marks the end of ventricular systole.
A Third (S3) and fourth (S4) sound also occur in normal individuals called gallops. S3 is associated with early diastolic felling, while S4 with late diastolic.
Question 14.
Cardiac output
Answer:
We have just studied that, our heart beats for about 72 times per minute (on an average). This concludes that in a single minute, many cardiac cycles are performed. Thus, deducing that duration of a each cardiac cycle is 0.8 s. During each cardiac cycle (i.e. in one beat) each ventricle pumps out about 70 mL of blood. This is known as stroke volume.
The volume of blood pumped out by each ventricle in one minute is called cardiac output. Thus, Cardiac output = Stroke volume X Numbers of beats /min.
The cardiac output is 5040 mL or appro × 5L in a normal individual.
It is to be noted that the body has the ability to alter stroke volume as well as the heart rate and thereby, the cardiac output. Athlete has much higher cardiac output than the normal man.
Question 15.
Electrocardiogram
Answer:
Electrocardiogram is a graphical representation of the electrical activity of the heart during a single cardiac cycle. It is obtained by a machine known as electrocardiograph.
Question 16.
Agglutination reaction
Answer:
Agglutination Reactions Agglutination reactions are visible expression of antigen-antibody interactions. For these reactions, a particular test antigen must be conjugated with a carrier (artificial like latex or biological like RBCs).
These conjugated antigens reacts with patient’s serum containing antibodies (if present). The result is observation of clumping due to antigen-antibody complex formation. Various agglutination tests are employed in diagnostic immunology like latex agglutination, direct bacterial agglutination, hemeagglutination, etc.
Question 17.
Anticoagulants
Answer:
Anticoagulants The substances that retards or inhibits the coagulation of the blood. Also known as blood thiners, these prolong the clotting time.
These can be naturally occurring like heparin and antiprothrombins which does not allow the blood to coagulate flowing inside the vessels.
Artificially occurring anticoagulant is EDTA (Ethylene Deimine Tetra Acetic Acid), a calcium chelating agent used in preservation of blood samples.
Anticoagulants inhibit the coagulation cascade by clotting factors that occurs after initial platelet aggregation.
Question 18.
Hemophilia
Answer:
Haemophilia It is a sex linked recessive disorder, the gene for which is present on X chromosome.
It is transmitted from an unaffected carrier female to some of the male offspring. The continues bleeding for long time than normal even due to a small affected individuals, injury because of defective blood coagulation.
Haemophilia is of two types
(i) Haemophilia A occurs due to deficiency of factor (VIII), a clotting protein (anti haemophilic factor) which in conjugate, active of factor (X) .
(ii) Haemophilia B occurs due to deficiency of factor (IX) (Plasma thromboplastin component )or Christmas factor.
Question 19.
Hypertension
Answer:
Hypertension: The pressure exerted by the flow of blood on the elastic walls of the arteries is known as blood pressure. Hypertension is the term used for blood pressure higher than the normal.
The normal blood pressure in humans is measured as 120/80 mmHg (millimetres of mercury pressure), in which 120 mmHg is the systolic pressure (pumping pressure), while, the 80 mmHg is the diastolic pressure (or resting pressure). ,
Persistent increase in blood pressure above 140 mmHg (systolic) and 90 mmHg (diastolic) is termed as hypertension.
Question 20.
Ischemic heart disease
Answer:
Ischemic Heart Disease Ischemic heart disease also known as coronary artery disease is a condition that affects the blood supply to the heart.
Mostly atherosclerosis leads to ischemic heart diseases wherein the blood vessels get narrowed or blocked due to deposition of cholesterol on their walls. This reduces oxygen and nutrient supply to the heart muscles; essential for normal functioning of heart. Eventually part of heart becomes dead often resulting in a heart attack. This also affects the oxygen supply to other vital organs like brain, liver and kidney, etc.
Question 21.
Atherosclerosis
Answer:
It is a disease where arteries get hardened due to deposition of calcium salts in their wall due to which calcium salts precipitate with cholesterol forming plaques. These plaques make the walls of the arteries hard. Healthy arteries are flexible, strong and elastic. In some cases, the hardened wall may crack making the internal wall rough.
This may lead to formation of thrombosis. Arteriosclerosis is an age related disease and may lead to increase in systolic blood pressure. Smoking and obesity are two major factors which may lead to arterioscloresis.
Question 22.
Congestive heart failure
Answer:
Congestive heart failure is a chronic progressive condition affecting the pumping action of heart muscles. It especially refers to the stage where fluid build up starts around the heart causing inefficient pumping of blood. Congestive heart failure develops when ventricles can’t pump blood in sufficient volume to meet the requirement of body due to weakening of its muscles. The main symptom of CHF is congestion of lungs.
Question 23.
Lymphatic system
Answer:
It is an elaborate network of lymph vessels lymph capillaries and lymph nodes, which collects the interstitial fluid (tissue fluid), along with some protein molecules and drains it back into the major veins.
The lymphatic vessels are present in all tissues (except the central nervous system and cornea).
Img 3
Structure of the lymphatic system in close association with the cardio-vascular system
Like blood capillaries, lymphatic vessels are lined by endothelium, but these are closed ended, i.e. these are not drained by vessels. Structurally, lymph vessels resembles the veins, i.e. they have three layers provided with valves at regular intervals to regulate unidirectional flow of lymph. Before draining into veins the lymph is filtered in lymph nodes. Lymph nodes contain lymphocytes.
Question 24.
Myocardial infarction
Answer:
Myocardial infarction is the irreversible death of (necrosis) of heart muscles due to prolonged lack of oxygen supply (ischemia) associated with blockage of coronary artery. These arteries supply oxygenated blood to heart muscles, without which the muscles supplied by blocked artery begins to infarct (die).
The most common causes of myocardial infarction is atherosclerosis, i.e. a accumulation of fatty plaque inside the artery. The damaged calls can not be repaired nor.be regenerated. MI is detected by the changing pattern of the S-T segment of the ECG. Also measuring the plasma concentrations of enzymes, creative phosphokinase (CPK) and lactate dehydrogenase ,(LDH) helps in diagnosis of MI.
Question 25.
Blood coagulation
Answer:
Blood coagulation When an injury occurs, it is stopped by a process called blood clotting or coagulation. It is the function of blood platelets and other factors present in blood. It occus in three steps.
1. Thromboplastin, help in formation of an enzyme prothrombinase (which inactivates heparin) that converts the inactive plasma protein, i.e. prothrombin into its active form thrombin.
2. Thrombin thus, acts as a proteolytic enzyme to convert fibrinogen molecule (produced from the liver in the presence of vitamin – K) to form insoluble fibrin monomer. This reaction requires thrombokinase.
3. These fibrin monomers polymerise to long, sticky fibres. The fibrin threads forms a fine network of threads called fibrins, in which dead and damaged formed elements of blood are trapped.
This finally leads to the formation of a clot or coagulum, which is a dark reddish brown scum formed over the surface of injury.
Question 26.
ABO blood groups
Answer:
It was reported by Karl Landsteiner. It is based on the presence or absence of antigen A or antigen B on the surface of RBCs.
People with blood group A have the antigen A on the surface of their RBCs and have antibodies against antigen B in their plasma. While in the people having blood group B, the case is just vice-versa.
Apart from both these blood groups (i.e. A and B) people with blood group AB have both antigen A and B on their RBCs surface and no antibodies for either of the antigens in their plasma.
In people with blood group O, both antigen A and B are not present on their RBCs, but they have both A and B antibodies against the plasma.
A, B and O blood groups were discovered by Landsteiner (1900). Blood group AB was discovered by de Castello and Steini (1902).
Differentiate between
Question 1.
Plasma and Serum
Answer:
Plasma and Serum
| Plasma |
Serum |
| Plasma is a straw yellow coloured fluid component of blood containing all types of organic and inorganic solutes in dissolved state. |
Serum is clear, watery fluid released from a wound after bleeding and clot formation. |
| Plasma contains fibrinogen which helps in blood clotting |
Serum is without fibrinogen and other coagulation factors. |
Question 2.
Blood and Lymph
Answer:
Blood and Lymph
| Blood |
Lymph |
| It is red in colour due to the presence of haemoglobin in red cells. |
It is colourless as red blood cells are absent. |
| It consists of plasma, RBC, WBC and platelets. |
It consists of plasma and very low number of WBC. |
| Glucose concentration is low. |
Glucose concentration is higher than blood. |
| Clotting of blood is a fast process. |
Clotting of lymph is comparatively slow. |
Question 3.
Open circulation and Closed circulation
Answer:
Open circulation and Closed circulation
| Open Circulation |
Closed Circulation |
| The blood is pumped by the heart into the blood vessels that open into blood spaces (sinuses). |
The blood is pumped by the heart into closed blood vessels. |
| Blood is in direct contact with the tissue cells. |
Blood does not come in direct contact with the tissue cells. |
| Exchange of respiratory gases, nutrients and waste products occurs directly between blood and tissues. |
Exchange of respiratory gases, nutrients and waste product between tissues and blood occur via tissue fluid. |
| Blood returns to the heart slowly. |
Blood returns to the heart rapidly. |
| Respiratory pigment, if present, is dissolved in blood plasma. |
Respiratory pigment is present and may be dissolved in plasma but is usually held in red blood corpuscles. |
Question 4.
Single circulation and Double circulation
Answer:
Single circulation and Double circulation
| Single circulation |
Double Circulation |
| The blood completes only one circuit of circulation, i.e. blood passes through heart only once. |
The blood circulates twice through the heart, i.e two circuits of circulation pulmonary and systemic. |
| The heart is called venous, as it contains only venous blood. |
Heart contains both the two arterial and venous blood. |
| Single circulation occurs in organisims with two chambered heart, e.g. cyclostomes and fishes |
Double circulation occurs in four chambered heart with two atriums and two ventricle e.g. Humans and tetrapods. |
Question 5.
Haemolysis and Crenation
Answer:
Haemolysis and Crenation
| Haemolysis |
Crenation |
| The process of destruction of red blood cells is called haemolysis |
The process of developing irregularities on the surface of RBCs due to cell contraction. |
| It occurs in hypotonic medium due to endo-osmosis |
It occurs in hypertonic medium, due to exo-osmosis. |
| The cell swells up and ultimately burst releasing the haemoglobin in surrounding medium. |
The cell shrinks and develops irregularities these shrunken RBC are called as Echinocytes. |
Question 6.
Adult haemoglobin and Fetal haemoglobin
Answer:
Adult haemoglobin and Fetal haemoglobin
| Adult Haemoglobin |
Fetal Haemoglobin |
| HbA is the form of haemoglobin expressed after birth till the death |
Hbf is the predominant form of haemoglobin expressed in the developing foetus. |
| HbA contains two chains each of α and β sub units where β-globin chain is substituted by d- globin chain. |
Hbf also contains two chains of each α and β globin However, β-globin chains are substituted by g- chains. |
| HbA has lesser affinity for oxygen compared with Hbf |
Hbf has higher affinity for oxygen. |
Question 7.
Granulocytes and Agranulocytes
Answer:
Granulocytes and Agranulocytes
| Granulocytes |
Agranulocytes |
| The leucocytes containing granules in their cytoplasm. |
The type of leucocytes which lack granules in their cytoplasam |
| They have regularly lobed nucleus. |
The nucleus is either rounded or qval. |
| These develops from red bone marrow. |
Agranulocytes develops from lympoid tissue. |
| Granulocytes are of three types, i.e. neutrophils, eosinophils and basophils. |
These are of two types i.e lymphocytes and monocytes. |
Question 8.
Sickle cell anemia and Haemolytic anemia
Answer:
Sickle cell anemia and Haemolytic anemia
| Sickle-cell Anemia |
Hemolytic Anemia |
| An autosome linked recessive trait where a particular mutation in haemoglobin molecule causes RBC to assume sickle-shape |
A form of anemia where low RBC count occurs due to excessive destruction of RBCs. |
| It is caused by the substitution of glutamic acid by valine at the 6th position ofp globin chain of haemoglobin. |
It may be due to mechanical causes, infection, autoimmune disorders or congenital abnormalities in the RBCs. |
Question 9.
Pulmonary circulation and Systemic circulation
Answer:
Pulmonary circulation and Systemic circulation
| Pulmonary Circulation |
Systemic Circulation |
| It is smaller circuit, which carries blood to the lungs and back to the heart. |
It is a larger circuit, which supplies blood to the various parts of the body and back to the heart. |
| It carries deoxygenated blood to the lungs for oxygenation. |
It supplies oxygenated blood to all parts of the body. |
| The blood is pumped by right ventricle and received by left atrium. |
The blood is pumped by left ventricle and received by the right atrium. |
Question 10.
Bicuspid and Tricuspid valves
Answer:
Bicuspid and Tricuspid valves
| Bicuspid Valve |
Tricuspid Values |
| It is formed by two muscular flaps or cusps. |
It is formed by three cusps or leaflet like muscular structure. |
| It guards the opening between the left atrium and left ventricle. |
Tricuspid guards the opening between the right atrium and ventricle. |
Question 11.
Systole and Diastole
Answer:
Systole and Diastole
| Systole |
Diastole |
| The pressure that the blood exerts on the vessels and arteries around the body, during the heartbeats, i.e. when heart is contracting. |
Diastolic pressure measures the pressure exerted by the blood on walls of arteries when the heart is relaxed. |
| Average range is 90-120 mm Hg (adults), 95 mm Hg (infants). |
Average range is 60-80 mm Hg (adults) 65 mm Hg (Infants) |
| Left ventricles during systole contracts. |
Ventricles of the heart fills up with blood. |
| Systole constitutes the maximum pressure in the arteries. |
Diastolic blood pressure constitutes the minimum pressure in the arteries. |
Question 12.
SA node and AV node
Answer:
SA node and AV node
| SA Node |
AV Node |
| It is located at the upper lateral wall of right auricle. |
It is situated at the base of right auricle, near auriculovetricular junction. |
| It generates impulses to initiate heart beating. |
Normally it does not generate impulse, but strengthen them. |
| SA node is also called pacemaker. |
AV node is also called pacesetter. |
| It supplies signals directly to auricles. |
It supplies signals to ventricles. |
| It is not associated with bundle of His and Purkinje fibres. |
It is associated with bundle of His and Purkinje fibres. |
Question 13.
Hemophilia A and Hemophilia B
Answer:
Hemophilia A and Hemophilia B
| Hemophilia A |
Hemophilia B |
| It is caused by deficiency of factor (VIII). |
It is caused by deficiency of factor IX. |
| Also known as the classic hemophilia it is very common in occurrence. |
It is also known as Christmas disease and it is very rare in occurrence. |
Question 14.
Haemoglobinopathy and Thalasemia
Answer:
Haemoglobinopathy and Thalasemia
| Haemoglobinopathy |
Thalasemia |
| A genetic defect resulting in abnormal structure of one of the globin chains of hemoglobin. |
An autosome linked recessive disease occurring due to either mutation or deletion of genes resulting in reduced rate of synthesis of one of the globin chains. |
| Abnormal polypeptides are produced. |
The polypeptides are normal. |
| Abnormal haemoglobin produced due to mutant genes are identified as haemoglobin C, E, I, J and S, etc. |
If there is decreased synthesis of α-globin it is known as α- thalassemia – if β-globin synthesis decreases it is called β-thalassemia. |
Question 15.
Arteriosclerosis and Atherosclerosis
Answer:
Arteriosclerosis and Atherosclerosis
| Arteriosclerosis |
Atherosclerosis |
| The thickening, hardening and loss of elasticity of arterial walls |
It is a specific type of arteriosclerosis. It refers to buildup of fats, cholesterol and other substances in the artery walls. |
| Due to occlusion of the arterial lumen, total peripheral resistance increases, leading to hypertension and heart failure. |
Atherosclerosis progress towards heart failure, coronary artery disease and ischemic heart disease. |
Question 16.
Flutter and Fibrillation
Answer:
Flutter and Fibrillation
| Flutter |
Fibrillation |
| The atrium beats regularly, but faster than the usual and more than ventricles. |
The atria beats irregularly. |
| Less common in occurrence. |
Commonly occurs in old age people who have heart conditions associated with atrial contraction. |