Prasanna

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 16 Digestion and Absorption Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 16 Question Answer Digestion and Absorption

Digestion and Absorption Class 11 Questions and Answers CHSE Odisha

Multiple Choice Questions

Question 1.
Glucose is stored as glycogen in
(a) pancreas
(b) liver
(c) stomach
(d) kidney
Answer:
(b) liver

Question 2.
Ascorbic acid is also known as
(a) vitamin-B
(b) vitamin-C
(c) vitamin-E
(d) vitamin-D
Answer:
(b) vitamin-C

Question 3.
Which gland function as both exocrine and electrone glands?
(a) Salivary gland
(b) Gastric gland
(c) Pancreas
(d) Liver
(c) Pancreas

Question 4.
Pepsinogen is activated by
(a) trypsin
(b) chymotrypsin
(c) hydorchloric acid
(d) pepsin
Answer:
(c) hydorchloric acid

Question 5.
Trypsin converts
(a) fats into fatty acids
(b) proteins into peptones
(c) polysaccharides into maltose
(d) peptones into amino acids
Answer:
(b) proteins into peptones

Question 6.
The end products of fat digestion are fatty acids and
(a) glycerol
(b) cholesterol
(c) phospholipid
(d) glycolipid
Answer:
(a) glycerol

Question 7.
The posterior free part of the soft palate is known as
(a) glottis
(b) gullet
(c) epiglottis
(d) uvula
Answer:
(d) uvula

Question 8.
The number of teeth in the deciduous set of human being is
(a) 32
(b) 20
(c) 18
(d) 24
Answer:
(b) 20

Question 9.
The opening of the middle ear into the pharynx is known as
(a) eustachian opening
(b) external nostril
(c) internal nostril
(d) glottis
Answer:
(a) eustachian opening

Question 10.
The gastrointestinal hormone that stimulates the contraction of the gall bladder is known as
(a) gastrin
(b) chloecystokinin
(c) secretin
(d) molitin
Answer:
(b) chloecystokinin

Question 11.
The wall of the stomach of human is histologically unique in possessing
(a) submucosa
(b) circular muscle
(c) longitudinal muscle
(d) oblique muscle
Answer:
(a) submucosa

Question 12.
Gastrin is secreted from the mucosa of
(a) antrum
(b) fundus
(c) body
(d) pylorus
Answer:
(d) pylorus

Question 13.
Brunner’s glands are present in the mucosa of
(a) ileum
(b) jejunum
(c) duodenum
(d) colon
Answer:
(c) duodenum

Question 14.
Secretin stimulates the release of
(a) bicarbonate ions into the pancreatic juice
(b) water into the pancreatic juice
(c) enzymes into the pancreatic juice
(d) Ca2+into the pancreatic juice
Answer:
(a) bicarbonate ions into the pancreatic juice

Question 15.
Kwashiorkor, a nutritional disorder, caused due to the deficiency of
(a) carbohydrates
(b) lipids
(c) vitamins
(d) proteins
Answer:
(d) proteins

Question 16.
In a polypeptide, the amino acids are joined together by
(a) glycosidic bonds
(b) phosphodiester bonds
(c) peptide bonds
(d) hydrogen bonds
Answer:
(c) peptide bonds

Very Short Answer Type Questions

Question 1.
Name the mass of vascular connective tissue in a tooth.
Answer:
Pulp cavity

Question 2.
Name the water soluble vitamins.
Answer:
Vitamin-B, vit-C.

Question 3.
Enlist the fat soluble vitamins.
Answer:
Vit-A, vit-D.

Question 4.
Name three divisions of the small intestine.
Answer:
Duodenum, jejunem and ileum.

Question 5.
Name the vestigial organ in the alimentary canal of human.
Answer:
Appendix

Question 6.
Which gland is the largest gland of the body?
Answer:
Liver

Question 7.
Name the term used for the presence of different types of teeth.
Answer:
Heterodont dentition.

Question 8.
Name two bile pigment.
Answer:
Bilirubin and Bilivirdin.

Question 9.
How many liver lobes are there in human?
Answer:
2

Question 10.
Name the ampulla formed by the joining of the common bile duct and pancreatic duct before opening into the duodenum.
Answer:
Ampulla of vater

Question 11.
Name the phagocytic cell in the liver.
Answer:
Kupffer cells

Question 12.
What is the non-digestive enzyme released in the small intestine?
Answer:
Trypsinogen

Question 13.
Name the enzyme that digest fat.
Answer:
Lipase

Question 14.
Name the structure that is formed by the grouping of hepatic artery, hepatic portal vein and bile duct in the liver.
Answer:
Portal triad

Question 15.
Give an alternate name for ptyalin.
Answer:
Salivary amylase

Question 16.
Name the end proudct of protein digestion.
Answer:
Amino acids

Question 17.
Name the intestinal glands, which secrete succus entericuus.
Answer:
Crypts of Lieberkuhn

Fill in the Blanks

Question 1.
The fibrous connective tissue that cements the root of the tooth to the socket is known as …………….. .
Answer:
Enamel

Question 2.
The last molar teeth in human are known as ………… teeth.
Answer:
Wisdom

Question 3.
………… is the hardest substance in the human body.
Answer:
Enamel

Question 4.
The longitudinal folds of the oesophageal mucosa are known as …………… .
Answer:
Oesophageal rugal

Question 5.
The passage of the bolus through the lumen of oesophagus in spurts is known as ………….. .
Answer:
Peristalsis

Question 6.
The opening of the common bile duct and pancreatic duct into the duodenum is guarded by a sphincter, called ………….. .
Answer:
Sphincter of addi

Question 7.
The gastrointestinal hormone that stimulates the secretion of enzymes into the pancreatic juice is known as …………. .
Answer:
Pancrozymin

Question 8.
The connective tissue sheath, surrounding a liver lobule is known as ……………. .
Answer:
Glisson’s capsule

Question 9.
Bile facilitates the digestion of fat by dividing large fat droplets into a number of smaller droplets. This function of bile is known as ………… .
Answer:
Emulsification

Question 10.
Intestinal juice is alternately known as …………… .
Answer:
Succus entericus

Question 11.
There are ………… pairs of salivary glands in human.
Answer:
3

Question 12.
………….. is the substrate for ptyalin.
Answer:
Starch

Question 13.
The yellow colour of the stool is due to the presence of a pigment ……………. .
Answer:
Bilirubin

Question 14.
Limit dextrinase or a-Dextrinase is alternately known as ………….. .
Answer:
Isomealtase

Question 15.
Synthesis of glucose from non-carbohydrate sources is known as ……………. .
Answer:
Gluconeogonesis

Question 16.
Rennin acts on the milk protein …………. and changes it into …………… in the presence of Ca2+.
Answer:
Paracasein, calcium paracaseinate

Question 17.
Bile is secreted by ………… and stored in ………….. .
Answer:
Liver, gall bladder

Question 18.
The coagulation factors, prothrombin and fibrinogen are synthesised in ………….. .
Answer:
liver

Match the Words

Group A	GroupB
1. Chief cell	(a) Small intestine
2. Meissner’s plexus	(b) Insulin
3. Trypsinogen	(c) Bilirubin
4. Indigestion	(d) Food poisoning
5. Islets of Langerhans	(e) Pepsinogen
6. Marasmus	(f) HCl
7. Jaundice	(g) Lacteal
8. Chyle	(h) Pancreatic juice
9. Fatty acid	(i) Sub-mucosa
10. Oxyntic cell	(j) Nutritional deficiency

Answer:

Group A	GroupB
1. Chief cell	(e) Pepsinogen
2. Meissner’s plexus	(i) Sub-mucosa
3. Trypsinogen	(h) Pancreatic juice
4. Indigestion	(d) Food poisoning
5. Islets of Langerhans	(b) Insulin
6. Marasmus	(j) Nutritional deficiency
7. Jaundice	(c) Bilirubin
8. Chyle	(a) Small intestine
9. Fatty acid	(g) Lacteal
10. Oxyntic cell	(f) HCl

Short Answer Type Question

Question 1.
What do you mean by intracellular digestion?
Answer:
Intracellular Digestion
It is the simplest type of digestion, which occurs entirely inside the cell. The food material is engulfed by the cell into a food vacuole. Then lysosomes containing digestive enzymes fuse with the food vacuole and consequently the food is digested. The digested products are absorbed into the surrounding cytoplasm by simple diffusion. The residual undigested food is eliminated to the outer side by egestion (e.g. all protozoans, sponges and Hydra).

Posterior end

Question 2.
Explain the gustatory function of the tongue.
Answer:
Tongue acts as a gustatory organ for perceiving taste. It bears numerous taste buds (organ of taste). The circumvallate papillae of tongue bear around 100 taste buds/papilla. These taste buds open on tongue’s surface through a gustatory pore.

Question 3.
Write the dental formula of the permanent set of man.
Answer:

Question 4.
Write the sub-divisions of the pharynx and the openings discharging into the pharynx and the openings leading from the pharynx.
Answer:
Pharynx possess 3 divisions namely nasopharynx, oropharynx and laryngopharynx.
The opening discharging into pharyx is called buccopharyngeal cavity.
The openings leading from pharynx are gullet (into oesophagus) and glottis (into larynx).

Question 5.
Mention about the divisions of the stomach of man.
Answer:
Human stomach is divided into 4 regions namely cardiac part (Cardia), fundus, body and pyloric part (Pylorus).

Question 6.
What do you mean by peristalsis and antiperistalsis?
Answer:
Peristalsis is successive contraction and relaxation of oesophageal muscle layers through which food is conducted to the stomach.
Antiperistalsis is the contraction and relaxation in a reverse rhythm. It results in hiccups.

Question 7.
What are Peyer’s patches and what is their function?
Answer:
Peyer’s Patches are small nodules of lymphoid tissue in the ileum. It is the place of maturation of bone marrow lymphocytes as B-lymphocytes. ,

Question 8.
What are the four histological layers in the alimentary canal of man from outer to inner?
Answer:
Histological layer of alimentary canal from outer to inner side are mucosa, submucosa, muscularis externa and serosa.

Question 9.
How is the secretion of the gastric juice regulated?
Answer:
As soon as the food bolus reaches ,the stomach, the enteroendocrine cells of the antral mucosa secrete a hormone called gastrin. It stimulates the gastric glands to produce gastric juice. The gastric juice consist of mucus, hydrochloric acid (HC1), proenzymes-sinogen and pro-rennin, and gastric lipase.

Question 10.
Pancreas is a mixocrine gland. Explain it.
Answer:
Pancreas functions both as an exocrine and an endocrine gland. Hence, it is a mixocrine gland.
Its exocrine part possess acini which secrete pancreatic juices. The endocrine part possess Islet of Langerhans.

Question 11.
If enterokinase does not have a hydrolytic function in digestion, what specific role does it play?
Answer:
Enterokinase is present in pancreatic juices secreted by acini or lobules. It is an intestinal activator enzyme which activates trypsinogen into trypsin.

Question 12.
What are the physiological roles of insulin and glucagon? Where are these hormones secreted from the pancreas?
Answer:
Insulin and glucagon are two antagonistic hormones secreted by P-cell and a-cells of I-slet of Langerhans respectively.
Insulin lowers the blood glucose and glucagon promotes glucose formation in body.

Question 13.
Distinguish between glycogenesis and glycogenolysis.
Answer:
Glycogenesis It converts excess glucose into glycogen with the action of insulin hormone.
Glycogenolysis It converts glycogen into glucose with the action of glycogen hormone.

Question 14.
What do you understand by curdling of milk?
Answer:
Rennin hydrolyses the milk protein, casein into para-casein and whey protein (peptone-like substance). Paracasein is transformed into soluble calcium para-cascinate in the presence of calcium ions. This is known as clotting or curdling of milk.

Question 15.
What are exo and endopeptidases?
Answer:
All proteases of the pancreatic and intestinal juices fall under 2 broad categories as follows
(a) Eendopeptidase they hydrolyses internal peptide bonds, e.g. trypsin, elastase, etc.
(b) Exopeptidase they hydrolyses peptide bonds from C- or N- ends in a sequence.
e.g. carboxypeptidase.

Question 16.
What do you understand by amino and carboxypeptidases?
Answer:
Aminopeptidases There peptide bonds are hydrolysed by exopeptidase through N-terminus.
Carboyxpeptidases There peptide bonds are hydrolysed by exopeptidases through C-lerminus.

Question 17.
Comment on the absorption of glucose through the intestine following digestion.
Answer:
The end products of carbohydrate digestion, monosaccharides, such as glucose, fructose, galactose, etc., are rapidly absorbed into the blood stream across the wall of the small intestine. This absorption or transport is dependent on the concentration of Na⁺ in the intestinal lumen. A high Na⁺ concentration in the lumen facilitates the transport of glucose into the epithelial cells. Both glucose and Na⁺ are transported into the cells by a membrane transporter (a transporter is a membrane integral pfotein), called cotransporter or more specifically, Sodium Dependent Glucose Transporter (SGLT).

Following the transport into the epithelial cells, Na⁺ is released back into the intestinal lumen, while glucose is released into the cytosol. Thus, glucose absorption is a secondary active transport. The energy for glucose transport is provided by the active transport of Na⁺ out of the cell. The monosaccharides absorbed into the cytosol and then into the interstitium, enter into the hepatic portal circulation.

Question 18.
What are Kwashiorkor and Marasmus related to?
Answer:
Kwashirokor and Marasmus are Protein Energy Malnutrition (PEM) diseases. This nutritional deficiency is caused by the intake proteins of less calorific value for a long time.

Write short notes on

Question 1.
Dental formula of man
Answer:
Dental Formula of Man The number of each type of teeth can be expressed by a dental formula, which is the arrangement teeth in each half of the upper and the lower jaw in order I, C, Pm and M.
Milk teeth of man include 8 incisors, 4 canines and 8 molars. Molars of milk teeth are shed off and premolars of permanent teeth take their place. The permanent teeth are 8 incisors, 4 canines, 8 premolars and 12 molars. Thus,
12 teeth (8 premolars and 4 molars) are monophyodont. Dental formulae of milk teeth and permanent teeth of human are given below \

Dental formula of milk teeth = \(\frac{212}{212}\) x 2 = 20

Dental formula of permanent teeth = \(\frac{2123}{2123}\) × 2 = 32

Question 2.
Salivary glands of man
Answer:
Salivary Glands of Man In man, the salivary glands occurs in three pairs. Parotid, sublingual and submandibular glands. The ducts of parotid gland open into the oral cavity near the upper second molars. The ducts of sublingual gland open into the floor of the oral cavity. Submandibular glands are located at an angle of the lower jaw. Their ducts open into the oral cavity near the lower central incisors.

The parotid glands secrete much of salivary amylase or a-amylase (ptyalin). Sub-lingual and submandibular salivary secrete salivary amylase and mucus.

Question 3.
Larynx
Answer:
Larynx It is commonly called the voice box. These are situated below where the tract of the pharynx splits into the trachea and the oesophagus. Sound is generated in the larynx, and that is where pitch and volume are manipulated.

Question 4.
Pharynx
Answer:
Pharynx It is a small funnel-shaped chamber located behind the oral cavity. It serves as a common passage for both food and air, i.e. it communicates with both oesophagus and trachea.

Question 5.
Peristalsis
Answer:
Peristalsis It is produced by involuntary contraction of circular muscles in the oesophagus lying just above and around the top of the bolus and simultaneous contraction of the longitudinal muscles lying around the bottom of and just below the bolus.
It pushes the food in the forward direction (away from the mouth).

Question 6.
Gastric glands
Answer:
Gastric Glands The glands of stomach are called gastric glands. These are present in the mucosa of the stomach. The gastric gland contains the following three types of secretory cells, i.e.
(a) Mucous or goblet cells, secretes alkaline mucus.
(b) Peptic or chief or zymogenic cells, secretes inactive precursors of gastric enzymes,
(c) Parietal or oxyntic cells, secretes HC1 and castle’s intrinsic factor.

Question 7.
Peyer’s patches
Answer:
Peyer’s Patches Small nodules of lymphatic tissue can be seen along the entire length of the small intestine. In some places, particularly along the ileum, these nodules are clustered together in groups called peyer’s patches. These help in destroying harmful bacteria of the region.

Question 8.
Islet of Langerhans
Answer:
Islet of Langerhans The endocrine part of the pancreas consists of groups of islets of Langerhans. The human pancreas has about one million islets. Each islet of Langerhans consists of four types of cells, i.e. α-cells, ß-cells, δ-cells and pancreatic polypeptides cells (PP cells) α-cells secretes glucagon hormone which converts glycogen into glucose.
ß-cells secrete insulin which converts glucose into glycogen.
δ-cells secrete somatostatin which inhibits the secretion of glycogen and inslulin,
PP cells secrete pancreatic polypeptide whcih inhibits the release of pancreatic juice.

Question 9.
Gastrointestinal hormones
Answer:
Gastrointestinal Hormones The gastrointestinal hormones constitute a group of hormones secreted by enteroendocrine cells in the stomach, pancreas and small intestine.
The gastrointestinal hormones can be divided into three main groups based upon their chemical structure.

• Gastrin-Cholecystokinin Family gastrin and cholecystokinin
• Secretin Family secretin, glucagon
• Somatostatin Family

Question 10.
Protein deficiency disorders
Answer:
Protein Deficiency Disorders Proteins are used as structural components of tissues, as channels, transporters, regulatory molecules and enzymes. Amino acids, the units of proteins, are required for the formation, growth and repair of body cells. It protein are not provided properly, two deficiency diseases named Marasmus and Kwashiorkor are caused in children.

Kwashiorkor is protein deficiency with adequate energy intake whereas marasmus is inadequate energy intake. Protein wasting in kwashiorkor generally leads to edema and ascites, while muscular wasting and loss of subcutaneous fat are the main clinical signs of marasmus.

Question 11.
Absorption of digested food
Answer:
Absorption of Digested Food After the conversion of large and complex food particles into their respective simpler forms, the next step in digestion process is the absorption of these small and simple particles.

It is the process by which end products of digestion pass through the intestinal mucosa into the blood or lymph. The site of absorption is mainly small intestine. Absorption is carried out by the means of diffusion, active, passive or facilitated transport mechanism.
The carbohydrates are mainly absorbed in the form of monosaccharides and proteins in the form of amino acids.

Question 12.
Indigestion
Answer:
Indigestion Indigestion is the process, in which food is not properly digested by digestive system that leads to a feeling of fullness.
The incomplete digestion of food is due to one of the following causes, i.e. inadequate secretion of digestive enzymes and gastrointestinal hormones, anxiety, food poisoning, over eating, spicy food, etc.

Question 13.
Constipation
Answer:
Constipation It is the condition of difficult or irregular defecation during which the faces are retained within the rectum (large intestine) for a longer time the normal. Due to this, more amount of water is absorbed from the faecal matter making it hard and dry to expel out.

During constipation slowing down of peristaltic movements of alimentary canal is visible. A common treatment is a mild laxative, such as milk of magnesia, which induces defecation.

Question 14.
Vomiting
Answer:
Vomiting It is the forceful ejection of harmful contents of stomach through the mouth. It is not due to the reverse peristalsis of the stomach and oesophagus, instead the major thrust or force for expulsion is from the contraction of diaphragm and abdominal muscles. The reflex action of vomiting is controlled by the vomit centre in the medulla.

Question 15.
Jaundice
Answer:
Jaundice It is the condition in which bile pigments begin to excrete through other parts of the body due to their increased accumulation level in the blood. This occurs due to malfunctioning of liver. Thus, the skin and the white portion of sclera of the eyes turns yellow.

Question 16.
Diarrhoea
Answer:
Diarrhoea It is the condition of abnormal frequency of bowel movement (act of defecation) and increased liquidity of faces, which is caused due to irritation in the lining of the colon.

During diarrhoea, the peristalsis movement gets increased due to which the contents of intenstine pass through rapidly. Thus, reducing the absorption of food and water.

Distinguish between

Question 1.
Intracellular and Extracellular digestions
Answer:
Intracellular digestion and Extracellular digestion

Intracellular digestion	Extracellular digestion
The digestion of food occurs within the cell.	The digestion of food occurs outside the cell in the cavity of alimentary canal.
Digestive enzymes are secreted by the surrounding cytoplasm into the food vacuole.	Digestive enzymes.are secreted by special ceils into the cavity of alimentary canal.
Digestive products are diffused into the cytoplasm.	Digestive products diffuse across the intestinal wall into various parts of the body.
It occurs in unicellular organisms.	It occurs in multicellular organisms.

Question 2.
Teeth of Deciduous set and Permanent set
Answer:
Teeth of Deciduous set and Permanent set

Deciduous set	Permanent set
These are temporary.	These are permanent.
These are 20 in number.	These are 32 in number.
It begins to erupt at the age of 6 months.	It begins to erupt at age of 6 year.
These include 8 incisors, 4 canines, and 8 molars.	These include 8 incisors, 4 canines, 8 premolars and 12 molars.
Dental formula \(\frac{212}{212}\) × 2 = 20.	Dental formula \(\frac{2123}{2123}\) × 2 = 32.

Question 3.
Cardiac stomach and Pyloric stomach
Answer:
Cardiac stomach and Pyloric stomach

Cardiac stomach	Pyloric stomach
It is present near the heart, it is upper portion of the stomach.	It is present in the lower portion.
The gastroesophageal sphincter lies in the opening between oesophagus and stomach .	The pyloric sphincter lies in the opening between stomach and duodenum.

Question 4.
Duodenum and Ileum
Answer:
Duodenum and Ileum

Duodenum	Ileum
It is the shortest, widest part of the small intestine.	It is the longest part of small intestine.
It is U-shaped, the hepatopancreatic ampulla opens into the duodenum.	It is greatly coiled.
The function of duodenum is absorption of iron.	It absorbs bile salts, vitamin-B and remaining digested food particles that do not absorb in the jejunum.

Question 5.
Exocrine pancreas and Endocrine pancreas
Answer:
Exocrine pancreas and Endocrine pancreas

Exocrine pancreas	Endocrine pancreas
It consists of rounded lobules.	It consists of groups of islets of Langerhans.
It secretes an alkaline pancreatic juice with pH 8.4.	It secretes various hormones.
Pancreatic juice contains trypsinogen, chymotrypsinogen, elastase, DNase, RNase, etc.	It contains glucagon, insulin, somatostatin hormones.
The pancreatic juice helps in the digestion of starch, proteins, fats and nucleic acids.	Glycogen hormone converts glycogen into glucose, insulin converts glucose into glycogen.

Question 6.
Circumvallate papillae and Filliform papillae
Answer:
Circumvallate papillae and Filliform papillae

Circumvallate papillae	Filliform papillae
These are usually about 8 to 12 in number.	These are numerous.
Each papilla contains upto 100 taste buds.	These papillae contains tactile receptors, but no taste buds.
These are largest.	These are smallest.
These are found on the upper part of the tongue.	These are found mainly near the centre and most of the upper surface of the tongue.

Question 7.
Brunner’s gland and Crypt of Lieberkuhn
Answer:
Brunner’s gland and Crypt of Lieberkuhn

Brunner’s gland	Crypt of Lieberkuhn
These are found only in the duodenum.	These occur throughout the small intestine between the villi.
They secrete a little enzyme and mucus.	They secrete digestive enzymes and mucus.
The Brunner’s glands open into the crypts of Lieberkuhn.	The mucus is secreted by the goblet cells.

Question 8.
Secretin and Pancreozymin
Answer:
Secretin and Pancreozymin

Secretin	Pancreozymin
It was the first hormone to be discovered by scientists.	The word pancreozymin is derived from pancreas and zymin, which means enzyme producer.
It is secreted by the epithelium of duodenum.	It is secreted by the epithelium of entire small intestine.
It increases secretion of bile. It decreases gastric secretion and motality.	It stimulates the gall bladder to release bile and pancreas to secret digestive enzyme.

Question 9.
Exopeptidase and Endopeptidase
Answer:
Exopeptidase and Endopeptidase

Exopeptidase	Endopeptidase
These enzymes break the bonds between amino acids existing at the end of the polypeptide chain.	These enzymes can breafc peptide bonds between the amino acids in a polypeptide chain.
Carboxypeptidase is an exopeptidase.	Pepsin and trypsin are the endopeptidase.
These can breakdown proteins into monomers.	These cannot breakdown peptides into monomers.

Question 10.
Aminopeptidase and Carboxypeptidase
Answer:
Aminopeptidase and Carboxypeptidase

Aminopeptidase	Carboxypeptidase
It is present in intestinal juice.	It is present in pancreatic juice.
The site of action of this enzyme is small intestine.	It also act in small intestine.
It acts on peptides and convert it in amino acids.	It acts on protease and convert it in dipeptides.

Question 11.
α-1, 4 glycosidase and α-1, 6 glycosidase
Answer:
α-1, 4 glycosidase and α-1, 6 glycosidase

α-1,4 glycosidase	α-1,6 glycosidase
It is glucosidase enzyme which asist in hydrolysis of glycosidic bond.	It is also a glucosidase enzyme which asist hydrolysis of glycosidic bond.
It acts on α-1,4 glycosidic bond and release glucose units.	It acts on α-1,6 glycosidic bond it releases monomer.

Long Answer Type Questions

Question 1.
Describe the physiology of digestion of different food stuffs in human digestive system.
Answer:
Digestion in Small Intestine:
To further facilitate the digestion of food, muscularis layer of small intestine starts peristaltic movements This allows a thorough mixing up of food with various secretions in the intestine.
These contractions of muscles in the small intestine allows the further churning and kneading of the chyme , and finally pushing it into the large intestine.

Segmented contracion of the wall of the small intestine

The respective digestive juices from the liver (bile), pancreas (pancreatic juice) and small intestine (intestinal juices) are released into the small intestine to bring out the further chemical simplification of food. The pancreatic juice from the pancreas and the bile from the liver are released through the hepatopancreatic duct.

Digestion in small intestine can be studied under two categories as follows
(a) Digestion in the Duodenum:
In the duodenum, the chyme is mixed with three alkaline juices; bile from the liver, pancreatic juice from the pancreas, and intestinal juice from intestinal glands (crypts of Lieberkuhn); and mucous from the Brunner’s glands. The enteroendocrine cells present in the mucosal layer of the duodenum are stimulated to secrete several gastro-intestinal hormones, when the acidified chyme of the stomach enters into it. Two such hormones bearing significant roles in the release of digestive juices are Cholecystokinin-Pancreozymin (CCK-PZ) and Secretin.

(i) Cholecystokinin-Pancreozymin (CCK-PZ) It is a single hormone possessing two activities. Cholecystokinin (CCK) activity stimulates the gall bladder to contract and release bile into the duodenum, while pancreozymin activity stimulates the acinar cells of the pancreas to secrete increasing amounts of pancreatic juice, rich in enzymes.

(ii) Secretin It stimulates the duct cells of the pancreatic acini to secrete sodium bicarbonate into the pancreatic juice and thus makes the pancreatic juice alkaline.

In addition, enterogastrone is presumed to be a separate, hormone regulating gastro-intestinal functions. However, it is not a separate entity, but rather a collection of two hormones, secretin and cholecystokinin-pancreozymin, which inhibit gastric function.

Action of Panacreatic Juice:
The pancreatic juice secreted from the pancreas contains the various inactive enzymes.
These are as follows
(a) Trypsinogen
(b) Chymotrypsinogen
(c) Procarboxypeptidases
(d) Amylases
(e) Lipases
(f) Nucleases
Trypsinogen is activated by an enzyme enterokinase secreted by intestinal mucosa into active trypsin which in turn activates the other enzymes of pancreatic juice.

The proteins, proteases and peptones (partially hydrolysed form of proteins) present in the chyme (reaching the intestine) are acted upon by the proteolytic enzymes of pancreatic juice. These are given below as

* Carbohydrates in the chyme are hydrolysed by pancreatic amylase into disaccharides.

Nucleases in the pancreatic juice acts on nucleic acids to form nucleotides and nucleosides.

The bile secreted from the liver is released into duodenum of small intestine. Bile contains the bile pigments, i.e. bilirubin and biliverdin, bile salts, cholesterol and phospholipids.
Thus, fats are broken down into di and monoglycerides by the action of lipases secreted by pancreas.

Bile does not contain any enzyme as gastric juice. It helps in emulsifying fats, i.e. in breakdown of fats into very small micelles which are kept suspended in an aqueous medium.
The process of emulsification is basically carried out by the salts of bile. This increases the surface area of fat available for digestion by the lipase (as bile also activates lipases).

Question 2.
Draw a neat labelled diagram of human alimentary canal (Description is not required).
Answer:

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 15 Plant Growth and Development Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 15 Question Answer Plant Growth and Development

Plant Growth and Development Class 11 Questions and Answers CHSE Odisha

Very Short Answer Types Questions

Multiple choices questions

Question 1.
Gibberellic acids show which of the following physiological effects:
(a) yellowing of young leaves
(b) elongation of genetically dwarf plants
(c) shortening of genetically tall plants
(d) yellowing of old leaves
Answer:
(b) elongation of genetically dwarf plants

Question 2.
What will happen when the dark period of short day plants is interrupted by a flash of light?
(a) flower immediately
(b) will not flower
(c) induce more flowering
(d) converts to a long day plant
Answer:
(b) will not flower

Question 3.
The plant hormone connected primarily with cell division is
(a) IAA
(b) NAA
(c) Kinetin
(d) GA
Answer:
(c) Kinetin

Question 4.
Apical dominance is influenced by
(a) GA
(b) Ethylene
(c) Auxin
(d) Coumarine
Answer:
(c) Auxin

Question 5.
Abscisic acid causes
(a) stomatal closure
(b) leaf expansion
(c) root formation
(d) stem elongation
Answer:
(a) stomatal closure

Question 6.
Richmond-Lang effect is due to
(a) auxin
(b) abscisic acid
(c) cytokinin
(d) ethylene
Answer:
(c) cytokinin

Question 7.
Auxin transport is
(a) polar
(b) non-polar
(c) symplastic
(d) apoplastic
Answer:
(a) polar

Fill in the blanks

Question 1.
Fruit ripening is induced by the hormone ……….. .
Answer:
ethylene

Question 2.
Mangrove plants generally show …………. type of germination.
Answer:
viviparous

Question 3.
Florigen is associated with …………. .
Answer:
flowering

Question 4.
The amino acid ………….. is the precursor of ethylene.
Answer:
methionine

Short Answer Type Questions

Question 1.
Apical dominance
Answer:
Auxins perform several functions, these are as follows
(i) Apical Dominance Presence of auxin in higher , concentration (in higher plants) in shoot apex, promotes apical dominance. It is seen commonly in many vascular plants, that presence of apical buds does not allow the lateral buds to grow. They only start developing into branches when the apical bud is removed.

Apical dominance in plants (a) A plant with apical bud intact (b) A plant with apical bud removed

(ii) Initiation of Roots In contrast to stem, higher concentration of auxin inhibits the elongation of shoots, but it initiates more lateral branches of roots.

(iii) Inhibition of Abscission Natural auxins delay abscission of young fruits and leaves and also used to control pre-harvest fruit drop.

(iv) Cell Elongation Auxin stimulates the elongation of cells of shoots.

(v) Promotes Flowering Presence of auxin helps in promoting flowering in some plants, e.g., pineapple, litchi, etc.

(vi) Metabolism Application of auxin can enhance metabolism due to mobilisation of nutrients and growth promoting substances.

Question 2.
Seed dormancy
Answer:
In majority of angiospermic plants, seeds remain in an inactive state and germinate only after a specific period of rest or dormancy.
Thus, dormancy may be defined as, ‘the inactive state of the seed in which growth of the embryo is temporarily suspended for a specific length of time’.
This state of inactivation may be due to some internal factors that inhibit the process of germination. The period of dormancy varies in all the plants.
On the contrary, cereals germinate immediately after harvest and seeds of citrus germinate in situ.

Question 3.
Vernalisation
Answer:
Beside light, the temperature also affects the flowering and other vital phenomenon of plants. It has been observed that there are some plants which do not flower until they are not exposed to low temperature, i.e., thdy depend either qualitatively or quantitatively on exposure to low temperature to flower.

This chilling requirement of the plants for flowering is known as vernalisation. It prevents the precocious reproductive development late in the growing season, enabling plant to have sufficient time to reach the level of maturity.

Long Answer Type Questions

Question 1.
Describe the different types of seed germination.
Answer:
Seed Germination
It is the process by which the dormant embryo of the seed resumes active growth and forms a seedling. It is an irreversible process during which radicle grows out first to establish root. After that, plumule grows to form shoot.
Germination may be of three types

(i) Epigeal Germination
In this type of germination, cotyledons are pushed out of the soil. The cotyledons become green and also perform photosynthesis in addition to food storage.

In dicots, this happens due to the elongation of hypocotyl (stem of germinating seedling between cotyledons and radicle), e.g. bean, castor, mustard, tamarind, sunflower, etc.

Epigeal germination

(ii) Hypogeal Germination
In this type of germination, the cotyledons do not come out of the soil and remain underground. The epicotyl (part of embryonic axis between plumule and cotyledons) elongates first to raise the first leaves out of the soil. The hypocotyl growth is restricted, e.g. all monocots (e.g. rice, maize, wheat, etc) and dicots such as gram, pea, mango, groundnut, etc.

Hypogeal Germination of gram

(iii) Viviparous Germination
It is a special type of germination found growing-in salty lakes, sea coasts and deltas, i.e. in mangrove plants.

Germination in vivipary plants

In this process, seed germinates while still attached to the parent plant.
The radicle elongates considerably and projects out of the fruit while its lower part becomes thick and swollen. Finally, the seedling breaks of the parent plant due to its increasing weight and gets embedded in the muddy soil below.
The lateral roots develop soon at the basal end of the radicle.
It is also called aerial germination, e.g. Rhizophora, Ceriops, Avicennia, etc.

Factors Affecting Seed Germination:
Seed germination is directly affected by various factors. These are as follow:
1. Water
It is very essential as seed cannot germinate unless sufficient amount of water is available. Water is important because

• It activates the enzymes which digest the complex reserve food of the seed.
• It maintains the turgidity of the embryonal cells and helps in cell elongation.
• It helps in the rupturing of the seed coat.
• It is the medium for all physiological processes.

2. Oxygen
It is needed in sufficient quantity for germination.
The seed is activated on absorbing water and carries an aerobic respiration at a higher rate, so a lot of O₂ is consumed. Thus, O₂ is essential for respiration and all other physiological activities.

3. Temperature
Suitable temperature is a necessity for germination as a number of physiological processes occur within seed.
The range of optimum temperature varies greatly in different types of seeds. However, most of the seeds fail to germinate below 0°C and above 50°C. The optimum temperature is 25-30°C in most plants.

4. Light
Most of the plants do not require light for germination. Thus, it is not considered as an essential factor. The effect of light on different seeds led to their categorisation into the three groups as given below:

• Positively Photoblastic These seeds require light for germination, e.g. lettuce.
• Negatively Photoblastic These seeds do not require light for germination (i.e. total darkness is needed). If kept under lighted conditions, they do not germinate, e.g. pumpkin.
• Photoblastic Neutral These seeds germinate equally well under dark as well as in light conditions, e.g. cultivated plants like cucumber, tomato, etc.

Question 2.
Give an account of physiological effects of auxins in plants.
Answer:
Auxins
Auxin (Gk. auxein to grow) was initially isolated from the urine of human, but later on, their presence was also found in plants and was proved to be the first PGR ever known. The real plant auxin is chemically known as Indole -3-Acetic Acid (IAA). The term is also applied to other natural and synthetic compounds having various growth regulating properties. Production of auxin generally takes place in the region of growing apices of the stems and roots from where they migrate to the site of their action.

Note Auxins can move only through cell to cell by diffusion, i.e., they cannot move through vascular tissues.

Types of Auxins:
There are generally two basic categories in which auxins are divided
(i) Natural Auxins
It occurs naturally in plants and fungi, e.g., Indole Acetic Acid (IAA) and Indole Butyric Acid (IBA).

(ii) Synthetic Auxins
These are prepared from synthetic compounds that cause several responses to IAA. They can easily move in all directions inside the plants, e.g., Naphthalene Acetic Acid (NAA), 2, 4- dichlorophenoxyacetic acid (2, 4-D).
All these types of auxins are extensively been used in agricultural and horticultural practices.

Functions of Auxins:
Auxins perform several functions, these are as follows
(i) Apical Dominance Presence of auxin in higher , concentration (in higher plants) in shoot apex, promotes apical dominance. It is seen commonly in many vascular plants, that presence of apical buds does not allow the lateral buds to grow. They only start developing into branches when the apical bud is removed.

Apical dominance in plants (a) A plant with apical bud intact (b) A plant with apical bud removed

(ii) Initiation of Roots In contrast to stem, higher concentration of auxin inhibits the elongation of shoots, but it initiates more lateral branches of roots.

(iii) Inhibition of Abscission Natural auxins delay abscission of young fruits and leaves and also used to control pre-harvest fruit drop.

(iv) Cell Elongation Auxin stimulates the elongation of cells of shoots.

(v) Promotes Flowering Presence of auxin helps in promoting flowering in some plants, e.g., pineapple, litchi, etc.

(vi) Metabolism Application of auxin can enhance metabolism due to mobilisation of nutrients and growth promoting substances.

Applications of Auxins:
As stated, use of synthetic auxins is widely accepted now-a-days in various agricultural and horticultural practices.
Following are the applications of auxins

1. Eradication of Weeds Auxins are used as weedicides and herbicides. Application of 2, 4-dichlorophenoxyacetic acid (2, 4-D) is widely done in order to kill dicotyledonous weeds. It does not affect mature, monocotyledonous plants.
2. Parthenocarpy Auxins are sprayed on to the unpollinated pistil and make them develop into parthenocarpic fruits, which carry a better market values.

Question 3.
Discuss the physiological effects of gibberellings in plants.
Answer:
Gibberellins:
These are another group of plant growth regulators, which are known to be weakly acidic growth hormones. There are more than 100 different gibberellins reported from widely different organisms like fungi and higher plants.

All of them are known to be acidic in nature, thus, they are termed as Gibberellic Acids (i.e., GA, GA₁, GA₂ and so on). However, GA₃ is the most important gibberellic acid which was first to be discovered. It is most extensively studied amongst all gibberellins.

Functions of Gibberellins:
Gibberellins show various important physiological effects

1. Elongation of Intemodes It helps in elongation of the internodes so as to increase the height of the plant. They cause an increase in length of axis and is also used in increasing length of grapes stalks.
2. Elongation of Genetically Dwarf Plants It has been seen that if gibberellins are administered to a dwarf plant (pea, maize, etc), it may help in overcoming dwarfism. It also causes fruits to elongate and improve their shape, e.g., in apples, etc.
3. Bolting The gibberellins also helps in promoting bolting (internode elongation) just prior to their reproductive phase or flowering. If gibberellin is sprayed on rosette plants like beet, cabbage as these plants will show extensive internodal growth and profuse leaf development.
4. Breaking Dormancy It also helps in overcoming natural dormancy in buds, tubers, seeds, etc., and helps them to grow.
   Seed is said to be in the dormant state when it remains dry and non-germinating even if all conditions for germination are available, Thus, by ‘breaking seed dormancy’, we simply mean, to induce the
   germination in seeds.
5. Flowering This can also be induced in long day plants by the action of gibberellins.

Applications of Gibberellins
Gibberellins, apart from showing,varied physiological effects, also have numerous applications.
These are as follows

1. Delays Senescence Gibberellins can delay the ripening of fruits such as in Citrus, apples, etc. This can also be used for safe and prolonged storage of the fruits.
2. Malting Process The process of malting in brewing industry can be speeded up by the use of GA₃.
3. Sugar Yield As carbohydrate is stored in the form of sugar in the stems of sugarcane. Thus, if crop of sugarcane is sprayed with gibberellins. It results in increased internodal length of the stem. This, enhances the increase in the yield of sugarcane as much as 20 tonnes per acre.
4. Early Seed Production When sprayed on juvenille conifers, like Cycas and Pinus gibberellins hasten the maturity period of them leading to early seed production.

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 14 Respiration Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 14 Question Answer Respiration

Respiration Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Multiple choice questions:

Question 1.
The first reaction step in glycolysis, that produces ATP, is catalysed by the enzyme
(a) Hexaokinase
(b) Pyruvate kinase
(c) Phosphoglycerate kinase
(d) Phosphofructokinase
Answer:
(d) Phosphofructokinase

Question 2.
The reaction which links glycolysis with Krebs cycle is catalysed by
(a) Glutamate dehydrogenase
(b) Pyruvate dehydrogenase complex
(c) Citralilyase
(d) Pyruvate kinase
Answer:
(b) Pyruvate dehydrogenase complex

Question 3.
Which of the following respiratory substrates produces per mole the highest number of ATP molecules?
(a) Glucose
(b) Sucrose
(c) Strach
(d) Fatty acid
Answer:
(a) Glucose

Question 4.
The enzyme which splits 6-C compound to 3-C compound during glucolysis is
(a) fumarase
(b) aldolase
(c) ligase
(d) carboxylase.
Answer:
(b) aldolase

Question 5.
Glycolysis takes place in
(a) nucleus
(b) vacuole
(c) cytoplasm
(d) mitochondria
Answer:
(c) cytoplasm

Question 6.
The respiratory quotient, when carbohydrates are used as respiratory substrate, is
(a) 1.0
(b) 0.7
(c) 0.9
(d) 0.3
Answer:
(a) 1.0

Fill in the blanks:

Question 1.
Anaerobic respiration is often known as ……………. .
Answer:
Fermentation

Question 2.
The synthesis of ATP involving the direct transfer of phosphate group from a substrate molecule to ADP is called as ……………. .
Answer:
Substrate level phosphorylation

Question 3.
The formation of ethanol from pyrurate is catalysed by the enzymes ………… and alcohol dehydrogenase.
Answer:
Pyruvate decarboxylase

Question 4.
The reactions of Krebs cycle takes place inside …………… .
Answer:
Mitochondrial matrix

Short Answer Type Questions

Question 1.
Alcoholic fermentation.
Answer:
It occurs in fungi and some higher plants. The incomplete oxidation of glucose is achieved under anaerobic condition by a series of reactions in which pyruvic acid is converted to CO₂ and ethonol

Question 2.
Lactic acid fermentation
Answer:
It occurs in human’s muscles, bacteria, etc. Lactic acid is produced as an end product during the reduction of pyruvate by NADH₂ is oxidised to NAD⁺. This reaction is catalysed by lactic acid dehydrogenase, FMN proteins and Zn²⁺ions.

Question 3.
Substrate level phosphorylation
Answer:
The type of ATP synthesis involving the direct transfer of phosphate group from a substrate molecule to ADP to form ATP is called substrate level phosphorylation. It takes place during the following reactions
(i) When 1,3 bisphosphoglycerate is converted to 3-phosphoglycerate.
(ii) When phosphoenol pyruvate is converted to pyruvic acid.

Question 4.
Chemiosmotic hypothesis
Answer:
It was explained by Peter Mitchell in 1961 for which he was awarded the Noble prize in chemistry in 1978. It explains the molecular mechanism of ATP synthesis by suggesting that, the action of ATP synthase is coupled with proton gradient. It is the action of proton gradient that causes a proton motive force. This force allows ATP synthase to phosphorylate ADP and inorganic phosphate to ATP.

Question 5.
Respiratorory Quotient
Answer:
During aerobic respiration, O₂ is consumed and CO₂ is released. The ratio of the amount of CO₂ evolved to the amount of O₂ consumed in respiration is called respiratory quotient (RQ)

Amount of 02 consumed
The value of RQ depends upon the type of substrate used for respiration
RQ value of different substrates is as follows:
RQ = 1 for carbohydrates
RQ < 1 for fats = 0.7
RQ < 1 for proteins = 0.8 – 0.9

Question 6.
Oxidative phosphorylation.
Answer:
The formation of ATP molecules coupled to the transfer of electrons derived from the oxidation of organic compounds through the mitochondrial electron transport chain is called oxidative phosphorylation.

Long Answer Type Questions

Question 1.
Describe the reaction steps of glycolysis
Answer:
Glycolysis:
Glycolysis (Gr. Glycos-sugar, lysis-splitting), is a stepwise process by which one molecule of glucose (6C) breaks down into two molecules of pyruvic acid (3C).

The scheme of glycolysis was given by Gustav Embden, Otto Meyerhof and J Parnas and is often referred as the EMP pathway. It is a common pathway in both aerobic and anaerobic modes of respiration. But in case of anaerobic organisms, it is the only process of respiration. Glycolysis occurs in the cytoplasm of the cell. During the process glucose gets partially oxidised. In plants, this glucose is derived from sucrose (end product of photosynthesis) or from storage carbohydrates.

During the course of process in plant sucrose is first converted into glucose and fructose by the action of invertase enzyme, after this, these two monosaccharides enter the glycolytic pathway.

Steps Involved in Glycolysis:
In glycolysis, a chain of 10 reactions, occur under the control of different enzymes. These reactions can be categorised in to preparatory (or investment) phase and pay off (energy conserving) phase.
It involves the following steps

Step I Phosphorylation of glucose occurs under the action of an enzyme hexokinase and Mg²⁺ that gives rise to glucose-6-phosphate by the utilisation of ATP.

Step II Isomerisation of this phosphorylated glucose-6-phosphate takes place to form fructose-6-phosphate with the help of an enzyme phosphohexose isomerase (reversible reaction).

Step III This fructose-6-phosphate is again phosphorylated by ATP in order to form fructose 1, 6-bisphosphate in the presence of an enzyme phosphofructokinase and Mg²⁺.
The steps of phosphorylation of glucose to fructose 1, 6-bisphosphate (i.e. from step 1 to 3) activates the sugar thus, preventing it from . getting out of the cell.

Step IV Splitting of fructose 1, 6-bisphosphate takes place into two triose phosphate molecules, i.e. dihydroxyacetone 3-phosphate and 3-phosphoglyceraldehyde (i.e. PGAL). This reaction is catalysed by an enzyme aldolase.

Step V Each molecule of PGAL removes two redox equivalents in the form of hydrogen atom and transfer them to a molecule of NAD⁺ (This NAD⁺ forms NADH + H⁺) and accepts inorganic phosphate (Pi) from phosphoric acid. This reaction in turn leads to the conversion to PGAL (which gets oxidised) to 1, 3-bisphosphoglycerate (BPGA) (reversible reaction).

Step VI 1, 3-bisphosphoglycerate is converted to 3-phosphoglycerate with the formation of ATP.
This reaction is catalysed by an enzyme phosphoglycerate kinase. It is also known as energy yielding process. The formation of ATP directly from metabolites constitutes substrate level phosphorylation (reversible reaction).

Step VII In this step, 3-phosphoglycerate is subsequendy isomerised to form 2-phosphoglycerate, catalysed by enzyme phosphoglyceromutase (reversible reaction).

Step VIII In the presence of enzyme enolase and Mg²⁺, with the loss of a water molecule, 2-phosphoglycerate is converted into Phosphoenol Pyruvate (PEP) (reversible reaction).

Step IX High energy phosphate group of Phosphoenol Pyruvate (PEP) is transferred to a molecule of ADP, by the action of enzyme pyruvate kinase in the presence of Mg²⁺ and K⁺. This in turn produces two molecules of pyruvic acid (pyruvate) and a molecule of ATP by substrate level phosphorylation. The pyruvic acid thus, produced is the key product of glycolysis.

Question 2.
Describe the metabolic fate of pyruvate.
Answer:
Metabolic Fate of Pyruvate:
Pyruvate is the end product of glycolysis. The sequence of reactions leading to the formation of pyruvate from glucose is the common pathway occurring during anaerobic and aerobic respiration. Depending upon the absence or presence of molecular oxygen and the cellular metabolic need, Pyruvate takes up different routes for its metabolism

Metabolic fate of pyruvate under aerobic and anaerobic conditions

In the absence of molecular oxygen, respiratory electron transport chain and oxidative phosphorylation can not function in the mitochondrion because molecular oxygen is the terminal electron acceptor for these two highly coordinated processes. As a result the oxidation of NADH to form NAD does not take place. NAD is available in limited amount in the cell. When whole NAD becomes reduced to NADH in the presence of NAD dependent glyceraldehyde 3-phosphate dehydrogenase, glycolysis can not continue to operate. Under the situation of unavailability of molecular oxygen,glycolysis is the main source of chemical energy (ATP) necessary for cell .survival.

Hence, NAD is required to regenerate or to proceed the glycolysis process. Different organisms and cell type can metabolise pyruvate by fermentation also.

Various microorganisms, bacteria, animals and plants are known to catabolise pyruvic acid into various organic compounds depending upon the specific enzymes they possess.

Some of these types are as follows
(i) During alcoholic fermentation, in fungi (e.g., yeast), and some higher plants, the incomplete oxidation of glucose is achieved under anaerobic condition-by a series of reactions in which pyruvic acid is converted to CO₂ and ethanol.
It is done under two steps
(a) Pyruvic acid is first decarboxylated to acetaldehyde formed in the presence of enzyme pyruvic acid decarboxylase.
CH₃CCOOH → CH₃CHO (Acetaldehyde) + CO₂

(b) This acetaldehyde is further reduced to ethyl alcohol or ethanol in the presence of enzyme, i.e. alcohol dehydrogenase.
CH₃CHO + NADH + H² → C₂H₅OH (Ethanol) + NAD⁺

(ii) During lactic acid fermentation occuring in muscles, organisms like some bacteria produce lactic acid as an end product from pyruvic acid.
During the reduction, the pyruvic acid produced in glycolysis is reduced by NADH₂ to form lactic acid, CO₂ is not produced and NADH₂ is oxidised to NAD⁺. This reaction is catalysed by a lactic acid dehydrogenase, FMN proteins and Zn²⁺ ions.

Major pathways of anaerobic respiration

Likewise, in case of animal cells also (such as muscles) during exercise, when there is inadequate amount of oxygen for cellular respiration, pyruvic acid is reduced to lactic acid in the presence of enzyme lactate dehydrogenase. Thus, in both the processes oxidation of reducing (NADH + H⁺) agent takes place.

Energy Yield in Fermentation:
In both alcoholic and lactic acid fermentation, the energy released is very less, i.e. not more than 7% of the energy is released from glucose and not all of it is trapped as high energy bonds of ATP.
Also, the fermentation processes are proved to be hazardous in nature because either acid or alcohol is produced on oxidation. Apart from this, yeasts may also poison themselves to death if the concentration of alcohol reaches about 13%.

Question 3.
Describe the reaction steps of Krebs cycle.
Answer:
Output of Krebs’ Cycle or Citric Acid Cycle:
During this cycle of reactions, 3 molecules of NAD⁺ are reduced to NADH + H⁺ , and one molecule of FAD⁺ is reduced to FADH₂. And also one molecule of ATP is reduced directly from GTP (by substrate level phosphorylation). For continuous oxidation of acetyl . Co-A, continued replenishment of oxaloacetic acid is necessary. In addition to this, regeneration of NAD⁺ and FAD⁺ from NADH and FADH₂, respectively are also required.
The summary equation for this phase of respiration is as follows

Till now, glucose has been broken down to release C02 and 8 molecules of NADH + H⁺, 2 FADH₂ are synthesised and just 2 molecules of ATP.

Importance of Citric Acid Cycle:
The citric acid cycle is important in the following ways
(i) This is the major pathway for the formation for ATP molecules.
(ii) Many intermediate compounds of this cycle are used in the synthesis of other biomolecules.

Question 4.
Describe the respiratory electron transport chain and explain the mechanism of ATP synthesis.
Answer:
Electron Transport System (ETS):
Electron Transport System (ETS) is the metabolic pathway through which the electron passes from one carrier to another. It occurs in the inner mitochondrial membrane.

Electron Transport System (ETS)

The electron transport system consists of four enzyme complexes, which are arranged in a series on the inner membrane of the mitochondria.
(i) Electrons from NADH produced in citric acid cycle are oxidised by NADH dehydrogenase (complex I) and are transferred to ubiquinone located within the inner membrane of the mitochondria.

(ii) Reducing equivalents are also received by ubiquinone via FADH₂ (complex II), generated during the oxidation of succinate in the citric acid cycle. This reduced ubiquinone (ubiquinol) is then oxidised with the electron transfer to cytochrome-c (small protein attached to the outer surface of the inner membrane). Now, via cytochrome-b, c₁ complex (complex III) cytochrome, acts as a mobile carrier for transfer of electrons between complex III and IV.

(iii) The (complex IV), known as cytochrome-c oxidase complex contains cytochromes-a, a₃ and two copper centres).

During the course of transfer, when’electrons pass from one carrier molecule to another (via complex I to IV) in the electron transport chain, they get coupled to ATP synthase (i.e. complex V) for the production of ATP from ADP and inorganic phosphate. The number of • ATP molecules synthesised depends on the nature of the electron donor.

One molecule of NADH on oxidation provides 3 molecules of ATP while one FADH₂ produces 2 molecules of ATP, because its redox potential is higher than NADH and thus, enters the ETS after bypassing the first site of phosphorylation. The electrons are finally accepted by oxygen having the highest redox potential in the series which along with H⁺ forms water.

Aerobic process of respiration takes place only in the presence of O₂, the role of O₂ is limited at the terminal stage of the process. Yet, the presence of oxygen is vital because it drives the whole process by removing hydrogen from the system.

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 13 Photosynthesis in Higher Plants Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 13 Question Answer Photosynthesis in Higher Plants

Photosynthesis in Higher Plants Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Multiple Choices Questions

Question 1.
Oxygenic photosynthesis does not occurs in
(a) plants
(b) green sulphur bacteria
(c) bryophytes
(d) cyanobacteria
Answer:
(b) green sulphur bacteria

Question 2.
Cyclic electron transfer around PS-I results in the formation of
(a) ATP
(b) NADPH
(c) ATP and NADPH
(d) ATP, NADPH and O₂
Answer:
(a) ATP

Question 3.
In higher plant chloroplasts, the chlorophylls are located in
(a) stroma
(b) lumen of grana
(c) outer membrane
(d) thylakoid membrane
Answer:
(d) thylakoid membrane

Question 4.
All algae generally have
(a) chlorophyll-a and chlorophyll-b
(b) chlorophyll-a and ß-carotene
(c) chlorophyll-b and ß-carotene
(d) phycoerythrin and ß-carotene
Answer:
(a) chlorophyll-a and chlorophyll-b

Question 5.
In C₄ -plants, the first stable product of CO₂-fixation in mesophyll cells is
(a) 3-phosphoglycerate
(b) dihydroxyacetonephosphate
(c) oxaloacetate
(d) phosphoenol pyruvate
Answer:
(c) oxaloacetate

Question 6.
During light absorption and emission by chlorophyll molecule, the length of fluroscent light is
(a) longer than that of absorbed light
(b) shorter than that of absorbed light
(c) equal to that absorbed light
(d) equal to that of phosphorescent light
Answer:
(a) longer than that of absorbed light

Question 7.
Electron donor to PS-I is
(a) cyt-b
(b) cyt-b₆
(c) ferredoxin
(d) plastocyanin
Answer:
(d) plastocyanin

Question 8.
The reaction centre of PS-II is:
(a) P₆₀₀
(b) P₆₈₀
(c) P₇₀₀
(d) P₇₅₀
Answer:
(b) P₆₈₀

Question 9.
The ions essential for photolysis of water during photosynthesis are
(a) Mn⁺⁺, Ca⁺⁺ and Cl^–
(b) Mg⁺⁺, Ca⁺⁺ and Cl^–
(c) Cu⁺⁺, Ca⁺⁺ and Mg⁺⁺
(d) Fe⁺⁺, Ca⁺⁺ and Mn⁺⁺
Answer:
(a) Mn⁺⁺, Ca⁺⁺ and Cl^–

Question 10.
The fist reaction of photosynthesis is
(a) excitation of chlorophyll
(b) photolysis of water
(c) ATP formation
(d) CO₂-fixation
Answer:
(a) excitation of chlorophyll

Fill in the blanks

Question 1.
The graph showing the effectiveness of different wave lengths of light on the photosynthetic activity of leaves is known as …………… .
Answer:
Action spectrum

Question 2.
In higher plants the reaction centre chlorophyll of PS-I is …………. .
Answer:
P₇₀₀

Question 3.
In C4-plants Rubisco is present is the chloroplasts of ………….. cells.
Answer:
Spongy

Question 4.
The accepter of CO₂ during photosynthesis in bundle sheath cells of C4-plants is …………….. .
Answer:
RuBP. (Ribulose-1, 5 biphosphate)

Question 5.
Kranz type of leaf anatomy is seen in ………….. plants.
Answer:
C₄

Short Answer Type Questions

Question 1.
Absorption spectrum
It is the curve that shows the amount of different wavelength of lights absorbed by a substance (photosynthetic pigment). The graph given below shows the ability of chlorophyll-a to absorb lights of different wavelengths.
Chlorophyll-a shows the maximum absorption peak at 450 nm and also shows another peak at 650 nm.

Graph showing the absorption spectrum, of chlorophyll-a, b, and the carotenoids

Question 2.
Photosystem
Answer:
During the course of light reaction, light is absorbed by photosynthetic pigments present in the quantasomes of grana thylakoids.
These photosynthetic pigments are organised into two discrete photochemical Light Harvesting Complexes (LHCs) known as Photosystem-I (PS-I) and Photosystem-II (PS-II).
The light harvesting complexes or photosystems are made up of hundreds of pigment molecules bounded by proteins. Each photosystem has a photocentre or reaction centre, where actual reaction takes place.

Question 3.
Photolysis of water
Answer:
The electrons are continuously supplied to the photosystems-II by the available electrons, which get replaced due to the splitting of water.
In this process, the water splits into protons, electrons and oxygen. The complex for water splitting is associated with the photosystems-II that is located on the inner side of the thylakoid membrane. Mn+ and Cl- ions also play important role in the photolysis of water molecule. These electrons thus, obtained by the splitting of water are needed to replace those electrons which are removed from the photosytems-I thus, are provided by photosystem-II.
2H₂O → 4H⁺ + O₂ ↑ + 4e^–
While all the electrons formed, are replaced, the protons get accumulated in the lumen of the thylakoid and the oxygen is evolved into the atmosphere.

Question 4.
Photophosphorylation
Answer:
Phosphorylation is the process through which, ATP is synthesised from ADP and inorganic phosphate (P) by the cell organelles (like mitochondria and chloroplasts). When it occurs in the presence of sunlight in chloroplast, it is called photophosphorylation.

Phosphorylation in mitochondria is not light dependent, but it uses the energy by oxidation of nutrients to produce ATP, hence it is called oxidative phosphorylation.

Question 5.
Photorespiration
Answer:
It is a light dependent cyclic process of oxygenation of RuBP and release of carbon dioxide by the photosynthetic organs of a plant. The site of photorespiration is chloroplast. Mitochondria and peroxisome are also required for completing the process. RuBP carboxylase, oxygenase is the main enzyme of dark reaction. It also catalyses another reactions that interferes with the functioning of Calvin cycle. It has active site for both, i.e. CO₂ and O₂.

The relative concentration of CO₂ and O₂ determines which of the two will bind to the enzyme.
Under the conditions, when O₂ concentration is more in atmosphere than CO₂, C₃-plants, RuBisCO acts as oxygenase enzyme and CO₂-fixation does not lead to PGA formation. Instead phosphoglycerate and phosphoglycolate are formed and photorespiration occurs.

Question 6.
CAM plants
Answer:
Some plants belonging to family-Crassulaceae have special kind of adaptation for performing photosynthesis. These are succulent photosynthetic xerophytic plants. These plants keep their stomata open during night and fix CO₂ in the night and use it in the day time. This is a xerophytic adaptation of plants to reduce transpiration rate by keeping stomata shut during day time. The events of this process are summarised in the flow chart given below

Long Answer Type Questions

Question 1.
Describe the light reaction of photosynthesis.
Answer:
5 Light Reaction (The Photochemical Phase)
Light reaction includes the following steps, i.e. absorption of light, splitting of water, release of oxygen and finally the formation of high energy chemical intermediates, i.e. ATP and NADPH.

Light Absorption
During the course of light reaction, light is absorbed by photosynthetic pigments present in the quantasomes of grana thylakoids.
These photosynthetic pigments are organised into two discrete photochemical Light Harvesting Complexes (LHCs) known as Photosystem-I (PS-I) and Photosystem-II (PS-II).

The light harvesting complexes or photosystems are made up of hundreds of pigment molecules bounded by proteins. Each photosystem has a photocentre or reaction centre, where actual reaction takes place.

This reaction centre contains a special chlorophyll-a molecule. It is fed by hundred other pigment molecules and it forms the light harvesting system called antennae. These antennae molecule absorb light of different wavelength, but shorter than reaction centre in order to make photosynthesis more efficient.

The light harvasting complex

The reaction centre is different in both the photosystem as given below
(i) In PS-I, the reaction centre or chlorophyll-a has peak of absorption at 700 nm, known as P₇₀₀.
(ii) In PS-II, the reaction centre has absorption peak at 680 nm hence, called P₆₈₀.

Question 2.
Explain different phases of Calvin cycle.
Answer:
The C₃ Cycle
This is a cyclic biochemical pathway of reduction of CO₂ or photosynthetic carbon, which was discovered by Calvin.
The Calvin cycle runs in all photosynthetic plants, no matter they show C₃, C₄ or any other pathway. It occurs in stroma of the chloroplast.

Primary Acceptor of CO₂ in C₃ Pathway
After a long research and conducting many experiments it was concluded by the scientists that in C₃ pathway, the acceptor molecule is a 5-carbon ketose sugar, i.e. Ribulose 5-Bisphosphate (5 RuBP). Calvin or C₃ cycle has many steps which are known as glycotic reversal or formation of sugar and takes place between reduction and regeneration. There are three major steps as follows

1. Carboxylation
It is the most crucial step of the Calvin cycle. In this fixation of CO₂ molecule takes place in the form of carboxylation of RuBP(5C). This reaction is catalysed by the enzyme RuBP carboxyase. This finally leads to the formation of two molecules of 3 Phosphoglyceric Acid (3PGA). As the RuBP carboxylase enzyme also has an activity of oxygenation. Thus, it is more commonly known as RuBP carboxylase-oxygenase or RuBisCO.
Img 5
Diagrammatic representation of Calvin cycle, regeneration of RuBP is indicated by broken lines

2. Reduction
After the carboxylation reaction, reduction of PGA takes place through a series of reactions leading to the formation of glucose.
In this step, the ATP (as energy source) and NADPH (hydrogen atom carrier) are utilised.
It is to be noted that 2 molecules of ATP and 2 molecules of NADPH are utilised in this step for phosphorylation and for the reduction of CO₂, respectively.
Hence, the fixation of 6 molecules of CO₂ and 6 turns of the cycle are required in order to release one molecule of glucose from the pathway.

3. Regeneration
For the continuous and uninterrupted functioning of the Calvin cycle, there must be a regular supply of ATP, NADPH and also sufficient amount of RuBP is required. The regeneration of RuBP (CO₂ acceptor) is a complex process and involves many types of sugar starting from triose (3C) to heptose (7C).
The regeneration step requires one ATP molecule for phosphorylation. Hence, for every CO₂ molecule that enters the Calvin cycle are required 3 molecules of ATP and 2 molecules of NADPH.

Thus, in order to produce one molecule of glucose through the Calvin pathway, 18 ATPs and 12 NADPHs are required.

Question 3.
Explain different phases of C4 pathway.
Answer:
The C₄ Pathway
It was worked out by two Australian scientists Hatch and Slack (1966). Thus, this is also known as Hatch and Slack pathway. C₄-plants are special as they have a special type of leaf anatomy that can tolerate high temperatures and show a response to high intensities. Inspite of having Oxaloacetic Acid (OAA) as their first CO₂ -fixation product, they use C₃ pathway or the Calvin cycle as the main photosynthetic pathway.

Note:

• Only angiospermic (no gymnosperm, bryophytes and pteridophytes, etc.) plants show this process to fix CO₂.
• The main aim of C₄-cycle is to fix very dilute solution of CO₂ (0.03% or 300 ppm) to concentrated CO₂ solution in bundle sheath cells to produce Oxaloacetic Acid (OAA).

Kranz Anatomy:
According to the structural leaf anatomy of C₃ and C₄-plants, the leaves of C₃-plants show only one type of cells called mesophyll cells, which contain only mesophyll chloroplast, while leaves of C₄-plants show two types of cells, i.e., outer mesophyll cells and inner spongy (which are large) cells around the vascular bundles called bundle sheath cells arranged in a circular manner.

It refers to the presence of two types of the chloroplast, in the leaves. The mesophyll cells contain well-developed granal chloroplast. They actively participate in light reaction. These produce ATP and NADPH₂.

The rudimentary chloroplasts are present in the cells of bundle sheath. They are agranal. The bundle sheath cells are mainly meant to carryout C₃ cycle.
This does not require well-developed chloroplast, so they are rudimentary lamellar type.

TS of maize leaf showing Kranz anatomy

The bundle sheath cells tend to form several layers around the vascular bundles.

They possess several special features such as

• Have large number of chloroplast.
• Thick walls which are impervious to gaseous exchange.
• There are no intercellular spaces.
  The Hatch and Slack pathway is also a cyclic process, which occurs in following steps

Step I: In C₄-plants, the initial fixation of CO₂ occurs in mesophyll cells. The primary acceptor of CO₂ is Phosphoenol Pyruvate (PEP).
Step II: It combines with CO₂ in the presence of an enzyme phosphoenol pyruvate carboxyfcise or PEP carboxylase (PEPcase) to form the first stable (or a 4 carbon organic acid) product of C₄ pathway, i.e. the Oxaloacetic Acid (OAA).
Step III: The compound (OAA) are transported to the bundle sheath cells where they are broken down, releasing CO₂ and a 3-carbon molecule.
Step IV: The 3-carbon compound is again transported back to the mesophyll cells where regeneration of PEP takes place, thus, completing the cycle.

Schematic representation of Hatch and Slack pathway

The CO₂ thus, released in the bundle sheath cells enters the C₃ or the Calvin cycle (common pathway to all plants).

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 12 Mineral Nutrition Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 12 Question Answer Mineral Nutrition

Mineral Nutrition Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Multiple Choices Questions

Question 1.
Most of the plants absorb nitrogen from soil in the form of.
(a) free N₂
(b) nitrites
(c) Nitrates
(d) NH₃
Answer:
(c) Nitrates

Question 2.
Choose the micro-nutrient
(a) Sulphur
(b) Manganese
(c) Calcium
(d) Nitrogen
Answer:
(b) Manganese

Question 3.
Choose the macronutrient
(a) Manganese
(b) Phosphorus
(c) Zinc
(d) Molybdanum
Answer:
(b) Phosphorus

Question 4.
Symbiotic nitrogen fixation is done by
(a) Rhizobium
(b) Clostridium
(c) Nostoc
(d) Azotobacter
Answer:
(a) Rhizobium

Question 5.
The enzyme responsible for nitrogen fixation requires.
(a) Fe and Mo
(b) Mo and Ca
(c) Zn and Cu
(d) Zn and Mn
Answer:
(a) Fe and Mo

Question 6.
Micro-organisms affect fertility of soil by
(a) Nitrogen-fixation
(b) Production of toxins
(c) Destroying harmful bacteria
(d) Retaining moisture
Answer:
(a) Nitrogen-fixation

Question 7.
Maintenance of soil fertility without addition of nutrients is due to
(a) activity of micro-organisms
(b) floods
(c) favourable temperature
(d) standing crops
Answer:
(a) activity of micro-organisms

Question 8.
The root nodules formed in the leguminous plant have a red pigment called
(a) Hemoglobin
(b) Phycocyanin
(c) Leghemoglobin
(d) Chlorophyll
Answer:
(c) Leghemoglobin

Question 9.
The process of conversion of ammonia into nitrate is called.
(a) Nitrification
(b) Ammonification
(c) Transcription
(d) Translation
Answer:
(a) Nitrification

Question 10.
The enzyme responsible for fixing nitrogen is called.
(a) Nitrate reductase
(b) Nitrite reductase
(c) Nitrogenase
(d) Aminoacid synthetase
Answer:
(c) Nitrogenase

Short Answer Type Questions

Write short notes on

Question 1.
Essential elements
Answer:
Essential. Mineral. Nutrients (Elements):
Essential elements are those elements which possess rhcir own structural or physiological properties and also without which the plants arc unable to complete their life cycle.
Plants has the ability to absorb most of the minerals present in the soil. More than sixty minerals present in soil have been recorded essential for plants our of the 105 discovered so far.

Question 2.
Hydroponics
Answer:
Hydroponics or Soilless Culture:
The technique of hydroponic was demonstrated by the experiment conducted by Julius Von Sach. It explains that the plants can be grown co their level of maturity in a well-defined nutrient solution even in the absence of soil.
Thus this technique of growing plant in a nutrient solution without soil is well-known and is also called water culture.

Question 3.
Biological nitrogen-fixation
Answer:
Biological Nitrogen-Fixation
The process in which atmospheric nitrogen gets converted into inorganic nitrogenous compounds (nitrate, nitrite and ammonia) by the involvement of microorganisms (bacteria, cyanobacteria, etc) is called biological nitrogen-fixation.
Very few organisms can utilise atmospheric nitrogen, only certain prokaryotes are capable of fixing nitrogen. The prokaryotic organism that reduces nitrogen has an enzyme called nitrogenase. Such microbes are called N₂ -fixers.
Img 1
Biological nitrogen-fixation may occur in asymbiotic as well as symbiotic manner.

Question 4.
Macronutrients
Answer:
Macronutrients
The elements that are generally found in plant tissues in large or excess amounts (around 10 m mole kg-1 or 10 mg per gram of dry matter) are called macronutrients or major elements. These elements are generally involved in the synthesis of organic molecules and development of osmotic potential. The list of macronutrients includes carbon, hydrogen, oxygen, nitrogen, phosphorus, sulphur, potassium, calcium and magnesium.
Out of all these elements, carbon, hydrogen and oxygen are obtained from CO₂ and H₂O while, the other elements are obtained from the soil itself.

Question 5.
Micronutrients
Answer:
Micronutrients:
The elements that are generally found in traces or very small amount only (i.e., less than 10 m mole kg-1 or less than 0.1 mg per gram of dry matter) are called micronutrients or minor elements. These are generally eight in number and the list includes iron, manganese, copper, molybdenum, zinc, boron, chlorine and nickel. These are mosdy involved in the functioning of enzymes as cofactors or activators of metals.

Question 6.
Asymbiotic nitrogen-fixation
Answer:
Asymbiotic Nitrogen-Fixation:
The fixation of N₂ by the microorganisms living freely, i.e. outside the plant cell is called asymbiotic or non-symbiotic biological nitrogen-fixation.
JE Carnahan in 1960 first reported the conversion of atmospheric nitrogen into ammonia by the asymbiotic or free-living nitrogen-fixing bacteria Clostridium pasteuriansums.

Question 7.
Symbiotic nitrogen-fixation
Answer:
It is the process of nitrogen-fixation with the help of symbiotic microorganisms. It involves a symbiotic relationship between plant and concerned microorganism. The process of symbiosis involves two organisms living together in different associations. Several types of biological nitrogen-fixing associations are known.
The most familiar one is the relationship of Rhizobium with the roots of several legumes belonging to class-Leguminosae like sweet pea, lentils, garden pea, alfalfa, sweet clover, broad bean, clover beans, etc.

Question 8.
Leghemoglobin
Answer:
Leghaemoglobin It is the red pigment found in the root nodules of leguminous plants. This reddish pigment is found in the cytoplasm of host cells. Leghaemoglobin combines with O₂ and helps to protect nitrogenase from O₂ damage. It also maintains steady supply of O₂ to nitrogen fixing bacteria for respiration. The ATP generated in this process of bacterial respiration is used for N₂-fixation.

Differentiate Between

Question 1.
Macro-elements and microelements.
Answer:
The differences between macronutrients and micronutrients

Macronutrients	Micronutrients
Their quantities can be easily detected in plants as they occur in large amounts.	Their quantities are not easily detectable. They occur in very^ small amounts in plants.
These are needed for growth, metabolism and other body functions.	These nutrients help in detoxifying the body and warding of harmful diseases.
Play significant role in the development of osmotic potential.	Do not have any role in osmotic potential.
Their higher concentration do not cause toxicity.	They cause toxicity even with slight increase from their , . maximal range.
Compounds of macronutrients contain calories.	Compounds of micronutrients do not contain calories.
Their required concentration is atleast 1 mg/g of dry matter.	Their required concentration is equal to or less than 0.1 mg/g of dry matter.
e.g., proteins, carbohydrates and fats.	e.g., vitamins and minerals.

Question 2.
Symbiotic and asymbiotic nitrogen-fixation.
Answer:
The differences between symbiotic and asymbiotic fixation

Symbiotic fixation	Asymbiotic fixation
Fixation of N<sub>2</sub> by symbiotic microorganisms.	Fixation of N<sub>2</sub> by free-living microorganisms.
Microorganisms involved are Clostridium, Azotobacter, etc.	Microorganism involved is Rhizobium.

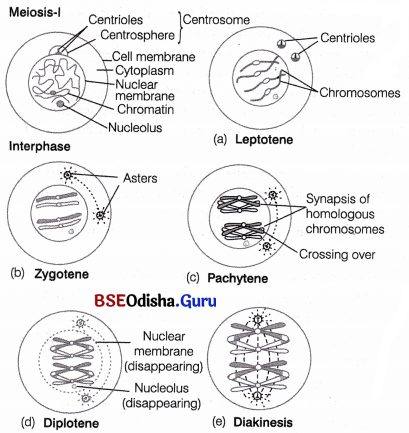
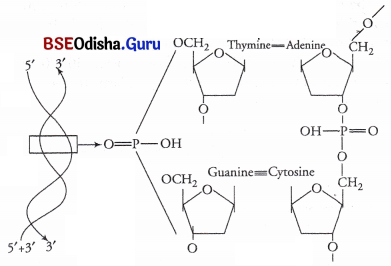
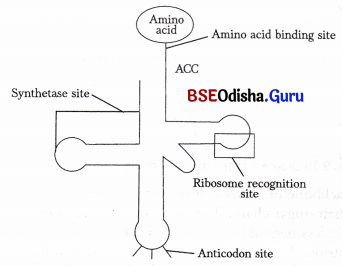
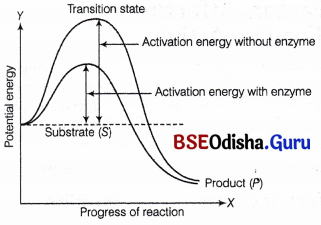
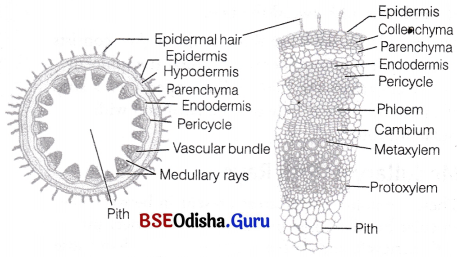
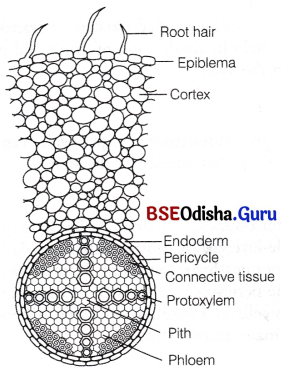
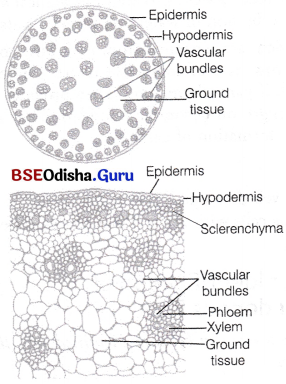
Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 11 Transport in Plants Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 11 Question Answer Transport in Plants

Transport in Plants Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Choose the correct answer

Question 1.
When a cell becomes fully turgid being kept in water for sometime, which of its osmotic components becomes zero?
(a) OP
(b) TP
(c) Osmotic potential
(d) Pressure potential
Answer:
(b) TP

Question 2.
When a cell becomes flaccid being kept in a solution for sometime, then
(a) Pressure potential = zero
(b) Osmotic potential = zero
(c) Water potential = Pressure potential
(d) Pressure potential = Osmotic potential
Answer:
(a) Pressure potential = zero

Question 3.
When sucrose is dissolved in water, its water potential
(a) increases
(b) decreases
(c) becomes zero
(d) is not affected
Answer:
(b) decreases

Question 4.
If a cell is placed in hypertonic solution, what will happen?
(a) Endosmosis
(b) Exosmosis
(c) Deplasmolysis
(d) None of these
Answer:
(b) Exosmosis

Question 5.
If a cell volume decreases when placed in 0. 254 M sucrose solution, then the cell sap concentration is
(a) Equal to 0.25 M
(b) Less than 0.25 M
(c) More than 0.25 M
(d) Unpredictable
Answer:
(b) Less than 0.25 M

Question 6.
Root pressure is maximum when
(a) Absorption of water is high and rate of % transpiration is high
(b) Absorption of water is low and rate of transpiration is low
(c) Absorption of water is high and rate of transpiration is low
(d) Absorption of water is low and rate of transpiration is high
Answer:
(c) Absorption of water is high and rate of transpiration is low

Question 7.
When starch is converted to glucose in guard cells, their water potential
(a) increases
(b) decreases
(c) becomes zero
(d) is not affected
Answer:
(b) decreases

Question 8.
Ascent of sap in plants takes place through
(a) xylem
(b) phloem
(c) cambium
(d) Both xylem and cambium
Answer:
(b) xylem

Question 9.
Ascent of sap in tall tree is best explained by
(a) root pressure
(b) cohesion-tension theory
(c) capillary force
(d) imbibition
Answer:
(b) cohesion-tension theory

Question 10.
Which one is associated with stomatal regulation in plants?
(a) K⁺
(b) Na⁺
(c) Mg⁺
(d) PO^–₄
Answer:
(a) K+

Fill in the blanks

Question 1.
Stomata opens when guard cells become ……………. .
Answer:
turgid

Question 2.
Water potential of leaves are ………….. than that of roots during active transpiration.
Answer:
lower

Question 3.
Cohesion-tension theory of ascent of sap was proposed by …………… .
Answer:
Dixon and Jolly

Question 4.
The water coming out through hydathode contains ……………. .
Answer:
organic and inorganic salts

Question 5.
Pulsation theory of ascent of sap was advocated by ………………… .
Answer:
Sir JC Bose

Question 6.
In a flaccid cell, ψ = …………… .
Answer:
Solute potential

Question 7.
Water potential of pure water is taken as ……………… .
Answer:
zero

Question 8.
The density of a substance (d) is related to its rate of diffusion (r) by the relation, r = …………. .
Answer:
r = \(\frac{1}{\sqrt{4d}}\)

Question 9.
A plant cell placed in water reaches its maximum volume when its ψ_s =
Answer:
0

Question 10.
If ψ_s of a solution kept in a beaker is – 0.5 MPa, then its ψ =
Answer:
-0.5

Short Answer Type Questions

Question 1.
Symplast
Answer:
This system includes the living part of the plant cells made up of interconnected protoplasts’of neighbouring cells and connected through cytoplasmic strands extending through plasmodesmata.

The water that enters into the cell sap of root hair as a result of active absorption, moves into the underlying cortex cells bounded by a continuous selectively permeable membrane through plasmodesmata.

The movement in this pathway is relatively slower (as, water enters the cells through the cell membrane). The movement is again down the potential gradient and is aided by cytoplasmic streaming, which helps in quicker movement across individual cells. Thus, facilitating the transport.

It is generally believed that both apoplast and symplast v pathways are operative in plants, but apoplast pathway offers less or no resistance. Thus, water continues to move through apoplast in the roots.

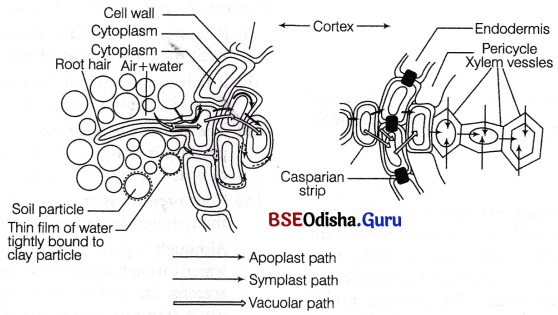
Question 2.
Apoplast
Answer:
Apoplast is the system of adjacent cell walls (i.e., interconnecting cell walls, intercellular spaces, cell wall of endodermis) that occurs continuously throughout the plant, except at the casparian strips of endodermis in roots. In this pathway, the movement of water molecules takes place through intercellular spaces and the walls of cells only.

The water movement takes place along the gradient from root hairs to xylem through the walls of intervening cells without crossing any membrane or cytoplasm.Thus, it does not provide any barrier to the movement of water, which occurs through mass flow due to adhesion and cohesion of water molecules. There is no involvement of osmosis in the apoplast pathway.

Question 3.
Root pressure
Answer:
It is believed that all plants absorb excess of water by an active process and tends to build up a positive hydrostatic pressure within the root system called root pressure. Due to this activity, the water is pushed upward along the length of the stem to a small height. The pressure inside the xylem is caused due to diffusion pressure gradient and is maintained by the activity of living cells.

Question 4.
Transpirational pull
Answer:
Plants themselves have a continuous water column in their xylem channels that starts at the base, (i.e. roots) and continues upto leaves from where water is lost through the process of transpiration. Thus, despite the absence of a circulatory system in plants, the flow of water upward through the xylem in plants achieves fairly high rates i.e. upto 15 metres per hour.

The water molecules in the water column remain attracted by the cohesive force and cannot be separated easily from one another. Thus, there is attraction between water molecules and the inner wall of xylem ducts due to which the water column cannot be pulled away from the walls of xylem ducts due to strong adhesive and cohesive forces. Hence, maintaining the continuity of water column from roots to leaves.

Water is lost from mesophyll cells to the intercellular spaces as a result of transpiration which develops a strong negative water potential. There are very large number of leaves and each leaf has thousands of transpiring mesophyll cells, which withdraws water from the xylem. This leads to a negative pressure in the water column, which exerts an upward pull over the water column. The xylem elements of roots) now moves upward under the influence of transpirational pull.

Thus, the cohesive, adhesive forces and transpiration pull all together help in lifting up of water through xylem elements and because of the critical role of cohesion the transpiration pull is also called cohesion-tension transpiration pull model of water transport.

Question 5.
Mechanics of stomatal opening
Answer:
Opening of Stomata
During this phenomenon, turgidity within guard cells increases due to endosmosis flanking each stomatal aperture or pore. Then, the thin outer walls stretch and bulge out. Pulling apart the opposite inner thick walls from each other (inner walls form a crescent shape) thereby, creating a pore or an opening in guard cells of stomata. Hence, making stomata to get open.

Question 6.
Significance of transpiration
Answer:
Transpiration is necessary and vital process. Various advantages are given below

1. Helps in maintaining shape and structure of the plants by keeping cells turgid.
2. It helps in regulation of temperature and cooling effect, i.e. cool leaf surfaces upto 10-15°C sometimes by evaporative cooling.
3. It helps in supplying water for the process of photosynthesis.
4. Helps in ascent of sap, (i.e. creates transpiration pull for absorption and transport of plants).

Question 7.
Hydathode
Answer:
Hydathodes A hydathode is an opening along the leaf margin that is able to release water. Hydathodes are absent from the rhizome, from the part of stem invested by leaves and from the inner surfaces of leaf sheaths, but they are found in all other aerial parts except the flower. Hydathodes release water in a process called guttation.

Question 8.
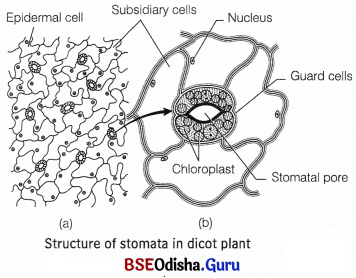
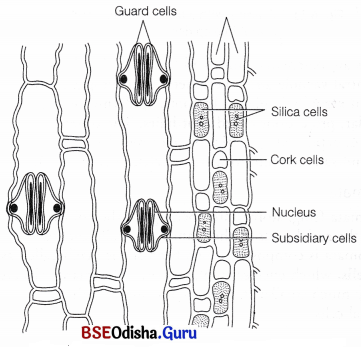
Stomata
Answer:
It is already known that plants do not utilise the total amount of water absorbed by them, out of total 100% of water, only 5-10% is utilised. Rest 90-95% of water is lost through transpiration from the aerial parts of plants (mainly from leaves) in the form of water vapours. The process of transpiration is carried out by the special structures found in leaves of plants called stomata.

Question 9.
Diffusion
Answer:
It is a physical process in which different solvent molecules or solute ions are transported passively without the expenditure of energy. It is a slow process and is independent of living system. During this process, the molecules or ions (be it a gas, liquid or solids) flow in a random fashion from the region of higher concentration to region of lower concentration.
Rate of diffusion is mainly affected by the following factors

• Concentration gradient of diffusing substance.
• Permeability of the membrane separating them.
• Temperature
• Pressure
• Density

Diffusion process is an important phenomenon in plants as it is the only means of transport of gases and materials in them.

Question 10.
Imbibition
Answer:
It is a special type of diffusion in which water is adsorbed by the solid particles (colloids) of a substance. The water molecules get tightly adsorbed at the surface of molecules/substances and become immobilised. This leads them to increase enormously in volume.
The solid particles which imbibe water or any other liquid are called imbibants. While, the liquid, which is imbibed is known as imbibate. The process of imbibition is also known as a type of diffusion because in this the movement of water occurs along the concentration gradient.
Imbibition can be best explained and seen in absorption of water by seeds and dry wood which act as absorbents to imbibe water and swell.

Question 11.
Water potential
Answer:
All living organisms require energy for their growth, to maintain metabolism and to reproduce. As water molecules possess kinetic energy, they are always in random motion (in both liquid and gaseous form) which is rapid and constant.
Water potential is the difference between the free energy of water molecules in pure water and the energy of water in any other system. It is denoted by \j/(psi) and expressed in pressure unit i.e. pascals (Pa).

Question 12.
DPD
Answer:
Diffusion Pressure Deficit (DPD) or Suction Pressure (SP)
The term ‘Diffusion Pressure Deficit’ (DPD) was coined by BS Meyer in 1938. The amount by which diffusion pressure of a solution is lower than that of its pure solvent is known as diffusion pressure deficit.
DPD = OP – TP
Fully turgid cell OP = TP
DPD = O
Fully flaccid cell TP = O
DPD = OP
The DPD of any cell is the measure of water absorbing capacity of that cell. It is also called as suction pressure. Thus, suction pressure is a measure of the ability of a cell to absorb water.

Question 13.
Turgor pressure
Answer:
It is the hydrostatic pressure exerted by the cell contents against the cell wall due to the osmotic entry of water. It is variable as TP is maximum when the cell is fully turgid, and is zero when the cell is flaccid.
In a turgid cell, the walls of cell exert an equal and opposite pressure in response to Turgor Pressure (TP).
This is called as Wall Pressure (WP). So, TP = WP.

Long Answer Type Questions

Question 1.
Describe the mechanism of water absorption by plant roots.
Answer:
Mechanism of Water Absorption
It takes place by two methods
1. Active Absorption of Water
Two theories have been put forward to explain active absorption of water these are
(i) Osmotic Theory According to this theory, water moves from soil to root hairs by means of diffusion along a gradient of decreasing water potential (ψ). Root hair cells and xylem sap has lower water potential than the soil solution. So, water moves from soil to the root xylem by cell to cell osmosis.

(ii) Non-osmotic Theory According to this theory, water is absorbed by the root cells even if the soil water potential is lower than the cell sap. It is supported by the following facts

• There exist a relation between rate of respiration and absorption of water.
• Factors affecting rate of respiration also affect absorption of water.
• There exists an auxin induced water uptake.

2. Passive Absorption of Water
According to this theory, the main driving force for water absorption is the transpiration pull.
This pulls water from soil through root hairs and then from xylem column of roots and stems.
Water in plants is considered as continuous hydraulic system, connecting water in soil and water vapours in the atmosphere surrounding the plants.

In the passive absorption of water, the rate of absorption of water by plants is approximately equal to the rate of transpiration, provided water is available in optimum quantity .in the soil.

In general, all plants absorb water through roots. However, the area of young roots where most absorption of water and minerals takes place is called the root hair zone. The root hairs are thin-walled, slender extension of root epidermal cell found at the tip of roots in millions. These are very delicate structures, which do not last for more than days or a week. They also have very sticky walls that help in tight adhesion to the soil particles.

Question 2.
Describe the factors affecting water absorption by plant roots.
Answer:
Factors Affecting Absorption of Water
The rate of absorption of water is affected by
1. External environmental factors like soil, temperature, soil aeration, concentration of soil solution and availability of water in the soil, affect the rate of absorption of water.
2. Internal factors include metabolism of root system, (including number of root hairs, etc.) and the rate of transpiration.

Question 3.
Describe the transpirational pull and cohesion-tension theory of ascent of sap.
Answer:
Transpiration Pull and Cohesion-Tension Theory
Plants themselves have a continuous water column in their xylem channels that starts at the base, (i.e. roots) and continues upto leaves from where water is lost through the process of transpiration. Thus, despite the absence of a circulatory system in plants, the flow of water upward through the xylem in plants achieves fairly high rates i.e. upto 15 metres per hour.

The water molecules in the water column remain attracted by the cohesive force and cannot be separated easily from one another. Thus, there is attraction between water molecules and the inner wall of xylem ducts due to which the water column cannot be pulled away from the walls of xylem ducts due to strong adhesive and cohesive !* forces. Hence, maintaining the continuity of water column from roots to leaves.

Water is lost from mesophyll cells to the intercellular spaces as a result of transpiration which develops a strong negative water potential. There are very large number of leaves and each leaf has thousands of transpiring mesophyll cells, which withdraws water from the xylem. This leads to a negative pressure in the water column, which exerts an upward pull over the water column. The xylem elements of roots) now moves upward under the influence of transpirational pull.

Thus, the cohesive, adhesive forces and transpiration pull all together help in lifting up of water through xylem elements and because of the critical role of cohesion the transpiration pull is also called cohesion-tension transpiration pull model of water transport.

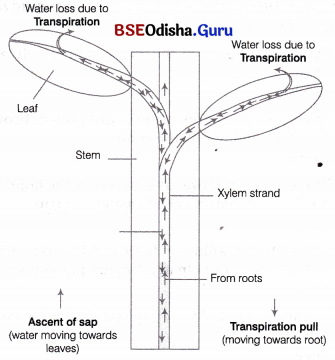
Transpiration pull (tension) and ascent of sap

Question 4.
Write how potassium ions regulate the opening and closing of stomatal pore.
Answer:
Malate or K⁺ Ion Pump Theory
The main features of this theory were put forward by Levitt (1974). This is also known as modern theory. According to this, there is accumulation of K+ ions in the guard cells during stomatal opening. And the influx of K+ into the guard cells is accompained by the synthesis of malic acid (an organic acid).
Differences occurring during day and night
Tablee

Question 5.
Describe the factors affecting the transpiration in plants.
Answer:
Factors Affecting Transpiration
There are several external and internal factors that affect the rate of transpiration in many ways.

Some of them are given below
(i) External Factors
These include the factors that influence the rate of transpiration (such as temperature, light, humidity and speed of wind).
(ii) Internal (Plant) Factors
These include the factors that are other than the physical factors such as number of stomata, distribution of stomata, per cent of open stomata, water status of plant and canopy structure.

Question 6.
What do you mean by water potential? Describe its components.
Answer:
Components of Water Potential
The water potential (ψ_w) of a living cell has three major components such as solute potential (ψ_s) or osmotic potential, pressure potential (ψ_p) and matric potential (ψ_m). Water potential is actually the sum of all above three potentials. N
Water potential ψ = ψ_m + ψ_s + ψ_p

1. Solute Potential
The amount by which the water potential is reduced as a result of the presence of a solute in pure water is known as solute potential. It is also known as osmotic potential.

Solute potential is denoted by ψ_s and are always in negative values (or has value less than zero). Hence,
More number of solute molecules
= Lower solute potential (more — ve).
At atmospheric pressure for a solution,
ψ_w(Water potential) = ψ_s(Solute potential)

2. Pressure Potential
If a pressure more than atmospheric pressure is applied to pure water or a solution containing solute, the water potential increases. This is equal to pumping water from one place to another, e.g. our heart build up pressure for the circulation of blood in the body.

When water enters a plant cell through diffusion, it becomes turgid due to building up of pressure against the cell wall in a plant system. This leads to increase in the pressure potential. It is usually positive in nature and hence, known as a turgor pressure (denoted by ψ_p). Loss of water during transpiration produces a negative hydrostatic pressure or tension in the; xylem. This is very important in transport (ascent of sap) over long distances in plants. The water potential of any systems is thus, affected by both solute and pressure potential.
i.e., ψ_w = ψ_s + ψ_p

3. Matric Potential(ψ_m)
It is a component of water potential due to the adhesion of water molecules to non-dissolved structures of the system, i.e. the matrix, such as plasma membranes. It is represented by ψ_m. It is always negative and is significant only outside living cells in relatively dry system, e.g. soils.

Question 7.
Describe the relationship between DPD, OP and TP of a cell.
Answer:
The term ‘Diffusion Pressure Deficit’ (DPD) was coined by BS Meyer in 1938. The amount by which diffusion pressure of a solution is lower than that of its pure solvent is known as diffusion pressure deficit.
DPD = OP – TP
Fully turgid cell OP = TP
DPD = O
Fully flaccid cell TP = O
DPD = OP
The DPD of any cell is the measure of water absorbing capacity of that cell. It is also called as suction pressure. Thus, suction pressure is a measure of the ability of a cell to absorb water.

Question 8.
Give an account of diffusion.
Answer:
It is a physical process in which different solvent molecules or solute ions are transported passively without the expenditure of energy. It is a slow process and is independent of living system. During this process, the molecules or ions (be it a gas, liquid or solids) flow in a random fashion from the region of higher concentration to region of lower concentration.
Rate of diffusion is mainly affected by the following factors

• Concentration gradient of diffusing substance.
• Permeability of the membrane separating them.
• Temperature
• Pressure
• Density

Diffusion process is an important phenomenon in plants as it is the only means of transport of gases and materials in them.

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 10 Cell Division Cycle Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 10 Question Answer Cell Division Cycle

Cell Division Cycle Cells Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Multiple choice questions

Question 1.
During cell division, the replication of DNA occurs during
(a) M-phase
(b) S-phaase
(c) G-phase
(d) Prophase
Answer:
(b) S-Phase

Question 2.
In male flowers, meiosis is seen in
(a) sepals
(b) androecium
(c) petals
(d) gynoecium
Answer:
(b) androecium

Question 3.
From every meiocyte the spores formed is (are)
(a) one
(b) two
(c) four
(d) eight
Answer:
(c) four

Express in one word

Question 4.
The pairing of homologous chromosome.
Answer:
Synapsis

Question 5.
The points of exchange of chromosome segments.
Answer:
Crossing over

Question 6.
The process of end of exchange of chromosomal segments.
Answer:
Terminalisation

Question 7.
The process of division of cytoplasm into two cells.
Answer:
Cytokinesis

Question 8.
Cells with multiple chromosome numbers.
Answer:
Polyploids

Fill in the blanks

Question 9.
………… can disrupt spindle fibre and is also used to induce polyploidy.
Answer:
Colchicine

Question 10.
During the chromosomes are aligned at the equatorial plate.
Answer:
Metaphase

Question 11.
Where the cells are not separated by cell walls and nuclei lie scattered are called condition.
Answer:
Coenocytic

Question 12.
In yeasts, the cells divide by ………….. .
Answer:
budding

Question 13.
During pachytene …………. chromosomes pair.
Answer:
homologous

Short Answer Type Question

Question 14.
Write short notes on

(a) Control of cell cycle
Answer:
The cell cycle is controlled by certain proteins at certain points in a cell cycle called check points. These proteins are called Cyclin-dependent protein kinases (Cdks) and cyclins.
A Cdk is infact an enzyme that adds negatively charged phosphate groups to other molecules through phosphorylation process. This signals the cell to enter the next stage of cell cycle. But, Cdks are dependent on cyclins for their activation.
Cyclins are activating proteins that bind to Cdks to form a cyclin-Cdk complex. The exit from a particular phase of cell cycle takes place when cyclin gets degraded thereby deactivating Cdks.

(b) Chromosomal pairing
Answer:
Chromosomal pairing It occurs during zygotene of Prophase-I during meiois. During this process, the homologous chromosomes pair by the process called synapsis and the connecting material is called synaptonemal complex. The chromosomal pairs are called bivalents.

(c) S-phase of cell cycle
Answer:
S (Synthesis)-phase It is the phase in which actual synthesis or replication of DNA takes place. The overall amount of DNA doubles per cell, but no increase in chromosome number takes place during this phase. Therefore, if the initial amount of DNA is 2C, it will become 4C at the end of S-phase.
In case of animal cell, during S-phase DNA replication begins inside the nucleus while, the duplication of centrioles takes place in the cytoplasm.

(d) Anaphase of mitosis
Answer:
It is known to be the shortest duration phase, i.e., only of 2-3 min and is also very simple stage. At the beginning of this phase, splitting of chromosomes (that are already arranged at metaphase plate) takes place.
The two daughter chromatids now become the chromosomes of future daughter nuclei and start migrating towards the opposite poles along the path of their chromosome fibres.

(e) Amitosis
Answer:
It refers to the type of division that operate differently from the pattern followed by mitosis for, e.g.
(i) In some algal and fungal forms there is direct division of the cell nuclei.
(ii) In some cases, there is free nuclear division in which the cells do not possess cell walls and several nuclei are found scattered in the cytoplasm of large cells. These cells are called coenocytic cells.
(iii) In yeast, the cells divide by budding. The protoplast of parent cell bulges out through which a daughter nuclei migrates later to form a daughter cell.

Long Answer Type Questions

Question 15.
Describe the prophase-I of meiosis with suitable diagrams. What is the significance of this type of divison?
Answer:
Prophase-I
It is considered to be the most complicated and prolonged phase as compared to the similar stage in mitosis.
This phase is further subdivided into five subphases on the basis of chromosomal behaviour, i.e., leptotene, zygotene, pachytene, diplotene and diakinesis.

(i) Leptotene (Thin thread)
It is known to be the very first stage of meiotic division following the interphase.
Following features are seen during this phase

• Chromosomes become gradually visible under light microscope.
• Centrioles start moving towards opposite ends or poles and each centriole develops astral rays.
• Each chromosome is attached to the nuclear envelope through the attachment plate at both of its ends.

Homologous Chromosomes:
There are two sets of chromosomes in a diploid cell which undergo meiosis. One set of chromosomes is contributed by the male parent i and the other by the female parent. There are always two similar chromosomes having the same size, shape and position of centromere. In some organisms, the chromosomes give beaded appearance due to the presence of chromomeres (swollen area).

(ii) Zygotene (Yoked thread)
This is the next substage that takes place after the completion of the previous one. This is also a short lived stage like leptotene.
Following changes are seen during this phase

1. Homologous chromosomes pair up. This pairing is done in such a way that the genes of the same character present on the two chromosomes lie exactly opposite to each other. This process of association is known as synapsis.
2. It is revealed from the electron micrographic studies that the formation of synaptonemal complex takes place by a pair of homologous chromosomes that show synapsis. The complex so formed, on account of synapsis forms a bivalent or a tetrad.

(iii) Pachytene (Thick thread)
This is the stage which immediately follows zygotene where the pair of chromosomes become twisted spirally around each other and cannot be distinguished separately. This stage is comparatively long lived as compared to the previous two stages.

Following changes are seen during this stage

• Bivalent chromosomes are clearly seen as tetrads.
• In this stage, sometimes exchange of genes or crossing over between the two non-sister chromatids of homologous chromosomes occurs at the points called recombination nodules, which appear at intervals, on synaptonemal complex. By the end of pachytene recombination gets completed leaving the chromosomes linked at the sites of crossing over.

In this process, exchange of genetic material takes place between the non-sister chromatids of two homologpus chromosomes. It finally leads to recombination of genetic material on the two chromosomes.

(iv) Diplotene (Doube thread)
It is the stage of longest duration of all.
Following changes are observed during this stage

• In this, the synaptonemal complex appears to get dissolved while, the chromatids of each tetrad remain clearly visible.
• Recombined homologous chromosomes of the bivalents get separated and form chiasmata (X-shaped structures).
• Chiasmata formation is necessary for the separation of homologous chromosome which have undergone the process of crossing over.

(v) Diakinesis (Double ending)
This is the final stage of meiotic prophase-I. Also known as terminalisation, due to the shifting of chiasmata towards the end of the chromosomes.
Following changes are observed during this stage

• Chromosomes become fully condensed.
• Nucleolus degenerates.
• Breakdown of nuclear envelope into vesicles occurs.
• Formation of meiotic spindle (as in mitosis) in order to prepare the homologous chromosomes for separation also occurs.
• Diakinesis phase represents the transition from prophase to metaphase of meiosis-I.
  

Question 16.
Give an account of different phases a somatic cell undergoes during division process.
Answer:
Mitosis (M Phase):
In this type of division, the chromosomes replicate themselves and get equally distributed into daughter nuclei, i.e., the chromosome number in the parental and progeny cell (diploid) becomes the same. Therefore, it is also known as equational division.

Mitosis is also known as somatic cell division because it always occurs in somatic cells. Mitotic cell division is seen in the diploid somatic cells in animals, whereas, in plants, mitotic division is seen in both haploid and diploid cells.

It is known to be the phase of actual cell division, which starts with the division of nucleus, followed by the separation of daughter chromosomes, i.e., karyokinesis and terminates with the cytoplasmic division, i. e., cytokinesis.

Karyokinesis:
It is further divided into four main substages, i.e., prophase, metaphase, anaphase and telophase.

1. Prophase:
This phase is known for the initiation of condensation of chromosomal material, which during the process of chromatin condensation becomes untangled, and finally the centriole (already duplicated during S-phase of interphase) begins to move towards the opposite poles of the animal cell.

For the suitability in study we can categorise prophase as
(i) Early Prophase
During this phase, condensation of chromosomal material takes place in order to form compact mitotic chromosomes that are composed of two chromatids which are attached together at centromere.

The most conspicuous change that takes place during prophase is the formation of mitotic spindle. The initiation of mitotic spindle assembly, the micro-tubules and the proteinaceous components of the cell cytoplasm helps in the completion of the process. The mitotic spindle is formed between the two pairs of centrioles that migrate towards the opposite poles of the cell.

(ii) Late Prophase
At the end of the prophase, i.e., during late prophase the nucleolus disintegrates gradually and the nuclear envelope disappears. This disappearance marks the end of the prophase.

Question 17.
What is the significance of mitosis? Give details of the phases in between two successive M-phases.
Answer:
Mitosis (M Phase):
In this type of division, the chromosomes replicate themselves and get equally distributed into daughter nuclei, i.e., the chromosome number in the parental and progeny cell (diploid) becomes the same. Therefore, it is also known as equational division.

Mitosis is also known as somatic cell division because it always occurs in somatic cells. Mitotic cell division is seen in the diploid somatic cells in animals, whereas, in plants, mitotic division is seen in both haploid and diploid cells.

It is known to be the phase of actual cell division, which starts with the division of nucleus, followed by the separation of daughter chromosomes, i.e., karyokinesis and terminates with the cytoplasmic division, i. e., cytokinesis.

Question 18.
Give major points of comparision between mitosis, and meosis.
Answer:
Differences between Mitosis and Meiosis

Mitosis	Meiosis
This division occurs in somatic cells.	It occurs in reproductive cells.
It is a single division.	It is a double division.
The daughter cells resemble each other as well as their mother cell.	The daughter cells neither resemble one another nor their mother cell.
Replication of chromosomes occurs before every mitotic division.	Replication of chromosomes occurs only once though meiosis is a double division.
Mitosis does not introduce variations.	Meiosis introduces variations.
Mitosis is required for growth, repair and healing.	Meiosis is involved in sexual reproduction.

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 9 Chemical Constituents of Living Cells Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 9 Question Answer Chemical Constituents of Living Cells

Chemical Constituents of Living Cells Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
The name enzyme was coined by
(a) Edward Buchner
(b) Arthuze Harden
(c) Fredrich Kunhe
(d) Names Summer
Answer:
(c) Fredrich Kunhe

Question 2.
The,first enzyme purified and crystalised.
(a) Urease
(b) Hexokinase
(c) Alcohol dehydeogenase
(d) Catalase
Answer:
(a) Urease

Question 3.
Chemically ribozyme is
(a) Protein
(b) RNA
(c) DNA
(d) Lipoprotein
Answer:
(b) RNA

Question 4.
Which of the following is known as fruit sugar?
(a) Glucose
(b) Fructose
(c) Sucrose
(d) Maltose
Answer:
(b) Fructose

Question 5.
Which of the following elements is not present in nitrogenous bases found in nucleic acids?
(a) Nitrogen
(b) Hydrogen
(c) Carbon
(d) Phosphorous
Answer:
(d) Phosphorous

Question 6.
A nucleoside is a compound of
(a) N – base + sugar + phosphate
(b) N – base + sugar
(c) N – base + phosphate
(d) sugar + phosphate
Answer:
(b) N – base + sugar

Question 7.
Maltose is a disaccharide composed of
(a) D-glucose and D-glucose
(b) D-galactose and D-glucose
(c) D-glucose and D-fructose
(d) D-glucose and L-glucose
Answer:
(a) D-glucose and D-glucose

Question 8.
Which of the following is a sulphur containing amino acids?
(a) Methionine
(b) Serine
(c) Valine
(d) Leucine
Answer:
(a) Methionine

Question 9.
Name the hydroxy amino acid from the followings.
(a) Threonine
(b) Tryptophan
(c) Phenyl alanin
(d) Valine
Answer:
(a) Threonine

Question 10.
Which one of the followings is a basic amino acid?
(a) Lysine
(b) Glycine
(c) Tryptophan
(d) Leucine
Answer:
(a) Lysine

Question 11.
Which one of the followings is an ectodermal protein?
(a) Keratin
(b) Antibodies
(c) Storage proteins
(d) Enzymes
Answer:
(a) Keratin

Fill in the blanks

Question 1.
D-glucose and L-glucose form a pair of ……………. .
Answer:
isomers

Question 2.
An aldehyde containing monosaccharide having six carbon atoms is generally called as ………….. .
Answer:
glucose

Question 3.
Inulin is found as a storage polysaccharide in the members of …………. family.
Answer:
compositae

Question 4.
…………… is known as imino acid.
Answer:
Proline

Question 5.
The derived amino acids are also known as …………. amino acids.
Answer:
non-standard

Question 6
…………… is the building block of nucleic acids.
Answer:
Nucleotide

Question 7.
The pentose sugar present in DNA is known as ……………. .
Answer:
deoxyribose

Question 8.
Butyric acid is the only fatty acids with ………….. number of carbons.
Answer:
4

Question 9.
Tocopherols are known as vitamin …………… .
Answer:
E

Question 10.
ß-carotene yields vitamin …………… .
Answer:
A

Suggest one word expression for each the following

Question 1.
The polysaccharide found as reserve food in animal.
Answer:
Glycogen

Question 2.
The compound rotating the plane of polarised light to the right.
Answer:
Dextrorotatory

Question 3.
The polysaccharide found in the exoskeleton of arthropods.
Answer:
Chitin

Question 4.
The branched strach is called as
Answer:
a-D-glucose

Question 5.
The secondary structure exhibited by silk protein.
Answer:
P-Keratin

Question 6.
A protein conformation having two or more subunits.
Answer:
Quaternary structure

Question 7.
Compounds consisting of a N-base, pentose sugar and phosphoric acid.
Answer:
Nucleotide

Question 8.
Compounds obtained by esterification of alcohol group of glycerol with fatty acids.
Answer:
Lipids

Short Answer Type Questions

Write notes on

Question 1.
Disaccharides
Answer:
(a) Disaccharides These are the sugars containing two monomeric units and can be further hydrolysed into smaller components. These are known as non-reducing sugars because the free aldehyde or ketonc group is absent, e.g., sucrose (α-D Glucose + ß- D Fructose), maltose (α-D Glucose + ß-D glucose), lactose (ß-D Galactose + α-D Glucose) etc.

Question 2.
Anomers
Answer:
Anomers These are the distereoisomers of the cyclic forms of sugars differing in the configuration at anomeric carbon 1, e.g. α-form and ß-form of glucose.

Question 3.
Homopolysaccharides
Answer:
These are those complex carbohydrates which are formed by polymerisation of only one type of monosaccharide monomers, e.g., starch, glycogen and cellulose (these all are composed of single type of monosaccharide unit namely glucose).

Question 4.
Mucopolysaccharides
Answer:
Mucopolysaccharides These are the polysaccharides forming slimy substances or mucilages and composed of mixture of simple sugars and their derivatives such as amino sugars and uranic sugars, e.g. hyaluronic acid.

Question 5.
Quaternary structure of proteins
Answer:
Quaternary Structure:
Certain proteins consist of an assembly of more than one polypeptide or subunits. These, the individual polypeptides are arranged with respect to one another (linear strings of spheres, spheres arranged one upon each other in the form of a cube or plate, etc.) e.g. haemoglobin, lactic acid dehydrogenase enzyme.

Question 6.
Non-standard amino acids
Answer:
Non-standard amino acids are the derived amino acids from the 20 standard amino acids.
e.g. hydroxyproline (derived from proline) and hydroxylysine (derived from lysine) are abundant in collagen.

Question 7.
Non-protein amino acids
Answer:
Non-protein amino acids These are natural amino acids which are not found as constituents of proteins but have some role in metabolism, e.g.
L-ornithine and L-citrulline are metabolic intermediates in urea-cycle.
ß-alanine, an isomer of alanine, occur in nature freely and a major constituent of vitamin pantothenic acid and coenzyme-A.

Question 8.
Classification of proteins based on shape
Answer:
On the basis of shape of the molecules proteins can be of two types
(i) Globular Proteins They are extensively folded and compact polypeptides having rounded shape. They are generally soluble in water and in dilute acids, alkalis, salts. They have axial ratio (length : width) of less than 10 (usually 30 H) e.g., almost all enzymes, protein hormones, blood transport proteins, antibodies (serum globulins), nutrient storage proteins, etc.

(ii) Fibrous Proteins The proteins have spiral secondary polypeptide chains wound around each other in order to form fibres. These are insoluble in water generally, but soluble in concentrated acids, alkalis and salts, e.g., collagen of connective tissue, keratin of hair, etc. They have axial ratio greater than 10, mainly of animal origin and slewes as structural or protective proteins.

Question 9.
Polyunsaturated fatty acids
Answer:
Polyunsaturated fatty acids These are several double bonds. In the most common of such acids, a methylene group separates the non-conjugated double bonds. The melting point of fatty acids decrease with increasing number of double bonds.

Question 10.
Chemical nature of enzyme
Answer:
The chemical nature of enzymes remained in dispute untils 1926, when James B Summer became succesful in purifying and crystallising the enzyme urease from jack bean. His results established that the enzyme urease is a protein. Subsequendy, John H. Northrop and Wendell M. Stanley purified and characterised a series of digestive enzymes. They confirmed Summer’s result and proved without doubt that enzymes are proteins. Since then thousands of enzymes have been purified and characterised, and all enzymes are found to be protein.

Question 11.
Activation energy
Answer:
The conversion of reactants to products in any chemical reaction is accompanied by continuous change in energy. These changes can be pictorially represented through a graph as given below. In the graph T-axis represents the potential energy content and the X-axis represents the progression of the structural transformation (states through the transition state).

Question 12.
Enzyme substrate complex.
Answer:
Each enzyme (E) has a substrate (S) binding site in its molecule in order to form a highly reactive Enzyme Substrate (ES) complex. This complex is short lived and dissociates into its product (P) and unchanged enzyme with an intermediate formation of the Enzyme Product (EP) complex.

Long Answer Type Questions

Question 1.
Describe the structure of DNA.
Answer:
Structure of DNA
The structure of DNA was elucidated by Watson and Crick based on X-ray diffraction studies. They proposed a double helix model of DNA.
According to this model, DNA exists as a double helix and consists of two strands of polynucleotides that are antiparallel to each other, i.e. both run in opposite directions, one in 5′ → 3′ direction and other in 3′ → 5′ « direction.

Diagram indicating secondary structure of DNA

The backbone of DNA is formed by the sugar phosphate-sugar chain. The nitrogen bases are projected more or less perpendicular to the backbone of DNA and faces inside. A and G of one strand base pairs with T and C, respectively on the other strand. Between A and T (A= T), there are two hydrogen bonds while, there are three hydrogen bonds between G and C (G=C).

DNA has a uniform thickness of 20 A and pitch is 34 nm. Thus, one turn of DNA measures 3.4 nm (rise per base pair) and consists of 10 nucleotides (or ten base pairs). This form of DNA is called B-DNA.

Question 2.
Describe the structures of different types of RNA.
Answer:
Ribonucleic Acid (RNA):
RNA is a polynucleotide made of ribonucleotide units having ribose sugar, phosphoric acid and one of the nitrogen bases. DNA serves as the template for the synthesis of RNA. Cellular RNAs are non-genetic and are of three types namely mRNA, /RNA and rRNA.

(i) Messenger RNA (mRNA):
It is the RNA formed during the protein synthesis. Five to ten percent of cellular RNA is of this type. The molecular weight of wRNA varies from 30000-1000000. It is short lived. DNA transfers the genetic information to ribosome through this type of RNA during the protein synthesis.

(ii) Ribosomal RNA (rRNA)
The most stable form of RNA in the cell is the rRNA. About 80% of cellular RNA is of this type. The molecular weight or rRNA ranges from 40000-1000000. It may have some folds to have a complex structure. rRNA units along with protein constitute the protein synthesising factory or the ribosome.

(iii) Transfer RNA (tRNA)
It is the smallest form of RNA made of only 75 to 100 nucleotides. It is also known as the soluble RNA. It forms about 10-15% of total cellular RNA. The molecular weight of tRNA varies from 25000-30000. It transfers the amino acids from the cytoplasm to the ribosome.

In 1964 Holley gave the detailed structure of tRNA through the ‘Clover leaf model’. In that model it was proposed that tRNA has three loops and a lump. The anticodon loop has the complementary base sequence with respect to a codon of mRNA facilitating the attachment of tRNA with the later. Other two loops are TψC loop or ribosomal binding loop and DHU loop or amino acyl synthetase binding loop. The 3’ end of rRNA ends with CCA-OH, which acts as the amino acid attachment site. The other end with G.

Question 3.
Describe the properties of enzymes indicating how they differ from chemical catalysts.
Answer:
The term ‘Enzyme’ was coined by Kuhne. Enzymes are colloidal organic macromolecules, which are mostly proteinaceous in nature except ribozyme (catalytically active RNA). These are essential for normal metabolism in the cells. Enzymes are water soluble in nature. These are useful for catalysing biochemical reactions in living cells. Hence, also known as biocatalysts.

Chemical Nature of Enzymes
The chemical nature of enzymes remained in dispute untils 1926, when James B Summer became succesful in purifying and crystallising the enzyme urease from jack bean. His results established that the enzyme urease is a protein. Subsequendy, John H. Northrop and Wendell M. Stanley purified and characterised a series of digestive enzymes.

They confirmed Summer’s result and proved without doubt that enzymes are proteins. Since then thousands of enzymes have been purified and characterised, and all enzymes are found to be protein.

As it is already studied that simple enzyme are composed of one or several polypeptide chains.
Certain enzymes possess non-protein constituents called cofactors bound to the protein part of the enzyme in order to make it catalytically active. An enzyme plus cofactor complex is called holoenzyme. An enzyme that has had its cofactor removed is called apoenzyme.

Categories of cofactor

Question 4.
Write the mechanism of enzyme actions.
Answer:
Mechanism of Enzyme Action:
The mechanism of enzyme action includes two parameters i.e. formation of enzyme, substrate complex and activation energy.
Formation of Enzyme Substrate Complex
For a chemical reaction to proceed, the substrate (S) must bind to enzyme at the active site within a cleft or pocket. During conversion of substrate into a product, formation of an enzyme-substrate complex takes place.
E (enzyme) + S (substrate) → ES complex.

This complex formation is a transient phenomenon. Thus, during the state, when substrate is bound to the enzyme active site, a new structure of the substrate, called transition state structure is formed.

After the expected reaction of breaking and making of bond is completed, the product is released from the active site and the substrate gets transformed into the structure of product.

Activation Energy:
The conversion of reactants to products in any chemical reaction is accompanied by continuous change in energy. These changes can be pictorially represented through a graph as given below. In the graph T-axis represents the potential energy content and the X-axis represents the progression of the structural transformation (states through the transition state).

Following levels are noticed between the energy levels of S and P
(i) When P is at a lower level than S, reaction is . exothermic or spontaneous, i.e. no need for external supply of energy.
(ii) When P is at higher level than S, reaction is endothermic or energy requiring reaction, i. e. external supply of energy is needed.

Concept of activation energy

It proves that whether it is an exothermic or an endothermic state, the ‘S ’ has to go through a much higher energy state (transition state). This difference between the average energy content of S from that of its transition state is called activation energy.

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 8 Cell: Structure and Function Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 8 Question Answer Cell: Structure and Function

Cell: Structure and Function Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Multiple choice questions

Question 1.
Which one of the following organelles is without membrane envelop?
(a) Golgi complex
(b) ribosome
(c) peroxisome
(d) tonoplast
Answer:
(b) ribosome

Question 2.
The figures of cork cells as seen by Robert Hooke were published in his book.
(a) origin of species
(b) plant kingdom
(c) genera plantarum
(d) micrographia
Answer:
(d) micrographia

Question 3.
Prokaryotic cell is that which has
(a) primitive nucleus
(b) true nucleus
(c) two nuclei
(d) four nuclei
Answer:
(a) primitive nucleus

Question 4.
Which of the following cells does not contain a nucleus?
(a) yeast
(b) nerve cells
(c) mature WBC
(d) mature RBC
Answer:
(d) mature RBC

Question 5.
Protein and RNA are the principal constituents of
(a) ribosome
(b) chromosome
(c) endoplasmic reticulum
(d) peroxisome
Answer:
(a) ribosome

Question 6.
70s ribosomes are found in
(a) mitochondria and bacteria
(b) mycoplasma and eukaryotic cell
(c) RBC and WBC
(d) epidermal cells and hepatic cells
Answer:
(a) mitochondria and bacteria

Question 7.
Which of the following cell organelles is bound by a single unit membrane?
(a) Golgi apparatus
(b) chloroplast
(c) mitochondrion
(d) lysosome
Answer:
(d) lysosome

Question 8.
Which of the following is the site of steroid synthesis
(a) rough endoplasmic reticulum
(b) ribosomes
(c) smooth endoplasmic reticulum
(d) mitochondrion
Answer:
(c) smooth endoplasmic reticulum

Question 9.
The physical basis of life is
(a) nucleus
(b) protoplasm
(c) cell
(d) food
Answer:
(b) protoplasm

Question 10.
Every living cell possesses
(a) chloroplast
(b) cell membrane
(c) cell wall
(d) food vacuole
Answer:
(b) cell membrane

Question 11.
The chemical substance most abundantly present in the middle lamella is
(a) lignin
(b) suberin
(c) chittn
(d) pectin
Answer:
(d) pectin

Question 12.
The latest model proposed to explain the structure of plasma membrane is
(a) molecular model
(b) sandwich model
(c) unit membrane model
(d) fluid-mosaic model
Answer:
(d) fluid-mosaic model

Question 13.
The peripheral proteins can be easily removed from the membrane by
(a) the action of detergent
(b) solutions of high ionic strength
(c) keeping them in buffer
(d) enzyme action
Answer:
(b) solutions of high ionic strength

Question 14.
Tonoplast is a differentially permeable membrane sorrounding
(a) cytoplasm
(b) mitochondrion
(c) vacuole
(d) nucleus
Answer:
(c) vacuole

Question 15.
F₁ -particles are present in
(a) chloroplast
(b) mitochondrion
(c) dictyosome
(d) nucleus
Answer:
(b) mitochondrion

Question 16.
Double membrane is absent in
(a) nucleus
(b) chloroplast
(c) mitochondrion
(d) lysosome
Answer:
(d) lysosome

Question 17.
Polyribosomes are aggregation of
(a) ribosomes on r RNA
(b) Only r RNA
(c) peroxisomes
(d) ribosomes on m RNA
Answer:
(d) ribosomes on m RNA

Question 18.
Ribosomes are attached to ER through
(a) ribophorins
(b) r RNA
(c) t RNA
(d) hydrostatic force
Answer:
(a) ribophorins

Question 19.
The cytoplasmic ribonucleoprotein that binds to free ribosomes so that protein synthesis stops till ribosomes get associated with ER is known as
(a) SPR
(b) SRP
(c) PRS
(d) PSR
Answer:
(b) SRP

Question 20.
Lysosomes are called “suicidal bag” because they have
(a) hydrolytic enzymes
(b) parasitic activity
(c) anabolic enzymes
(d) oxidizing enzymes
Answer:
(a) hydrolytic enzymes

Question 21.
In plant cells the vacuole contains
(a) gases
(b) vacuum
(c) dissolved minerals
(d) only water
Answer:
(c) dissolved minerals

Question 22.
ATP, the energy currency of cell, is synthesised mostly in
(a) ribosomes
(b) mitochondria
(c) lysosomes
(d) nucleus
Answer:
(b) mitochondria

Question 23.
Ribosomes are made up of
(a) RNA and DNA
(b) DNA and proteins
(c) RNA and proteins
(d) RNA alone
Answer:
(c) RNA and proteins

Question 24.
When green tomatoes turn red
(a) chromoplasts change to chloroplasts
(b) chloroplasts change to chromoplasts
(c) new chromoplasts are synthesised
(d) new chloroplasts are synthesised
Answer:
(b) chloroplasts change to chromoplasts

Question 25.
Thylakoids are seen in the plastids of
(a) higher plants
(b) bacteria
(c) algae
(d) blue-green algae
Answer:
(a) higher plants

Question 26.
Foldings of inner mitochondrial membrane are called
(a) cristae
(b) grana
(c) sacs
(d) dictyosomes
Answer:
(a) cristae

Question 27.
Ribosomes of prokaryotes are of
(a) 30s type
(b) 50s type
(c) 70s type
(d) 80s type
Answer:
(c) 70s type

Question 28.
If the ribosomes of a cell are destroyed or blocked, then
(a) respiration will stop
(b) digestion will stop
(c) reproduction will stop
(d) protein synthesis will stop
Answer:
(d) protein synthesis will stop

Question 29.
Site of formation of immature ribosomal sub-units in eukaryotic cell is
(a) cytoplasm
(b) nucleus
(c) nucleolus
(d) nuclear pore complex
Answer:
(c) nucleolus

Question 30.
The main function of Golgi complex is
(a) translocation
(b) fermentation
(c) protein glycosylation
(d) phosphorylation
Answer:
(a) translocation

Question 31.
Peroxisomes contain
(a) transferase enzymes
(b) hydrolytic enzymes
(c) isomerase enzymes
(d) oxidizing enzymes
Answer:
(d) oxidizing enzymes

Question 32.
Nucleoli are rich in
(a) DNA and RNA
(b) DNA, RNA and proteins
(c) DNA
(d) RNA
Answer:
(b) DNA, RNA and proteins

Question 33.
Nucleus was first discovered by
(a) Leewenhoek
(b) Schwann
(c) Robert Brown
(d) Robert Koch
Answer:
(c) Robert Brown

Question 34.
Microtubules are made up of
(a) myosin
(b) actin
(c) tubulin
(d) globulin
Answer:
(c) tubulin

Question 35.
Centromere is a part of
(a) ribosome
(b) chromosome
(c) spherosome
(d) glyoxisome
Answer:
(b) chromosome

Question 36.
Chromosomes with equal arms are called
(a) submetacentric
(b) polycentric
(c) acentric
(d) metacentric
Answer:
(d) metacentric

Question 37.
The hydrophobic chemicals like pesticides and carcinogens are detoxified by enzymes found in
(a) mitochondrion
(b) lysosome
(c) Golgi
(d) SER
Answer:
(b) lysosome

Question 38.
Which of the followings is a prokaryote?
(a) Agaricus
(b) Salmonella
(c) Volvox
(d) Saccharomyces
Answer:
(b) Salmonella

Fill in the blanks

Question 1.
…………. is the cytoplasmic organelle, responsible for cellular respiration.
Answer:
Mitochondria

Question 2.
…………. proposed the unit membrane concept.
Answer:
J. David Robertson

Question 3
…………. is the largest cytoplasmic organelle in plant cell.
Answer:
Plastid

Question 4.
…………. is the smallest cytoplasmic organelle.
Answer:
Ribosome

Question 5.
…………. is a vesicle containing digestive enzymes found in a cell.
Answer:
Lysosome

Question 6.
Intracellular digestion is associated with …………. .
Answer:
Lysosomes

Question 7
…………. maintains the cytoplasmic continuity between neighboring cells.
Answer:
Plasmodesmata

Question 8.
Singer and Nicholson proposed the …………. model for plasma membrane.
Answer:
Fluid-mosaic

Question 9.
Presence of DNA in chloroplasf and mitochondria make them …………. .
Answer:
Semi-autonomous

Question 10.
Colored plastids found in flowering plants are known as …………. .
Answer:
Chromoplast

Question 11.
A chromosome lacking a centromere is …………. .
Answer:
Acentric

Question 12.
Prokaryotic cells contain …………. ribosomes.
Answer:
70S

Question 13.
Histone proteins are …………. by nature.
Answer:
Basic

Question 14.
The portion of DNA between two repeating units of nucleosomes is known as …………. DNA.
Answer:
Linker

Question 15.
When two solutes move across the cell membrane in opposite directions the transport is known as …………. .
Answer:
Antiport

Short Answer Types Questions

Write notes on

Question 1.
Cell wall
Answer:
Cell wall: It is a rigid or semi-rigid envelope lying outside the cell membrane of plants, fungi, etc. It helps in maintaining shape and protecting them from osmotic lysis. It possess three structural components namely middle lamella, primary wall and secondary wall.

Question 2.
Mitochondrion
Answer:
Mitochondrion : These are membrane bound cell organelles, essential for aerobic respiration of eukaryotic cells. These are also known as powerhouse of the cell because, they produces cellular energy in the form of ATP.

Question 3.
Plastids
Answer:
Plastids : These are semi-autonomous organelles that have double membrane envelope. Plastids have their own genetic material (i.e., DNA). Due to their large size, they are easily seen under the microscope. The term plastid was coined by E Haeckel in 1866.

Question 4.
Ribosome
Answer:
Ribosomes : These are small subspherical granular organelles, not bounded by any membrane. Ribosomes were first observed by George Palade (1953), as the dense particles under the electron microscope. Hence, are also called Palade particles.
Ribosomes are mainly composed of ribonucleoproteins (i.e., RNA + proteins) and are also known as protein factories, as they are primarily involved in the synthesis of proteins or polypeptides.

Question 5.
ER
Answer:
Endoplasmic Reticulum : It is a complicated system of membranous channels and flattened vesicles. It is physically continuous with the outer membrane of the nuclear envelope. It is revealed from the electron microscopic studies of eukaryotic cells that there is a presence of a network or reticulum of tiny tubular structures that are being scattered in the cytoplasm.
Note ER is known to be absent in prokaryotes, but is present in all eukaryotic cells except germinal cells and mature human RBCs.

Question 6.
Golgi complex
Answer:
Golgi complex : Golgi complex or Golgi apparatus is a complex protoplasmic structure made up of many flat, disc-shaped sacs or cisternae (0.5-1.0 pm) in diameter), surrounded by vesicles.
Cisternae of Golgi apparatus are found to be stacked parallel to each other. They vary in number in a cell.
They are often curved like shallow bowls to give Golgi complex a definite polarity.

Question 7.
Lysosome
Answer:
Lysosome : These are membrane bound polymorphic vesicles that are produced by the Golgi apparatus. They are rich in several hydrolytic digestive enzymes (hydrolases-lipases, proteases, carbohydrases, etc). These enzymes are usually active at the acidic pH (less than 7). Therefore, are also called acid hydrolases and are capable of digesting macromolecules from various sources like carbohydrates, lipids and nucleic acids.

Question 8.
Vacuole
Answer:
Vacuole : These are large membranous sac found in the cytoplasm. These store substances that are not essentially useful for the cell (like water, sap, excretory product and other materials). Plant vacuoles contain not only water, sugars and salts, but also contain pigments and toxic molecules and also occupy upto 90% of the volume of the cell.

Question 9.
Flagella
Answer:
Flagella : They are long, whip-like organelle. They are fewer im membrane per cell and found at either end of a cell. They show undulatory motion. They are found in prokaryotic bacteria.

Question 10.
Nuclear pore
Answer:
Nuclear pore : Nuclear pores are the openings/pores in the nuclear envelope, formed by the fusion of its two membranes. These pores help in the exchange of materials, especially RNA, proteins, ribosomes, etc., between the cytoplasm and nucleoplasm.

Question 11.
Microtubules
Answer:
Microtubules : They were first observed in nerve cells by De Roberties and Franchi in 1953. They are thin, branched, hollow cylinder of about 20-25 nm diameter.
Each microtubule is composed of 11-13 longitudinal strands of protein protofilaments which encloses a central core. The protofilaments are formed by the polymerisation of a and 1 tubulin powered by the hydrolysis of GTP.

Question 12.
Nucleosome
Answer:
Nucleosome : The DNA in eukaryotic chromosome are very large molecules. Thus, they requires proper packaging of DNA inside the chromoesome in such a way that DNA is compact and functional.

Question 13.
Unit membrane concept
Answer:

• Proposed by j David Robertson in 1959.
• According to it, all biological membranes have the basic unit membrane structure of three layers two outer electron dense layer and one middle electron transparent layer.
• Each dense layer is constituted by protein of 15A thickness and the transparent layer is of bilayer of lipid of 45A thickness.

Long Answer Type Questions

Question 1.
What are chromosomes? Describe their structure and functions.

It has been already studied in the chapter that the nucleus in the interphase has a loose and indistinct network of nucleoprotein fibres called chromatin. However, during different stages of cell division cells show structured chromosomes in place of the nucleus. The chromosomes are meant for the equal distribution of genetic piaterial. Their number is fixed and is same in all individuals of a species. A single human cell has approximately two metre long thread of DNA distributed among its 46 (23 pairs) chromosomes.
Each and every chromosome is composed of a primary constriction or the centromere. On the sides of which the disc-shaped structures known as kinetochores are present

Structure of a typical somatic chromosome during anaphase

Gross Morphology:
On the basis of the position of the centromere, the chromosomes can be classified into following four types

• Metacentric It has chromosome with equal arms and centromere lies in the centre.
• Submetacentric It has one shorter arm and one longer arm with centromere slightly away from the middle of the chromosome.
• Acrocentric It forms one extremely short and one very long arm and centromere is located near the end of the chromosome.
• Telocentric It has the terminal centromere, i.e., placed at an extreme end. Telocentric chromosomes are not present in humans.
  
  Types of chromosomes based on the position of centromere

Few chromosomes have a non-staining secondary constrictions being present at a constant location at some or the other time which gives the appearance of a small fragment known a satellite.

Chemical Composition:
Chromatin is composed of DNA and some basic proteins called histones. Some non-histone proteins and RNA are also present in the chromatin.

Functions:
Chromosomes performs the following functions

• Control cellular differentiation.
• Contains all hereditary information located in the genes.
• Forms a link between the offspring and the parents.
• Introduce variations, through the process of crossing over.
• Control cell metabolism.

Nucleosome Concept:
The DNA in eukaryotic chromosome are very large molecules. Thus, they requires proper packaging of DNA inside the chromoesome in such a way that DNA is compact and functional.

This is achieved by compacting DNA with the help of histone protein into repeating units called nucleosomes (Roger Kornberg, 1974).
Accroding to this concept five type of histones are found in enkaryotes namely H₁, H₂A, H₂R , H₃ and H₄.
Two molecules each of H₂A, H₂B, H₃ and H₄ together form an octamer called core of nucleosome or Nu-bodies.

A DNA fragment of about 146 base pair wrap around the core 1.75 times and one molecule of H1 associate with it. According to A Klug (Nobble Prize Winner, 1982) this chain of nucleosome is coiled into cylindrical solenoid fibrils of 10 nm having about six nucleosomes per turn. This is further coiled into super solenoid of 30nm (interphase chromatin). During metaphase, it further condense to chromosome.

Question 2.
Explain the fluid-mosaic model of plasma membrane with suitable diagrams.
Answer:
Fluid Mosaic Model
This model was given by Singer and Nicholson (1972). According to this model in a membrane, the lipid bilayer and integral proteins appear like a mosaic arrangement and the quasi-fluid nature of lipid enables the lateral movement of the proteins within the overall bilayer.

This molecular arrangement is stable because it maximisze the contact of hydrophilic regions of proteins and phospholipids with water while providing the hydrophobic parts with a non-aqueous environment.
Freeze fracture technique has provided the most compelling evidence that proteins are embedded in lipids.

Fluidity of Membrane:
The fluid nature of the membrane is important from the point of view of interactions of molecules within the membrane as well as other functions like formation of intercellular junctions, cell growth, secretion, endocytosis, cell division, etc.
Cell membrane also controls the movement of various substances.

Functions:
Cell membrane performs the following functions
It is a selectively permeable or semipermeable membrane that allows only selected substances to pass through.
It protects the cell from injury.
Membranes have carrier proteins for active transport.
Cell membrane contains enzymes which perform certain reaction on their surface, e.g., ATPase, phosphatase, etc.

Question 3.
What are organelles? Give an account of principal organelles of a cell and mention their functions.
Answer:
A cell which has a well-organised nucleus with a nuclear envelope and several membrane bound organelles is called eukaryotic cell. Internal organisation of eukaryotic cells is more advanced and elaborate, than the prokaryotic cells. Except monerans, eukaryotic organisation is seen in all the protists, plants, fungi and animals. Eukaryotic cell is larger than the prokaryotic cell (i.e., around 10-100 p,m in size).

In eukaryoticcells, an extensive compartmentalisation of cytoplasm is seen through the presence of membrane bound organelles. Eukaryotic cells also possess a variety of locomotory and cytoskeletal structures. All eukaryotic cells are not identical, instead they differ from each other on the basis of structure and function.

Plant Cell and Animal Cell:
Ceil wall is a special membrane, being present in plants, fungi and some protists. Plants cells also contain a large vacuole and plastids, which are absent in animal cells, while animal cells possess centrioles, which are absent in plant cells.
Differences between plant and animal cell

Components of a Eukaryotic Cell:
A eukaryotic cell is composed of various cell components as cell membrane, cell wall (only in plants), mitochondria, chloroplast, Golgi bodies, ribosomes, centrioles (only in animals), etc. All these are described here under in detail.

Cell Wall
It was first discovered by Robert Hooke (1665). It is a rigid and non-living structure which forms an outer covering of the plasma membrane in plants and fungi. It is absent in animal cells.

Components of Cell Wall
(i) Plant cell walls are made up of cellulose which is an unbranched polysaccharide of D-Glucose units linked together by [5-1, 4-glycosidic bond.
(ii) Cell walls of fungi possess chitin while algae have glycoprotein and polysaccharides. A few algae also contain silicic acid and other accessory molecules in cell wall.

Enzymatic and Structural Proteins in Cell Wall
(i) Cell wall contains numerous hydrolases like invertase, glucanases, pectin methyl esterases and phosphatases. Several oxidases are also present in cell wall including ascorbic acid oxidase and laccase involved in lignin formation.
(ii) The most abundant structural proteins are Hydroxyl proline Rich Glycoprotein (HRGP) also called extensin, Arabinogalactan Protein (AGP), Glycine Rich Proteins (GRPS) and Proline Rich Protein (PRP). Except GRPS, the rest are glycoproteins and contain hydroxyl proline.
Extensin connects pectin and hemicelluloses.

Structure of Cell Wall
On the basis of the structure, cell wall is differentiated into three parts namely middle lamella, primary wall and secondary wall.

(a) Middle Lamella It is a thin amorphous layer that cement the cell walls of two adjoining cells together. It is the first formed layer and formed during cytokinesis. It is mainly made up of calcium and magnesium pectate.
It is absent on the outer side of cell surface. The pectic substances of this layer are enzymatically converted to partially soluble substances during fruit ripening.

(b) Primary Cell Wall It is produced inner to the middle lamella in a young and growing cell.
It is composed of cellulose, hemicellulose and pectin. The cellulose microfibrils are linked via hemicellulose teethers to form the cellulose-hemicellulose network which is embedded in pectin matrix. Most commonly » occuring hemicelluloses are xylans or xyloglycans.
Mannans and galactans are also found in it. Pectin, the polymer of a-D-galacturonic acid fills the spaces of matrix. The cellulose microfibrils are aligned at all angles and are held together by hydrogen bonds to provide high tensile strength.

(c) Secondary Cell Wall The thick secondary wall is formed inner to the primary wall towards the cell membrane.
Unlike primary cell wall, the cellulose microfibrils are aligned mostly in same direction and with each additional layer the direction of alignment changes slightly. It is strengthened by the deposit of lignin which are polymers of phenyl propane residues.
This wall is laid down by a process called accretion or deposit of material over the surface of existing structure. It is found in trachieds, vessels, fibres and collenchyma, etc. In certain gymnosperms, this layer consist of xylans. This layer is then called tertiary wall.

Functions:
Cell wall performs the following functions
It helps in providing a definite shape to the cell and also protects protoplasm against any mechanical injury, i.e., damage and infection.

• It helps in cell-to-cell interaction.
• It provides barrier to undesirable macromolecules and attack of pathogens.

Cell Wall Growth
The growth of the cell wall takes place in two ways
(i) Intussusceptions It is the growth from within. Area of the cell wall increases in this way. The primary wall is stretched and material of secondary wall are deposited.
(ii) Apposition It is the growth from outside. The thickness of the cell wall increases in this way. Materials of secondary walls are deposited in thin layers.

Functions:
Golgi apparatus performs the following functions
(i) The Golgi apparatus is involved in the formation of lysosomes, vesicles that contain proteins and remains within the cell.
(ii) It performs the function of packaging of material.
(iii) It acts as an important site for the formation of glycoproteins and glycolipids.
(iv) It helps in the production of complex carbohydrates other than glycogen and starch.
(v) It helps in the formation of cell wall.

Lysosomes:
These are membrane bound polymorphic vesicles that are produced by the Golgi apparatus. They are rich in several hydrolytic digestive enzymes (hydrolases-lipases, proteases, carbohydrases, etc). These enzymes are usually active at the acidic pH (less than 7). Therefore, are also called acid hydrolases and are capable of digesting macromolecules from various sources like carbohydrates, lipids and nucleic acids. Two general classes of lysosomes are usually distinguished. These are as follows
(i) Primary Lysosomes Newly formed lysosomes that has not yet encountered the substrate for digestion.
(ii) Secondary Lysosomes (heterophagosomes)

Membranous sacs of diverse morphology and contains substrates and hydrolytic enzymes. They result from repeated fusion of primary lysosomes with membrane bound substrate. They form large digestive vacuoles, multivesicular bodies, autophagosomes, etc.

Functions:
Lysosomes performs the following functions
(i) They digest the food contents (intracellular digestion).
(ii) They also perform extracellular digestion.
(iii) They also digest the old and useless organelles of the cells.
(iv) They also have functioning in cell division.
(v) Principle site of cholesterol assimilation from endocytosed serum lipoprotein.
(vi) Programmed cell death during embryogenesis.

Vacuoles:
These are large membranous sac found in the cytoplasm. These store substances that are not essentially useful for the cell (like water, sap, excretory product and other materials). Plant vacuoles contain not only water, sugars and salts, but also contain pigments and toxic molecules and also occupy upto 90% of the volume of the cell.

The vacuole is bounded by a single membrane structure known as tonoplast which in plant cells, facilitates the transport of materials and some ions against the concentration gradient inside the vacuole. Thus, the concentration of materials tends to be higher in vacuole, than to be in the cytoplasm. Animal cells also have vacuoles, but they are much more prominent in case of plant cells. Thus, plant cells have typically large central vacuoles filled with a watery fluid that gives added support to the cell.

Functions
(i) Storage of reserve food like sucrose, minerals, etc., and secondary metabolites like tannin, latex, etc.
(ii) Impart turgidity to the cell as they contain high solute concentration.

Question 4.
What are the different types of plastids seen in plants? Describe the structure and function of chloroplast
Answer:
Plastids:
These are semi-autonomous organelles that have double membrane envelope. Plastids have their own genetic material (i.e., DNA). Due to their large size, they are easily seen under the microscope. The term plastid was coined by E Haeckel in 1866.

Occurrence
Plastids are found in all plant cells and euglenoides except in some protistans (e.g. Euglena, Dinophyceae, etc).

Types
All plastids are derived from proplastids called eoplasts. Plastids are differentiated into three different types on the basis of the colour, i.e., type of pigments found in them.
(i) Chloroplasts These are the plastids which are greenish in colour containing photosynthetic pigments chlorophyll and carotenoids.
(ii) Chromoplasts These are plastids, which are yellow or reddish in appearance because of the presence of fat soluble carotenoid pigment carotene. Xanthophyll and some other pigments are also present as the fat soluble carotenoid pigment other than carotene, e.g. orange colour of carrot is due to the presence of chromoplasts.
(iii) Leucoplasts These are the colourless plastids of varied shapes and sizes with stored nutrients in the form of carbohydrates, lipids and proteins. These are of following three types
(a) Amyloplasts are the carbohydrates (starch) containing leucoplast, e.g. rice, wheat, potato, etc. Amyloplasts are larger than the normal/original size of leucoplast.
(b) Elaioplasts are the leucoplast which store oils and fats, e.g. tuberose endosperm of castor seeds, etc.
(c) Aleuroplasts (Proteinplast) are the protein storing leucoplasts. e.g. maize (aleurone cells).

Chloroplast:
Schimper (1883) coined the term chloroplast. These are double membrane bound cell organelles that play a major role in photosynthesis.

Occurrence
Chloroplasts occur in major number in the photosynthetic mesophyll cells of leaves and green stem.

Shape and Size
They may be lens-shaped, oval, spherical, discoid or even ribbon-like. They are cup-shaped in Chlorella and Chlamydomonas, girdle-shaped in Ulothrix and spiral in Spirogyra.
They also have variable length (5-10 mm) and width (2-4 mm).

Number:
Their number also varies from 1 per cell in Chlamydomonas (a green alga) to 2-40 per cell in mesophyll cell.

Ultrastructure
Chloroplasts are consists of the two membranes that are smooth and thick (about 90-100 A). The inner membrane of chloroplast is less permeable than the outer one.

The inner membrane is grounded by a space known as stroma or matrix, a dense, colourless and a granular substance mainly formed of soluble proteins. It also contains enzymes which are essential for the synthesis of carbohydrates, lipids and proteins.

In the stromata, thylakoids are present. These are membranous flattened structures that run throughout the matrix or stroma. Several thylakoids are arranged or organised in stack (like the piles of coins), called grana or the intergranal thylakoids. Many flat membranous tubules that interconnect the thylakoids of different grana are known as stromal lamellae.

Functions:
Chloroplasts perform the following functions
(i) Help in photosynthesis, i.e. formation of organic compounds.
(ii) In consumption of CO₂ and release of O₂ in photosynthesis.
(iii) May also change into chromoplast in order to provide colour to many flowers and fruits.
(iv) Help in storing fat and lipids.
(v) Function in transduction of energy.

Knowledge Plus
• The algal chloroplast are agranal as they lack grana.
• The chloroplast with nitrogen-fixing genes are called nitroplast.
• The space between the two membrane is called intermembrane space, which separates the two membrane. This space contains a narrow fluid. Stroma also contains small, double-stranded circular DNA, molecules and ribosomes.
• Ribosomes of chloroplasts are smaller (70S) than the ribosomes of cytoplasm (80S).

Differentiate between

Question 1.
Cell wall and plasma membrane
Answer:
Differences between cell wall and plasma membrane are

Cell wall	Plasma membrane
Rigid, protective, supportive layer.	Dynamic, quasifluid, film-like layer.
Thickness is about 0.1 pm to 10 pm.	Thickness is about 7.5 nm.
Consist of cellulose or peptioglycan/chitin, etc.	Consists of lipids proteins, carbohydrates, etc.
It is not selectively permeable.	It is selectively permeable.

Question 2.
Chloroplast and mitochondrion
Answer:
Differences between chloroplast and mitochondrion are

Question 3.
Cytoplasm and karyolymph
Answer:
Differences between cytoplasm karyolymph are

Question 4.
Leucoplast and chloroplast
Answer:
Differences between leucoplast and chloroplast

Leucoplast	Chloroplast
Colourless plastids	Green-coloured plastids.
Mainly found in the roots of plants.	Found in leaves of plants.
Acts as storehouse of minerals and nutrients.	Take part in photosynthesis.
They lack grana and photosynthetic pigments.	Possess grana and photosynthetic pigment

Question 5.
Chromatin and chromosome
Answer:
Differences between chromatin and chromosome

Chromatin	Chromosome
It is uncondensed part of nucleoprotein complex.	Chromosomes are condensed parts of the nucleoprotein complex.
Chromatin is observable in the interphase nucleus.	Chromosomes are observable during M-phase or nuclear division.
Chromatin is in the form of fine fibrils that run throughout the nucleus.	Chromosomes are in the form of short thick threads or rods.
Replication occurs in the chromatin phase.	It cannot occur in chromosome phase.
The replicas are not visible.	Replicas are visible as chromatids.
It is active in controlling metabolism and other activities of the cell.	Chromosomes are mainly meant for distribution of genetic information to the daughter cells.

Question 6.
Nucleus and nucleolus
Answer:
Differences between nucleus and nucleolus

Nucleus	Nucleolus
Large, spherical structure present in the cell.	Small structure, present inside the nucleus.
Bounded by nuclear envelope.	It has no limiting membrane.
Rich in DNA.	Rich in RNA.
Possess chromosomes and cellular membranes.	Possess fibrillar centres, granular component, etc.

Question 7.
SER and RER
Answer:
Differences between SER and RER
Tablee 8

Question 8.
Intrinsic proteins and peripheral proteins
Answer:
Differences between Intrinsic proteins and peripheral proteins

Intrinsic Proteins	Peripheral Proteins
Embedded in the plasma membrane either partially or completely.	Occur on the surface of plasma membrane.
Constitute 70% of total membrane proteins.	Constitute about 30% of total membrane proteins.
More hydrophobic.	More hydrophilic.
Function as carrier protein, enzymes, transport channels, permeases.	Function as receptors, antigens, recognition centres, etc.
e.g., Glycophorins, rhodopsin, etc.	e.g., erythrocyte spectrin, mitochondrial cyt.c, etc.

Question 9.
Primary cell wall and secondary cell wall
Answer:
Differences between primary cell wall and secondary cell wall

Primary Cell Wall	Secondary Cell Wall
Occur in all plant cells.	Occur in only mature and non-dividing cells.
Present inner to middle lamella.	Present inner to primary cell wall.
Elastic and thin	Inelastic, rigid and thick.
Intussusceptional growth.	Accretional growth.
Pits are absent.	Pits are present.
Contain less amount of cellulose.	Contain high amount pf ‘ cellulose.

 

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 7 Animal Tissues and Gross Anatomical Organisation of Cockroach Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 7 Question Answer Animal Tissues and Gross Anatomical Organisation of Cockroach

Animal Tissues and Gross Anatomical Organisation of Cockroach Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Choose the correct answer

Question 1.
Ligaments and tendons are formed of
(a) muscular, tissue
(b) epithelial tissue
(c) connective tissue
(d) nervous tissue
Answer:
(c) connective tissue

Question 2.
Segment of the skeletal muscle fiber between two Z-lines is called
(a) A-band
(b) H-band
(c) sarcomere
(d) sarcoplasm
Answer:
(c) sarcomere

Question 3.
Schwann cells and nodes of Ranvier are present in
(a) bone cells
(b) neurons
(c) muscle cells
(d) chondrocytes
Answer:
(b) neurons

Question 4.
Notochord originates from
(a) ectoderm
(b) mesoderm
(c) endoderm
(d) None of these
Answer:
(a) ectoderm

Question 5.
Which muscle of body works non-stop till death?
(a) Unstriped
(b) Skeletal
(c) Cardiac
(d) Smooth
Answer:
(c) Cardiac

Question 6.
In an animal, the tissue is bathed in
(a) calcium chloride
(b) body fluid
(c) water
(d) sodium chloride
Answer:
(b) body fluid

Question 7.
Voluntary muscle is present in
(a) lung
(b) liver
(c) heart
(d) hindlimb
Answer:
(d) hindlimb

Question 8.
Non-cellular basement membrane is a feature of
(a) epithelial tissue
(b) vascular tissue
(c) nervous tissue
(d) connective tissue
Answer:
(a) epithelial tissue

Question 9.
A tissue is a group of cells having
(a) similar cells with dissimilar function
(b) similar cells with similar function
(c) dissimilar cells with dissimilar function
(d) dissimilar cells with similar function
Answer:
(b) similar cells with similar function

Question 10.
Intercellular matrix is minimum in
(a) bone
(b) vascular tissue
(c) muscular tissue
(d) cartilage
Answer:
(a) bone

Question 11.
Blood vessels are lined internally by
(a) ciliated epithelium
(b) squamous epithelium
(b) columnar epithelium
(d) striated epithelium
Answer:
(b) squamous epithelium

Question 12.
Transitional epithelium is found in
(a) kidney
(b) urinary bladder
(c) trachea
(d) blood vessel
Answer:
(b) urinary bladder

Question 13.
Tendon connects
(a) muscle to muscle
(b) bone to bone
(c) bone to muscle
(d) nerve to muscle
Answer:
(c) bone to muscle

Question 14.
Cardiac muscle is
(a) voluntary and striated
(b) involuntary and striated
(c) involuntary and smooth
(d) voluntary and smooth
Answer:
(b) involuntary and striated

Question 15.
Epithelium forming the peritoneal lining of the coelom is
(a) squamous epithelium
(b) cuboidal epithelium
(c) columnar epithelium
(d) glandular epithelium
Answer:
(a) squamous epithelium

Question 16.
Myelin sheath is a covering of
(a) vertebrate nerve fibre
(b) vertebrate muscle fibre
(c) insect nerve fibre
(d) ventricles of heart
Answer:
(b) vertebrate muscle fibre

Question 17.
Nature of dendrite is
(a) efferent
(b) afferent
(c) Both (a) and (b)
(d) None of these
Answer:
(c) Both (a) and (b)

Question 18.
Which type of connective tissue is a tendon?
(a) Dense
(b) Loose
(c) Fluid
(d) Skeletal
Answer:
(d) Skeletal

Question 19.
Intercalated disc is found in
(a) neuron
(b) skeletal muscle
(c) junction of muscle and nerve
(d) cardiac muscle
Answer:
(d) cardiac muscle

Question 20.
Larynx and trachea contain
(a) hyaline cartilage
(b) elastic cartilage
(c) bone
(d) fibrocartilage
Answer:
(a) hyaline cartilage

Question 21.
Myoglobin is found in
(a) white muscle fibre
(b) yellow fibre
(c) red muscle fibre
(d) All of these
Answer:
(c) red muscle fibre

Question 22.
Oil glands in mammal (rabbit) are found in
(a) epidermis of skin
(b) mucous epithelium of skin
(c) dermis of skin
(d) mucous epithelium of stomach
Answer:
(c) dermis of skin

Question 23.
Erythrocytes of frog are
(a) non-nucleated and biconcave
(b) nucleated biconvex
(c) nucleated biconcave
(d) non-nucleated biconvex
Answer:
(b) nucleated biconvex

Question 24.
Nerve cells develop from
(a) ectoderm
(b) mesoderm
(c) endoderm
(d) ectoderm and mesoderm
Answer:
(a) ectoderm

Question 25.
Mammary glands are
(a) apocrine
(b) holocrine
(c) merocrine
(d) None of these
Answer:
(a) apocrine

Question 26.
Cardiac muscle contracts
(a) quickly and is fatigued
(b) quickly and is not fatigued
(c) slowly and is not fatigued
(d) slowly and is fatigued
Answer:
(b) quickly and is not fatigued

Question 27.
Largest erythrocytes are found in
(a) man and monkey
(b) amphiuma and proteus
(c) fish and frog
(d) lizard and snake
Answer:
(c) fish and frog

Question 28.
Which vitamin is essential for blood clotting
(a) vitamin-A
(b) vitamin-C
(c) vitamin-K
(d) vitamin-E
Answer:
(c) vitamin-K

Question 29.
Blood transports
(a) oxygen only
(b) respiratory gases and excretory product only
(c) respiratory gases nutrients and excretory products
(d) respiratory gases and nutritive substances only
Answer:
(c) respiratory gases nutrients and excretory products

Question 30.
Lymph differs from blood in the
(a) absence of RBC
(b) absence of WBC
(c) excess of water
(d) absence of protein
Answer:
(a) absence of RBC

Question 31.
Blood is composed of
(a) plasma and corpuscles
(b) plasma and RBC
(c) plasma and WBC
(d) colloid particles
Answer:
(a) plasma and corpuscles

Question 32.
If RBCs are kept in distilled water they will
(a) contract
(b) just swell up
(c) remain unaffected
(d) swell up and burst
Answer:
(d) swell up and burst

Question 33.
RBCs are kept in 8% saline solution it will
(a) burst
(b) contract
(c) remain unaffected
(d) None of these
Answer:
(b) contract

Question 34.
RBC will contract if kept in
(a) isotonic solution
(b) distilled water
(c) hypertonic solution
(d) hypotonic solution
Answer:
(c) hypertonic solution

Question 35.
In 100 mL of blood of adult man amount of haemoglobin is
(a) 11 gm
(b) 12.5 gm
(c) 14 gm
(d) 20 gm
Answer:
(c) 14 gm

Question 36.
Red bone marrow occurs in
(a) ribs
(b) ribs and sternum
(c) ribs and cranium
(d) ribs, sternum and cranium
Answer:
(d) ribs, sternum and cranium

Question 37.
Secretion of sebaceous gland is
(a) holocrine
(b) apocrine
(c) epierine
(d) merocrine
Answer:
(a) holocrine

Question 38.
Which is a simple coiled tubular gland?
(a) Salivary gland
(b) Sweat gland
(c) Sebaceous gland
(d) Testes
Answer:
(b) Sweat gland

Question 39.
Haemopoietic tissue is
(a) dense connective tissue
(b) reticular tissue
(c) adipose tissue
(d) epithelial tissue
Answer:
(b) reticular tissue

Question 40.
Harmful bacteria and other foreign bodies are destroyed by
(a) plasma protein
(b) platelets
(c) phagocytosis by RBC
(d) phagocytosis by WBC
Answer:
(d) phagocytosis by WBC

Question 41.
Phagocytic cells in liver are
(a) Kupffer cell
(b) Chromaffin cell
(c) Mast cell
(d) None of these
Answer:
(a) Kupffer cell

Question 42.
Which is irregular in shape?
(a) RBC
(b) WBC
(c) Muscle fibre
(d) Epithelial cell
Answer:
(d) Epithelial cell

Question 43.
An erythrocyte in mammal is without nucleus because
(a) erythrocyte is not a cell
(b) nucleus is not required
(c) nucleus disappears during its formation
(d) nucleus is absent from the beginning
Answer:
(b) nucleus is not required

Question 44.
Source of energy for muscle contraction is
(a) actin
(b) myosin
(c) actomyosin
(d) ATP
Answer:
(d) ATP

Question 45.
Smooth muscles are
(a) involuntary, spindle-shaped uninucleate and tapering
(b) voluntary multinucleate and cylindrical
(c) involuntary cylindrical and multinucleate
(d) voluntary, branched and uninucleate
Answer:
(b) voluntary multinucleate and cylindrical

Question 46.
The fibrous connective tissue sheath of bones is known as
(a) pericardium
(b) perichondrium
(c) perineurium
(d) periosteum
Answer:
(d) periosteum

Question 47.
Sarcolemma is a membrane present on the outer side of
(a) nerve fibre
(b) bone
(c) muscle fibre
(d) RBC
Answer:
(c) muscle fibre

Question 48.
Tissue covering of the body surface is
(a) epithelial
(b) connective
(c) muscle
(d) adipose
Answer:
(a) epithelial

Question 49.
White matter of the spinal cord is made up of
(a) nerve cells
(b) non-myelinated nerve fibers
(c) myelinated nerve fibers
(d) connective tissue cells
Answer:
(c) myelinated nerve fibers

Question 50.
Haemopoiesis in adult human occurs in
(a) liver and spleen
(b) liver
(c) spleen
(d) red bone marrow
Answer:
(d) red bone marrow

Question 51.
In human, haemoglobin is present
(a) in the liver
(b) dissolved in the blood plasma
(c) in erythrocytes
(d) in spleen
Answer:
(c) in erythrocytes

Question 52.
Maximum number of cell bodies (cytons) are present in
(a) spinal cord
(b) retina
(c) brain
(d) ganglia
Answer:
(c) brain

Question 53.
If bone is kept in 5% KOH solution for some days.
(a) Be unaffected
(b) Dissolve
(c) Becomes soft and elastic
(d) Break
Answer:
(a) Be unaffected

Question 54.
Which salt is found in maximum quantity in bones?
(a) Calcium carbonate
(b) Calcium phosphate
(c) Sodium chloride
(d) Magnesium chloride
Answer:
(b) Calcium phosphate

Question 55.
If a bone is suspended in dilute hydrochloric acid, for a few days, it
(a) becomes harder
(b) becomes softer and malleable
(c) remains unaffected
(d) dissolves
Answer:
(b) becomes softer and malleable

Question 56.
Mast cells occur in
(a) nervous tissue
(b) connective tissue
(c) epithelial tissue
(d) skeletal tissue
Answer:
(b) connective tissue

Question 57.
Afferent nerve fibre carries nerve impulse
(a) from central nervous system to a receptor
(b) from receptor to the central nervous system
(c) from central nervous system to the effector organ
(d) from effector organs to the central nervous system
Answer:
(b) from receptor to the central nervous system

Question 58.
Increase in the number of erythrocytes is called
(a) polycythemia
(b) glycosuria
(c) hyperglycemia
(d) hypoglycemia
Answer:
(a) polycythemia

Question 59.
Epithelial tissue performs the following functions
(a) protection, secretion, absorption and respiration
(b) protection, secretion, sensation and absorption
(c) absorption, respiration, secretion and sensation
(d) All of the above
Answer:
(d) All of the above

Question 60.
The cells responsible for dissolving the bone matrix are called
(a) osteoblasts
(b) osteoclasts
(c) osteocytes
(d) chondrocytes
Answer:
(b) osteoclasts

Question 61.
Colourless plasma without corpuscles and fibrinogen is also known as
(a) chyle
(b) lymph
(c) serum
(d) thrombus
Answer:
(c) serum

Question 62.
Mammary glands are modified
(a) holocrine glands
(b) endocrine glands
(c) sebaceous glands
(d) sweat glands
Answer:
(d) sweat glands

Question 63.
Horns of a rhinoceros are composed of
(a) bone
(b) cartilage
(c) chitin
(d) keratin
Answer:
(d) keratin

Question 64.
A nerve is nothing, but a bundle of
(a) axons
(b) dendrites
(c) ganglia
(d) cell bodies
Answer:
(a) axons

Question 65.
Possible function of Nissl’s body is
(a) protein synthesis
(b) RNA synthesis
(c) RNA storage
(d) impulse conduction
Answer:
(a) protein synthesis

Question 66.
The male cockroach is identified by the presence of
(a) anal cerci
(b) long antennae
(c) anal styles
(d) wingless body
Answer:
(c) anal styles

Question 67.
In cockroach or insects the excretory organs are
(a) Malpighian tubules
(b) Nephridia
(c) Malpighian corpuscles
(d) Flame cells
Answer:
(a) Malpighian tubules

Question 68.
Cockroach is
(a) omnivorous
(b) sanguivorous
(c) insectivorous
(d) carnivorous
Answer:
(a) omnivorous

Question 69.
The juvenile stage of cockroach is known as
(a) larva
(b) pupa
(c) maggot
(d) nymph
Answer:
(c) maggot

Question 70.
In cockroach, the number of spiracles is
(a) 8 pairs
(b) 10 pairs
(c) 12 pairs
(d) 14 pairs
Answer:
(b) 10 pairs

Question 71.
The blood-filled cavity of cockroach is known as
(a) coelom
(b) haemocoel
(c) enteron
(d) pseudocoel
Answer:
(b) haemocoel

Question 72.
Cockroach respires by
(a) cuticle
(b) lungs
(c) trachea
(d) book lung
Answer:
(c) trachea

Question 73.
In cockroach, the main excretory product is
(a) ammonia
(b) urea
(c) uric acid
(d) hippuric acid
Answer:
(c) uric acid

Question 74.
Mouth parts of cockroach are of
(a) sponging type
(b) piercing type
(c) sucking type
(d) biting and chewing type
Answer:
(d) biting and chewing type

Question 75.
Muscles associated with heart of cockroach are
(a) pericardial muscles
(b) striped muscles
(c) tergo-sternal muscles
(d) alary muscles
Answer:
(d) alary muscles

Question 76.
The tubular heart of cockroach is composed of
(a) 6-chambers
(b) 9-chambers
(c) 10-chambers
(d) 13-chambers
Answer:
(d) 13-chambers

Question 77.
In cockroach nerve cord is
(a) single, ventral, solid
(b) double, ventral solid
(c) single, ventral, hollow
(d) double, ventral, hollow
Answer:
(b) double, ventral solid

Question 78.
Characters common in cockroach spider and prawn is
(a) book lungs
(b) jointed legs
(c) green glands
(d) compound eye
Answer:
(b) jointed legs

Question 79.
In cockroach the food is crushed and strained in
(a) crop
(b) gizzard
(c) mesenteron
(d) hepatic caecae
Answer:
(b) gizzard

Question 80.
Blood does not transport oxygen in
(a) bird
(b) earthworm
(c) rabbit
(d) cockroach
Answer:
(d) cockroach

Question 81.
How many chitinous teeth does the gizzard of cockroach have?
(a) 2
(b) 4
(c) 6
(d) 8
Answer:
(c) 6

Question 82.
In female cockroach the 7th sternum forms a boat-shaped structure called
(a) hypogynium
(b) gonapophyses
(c) phallomere
(d) podial plate
Answer:
(b) gonapophyses

Question 83.
Each ovary of cockroach is composed of
(a) 4 ovarioles
(b) 6 ovarioles
(c) 8 ovarioles
(d) 16 ovarioles
Answer:
(c) 8 ovarioles

Question 84.
Which of the following serves as the tongue of cockroach?
(a) Labium
(b) Maxillae
(c) Mandible
(d) Hypopharynx
Answer:
(d) Hypopharynx

Question 85.
Hepatic caeca in cockroach from
(a) junction of midgut and hindgut
(b) gizzard
(c) midgut
(d) junction of gizzard and midgut
Answer:
(c) midgut

Fill in the blanks with appropriate words

Question 1.
Lifespan of erythrocytes is ……………. days.
Answer:
120

Question 2.
Junction of two neurons is called ……………. .
Answer:
Synapse

Question 3
………… is the structural and functional unit of a muscle fiber.
Answer:
Sarcomere

Question 4
……………. are the longitudinal canals found in bone.
Answer:
Haversian canals

Question 5.
Nissl’s granules are found in …………….. .
Answer:
Cyton

Question 6.
Outer most layer of a cartilage is known as ……………. .
Answer:
Perichondrium

Question 7.
Bone forming cells are called ……………. .
Answer:
Osteoblasts

Question 8.
Cell bodies of most neurons in peripherial nervous system are grouped together as ……………. .
Answer:
Ganglion

Question 9.
Cartilage is formed by cells, called ……………. .
Answer:
Chondroblasts

Question 10.
……………… are periodic constrictions in the axon of a myelinated nerve fiber.
Answer:
Nodes of Ranvier

Question 11.
Branch of the science dealing with the study of tissues is known as ……………. .
Answer:
Anatomy

Question 12.
Brush border cuboidal epithelial cell possess ……………. at their free ends.
Answer:
Cilia

Question 13.
Plasma without fibrinogen is known as ……………. .
Answer:
Serum

Question 14.
A neuron receives the nerve impulse through ……………. and transmit it through ……………. .
Answer:
Dendrites, axon

Question 15.
Heart contains ……………. muscle.
Answer:
Cardiac

Question 16.
Transportation of ……………. is the main function of blood which is carried by a conjugate protein called ……………. .
Answer:
Oxygen, Haemoglobin

Question 17.
Epithelial tissue lining the blood vessel is known as ……………. .
Answer:
Endothelium

Question 18.
…………….. is the group of cells specialised to perform a specific function.
Answer:
Tissue

Question 19.
Haversian canal is found in ……………. .
Answer:
Bones

Answer each of the following in single word

Question 1.
Name a mammal having nucleated RBC.
Answer:
Camel

Question 2.
What type of cartilage is found in the intervertebral disc?
Answer:
Hyaline cartilage

Question 3.
Name the longest cell in the body?
Answer:
Neuron

Question 4.
Which animal possesses pneumatic bone?
Answer:
Birds

Question 5.
Who coined the term epithelium ?
Answer:
Raysch

Question 6.
Which muscle doesn’t get fatigued throughout life?
Answer:
Cardiac muscle

Question 7.
In which cell, Nissl granules are present?
Answer:
Neuron (cyton)

Question 8.
Volkman’s canal is present in which tissue?
Answer:
Bone

Question 9.
Who is known as father of histology?
Answer:
Xavier Bichat

Question 10.
Name the structural and functional unit of nervous tissue.
Answer:
Neuron

Question 11.
Name the tissue connecting muscle to a bone.
Answer:
Tendon

Question 12.
What is the expanded from of RBC?
Answer:
Red blood cell

Question 13.
Name the protein which constitutes the collagen fibre.
Answer:
Collagen

Question 14.
What type of cartilage is found in ear pinnae?
Answer:
Elastic cartilage

Question 15.
What type of tissue does blood come under?
Answer:
Connective tissue

Question 16.
Where are Schwann cells found?
Answer:
Axon

Question 17.
Which muscle is self excitatory?
Answer:
Cardiac muscle

Short Answer Type Questions

Answer each of the following within 50 words

Question 1.
What is a ligament?
Answer:
Ligament is the fibrous connective tissue that connects bones to other bones and is also known as articular ligament. They usually serves to hold structures together and keep them stable.

Question 2.
How would you obtain pavement epithelium?
Answer:
Simple sqamous epithelium is formed by a single layer of flat or spindle-shaped cells. The cells are closely fitted like the tiles on a floor with serrated edges. Therefore this epithelium is often known as pavement epithelium. Each cell contains a centrally placed spherical nucleus.

Question 3.
Why blood does not clot in blood vessel?
Answer:
Blood does not clot inside the body due to the presence of naturally occurring anticoagulant heparin, secreted by basophils and mast cells.

Question 4.
What is the advantage of having transitional epithelium in the wall of the urinary bladder?
Answer:
The number of cells in transitional epithelium changes with time. For example, the wall of the distended urinary bladder has 2-3 layers of cells. However when the bladder contracts, this number increases To 5-6. This is advantageous in having transitional epithelium in the wall of the urinary bladder.

Question 5.
What do you understand by pseudostratified epithelium?
Answer:
Pseudostratified Epithelium
The epithelium is one-cell thick, but appears 2-layered because all the cells do not reach the , . free surface. The cells are attached to the * basement membrane, hence they are called pseudostratified.
The mucus secreting goblet cells also occur in this epithelium.

Question 6.
What is the fundamental difference between spongy bone and compact bone?
Answer:
(a) Spongy (Cancellace) Bone it contains a ncrwork of thin and irrcgularly longitudinal and ransvcrsc bony bars called trabeculae covered by the cndosteum. it is found at che ends of long bones (epiphyses).
(b) Compact (Dense) Bone It is hard and compact and found in the shaft of long bones. It contains ydilow bone marrow and has Haversian systems.

Structure of cancellous (spongy) bone
(a) Spongy bone at the end of a long bone and
(b) microscopic structure of spongy bone

Question 7.
Name different types of leucocytes and enumerate their functions.
Answer:
The different types of leucocytes are

• Neutrophils They are attracted by chemotactic factors secreted by bacteria at the site of infection and acts as phagocytes and engulf and digest them.
• Eosinophils They are phagocytic cells with an affinity for antigen-antibody complexes formed at the site of inflammation and allergic reaction.
• Basophils These store histamine and heparin.
• Lymphocytes They play a key role in the immune response of the body.
• Monocyte They are phagdcytic in nature.

Question 8.
Why have tendons and ligaments more tensile strength?
Answer:
Tendon and ligaments are composed of dense connective tissue. These have densely packed collagen fibers. These cells are few and the ground substance is less. This gives them more tensile strength.

Question 9.
What do you mean by involuntary muscle?
Answer:
Involuntary muscles are muscles that contracts without conscious control and found in walls of internal organs such as stomach, intestine, bladder and blood vessels.

Question 10.
What is the difference between G-actin and F-actin?
Answer:
Actin forms microfilaments, it is globular and multifunctional protein. It is thus known as globular actin or G-actin. A G-actin molecule has an ATPase activity and a myosin head binding site. Several G-actins joins linearly forming a fibrous actin or f-actin. Two f-actins helically coil forming an actin filament.

Question 11.
Describe the role of troponin and tropomyosin in skeletal muscle contraction.
Answer:
Tropomyosin blocks myosin binding sites on actin molecules, preventing cross bridge formation, which prevents contraction in a muscle without nervous input. The protein complex troponin binds to tropomyosin, helping to position it on the actin molecule.

Question 12.
How does cardiac muscle differ from skeletal muscle?
Answer:
Difference between Skeletal muscle and Cardiac muscle

Skeletal muscle	Cardiac muscle
Attached to bones and cartilages.	Present in the wall of heart and the wall of large blood vessels in the vicinity of their entering or leaving the heart.
Voluntary and undergo fatigue.	Involuntary and never undergo fatigue.
Muscle fibers are long and cylindrical and never branch.	The fibers are branched. The branches anastomoise with each other.
The fibers are muitinucleated (syncytial).	The fibers are uninucleate, occasionally binucleated.
Intercalated dis.cs are absent.	Intercalated discs are present at the anastomosing points.

Question 13.
Name the cells, which from myelin sheaths in axons of central nervous system and peripheral nervous systems.
Answer:
Schwann cells forms myelin sheaths in axons of central nervous system and peripheral nervous system.

Question 14.
Name the macrophage associated with the nervous tissue. What is its function?
Answer:
Microglia are the smallest neuroglial cells. Their function is like that of macrophages of the connective tissue. When nervous tissue is damaged or injured, the microglial cells migrate to the site, proliferate and remove the debris by phagocytoses.

Write short notes on the following

Question 1.
Cartilage
Answer:
Cartilage
It is a tough, semitransparent, elastic and flexible tissue. The cartilage cells (chondrocytes) lie in groups of 2-3 in , fluid-filled spaces called lacunae. The cartilage is bounded externally by a stiff sheath called perichondrium containing white fibrous tissue. Cartilage is present in the tip of nose, outer ear joint, between adjacent bones of the vertebral column, limbs and hand in adults.

Question 2.
Bone of mammal
Answer:
Bone:
It is a hard and rigid connective tissue. These are non-pliable ground substance rich in calcium salts and collagen fibres providing strength to the bone. The cells of bone are found in a calcified matrix made up of ossein. The bone cells known as osteocytes are lodged in the spaces called lacunae.
They also interact with skeletal muscles attached to them to bring about movements.

A characteristic feature of mammalian bones are present in the matrix. Each Haversian canal contains an artery, a vein, a lymph vessel, a nerve and some bone cells.

Question 3.
Neuron
Answer:
Neurons are the functional unit of neural system. These are excitable cells. A neuron consists of a cell body (cyton) or soma and fine protoplasmic processes called neurites arising from the cell body.

Question 4.
Cardiac muscle
Answer:
Cardiac Muscles
The cardiac muscles are contractile tissues present only in the heart and in the wall of large veins which enter the heart. The cardiac muscle fibres show the characters of both unstriped and striped muscle fibres. Each fibre is a v long and cylindrical structure which has a definite – sarcolemma. The fibres are uninucleate and the nuclei lie near the centre.

Question 5.
Myofibril
Answer:
Myofibril It is also known as a muscle fibril. It is a basic rod-like unit of a muscle cell. Muscles are composed of tubular cells called myocytes, known as muscle fibres in striated and these cells in turn contain many chain of myofibrils.

Question 6.
Adipose tissue
Answer:
Adipose Tissue It is a modified type of areolar tissue. Its matrix contains large number of adipose cells along with fibrocytes and macrophages. White and yellow fibres are present in the matrix. The cells of this tissue are specialised to store fats.

The excess of nutrients which are not used immediately are converted into fats and are stored in this tissue. The adipose tissues are found in the subcutaneous region, around the heart, kidneys, eyeballs, etc. It is also found in the blubber of whales and elephants, hump of camel, fat bodies of frog and yellow bone marrow.

Loose connective tissue
(a) Areolar (b) A cell of adipose tissue

Question 7.
Stratified epithelium
Answer:
Stratified Compound Epithelia The stratified epithelia consist of many layers of cells. On the basis of the shape of the cells present in the superficial layers, the stratified epithelium are of four types
Stratified Squamous Epithelium The cells in the basal (deepest) layer are columnar or cuboidal with oval nuclei. It is called germinal layer. The cells in this region keep dividing by mitosis to form new cells.
The stratified squamous epithelium is further subdivided as two main types, i.e. keratinised and non-keratinised.

Question 8.
Neuroglia
Answer:
The neuroglia or glia cells are supporting cells which form a packing around the neurons in the brain, spinal cord and ganglia. Neuroglia make up more than one half the volume of neural tissue in our body. These cells have different shapes and many processes.
The neuroglia cells have various roles like myelin formation, transport of materials to neurons, maintenance of ionic balance and phagocytosis.

Question 9.
Haversian system
Answer:
Haversian System The osteon or Haversian system is the fundamental functional unit of much compact bone. Osteons are roughly cylindrical structures that are typically several millimeters long around 0.2 mm in diameter.

Question 10.
Leucocytes
Answer:
Leucocytes or White Blood Corpuscles (WBCs) lack haemoglobin and are colourless. They are nucleated with rounded or irregular shape. They can change their shape and are capable of amoeboid movement.

Question 11.
Sarcomere
Answer:
Sarcomere It is the basic unit of striated muscle tissue. It is the repeating unit between the two Z-lines. Skeletal muscles are composed of tubular muscle cells (myocytes called muscle fibres or myofibers), which are formed in a process known as myogenesis.

Differentiate between the following

Question 1.
Axon and Dendron
Answer:
Differences between dendrites and axons are

Dendrite	Axon
These are short fibres which branch repeatedly and project out of the cell body and also contain Nissl’s granules.	The axon is a long branched fibre, which terminates as a bulb-like structure called synaptic knob. It possesses synaptic vesicles containing chemicals called neurotransmitters.
These fibres transmit impulses towards the cell body.	The axons transmit nerve impulses away from the cell body to a synapse.
Its branches terminate into bulb like synaptic knobs.	Their branches do not have synaptic knobs.

Question 2.
Epithelial tissue and Connective tissue
Answer:
Difference between epithelial tissue and connective tissue are

Epithelial tissue	Connective tissue
The cells of a sub type are homogenous, e.g. squamous, columnar.	The cells of a sub type may be different, e.g. histiocytes, mast cells, adipose cells, etc.
Intercellular space is absent.	Large intercellular spaces are present.
It lies on basement membrane.	Basement membrane is absent.
The main functions of epithelial tissue are protection, secretion and perception of stimuli of different kinds.	To support organs and to provide connection between organs.

Question 3.
Cartilage and Bone
Answer:
Differences between bone and cartilage are

Bone	Cartilage
It is hard and inflexible.	It is comparatively soft and flexible.
The matrix contains ossein.	The matrix composes of chondrin.
Bone is highly vascular. Blood vessels occur in periosteum, endosteum marrow cavity, Haversian cannals and Volkmann’s canals.	Cartilage is largely a vascular. Vascular supply is limited to outer sheath or perichodrium.
It can be solid hollow or spongy.	It is always solid.
Osteocytes occur singly.	Chondrocytes may occur singly or in groups of 2-4.
Marrow is often present in the centre.	Marrow is absent.

Question 4.
Striated muscle and Non-striated muscle
Answer:
Difference between striated muscle and non-striated muscle

Striated muscle	Non-striated muscle
Striations present.	Striations absent.
it is voluntary in action.	It is involuntary in action.
The muscle fibres are long and cylindrical with blunt ends.	The muscle fibres are long spindle shaped with pointed ends.
The fibres are multinucleate.	The fibres are uninucleated.
Sarcoplasmic reticulum is well-developed.	Sarcoplasmic reticulum is poorly developed.
Sarcomeres present.	Sarcomeres absent.
Numerous mitochondria and glycogen are present.	Less mitochondria and glycogen granules are present.
Striated muscle is seen attached to skeleton.	Non-striated muscle is seen in internal organs.

Question 5.
Tendon and Ligament
Answer:
Differences between tendons and ligaments are

Tendons	Ligaments
The tendons are dense regular connective tissues, which attach the muscles to bones.	The ligaments are dense regular connective tissues, which attach the bones at the joints.
It is formed of white fibrous connective tissue.	It is formed of yellow elastic connective tissue.

Question 6.
Muscle cell and Nerve cell
Answer:
Difference between nerve cell and muscle cell are

Nerve cell	Muscle cell
It is the structural and functional unit of nervous tissue.	It is structural unit of muscle unit of nervous tissue.
It is specialised for transmission of impulses.	In addition to transmission of impulses, it involves in contraction and relaxation muscles.
Its plasma membrane is called neurolemma.	Its plasma membrane is called sarcolemma.
Its cytoplasm is called neuroplasm.	Its cytoplasm is called sarcoplasm.

Question 7.
Blood and Lymph
Answer:
Differences between blood and lymph are

Blood	Lymph
It contains plasma, erythrocytes, leucocytes and platelets.	It contains plasma and leucocytes.
The presence of haemoglobin imparts red colour to it.	It is colourless as haemoglobin is absent.
Its plasma contains more protein, and phosphorus as compared to lymph.	Its plasma has fewer protein and calcium less calcium and phosphorus than blood.
Contains moderate amount of CO2 and other metabolic wastes.	Contains excessive amount of CO2 and other metabolic wastes.

Question 8.
Cardiac muscle and Skeletal muscle
Answer:
Difference between Skeletal muscle and Cardiac muscle

Cardiac muscle	Skeletal muscle
Present in the wall of heart and the wall of large blood vessels in the vicinity of their entering or leaving the heart.	Attached to bones and cartilages.
Involuntary and never undergo fatigue.	Voluntary and undergo fatigue.
The fibers are branched. The branches anastomoise with each other.	Muscle fibers are long and cylindrical and never branch.
The fibers are uninucleate, occasionally binucleated.	The fibers are muitinucleated (syncytial).
Intercalated discs are present at the anastomosing points.	Intercalated dis.cs are absent.

Question 9.
Myelinated and Non-myelinated nerve fibre
Answer:
Differences between myelinated and non-myelinated nerve fibres are

Myelinated nerve fibre	Non-myelinated nerve fiber
The myelinated nerve fibres are enveloped with Schwann cells, which form a myelin sheath around the axon.	Non-myelinated nerve fibres are enclosed by a Schwann cell that does not from a myelin sheath around the axon.
Myelinated nerve fibres are found in spinal and cranial nerves.	These are commonly found in autonomous and the somatic nervous systems.

Question 10.
RBC and WBC
Answer:
Difference between RBC and WBC are

RBC (Erythrocytes)	WBC (Leucocytes)
RBCs are small, circular, biconcave and non-nucleate cells.	Larger than RBC, amoeboid and nucleated cells.
Red due to the presance of haemoglobin.	Colourless due to the absence of haemoglobin.
More numerous than WBCs i.e. vary from 4.5 to 5.5 millions/ mm³.	Less numerous than . RBC- i.e. vary from 8000 to 10000 mm³.
Lifespan is approximately 120 days.	Lifespan is only a few days.
Carry molecules oxygen from the lungs to the tissues.	Mostly defend the body from external aggression.

Question 11.
Areolar tissue and Adipose tissue
Answer:
Difference between areolar tissue and adipose tissue are

Areolar tissue	Adipose tissue
Areolar tissue is mainly connective.	It is a mainly concerned with the storage of fat.
It usually fixes skin with the muscles.	The cells are spherical or oval and are packed in a matrix.
It forms packaging of the material in all organs between the muscles.	The matrix of the tissue consists of fibroblasts, macrophages and collagen fibres.
It has two types of fibres white and yellow.	It is found around the kidneys, blood vessels and also heart.

Odisha State Board CHSE Odisha Class 11 Biology Solutions Chapter 6 Anatomy of Flowering Plants Textbook Questions and Answers.

CHSE Odisha 11th Class Biology Chapter 6 Question Answer Anatomy of Flowering Plants

Anatomy of Flowering Plants Class 11 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Fill in the blanks

Question 1.
Companion cells are associated with …………… .
Answer:
Sieve elements

Question 2.
Numerous vascular bundles are scattered in the ground tissue of …………. stem.
Answer:
Monocot

Question 3.
Vascular bundles in which phloem is found on both sides of xylem are called …………. .
Answer:
Bicollateral

Question 4.
The inner, darker and harder portion of secondary xylem that cannot conduct water in an older stem is called ………. wood.
Answer:
Heart

Write True or False. Then correct the sentences without changing the underlinked worlds

Question 1.
Conjoint vascular bundles are those in which xylem and phloem occur in one strand.
Answer:
True

Question 2.
In maize stem bicollateral vascular bundles are seen.
Answer:
In Cucurbita stem bicollateral vascular bundles are seen.

Question 3.
Vascular tissue system develops from ground meristem.
Answer:
Vascular tissue system develops from procambium.

Question 4.
Epidermal tissue system originates from protoderm.
Answer:
True

Question 5.
Endodermis is the outer Layer of stele.
Answer:
Pericycle is the outer Layer of stele.

Question 6.
Outer layer of tunica always gives rise to epidermis.
Answer:
True

Question 7.
Bulliform cells belong to epidermal tissue system.
Answer:
True

Question 8.
Epistomatic leaves are generally found in hydrophytes.
Answer:
True

Question 9.
Casparian strips are seen in pericycle layer.
Answer:
Casparian strips are seen in hypodermis.

Question 10.
Starch sheath refers to cells of pericycle with starch.
Answer:
Starch sheath refers to cells of endodermis with starch grains.

Short Answer Type Questions

Differentiate between the following

Question 1.
Spongy parenchyma and palisade parenchyma
Answer:
Differences between palisade and spongy parenchyma are

Palisade Parenchyma	Spongy Parenchyma
These are present below the upper epidermis in dorsiventral leaf.	These are present towards the lower epidermis in dorsiventral leaf.
These are vertically elongated parenchymatous cells and are tightly fitted to each other without intercellular spaces.	These are oval-shaped parenchymatous cells and are loosely arranged with large air chambers.
These are present in three layers.	These are present in multilayers.
These cells contain more chloroplasts, which are radially arranged in these cells. Thus, the upper part of the leaf is dark green.	These cells contain few chloroplasts, which are irregularly distributed. Thus, lower part of the leaf is less green.

Question 2.
Vascular bundles of Maize and Tridax
Answer:
Differences between vascular bundles of maize and Tridax are

Vascular bundles of Maize	Vascular Bundles of Tridax
Maize is a monocot.	Tridax is a dicot
In stem	In stem
Vascular bundles are scattered in the ground tissue system.	Vascular bundles are arranged in a ring.
Vascular bundles are comparatively more in number.	Vascular bundles are fewer in number.
Vascular bundles are elliptical or rounded.	Vascular bundle are wedge shaped.
Vascular bundles are open.	Vascular bundles are closed.
Vascular bundle are not surrounded by any bundle sheath.	Vascular bundles are
In Root	In Root
Vascular bundles are polyarch and radial.	Vascular bundles are four in number arranged on alternate radii.

Question 3.
Heartwood and sap wood.
Answer:
Differences between sapwood and heartwood are

Sapwood	Heartwood
The outer region of the old trees forms the sap wood.	The central region of the old trees forms the heart wood.
It is also called as alburnum.	It is also called as duramen.
It is soft and not durable.	It is hard and durable.
It is light coloured and formed of living cells.	It is dark coloured due to the deposition of various substances.
Vessels are not blocked by tyloses.	Vessels are blocked by tyloses with various deposits.
The function of this region is conduction of water and nutrients and also storage of food.	The function of this region is mechanical support.

Question 4.
Permanent tissue and meristematic tissue.
Answer:
Differences between meristematic and permanent tissues

Meristematic tissue	Permanent tissue
Continuously dividing cells.	Do not divide continuously
Cells are small and isodiametric	Variable in shape and size
Cell wall is thin	Cell wall is thick
Nuclei are large	Nuclei are small
Vacuoles are absent	Vacuoles are present
Intercellular spaces absent	Intercellular spaces present
Metabolic activities are at high rate	Low rate
Inorganic inclusion absent	Present
Cell are undifferentiated	Cells are differentiated
Simple tissue	Simple or complex

Question 5.
Spring wood and autumn wood.
Answer:
Differences between spring wood and autumn wood are

Spring wood (Early wood)	Autumn wood (Late wood)
1. Wood formed in favourable season is called spring wood.	Wood formed in unfavourable season is called autumn wood.
2. The band of xylem is broad.	The band of Xylem is narrow.
3. Xylem has wider lumen and thin walled vessels.	Xylem has narrower lumen with thick walled vessels
4. Lighter in colour.	Comparatively darker
5. Fibres are less in number	Fibers are abundant.

Question 6.
Cork and bark.
Answer:
Differences between cork and bark are

Cork	Bark
1. Cork is a part of bark arising through the division of cork cambium.	Bark is the protective; outer layer of a woody tree.
2. Cork is formed through cork cambium.	Bark is formed through both cork and vascular cambium. Bark consists of the cork, cork cambium and the secondary phloem.
3. Cork consists of dead cells, which are filled with suberin.	Bark contains live tissues like cork cambium and secondary phloem.

Write note on

Question 1.
Cambium
Answer:
Formation of Cambium Ring
The parenchyma cells of the primary medullary rays adjacent to the intrafascicular cambium undergo dedifferentiadon and give rise to interfascicular cambium.
This joins the intrafascicular cambium of either side to form a complete ring of meristem called the cambium ring.

Question 2.
Lateral meristem
Answer:
Lateral Meristems:
The meristems that occur in the mature regions of roots and shoots of many plants. These meristems produce woody axis. These appear later than primary meristem, so are also called the secondary meristem.
They are cylindrical meristems. Some examples of lateral meristems are fascicular vascular cambium, interfascicular cambium and cork cambium. These are responsible for producing the secondary tissues.

Question 3.
Bark
Answer:
Bark:
Bark is a non-technical term used to describe all tissues exterior to the vascular cambium, therefore including secondary phloem. The bark refers to a number of tissues, i.e., periderm and secondary phloem. The bark that is formed early in the season is called early or soft bark. Towards the end of the season, late or hard bark is formed.

Question 4.
Lenticels
Answer:
Lenticels:
At certain regions of stem, the phellogen cuts off closely arranged parenchymatous cells on the outer side instead of cork cells.
These parenchymatous cells soon rupture the epidermis forming a lens-shaped opening called lenticels. The lenticels are mostly found in woody trees.

Question 5.
Hydathode
Answer:
These are specialised pores along the margins and apex of the leaf through which the secretion of water (guttation) takes place. Hydathodes or water stomata consists of vein endings, epithem chamber and pores. Pores are surrounded by guard cells, but remains open permanently.

Question 6.
Promeristem
Answer:
Procambium:
Ir develops into primary vascular tissue. It forms the isolated strands of elongated cells, very near to the central region.

Question 7.
Glandular tissues.
Answer:
Glandular Tissues These have unicellular or multicellular glands, which may secrete or excrete chemicals. They are present either externally or internally.

1. External glands are superficial in nature and formed on epidermis. They may occur as hydathodes glandular hairs, nectaries and digestive glands, etc.
2. Internal glands are confined to internal tissues.
   They are formed by lysis of some of the cells or by splitting of cells at middle lamella. They occur as oil glands, mucilage secreting glands, etc.

Question 8.
Annual ring.
Answer:
In tropical areas, the growth of secondary xylem is continuous. In others, yearly growth is very distinct and appears in the form of annual rings.

The transition from springwood to autumnwood is gradual. After autumnwood and before springwood of next year, there is no growth.
Therefore, change over from autumnwood to springwood is sudden.

The light coloured springwood and its next dark coloured autumnwood constitutes an annual ring or growth ring. It represents the total secondary xylem or wood formed in one year.

Question 9.
Different types of stomata
Answer:
The stomata (sing, stoma) are openings in the epidermis of most of the aerial parts of the plants, especially the leaves. Each stomata is composed of two bean-shaped cells called as guard cells, which enclose stomatal pore. The guard cells are generally much smaller in size as compared to other epidermal cells.

They are sensitive to even a small change in turgor pressure. The dimension of stomatal pore varies from species to species, but it measures about 20 Jim in length and about 10-20 jlm in width when fully open.

In some species, the guard cells are surrounded by subsidiary cells or accessory cells which differ morphologically from the other epidermal cells. The guard cell walls have special elastic properties. The adjoining cell walls of two guard cells around pore are free and not attached with each other.

These properties help them to stretch laterally during stomatal opening. The stomatal aperture, guard cells and the surrounding subsidiary cells are together called stomatal apparatus.

In most monocots, the guard cells are dumb-bell-shaped. The stomata are mostly found on the upper epidermis of the leaves. In some hydrophytes, the stomata occur on the upper surface to avoid water contact.

Question 10.
Trichomes
Answer:
Trichomes The epidcrmal hairs present on the stem are called trichomes. These are epidermal outgrowths present temporarily or permanently on almost all plant parts. They are multicellular structures which may he branched or unbranched. They may be secretory in nature.
They also help in checking the rate of transpiration from aerial plant surfaces.

Long Answer Type Questions

Question 1.
Compare the internal structure of a dicot stem with that of a dicot root.
Answer:
Dicotyledonous Stem:
The transverse section (TS) of a typical young dicotyledonous stem (e.g. Halianthus annus, Cucurcubita maxima, etc.) shows the following areas

Epidermis:
The outermost protective layer of the stem is called epidermis. It is covered with a thin-layer of cudcle and may bear trichomes and a few stomata.
The cuticle protects the tissues from injury as well as diseases from the entry of fungal spores and bacteria. It also helps to prevent loss of water.
Epidermal Epidermis Hypodermis Parenchyma Endodermis Pericycle Vascular bundle Medullary rays

Cortex:
This layer lies just below the epidermis and extends till ” endodermis. Its various parts are hypodermis, general cortex and endodermis.
(i) Hypodermis
It is just below the epidermis consisting of collenchymatous cells. The cells contain chloroplasts. It provides mechanical strength to the stem.
(ii) General Cortex
It is located just below the hypodermis and consists of a few layers of parenchymatous cells. These cells are thin-walled have big intercellular spaces and may contain chloroplasts.
(iii) Endodermis
It lies just beneath the general cortex in the form of single layer of barrel-shaped cells surrounding the stele. It is the innermost layer of cortex. In sunflower, it contains starch, hence is called starch sheath.

Dicotyledonous Root:
The primary internal structure of dicot root (e.g. gram) can be studied from the Transverse Section (TS) of a young root of sunflower, pea or gram. The primary root is the one which has only primary permanent tissues that are formed from vegetative shoot apex. Secondary tissues are absent.
The following structures can he seen from periphery towards the centre
Epidermis:
It forms the outermost layer in young root. It is equivalent to epidermis of stem. The stomata and cuticle are not present in it. The cells are thin-walled and tubular. Some of the epidermal cells are prolonged to form thin-walled tubular structures called root hairs. The cells which produce root hair are called root hair cells or trichoblasts. Due to the presence of root hairs, epiblema is also called piliferous layer (Pilus – hair; ferre – to carry) and rhizodermis (Rhiza – root; derma – skin).

TS of a typical dicot root

Root hairs have pectose layer on the outside, this is to help them to pass into the soil spaces for absorption of water and mineral salts. The active lifespan of root hairs is upto 7 days and they die off in older parts of the root.
The cells of older epidermis shrivel afterwards and become cutinised and suberised.

Cortex:
It lies beneath the epiblema. It consists of several layers of thin-walled parenchymatous cells with conspicuous intercellular spaces. The cells of cortex store food. It also conducts water from the epiblema to the inner tissues.

Endodermis:
The innermost layer of the cortex is endodermis. It comprises of a single layer of barrel-shaped cells without any intercellular spaces. The endodermal cells are living and are rich in starch grains.

They have characteristic bands of thickenings along their radial and tangential walls. These are called casparian bands or casparian strips.
The casparian strips are made up of suberin and lignin. These strips prevent plasmolysis of endodermal cells and do not allow wall to wall movement of substances, between cortex and pericycle.

The cells of endodermis lying opposite to the protoxylem are thin-walled to permit free passage of water and minerals from cortex into the xylem. These are called passage cells.

Question 2.
Describe the anatomy of a typical monocot stem with labelled diagram. Point out the differences in the structure of vascular bundles in monocot stem and dicot stem.
Answer:
Monocotyledonous Stem:
The monocot stem (e.g. Zea mays, Canna, etc.) possesses only primary structure. The different monocot stems from outside towards inside consist of epidermis, hypodermis, ground tissue and vascular system.

Epidermis:
It is single-layered, having stomata in it. The cells have a thick cuticle layer on the outside.

TS of monocot stem

Hypodermis
It is 2-3 layered having lignified scierenchymatous cells present just below the epidermis.

Ground Tissue
It fills the whole interior of the stem containing parenchymatous cells. A number of vascular bundles are scattered in it.

Vascular System
Monocot stems has scattered vascular bundles.
Each vascular bundle in vascular strand is surrounded by a sheath of sclerenchyma known as bundle sheath cells. The vascular bundles possess both phloem (phloem parenchyma is absent) and xylem, so these are conjoint type.

The bundles are endarch with the protoxylem and metaxylem are arranged in the form of a ‘Y’. The divergent ends are occupied by two pitted vessels and convergent end by two smaller spiral vessels lying radially in the centre. A water containing cavity called lysigenous cavity is present in association with the protoxylem.

It is formed by the breakdown of inner protoxylem vessels and parenchyma during the earlier stages of growth. The cavity is absent or reduced in the smaller vascular bundles that occur in contact with sclerenchymatous hypodermis.
A brief account of internal structure of Zea mays and Canna has been described here under.

Differences between vascular bundles in monocot stem

Vascular Bundle in Monocot Stem	Vascular Bundle in Dicot Stem
Vascular bundles are arranged in a ring. This is called stelar region.	Vascular bundles are scattered in the ground tissue system.
Vascular bundles are fewer in number.	Vascular bundles are comparatively more in number.
Vascular bundles are wedge-shaped.	Vascular bundles are elliptical or rounded.
Vascular bundles are surrounded by bundle sheath	Vascular bundles are not surrounded by any bundle sheath.
Vascular bundles are closed	Vascular bundles are open.