BSE Odisha 10th Class Maths Notes Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି

Odisha State Board BSE Odisha 10th Class Maths Notes Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି will enable students to study smartly.

BSE Odisha Class 10 Maths Notes Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି

→ କାର୍ଟେଜୀୟ ସମତଳ ଓ କାର୍ଟେଜୀୟ ସ୍ଥାନାଙ୍କ (Cartesian Plane and Cartesian Co-ordinates) :

→ବିଷୟବସ୍ତୁର ରୂପରେଖ

• କାର୍ଟେଜୀୟ ସମତଳ ଓ କାର୍ଟେଜୀୟ ସ୍ଥାନାଙ୍କ
• ଦୁଇଟି ଦତ୍ତ ବିନ୍ଦୁ ମଧ୍ୟରେ ଦୂରତ ।
• ବିଭାଜନ ସୂତ୍ର
• ତ୍ରିଭୁକର କ୍ଷେତ୍ରଫଳ

→ ଯେକୌଣସି ବାସ୍ତବ ସଂଖ୍ୟା ଏକ ସରଳରେଖା ଉପରେ ଗୋଟିଏ ବିନ୍ଦୁଦ୍ୱାରା ସୂଚିତ ହୋଇପାରିବ ଏବଂ ବିପରୀତ କ୍ରମେ ସରଳରେଖାର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁ ଏକ ବାସ୍ତବ ସଂଖ୍ୟାଦ୍ବାରା ସୂଚିତ ହୋଇପାରିବ । କିନ୍ତୁ ଉକ୍ତ ସରଳରେଖାର ବାହାରେ, ସମତଳ ଉପରେ ଅବସ୍ଥିତ କୌଣସି ବିନ୍ଦୁକୁ ଗୋଟିଏ ସଂଖ୍ୟା ସାହାଯ୍ୟରେ ସୂଚିତ କରାନଯାଇ ଦୁଇଟି ବାସ୍ତବ ସଂଖ୍ୟାଦ୍ଵାରା ସୂଚିତ କରାଯାଏ ।

→ ଏଠାରେ ଆମେ ଦୁଇଗୋଟି ସଂଖ୍ୟାରେଖା \(\overleftrightarrow{\mathbf{X’OX}}\) ଓ \(\overleftrightarrow{\mathbf{Y’OY}}\) ନେବା ଯେପରିକି ସେମାନେ ସମକୋଣରେ ପରସ୍ପରକୁ ଠ ବିନ୍ଦୁରେ ଛେଦ କରିବେ । \(\overleftrightarrow{\mathbf{X’OX}}\) ଓ \(\overleftrightarrow{\mathbf{Y’OY}}\) ସଂଖ୍ୟାରେଖା ଦ୍ଵୟକୁ ଯଥାକ୍ରମେ x-ଅକ୍ଷ (x- axis) ଓ y-ଅକ୍ଷ (y-axis) କୁହାଯାଏ ଏବଂ O ବିନ୍ଦୁକୁ ମୂଳବିନ୍ଦୁ (Origin) କୁହାଯାଏ । ଯେହେତୁ ଏହି ସମତଳଟି ଦୁଇଟି ବାସ୍ତବ ସରଳରେଖା ଦ୍ୱାରା ସୂଚିତ ହୁଏ, ତେଣୁ ଏହାକୁ R × R ବା R² -ସମତଳ (R² – Plane) ମଧ୍ୟ କୁହାଯାଏ । ଏହି ଅକ୍ଷଦ୍ବୟ R’-ସମତଳକୁ ଚାରିଭାଗରେ ବିଭକ୍ତ କରେ । ପ୍ରତ୍ୟେକ ଭାଗକୁ ପାଦ (Quadrant) କୁହାଯାଏ । ପ୍ରଥା ଅନୁସାରେ XOY ପାଦକୁ ପ୍ରଥମ ପାଦ (First quadrant, Q₁), YOX’ କୁ ଦ୍ଵିତୀୟ ପାଦ (Second quadrant, Q₂), X′OY’ କୁ ଦ୍ଵିତୀୟ ପାଦ (Third quadrant, Q₃) ଓ Y’OXକୁ ଚତୁର୍ଥ ପାଦ (Fourth quadrant, (Q₄) କୁହାଯାଏ ।

→ ମନେକର କାଗଜର ଉପର ପୃଷ୍ଠତଳ ଆମର ଆଲୋଚ୍ୟ ସମତଳ ଓ ଏହି ସମତଳ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ P ର ଅବସ୍ଥିତି ନିରୂପଣ କରିବା । P ବିନ୍ଦୁରୁ x-ଅକ୍ଷ ପ୍ରତି PM ଲମ୍ବ ଓ y-ଅକ୍ଷ ପ୍ରତି PN ଲମ୍ବ ଅଙ୍କନ କର । ଯଦି x-ଅକ୍ଷର ଅବସ୍ଥିତି M ବିନ୍ଦୁ ବାସ୍ତବ ସଂଖ୍ୟା xକୁ ସୂଚାଏ ଏବଂ y-ଅକ୍ଷରେ ଅବସ୍ଥିତି N ବିନ୍ଦୁ ବାସ୍ତବ ସଂଖ୍ୟା yକୁ ସୂଚାଏ, ଅର୍ଥାତ୍ OM = NP = x ଏବଂ ON =MP = y, ତେବେ ଆମେ P ବିନ୍ଦୁକୁ ଦୁଇଟି କ୍ରମିତ ଯୋଡ଼ି (ordered pair) (x, y) ଦ୍ଵାରା ସୂଚିତ କରିପାରିବା ଏବଂ ଲେଖୁଲାବେଳେ ଆମେ ଏହାକୁ P(x, y) ଦ୍ଵାରାପ୍ରକାଶ କରିବା ।

→ ବାସ୍ତବ ସଂଖ୍ୟା xକୁ P ବିନ୍ଦୁର x-ସ୍ଥାନାଙ୍କ (x-co-ordinate) ବା ଭୁଜ (abscissa) ଏବଂ ବାସ୍ତବ ସଂଖ୍ୟା yକୁ P ବିନ୍ଦୁର y ସ୍ଥାନାଙ୍କ (y-coordinate) ବା କୋଟି (ordinate) ବୋଲି କୁହାଯାଏ ।

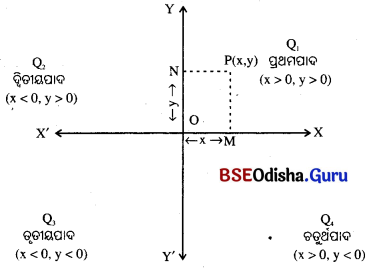
→ P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଦ୍ଵୟ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ କ୍ରମରେ (ପ୍ରଥମ x ଓ ପରେ y) ଆବଦ୍ଧ ହେଉଥ‌ିବାରୁ ଏହାକୁ ଏକ କ୍ର ମିତ ସଂଖ୍ୟାଯୋଡ଼ି (ordered pair) ବୋଲି କୁହାଯାଏ । ତେଣୁ କୌଣସି ବିନ୍ଦୁ ସ୍ଥାନାଙ୍କର ପ୍ରଥମ ସଂଖ୍ୟାଟି x ଓ ଦ୍ବିତୀୟ ସଂଖ୍ୟାଟି y-ସ୍ଥାନାଙ୍କକୁ ବୁଝାଏ ।

ସର୍ବପ୍ରଥମେ ସ୍ଥାନାଙ୍କଦ୍ୱାରା ସୂଚିତ କରାଯାଇଥିବା ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତିର ଜନକ ଡେକାର୍ଟେଙ୍କ ନାମାନୁସାରେ P ବିନ୍ଦୁର ଏହି ସ୍ଥାନାଙ୍କକୁ କାର୍ଟେଜୀୟ ସ୍ଥାନାଙ୍କ (Cartesian co-ordinates) କୁହାଯାଏ । ବସ୍ତୁଟି ଯେଉଁ ସମତଳରେ ଅବସ୍ଥିତ, ସେ ସମତଳକୁ କାର୍ଟେଜୀୟ ସମତଳ (Cartesian Plane) କୁହାଯାଏ !

→ ସମତଳ :

• ସମତଳଟି ଅସଂଖ୍ୟ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍ । ସ୍ଥାନାଙ୍କ ସମତଳରେ ପ୍ରତ୍ୟକ ବିନ୍ଦୁପାଇଁ ଏକ କ୍ରମିତ ସଂଖ୍ୟାଯୋଡ଼ି ରହିଛି । ତେଣୁ ସେଟ୍ ଭାଷାରେ ସମତଳକୁ ଲେଖିଲେ-
  ସମତଳ = {(x, y) | x, y ∈ R}
• (x, y) ∈ R × R ବା R² । ତେଣୁ ଏହି ସ୍ଥାନାଙ୍କ ସମତଳକୁ R-ସମତଳ (R-Plane) ବା କାର୍ଟେଜୀୟ ସମତଳ (Cartesian Plane) ମଧ୍ୟ କୁହାଯାଏ ।
  A × B = {(a, b) | a ∈ A, ∈ B}
  B × A = {(b, a) | a ∈ A, ∈ B}
  ଯଦି A = B = R (ବାସ୍ତବ ସଂଖ୍ୟା ସେଟ୍) ତେବେ କାର୍ଟେଜୀୟ ଗୁଣଫଳ ସେଟ୍ R × R = {(x, y) | x, y = R} ଓ ଏହାକୁ R? ରୂପେ ମଧ୍ୟ ଲେଖାଯାଏ ।

→ \(\overleftrightarrow{\mathbf{X’OX}}\) ଅକ୍ଷର \(\overrightarrow{\mathrm{OX}}\) କୁ x-ଅକ୍ଷର ଧନଦିଗ, \(\overrightarrow{ OX’ } \) କୁ ଋଣଦିଗ କୁହାଯାଏ । ସେହିପରି \(\overrightarrow { OY } \) ଏବଂ \(\overrightarrow{ OY’ } \) କୁ \(\overleftrightarrow{\mathbf{Y’OY}}\) ଅକ୍ଷର ଯଥାକ୍ରମେ ଧନଦିଗ ଓ ଋଣଦିଗ ଭାବେ ନିଆଯାଇଥାଏ ।

→ପ୍ରଥମେ x-ଅକ୍ଷରେ ଅବସ୍ଥିତ ଯେକୌଣସି ଏକ ବିନ୍ଦୁ Mର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କରାଯାଉ । ଏହାର x-ସ୍ଥାନାଙ୍କ x ଏବଂ y-ସ୍ଥାନାଙ୍କ ଶୂନ । କାରଣ x-ଅକ୍ଷଠାରୁ \(\overrightarrow{ OY } \) ବା \(\overrightarrow{ OY’ } \) ଦିଗରେ M ବିନ୍ଦୁର ଦୂରତା ଶୂନ ହୋଇଥିବାରୁ ଏହାର y-ସ୍ଥାନାଙ୍କ ଶୂନ ।

• ତେଣୁ x- ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ଯେକୌଣସି ବିଦୁର ସ୍ଥାନାଙ୍କ (x, 0) ଅର୍ଥାତ୍ x-ଅକ୍ଷର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁର y-ସ୍ଥାନାଙ୍କ = 0 ।
• ସେହିପରି y- ଅକ୍ଷର ଯେକୌଣସି ବିଦୁର ସ୍ଥାନାଙ୍କ (0, y) ଅର୍ଥାତ୍ y-ଅକ୍ଷର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁର x ସ୍ଥାନାଙ୍କ 0 ।
• ମୂଳବିନ୍ଦୁ ( ଉଭୟ ଅକ୍ଷର ପରସ୍ପର ଛେଦବିନ୍ଦୁରେ ଥିବାରୁ ଏହାର ସ୍ଥାନାଙ୍କ (0, 0) ଅଟେ ।
  • ପ୍ରଥମ ପାଦରେ ଅବସ୍ଥିତ ଯେକୌଣସି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ପାଇଁ x > 0, y > 0 । ଅର୍ଥାତ୍‌x ଓ y ଉଭୟେ ଧନାତ୍ମକ ।
  • ଦ୍ଵିତୀୟ ପାଦରେ ଅବସ୍ଥିତ ଯେକୌଣସି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ପାଇଁ x < 0, y > 0 ଅର୍ଥାତ୍ x ଋଣାତ୍ମକ ଓ y ଧନାତ୍ମକ ।
  • ତୃତୀୟ ପାଦରେ ଅବସ୍ଥିତ ଯେକୌଣସି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ପାଇଁ x < 0, y < 0 । ଅର୍ଥାତ୍‌ x ଓ y ଉଭୟେ ଋଣାତ୍ମକ ।
  • ଚତୁର୍ଥ ପାଦରେ ଅବସ୍ଥିତ ଯେକୌଣସି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ପାଇଁ x > 0, y < 0 । ଅର୍ଥାତ୍‌ x ଧନାତ୍ମକ ଓ y ଋଣାତ୍ମକ ।
• ଅକ୍ଷଦ୍ବୟ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁ କୌଣସି ପାଦରେ ଅନ୍ତର୍ଭୁକ୍ତ ନୁହଁନ୍ତି ।
• x- ଅକ୍ଷର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁର y-ସ୍ଥାନାଙ୍କ (0) ହେତୁ x-ଅକ୍ଷର ସମୀକରଣ ହେଉଛି y = 0 ।
  ସେହିପରି y- ଅକ୍ଷର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁର x-ସ୍ଥାନାଙ୍କ ( ହେତୁ y-ଅକ୍ଷର ସମୀକରଣ ହେଉଛି x = 0 ।

→ ଦୁଇଟି ଦତ୍ତ ବିନ୍ଦୁ ମଧ୍ୟରେ ଦୂରତ | (Distance between two given points) :

• ଉପପାଦ୍ୟ 1 :
  
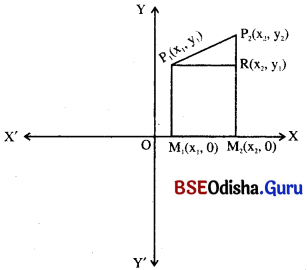
• ସ୍ଥାନାଙ୍କ ସମତଳରେ P₁(x₁, y₁) ଓ P₂(x₂, y₂) ଦୁଇଟି ଦତ୍ତ ବିନ୍ଦୁ ହେଲେ, ସେମାନଙ୍କ ଦୂରତା
  P₁P₂ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) ବା \(\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\)
• ଦତ୍ତ : ସ୍ଥାନାଙ୍କ ସମତଳରେ P₁(x₁, y₁) ଏବଂ P₂(x₂, y₂) ଦୁଇଟି ବିନ୍ଦୁ ।
• ପ୍ରାମାଣ୍ୟ : P₁P₂ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)
• ଅଙ୍କନ : ଏକ ସମତଳରେ P₁ ଓ P₂ ଦୁଇଟି ବିନ୍ଦୁ । ସେମାନଙ୍କର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (x₁, y₁) ଓ (x₂, y₂) । P₁P₂ ରେଖାଖଣ୍ଡ ଅଙ୍କନ କର ।
  P₁ ଓ P₂ ବିଦୁ୍ୟଦ୍ବୟରୁ x-ଅକ୍ଷ ପ୍ରତି ଯଥାକ୍ରମେ \(\overline{{P}_1 {M}_1}\) ଓ \(\overline{{P}_2 {M}_2}\) ଲମ୍ବ ଅଙ୍କନ କର । ପୁନଶ୍ଚ, P₁ ବିନ୍ଦୁରୁ P₂M₂ ପ୍ରତି x-ଅକ୍ଷ ସହ ସମାନ୍ତର କରି PAR ରେଖାଖଣ୍ଡ ଅଙ୍କନ କର ।
• ପ୍ରମାଣ : OM₁ = x₁, OM₂ = x₂, M₁P₁ = y₁ ଓ M₂P₂ = y₂
  ତେଣୁ P₁R = M₁M₂ = OM₂ – OM₁ = x₂ – x₁
  ଏବଂ RP₂ = M₂P₂ – M₂R = M₂P₂ – M₁P₁ = y₂ – y₁
  ଯେହେତୁ ∆ P₁RP₂ ରେ m∠P₁RP₂ = 90°
  ତେଣୁ ପିଥାଗୋରାସ୍ ଉପପାଦ୍ୟ ଅନୁସାରେ (P₁P₂)² = (P₁R)² + (RP₂)²= (x₂ – x₁)² + (y₂ – y₁)²
  ଯେହେତୁ ଦୂରତା ଏକ ଧନାତ୍ମକ ସଂଖ୍ୟା ।
  ତେଣୁ P₁P₂ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) ଅଥବା \(\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\)
  

→ ଅନୁସିଦ୍ଧାନ୍ତ 1 : ମୂଳବିନ୍ଦୁ O(0, 0)ରୁ ଯେକୌଣସି ବିନ୍ଦୁ P(x, y) ର ଦୂରତା OP = \(\sqrt{x^2 + y^2}\) ହେବ ।
→ ଅନୁସିଦ୍ଧାନ୍ତ 2 : P₁, P₂ ବିନ୍ଦୁଦ୍ଵୟ x-ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ହେଲେ P₁P₂ = | x₂ – x₁ | ଓ y-ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ହେଲେ, P₁P₂ = | y₂ – y₁ | ହେବ ।

→ ବିଭାଜନ ସୂତ୍ର (Division Formula) :
ସଂଜ୍ଞା : ଅନ୍ତର୍ବିଭାଜନ :
ଯଦି A-P-B ହୁଏ, ଅର୍ଥାତ୍ AB ଉପରେ A ଓ B ବିନ୍ଦୁଦ୍ଵୟର ମଧ୍ୟବର୍ତୀ P ବିନ୍ଦୁ ହୁଏ, ତେବେ AB ରେଖାଖଣ୍ଡ P ବିନ୍ଦୁରେ \(\overline{\mathrm{AP}}\) ଓ \(\overline{\mathrm{PB}}\) ରେଖାଖଣ୍ଡରେ ଅନ୍ତର୍ବିଭକ୍ତ ହୁଏ ।
ଏ କ୍ଷେତ୍ରରେ AP + PB = AB ହୁଏ ଓ ଅନ୍ତର୍ବିଭକ୍ତ ହୋଇଥିବା ଦୁଇ ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟର ଅନୁପାତ AP : PB ।
ଯଦି P ବିନ୍ଦୁ AB ରେଖାଖଣ୍ଡକୁ m : n ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରେ, ଆମେ ଲେଖୁବା ଯେ, \(\frac{PA}{PB}=\frac{m}{n}\) ।
କିନ୍ତୁ P ବିନ୍ଦୁ BA ରେଖାଖଣ୍ଡକୁ r : s ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କଲେ, ଆମେ ଲେଖୁବା ଯେ, \(\frac{PB}{PA}=\frac{r}{s}\) ।

ଉପପାଦ୍ୟ 2 :
A (x,, y) ଓ B(x,, y,) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ AB, ଯଦି P(x, y) ବିନ୍ଦୁଦ୍ୱାରା m : n ଅନୁପାତରେ ଅନ୍ତର୍ବିଭାଜିତ ହୁଏ, ତେବେ P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ \(\frac{{mx}_2+{nx_1}}{m+n}, \frac{{my}_2+{ny_1}}{m+n}\) ହେବ ।
ଦତ୍ତ : ସ୍ଥାନାଙ୍କ ସମତଳରେ AB ରେଖାଖଣ୍ଡ ଉପରିସ୍ଥ P ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରି \(\frac{AP}{BP}=\frac{m}{n}\) ।

ମନେକର A, B ଓ P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (x₁, y₁), (x₂, y₂) ଓ (x, y) ।
ପ୍ରାମାଣ୍ୟ : P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) = (\(\frac{{mx}_2+{nx_1}}{m+n}, \frac{{my}_2+{ny_1}}{m+n}\))

→ ଅଙ୍କନ : A, P ଓ Bରୁ x-ଅକ୍ଷପ୍ରତି ଯଥାକ୍ରମେ AC, PM ଏବଂ BD ଲମ୍ବ ଏବଂ AS ⊥ PM, PT ⊥ BD ଅଙ୍କନ କର ।
ପ୍ରମାଣ : A ASP ଏବଂ A PTB ତ୍ରିଭୁଜଦ୍ଵୟ ମଧ୍ଯରେ m∠PAS = m∠BPT = 90°
m∠PAS = m∠BPT (ଅନୁରୂପ)
∴ ∆ ASP ଓ ∆ PTB ଦ୍ଵୟ ସଦୃଶ, ଅର୍ଥାତ୍ ∆ ASP – ∆ PTB
ତେଣୁ \(\frac{\mathrm{AS}}{\mathrm{PT}}=\frac{\mathrm{PS}}{\mathrm{BT}}=\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{\mathrm{m}}{\mathrm{n}}\) ଅର୍ଥାତ୍ \(\frac{\mathrm{AS}}{\mathrm{PT}}=\frac{\mathrm{m}}{\mathrm{n}}\) ଏବଂ \(\frac{\mathrm{PS}}{\mathrm{BT}}=\frac{\mathrm{m}}{\mathrm{n}}\)
ମାତ୍ର AS = CM = x – x₁, PT = MD = x₂ – x
ଏବଂ PS = PM – SM = PM – AC = y – y₁
BT = BD – TD = TD – PM = y₂ – y
\(\frac{\mathrm{AS}}{\mathrm{PT}}=\frac{x-x_1}{x_2-x}=\frac{m}{n}\) ⇒ mx₂ – mx = nx – nx₁ ⇒ mx₂ + nx₁ = mx + nx
⇒ x (m + n) = mx₂ + nx₁, PX = \(\frac{mx_2+nx_1}{m+n}\)
ସେହିପରି, \(\frac{\mathrm{AS}}{\mathrm{PT}}=\frac{y-y_1}{y_2-y}=\frac{m}{n}\) ⇒ my₂ – my = ny – ny₁
⇒ my₂ + ny₁ = my + ny ⇒ y (m + n) = my₂ + ny₁ ⇒ y = \(\frac{my_2+ny_1}{m+n}\)

→ ତେଣୁ A(x₁, y₁) ଓ B(x₂, y₂) ବିନ୍ଦୁଦ୍ଵୟର ସଂଯୋଗକାରୀ ରେଖାଖଣ୍ଡ ABକୁ m : n ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥ‌ିବା ବିନ୍ଦୁ P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) = \(\frac{mx_2+nx_1}{m+n}, \frac{my_2+ny_1}{m+n}\) ଅଟେ ।

• ଯଦି A – B – P ହୁଏ, ଅର୍ଥାତ୍‌ \(\overrightarrow{AB}\) ଉପରିସ୍ଥ P ଏକ ବିନ୍ଦୁ ହୁଏ, ତେବେ \(\overline{\mathrm{AB}}\), P ବିନ୍ଦୁଦ୍ଵାରା AP ଓ BP ରେଖାଖଣ୍ଡରେ ବହିର୍ବିଭକ୍ତ ହୋଇଛି ବୋଲି କୁହାଯାଏ ।
  
• ଏଠାରେ ବହିର୍ବିଭାଜନର ଅନୁପାତ AP : BP ହେବ ଓ AP – PB = AB ହେବ ।
• \(\frac{AB}{BP}\) < 1 ହେଲେ P – A – B ଏବଂ \(\frac{AB}{BP}\) > 1 ହେଲେ A – B – P ହେବ ।
• A(x₁, y₁) ଓ B(x₂, y₂) ବିଦୁ୍ୟଦ୍ୱୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡ AB, ଯଦି P(x, y) ଦ୍ଵାରା m : n ଅନୁପାତରେ ବହିର୍ବିଭାଜିତ ହୁଏ, ତେବେ P(x, y) ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ \(\frac{mx_2-nx_1}{m-n}, \frac{my_2-ny_1}{m-n}\) ହେବ ।
• ଯଦି P ବିଦୁଟି \(\overline{\mathrm{AB}}\) ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁ ହୁଏ, ସେ କ୍ଷେତ୍ରରେ m = n ହୁଏ ଏବଂ ମଧ୍ୟବିନ୍ଦୁ Pର ସ୍ଥାନାଙ୍କ (x, y) = \(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\) ହୁଏ ।