Odisha State Board BSE Odisha 10th Class Maths Notes Geometry Chapter 2 ବୃତ୍ତ will enable students to study smartly.
BSE Odisha Class 10 Maths Notes Geometry Chapter 2 ବୃତ୍ତ
→ ମୌଳିକ ଧାରଣା (Basic Concepts) :
- ଗୋଟିଏ ସମତଳରେ ଅବସ୍ଥିତ କୌଣସି ଏକ ଦତ୍ତ ବିନ୍ଦୁଠାରୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦୂରତାରେ ଉକ୍ତ ସମତଳରେ ଅବସ୍ଥିତ ସମସ୍ତ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍କୁ ବୃତ୍ତ (Circle) କୁହାଯାଏ ।
- ନିର୍ଦ୍ଦିଷ୍ଟ ବିନ୍ଦୁଟିକୁ ବୃତ୍ତର କେନ୍ଦ୍ର କୁହାଯାଏ ।
- ବୃତ୍ତର ବ୍ୟାସାର୍ଷ କହିଲେ ଆମେ ବୃତ୍ତର କେନ୍ଦ୍ର ଓ ବୃତ୍ତ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁର ଦୂରତାକୁ ବୁଝିଥାଉ ।
- ବୃତ୍ତର ଏକ ବ୍ୟାସାର୍ଷ କହିଲେ ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ P ଓ କେନ୍ଦ୍ର O ର ସଂଯୋଜକ ରେଖାଖଣ୍ଡ ।
- ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଏକ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ଏବଂ ‘ଏକ ବ୍ୟାସାର୍ଦ୍ଧ’ ହେଉଛି ଏକ ରେଖାଖଣ୍ଡ ।
- ବୃତ୍ତରେ ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁର ସଂଯୋଜକ ରେଖାଖଣ୍ଡକୁ ବୃତ୍ତର ଏକ ଜ୍ୟା (chord) କୁହାଯାଏ ।
- ଯେଉଁ ଜ୍ୟାରେ ବୃତ୍ତର କେନ୍ଦ୍ର ଅବସ୍ଥିତ ସେହି ଜ୍ୟାକୁ ବୃତ୍ତର ଏକ ବ୍ୟାସ କହନ୍ତି ।
ଗୋଟିଏ ବୃତ୍ତରେ ଏକ ବ୍ୟାସ ହେଉଛି ଏହାର ଦୀର୍ଘତମ ଜ୍ୟା ।
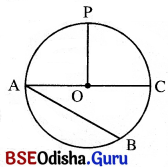
ଉପରିସ୍ଥ ବୃତ୍ତରେ O ବୃତ୍ତର କେନ୍ଦ୍ର ଏବଂ \(\overline{\mathrm{AB}}\) ବୃତ୍ତର ଏକ ଜ୍ୟା । \(\overline{\mathrm{AC}}\) ବୃତ୍ତର ବ୍ୟାସ ଏବଂ \(\overline{\mathrm{OP}}\) ବୃତ୍ତର ଏକ ବ୍ୟାସାର୍ଦ୍ଧ ।
ବୃତ୍ତର ଅନ୍ତର୍ଦେଶ ଓ ବହିର୍ଦେଶ (Interior and Exterior of Circle):
ବୃତ୍ତର କେନ୍ଦ୍ରଠାରୁ ଯେଉଁ ବିନ୍ଦୁମାନଙ୍କର ଦୂରତା ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧଠାରୁ କ୍ଷୁଦ୍ରତର, ସେଗୁଡ଼ିକୁ ବୃତ୍ତର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ (Interior points) କୁହାଯାଏ ଏବଂ ସମସ୍ତ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁମାନଙ୍କର ସମାହାରକୁ ବୃତ୍ତର ଅନ୍ତର୍ଦେଶ (Interior) କୁହାଯାଏ ।
(ii) ବୃତ୍ତ ଓ ଏହାର ଅନ୍ତର୍ଦେଶ ବ୍ୟତୀତ ସମତଳର ଅନ୍ୟ ସମସ୍ତ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍କୁ ବୃତ୍ତର୍ ବହିର୍ଦେଶ (Exterior) କୁହାଯାଏ । ବୃତ୍ତର ବହିର୍ଦେଶରେ ଥିବା ବିନ୍ଦୁମାନଙ୍କୁ ବୃତ୍ତର ବହିଃସ୍ଥ ବିନ୍ଦୁ କୁହାଯାଏ ।
ବୃତ୍ତର ଅନ୍ତର୍ଦେଶ ଏକ ଉତ୍ତଳ (convex) ସେଟ୍
- ସର୍ବସମ ବୃତ୍ତ : ଏକାଧିକ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ସମାନ ହେଲେ ସେମାନଙ୍କୁ ସର୍ବସମ ବୃତ୍ତ (Congruent circles) କୁହାଯାଏ ।
- ସର୍ବସମ କ୍ୟା : ଗୋଟିଏ ବୃତ୍ତରେ ବା ଏକାଧିକ ବୃତ୍ତରେ ଯେଉଁ ଜ୍ୟାମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ ସେମାନଙ୍କୁ ସର୍ବସମ ଜ୍ୟା (Congruent Chords) କୁହାଯାଏ ।
ଉପପାଦ୍ୟ 7 : ବୃତ୍ତର କେନ୍ଦ୍ରରୁ ଏହାର ବ୍ୟାସ ଭିନ୍ନ ଏକ ଜ୍ୟା ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ଉକ୍ତ ଜ୍ୟାକୁ ସମଦ୍ବିଖଣ୍ଡ କରେ ।
ଅନୁସିଦ୍ଧାନ୍ତ : ଗୋଟିଏ ସରଳରେଖା ବୃତ୍ତକୁ ଦୁଇଟିରୁ ଅଧିକ ବିନ୍ଦୁରେ ଛେଦ କରେ ନାହିଁ ।
ପ୍ରମେୟ 2.1 :
କୌଣସି ବୃତ୍ତର ବ୍ୟାସ ଭିନ୍ନ ଏକ ଜ୍ୟାର ମଧ୍ୟବିନ୍ଦୁ ଓ କେନ୍ଦ୍ରକୁ ଯୋଗକରୁଥିବା ରେଖା ଉକ୍ତ ଜ୍ୟା ଅଟେ ।
ଅନୁସିଦ୍ଧାନ୍ତ 1: ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର ଏହାର ଯେକୌଣସି ଜ୍ୟାର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ ଉପରେ ଅବସ୍ଥିତ । କାରଣ ଯେକୌଣସି ଜ୍ୟାର ମଧ୍ୟବିନ୍ଦୁଠାରେ କେବଳ ଗୋଟିଏ ମାତ୍ର ଲମ୍ବ ଅଙ୍କିତ ହୋଇପାରିବ ।
ଅନୁସିଦ୍ଧାନ୍ତ 2:
(i) ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ଅସମାନ୍ତର ଜ୍ୟାର ସମର୍ଦ୍ଦିଖଣ୍ଡକ ଲୟଦ୍ୱୟ ବୃତ୍ତର କେନ୍ଦ୍ରରେ ମିଳିତ ହୁଅନ୍ତି । କାରଣ ଅନୁସିଦ୍ଧାନ୍ତ-1 ଅନୁଯାୟୀ ବୃତ୍ତର କେନ୍ଦ୍ର ପ୍ରତ୍ୟେକ ସମଦ୍ୱିଖଣ୍ଡକ ଲମ୍ବ ଉପରେ ଅବସ୍ଥିତ ।
(ii) ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ସମାନ୍ତର ଜ୍ୟାର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବଦ୍ଵୟ ବୃତ୍ତର କେନ୍ଦ୍ର ଦେଇ ଯାଇଥିବା ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ।
କାରଣ ଏକ ଜ୍ୟାର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ସର୍ବଦା କେନ୍ଦ୍ରଦେଇ ଯିବ ଏବଂ ଜ୍ୟାଦ୍ଵୟ ସମାନ୍ତର ହେତୁ ଅନ୍ୟ ଜ୍ୟା ପ୍ରତି ଲମ୍ବ ହେବ ଏବଂ ବୃତ୍ତର କେନ୍ଦ୍ରରୁ ଏକ ଜ୍ୟା ପ୍ରତି ଗୋଟିଏ ମାତ୍ର ଲମ୍ବ ଅଙ୍କନ ସମ୍ଭବ ।
- \(\overline{\mathrm{AB}}\) ବୃତ୍ତର ଏକ ଜ୍ୟା ହେଲେ A ଓ B ଭିନ୍ନ ଜ୍ୟାଟିର ଅନ୍ୟ ସମସ୍ତ ବିନ୍ଦୁ ବୃତ୍ତର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
- ଯଦି A ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ଓ P ବୃତ୍ତର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ହୁଏ, ତେବେ \(\overrightarrow{\mathrm{AP}}\) ବୃତ୍ତକୁ ଅନ୍ୟ ଏକ ବିନ୍ଦୁରେ ଛେଦକରିବ ।
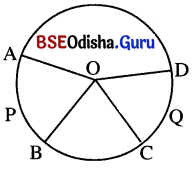
- ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବୃତ୍ତ ଅଙ୍କନ କରିବା ପାଇଁ ଅତି କମ୍ରେ ତିନୋଟି ବିନ୍ଦୁର ଅବସ୍ଥିତି ଜାଣିବା ଆବଶ୍ୟକ ।
![]()
ପ୍ରମେୟ 2.2 :
ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ନ ଥୁବା ଯେକୌଣସି ତିନୋଟି ବିନ୍ଦୁ ମଧ୍ୟ ଦେଇ ଗୋଟିଏ ଏବଂ କେବଳ ବୃତ୍ତ ଅଙ୍କନ କରାଯାଇ ପାରିବ ।
ତ୍ରିଭୁଜର ପରିବୃତ୍ତର ସଂଜ୍ଞା :
ଗୋଟିଏ ତ୍ରିଭୁଜର ଶୀର୍ଷବିଦୁ୍ୟତ୍ରୟ ଦେଇ ଅଙ୍କିତ ବୃତ୍ତକୁ ଉକ୍ତ ତ୍ରିଭୁଜର ପରିବୃତ୍ତ (Circum-Circle) ଓ ଏହାର କେନ୍ଦ୍ରବିନ୍ଦୁକୁ ଉକ୍ତ ତ୍ରିଭୁଜର ପରିକେନ୍ଦ୍ର (Circum-Centre) କୁହାଯାଏ ।
ଅନୁସିଦ୍ଧାନ୍ତ : ଦୁଇଟି ବୃତ୍ତ ପରସ୍ପରକୁ ଦୁଇଟିରୁ ଅଧ୍ଵ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ନାହିଁ ।
ଉପପାଦ୍ୟ 8 :
ଗୋଟିଏ ବୃତ୍ତର ସମାନ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ଜ୍ୟାମାନେ କେନ୍ଦ୍ରଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।
କଥନ : ଦୁଇଟି ସର୍ବସମ ବୃତ୍ତର ସମାନ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ଜ୍ୟାମାନେ ନିଜ ନିଜ କେନ୍ଦ୍ରଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।
ପ୍ରମେୟ 2.3 :
ଗୋଟିଏ ବୃତ୍ତରେ କେନ୍ଦ୍ରଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ଜ୍ୟାମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ ।
କଥନ : ଦୁଇଟି ସର୍ବସମ ବୃତ୍ତରେ ନିଜ ନିଜ କେନ୍ଦ୍ରଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ଜ୍ୟାମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 1: ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ଜ୍ୟା ମଧ୍ୟରେ କେନ୍ଦ୍ରଠାରୁ ଦୂରବର୍ତ୍ତୀ ଜ୍ୟାର ଦୈର୍ଘ୍ୟ ନିକଟତର ଜ୍ୟାର ଦୈର୍ଘ୍ୟଠାରୁ କ୍ଷୁଦ୍ରତର ।
ଅନୁସିଦ୍ଧାନ୍ତ 2: ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ଜ୍ୟା ମଧ୍ୟରୁ କ୍ଷୁଦ୍ରତର ଜ୍ୟାଟି କେନ୍ଦ୍ରଠାରୁ ଅଧିକ ଦୂରବର୍ତ୍ତୀ ।
![]()
→ ଜ୍ୟାଦ୍ଵାରା କେନ୍ଦ୍ରରେ ଉତ୍ପନ୍ନ କୋଣ (Angle subtended by the chord at the centre) :
ଗୋଟିଏ ବୃତ୍ତର \(\overline{\mathrm{AB}}\) ବ୍ୟାସଭିନ୍ନ ଏକ ଜ୍ୟା ଏବଂ O କେନ୍ଦ୍ରବିନ୍ଦୁ ହେଲେ ∠AOBକୁ ଜ୍ଯା \(\overline{\mathrm{AB}}\) ଦ୍ଵାରା କେନ୍ଦ୍ରଠାରେ ଉତ୍ପନ୍ନ କୋଣ ଅଥବା \(\overline{\mathrm{AB}}\) ଜ୍ୟା ସହ ସଂପୃକ୍ତ କେନ୍ଦ୍ରସ୍ଥ କୋଣ (Central angle) କୁହାଯାଏ ।
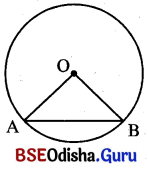
∠AOB, \(\overline{\mathrm{AB}}\) ଜ୍ୟା ସହ ସଂପୃକ୍ତ ଏକ କେନ୍ଦ୍ରସ୍ଥ କୌଣ ।
ଉପପାଦ୍ୟ 9 : ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ସର୍ବସମ ଜ୍ୟା କେନ୍ଦ୍ରଠାରେ ଯେଉଁ କୋଣ ଉତ୍ପନ୍ନ କରନ୍ତି ସେମାନେ ସର୍ବସମ ।
କଥନ : ଦୁଇଟି ସର୍ବସମ ବୃତ୍ତର ଦୁଇଟି ସର୍ବସମ ଜ୍ୟା ନିଜ ନିଜ କେନ୍ଦ୍ରଠାରେ ଯେଉଁ କୋଣ ଉତ୍ପନ୍ନ କରନ୍ତି ସର୍ବସମ ।
ପ୍ରମେୟ 2.4 :
ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ଜ୍ୟାଦ୍ଵାରା କେନ୍ଦ୍ରଠାରେ ଉତ୍ପନ୍ନ କୋଣ ଦୁଇଟି ସର୍ବସମ ହେଲେ ଜ୍ୟା ଦୁଇଟି ସର୍ବସମ ହେବେ ।
କଥନ : ଦୁଇଟି ସର୍ବସମ ବୃତ୍ତର ଦୁଇଟି ଜ୍ୟାଦ୍ଵାରା ନିଜ ନିଜ କେନ୍ଦ୍ରଠାରେ ଉତ୍ପନ୍ନ କୋଣ ଦୁଇଟି ସର୍ବସମ ହେଲେ ଜ୍ୟା ଦୁଇଟି ସର୍ବସମ ହେବେ ।
→ ଚାପ (Arc) :
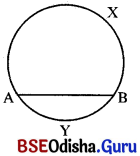
(i) ଚିତ୍ର (a)ରେ S ଏକ ବୃତ୍ତ ଏବଂ ଉକ୍ତ ବୃତ୍ତ ଉପରେ A ଓ B ଦୁଇଟି ଭିନ୍ନ ବିନ୍ଦୁ ହେଲେ ବୃତ୍ତଟି A ଓ B ବିନ୍ଦୁ ଦ୍ଵାରା ଦୁଇ ଭାଗରେ ବିଭକ୍ତ ହୁଏ । A ଓ B ବିନ୍ଦୁ ସମେତ ପ୍ରତ୍ୟେକ ଭାଗକୁ ଗୋଟିଏ ଗୋଟିଏ ଚାପ କୁହାଯାଏ ।
(ii) ଅନ୍ୟ ପ୍ରକାର କହିଲେ A ଓ B ବିନ୍ଦୁ ଦ୍ବୟ ସହିତ “A ଠାରୁ B ପର୍ଯ୍ୟନ୍ତ” ବୃତ୍ତର ଏକ ଅବିଛିନ୍ନ ଅଂଶ ହେଉଛି ଏକ ଚାପ । ଚିତ୍ର (b)ରେ \(\stackrel{\leftrightarrow}{AB}\), S ବୃତ୍ତର ଏକ ଛେଦକ (Secant) ।
(iii) P, ଛେଦକ \(\overleftrightarrow{AB}\) ର ଏକ ପାର୍ଶ୍ଵରେ ବୃତ୍ତ ଉପରିସ୍ଥ ଅନ୍ୟ ଏକ ବିନ୍ଦୁ ହେଉ । ବୃତ୍ତର ଯେଉଁ ଅଂଶରେ P ବିନ୍ଦୁ ଅଛି ସେହି ଅଂଶଟିକୁ APB ଅଥବା BPA ଚାପ କୁହାଯାଏ ।
ସଂକେତରେ ଚାପକୁ \(\widehat{\mathbf{A P B}}\) ବା \(\widehat{\mathbf{B P A}}\) ରୂପେ ଲେଖାଯାଏ ।
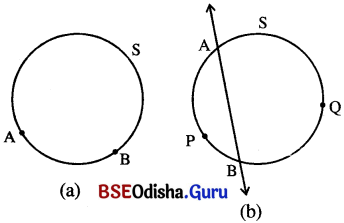
ସଂଜ୍ଞା : ଏକ ବୃତ୍ତ ଉପରିସ୍ଥ A ଓ B ଦୁଇଟି ବିନ୍ଦୁ ହେଲେ A ଓ B ବିନ୍ଦୁ ସମେତ \(\overline{\mathrm{AB}}\) କ୍ୟାର ଏକ ପାର୍ଶ୍ବରେ ଥିବା ବୃତ୍ତ ଉପରିସ୍ଥ ବିନ୍ଦୁମାନଙ୍କ ସେଟ୍କୁ ଏକ ଚାପ କୁହାଯାଏ । ଉକ୍ତ ସେଟ୍ ଅନ୍ତର୍ଭୁକ୍ତ P ଏକ ବିନ୍ଦୁ ହେଲେ ଉତ୍ପନ୍ନ ଚାପକୁ APB କିମ୍ବା BPA ଚାପରୂପେ ନାମିତ କରାଯାଏ ଏବଂ ଉକ୍ତ ଚାପକୁ \(\widehat{\mathbf{A P B}}\) କିମ୍ବା \(\widehat{\mathbf{B P A}}\) ସଂକେତ ଦ୍ବାରା ପ୍ରକାଶ କରାଯାଏ ।
(iv) \(\widehat{\mathbf{A P B}}\) ଏକ ଚାପ ହେଲେ A ଓ B, ଚାପର ଦୁଇଟି ପ୍ରାନ୍ତବିନ୍ଦୁ (End points) ଅଟନ୍ତି ଏବଂ ଚାପର ଅନ୍ୟ ସମସ୍ତ ବିନ୍ଦୁଙ୍କୁ ଚାପର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ (Interior points) କୁହାଯାଏ ।
(v) Q, ଛେଦକ \(\overleftrightarrow{AB}\) ର ଅପର ପାର୍ଶ୍ଵ ଚିତ୍ର (b)ରେ ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେଲେ AQB ଚାପକୁ \(\widehat{\mathbf{A Q B}}\) ବା BQÀ ସଂକେତ ଦ୍ଵାରା ପ୍ରକାଶ କରାଯାଏ ।
(vi) A ଓ B ଉଭୟ \(\widehat{\mathbf{A P B}}\) ଏବଂ \(\widehat{\mathbf{A Q B}}\) ଚାପର ପ୍ରାନ୍ତବିନ୍ଦୁ ଅଟନ୍ତି । \(\widehat{\mathbf{A P B}}\) ଓ \(\widehat{\mathbf{A Q B}}\) ଚାପଦ୍ଵୟକୁ ପରସ୍ପରର ବିପରୀତ ଚାପ (Opposite are) କୁହାଯାଏ । ଉକ୍ତ ଚାପଦ୍ଵୟର ସଂଯୋଗରେ ସମ୍ପୂର୍ଣ୍ଣ ବୃତ୍ତଟି ଗଠିତ ହେଉଥିବାରୁ ଗୋଟିକୁ ଅପରର ପରିପୂରକ ଚାପ (Supplementary are) ମଧ୍ୟ କୁହାଯାଏ । ଏହି ଚାପଦ୍ଵୟକୁ \(\overline{\mathrm{AB}}\) ଜ୍ୟା ଦ୍ବାରା ଉତ୍ପନ୍ନ ବା ଛେଦିତ ଚାପ କୁହାଯାଏ ଏବଂ \(\overline{\mathrm{AB}}\) ଜ୍ୟାକୁ ଉଭୟ ଚାପର ସମ୍ପୃକ୍ତ ଜ୍ୟା (Corresponding chord) କୁହାଯାଏ ।
→ କ୍ଷୁଦ୍ରଚାପ, ବୃହତ୍ପ ଏବଂ ଅଭିବୃତ୍ତ (Minor arc, Major arc and Semi circle) :
କ୍ଷୁଦ୍ରଚାପ, ବୃହତ୍ପ (Minor are, Major arc) :
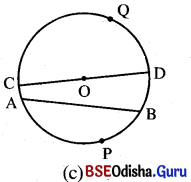
(i) ଯଦି କୌଣସି ଚାପ \(\widehat{\mathbf{A P B}}\)ର P ବିନ୍ଦୁ ଏବଂ ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ ସମ୍ପୃକ୍ତ \(\overline{\mathrm{AB}}\) ଜ୍ୟାର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ହୁଅନ୍ତି ତେବେ \(\widehat{\mathbf{A P B}}\)କୁ ଏକ କ୍ଷୁଦ୍ରଚାପ (Minor are) କୁହାଯାଏ । ଏକ କ୍ଷୁଦ୍ରଚାପର ବିପରୀତ ଚାପକୁ ବୃହତ୍ପ (Major acr) କୁହାଯାଏ ।
(ii) ଚିତ୍ର (c)ରେ \(\widehat{\mathbf{A P B}}\) କ୍ଷୁଦ୍ରଚାପ ଓ \(\widehat{\mathbf{A Q B}}\) ବୃହତ୍ ଚାପ ଅଟନ୍ତି । \(\widehat{\mathbf{A P B}}\) ଏକ କ୍ଷୁଦ୍ରଚାପ ହେଲେ ଏହାକୁ ‘AB କ୍ଷୁଦ୍ରଚାପ’ ଦ୍ଵାରା ପ୍ରକାଶ କରାଯାଏ ଓ ସେହିପରି \(\widehat{\mathbf{A Q B}}\) ବୃହତ୍ ଚାପକୁ ‘‘AB ବୃହତ୍ ଚାପ’’ ଦ୍ବାରା ପ୍ରକାଶ
କରାଯାଏ ।
→ ଅଦ୍ଧବୃତ୍ତ (Semi Circle) :
ଏକ ବୃତ୍ତରେ କୌଣସି ଚାପର ସମ୍ପୃକ୍ତ ଜ୍ୟା ବୃତ୍ତର ଏକ ବ୍ୟାସ ହେଲେ ଚାପଟିକୁ ଏକ ଅଦ୍ଧବୃତ୍ତ (Semi circle) କୁହାଯାଏ । ଚିତ୍ର (c)ରେ \(\widehat{\mathbf{C Q D}}\) ଏବଂ \(\widehat{\mathbf{C P D}}\) ପ୍ରତ୍ୟେକ ଅର୍ଦ୍ଧବୃତ୍ତ ଅଟନ୍ତି । ସଂଜ୍ଞାନୁସାରେ ଅର୍ଦ୍ଧବୃତ୍ତ ଏକ କ୍ଷୁଦ୍ରଚାପ ବା ବୃହତ୍ ଚାପ ନୁହେଁ । ଏକ ଅର୍ବବୃତ୍ତର ବିପରୀତ ଚାପ ମଧ୍ଯ ଏକ ଅଦ୍ଧବୃତ୍ତ ।
→ ଚାପର ଦୈର୍ଘ୍ୟ (Length of the arc):
\(\overline{\mathrm{AB}}\) ଜ୍ୟା ଦ୍ୱାରା ଉତ୍ପନ୍ନ ଚାପ ଦ୍ଵୟ ମଧ୍ୟରୁ କ୍ଷୁଦ୍ର ଚାପର ଦୈର୍ଘ୍ୟ ବୃହତ୍ ଚାପର ଦୈର୍ଘ୍ୟଠାରୁ କ୍ଷୁଦ୍ରତର । ଚାପର ଦୈର୍ଘ୍ୟ (length) କୁ l ଚିହ୍ନଦ୍ଵାରା ସୂଚିତ କରାଯାଏ । l \(\widehat{\mathbf{A P Q}}\), \(\widehat{\mathbf{A P Q}}\) ଚାପର ଦୈର୍ଘ୍ୟମାପକୁ ସୂଚାଏ । ଦୁଇ ବିପରୀତ ଚାପର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ବୃତ୍ତର ଦୈର୍ଘ୍ୟ ଅଟେ । ବୃତ୍ତର ଦୈର୍ଘ୍ୟକୁ ବୃତ୍ତର ପରିଧ (Circumference) କୁହାଯାଏ ।
→ ସନ୍ନିହିତ ଚାପ (Adjacent arcs) :
ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ଚାପର ଗୋଟିଏ ମାତ୍ର ସାଧାରଣ ବିନ୍ଦୁ ଥିଲେ ଉକ୍ତ ବିନ୍ଦୁଟି ପ୍ରତ୍ୟେକ ଚାପର ଏକ ପ୍ରାନ୍ତ ବିନ୍ଦୁ ହେବ ଏବଂ ଏହିପରି ଦୁଇଟି ଚାପକୁ ସନ୍ନିହିତ ଚାପ (Adjacent ares) କୁହାଯାଏ । ଦୁଇଟି ସନ୍ନିହିତ ଚାପର ସଂଯୋଗରେ ନୂତନ ଚାପ ଗଠିତ ହୁଏ । ଚିତ୍ରରେ \(\widehat{\mathbf{OCA}}\) ଏବଂ \(\widehat{\mathbf{APB}}\) ଦୁଇଟି ସନ୍ନିହିତ ଚାପର ସଂଯୋଗରେ \(\widehat{\mathbf{QAB}}\) ଗଠିତ ହେଉଅଛି ।
ମନେରଖ : ଦୁଇଟି ବୃହତ୍ ଚାପ କିମ୍ବା ଦୁଇଟି ଅଦ୍ଧବୃତ୍ତ ସନ୍ନିହିତ ଚାପ ହୋଇପାରିବ ନାହିଁ ।
→ ଚାପଦ୍ବାରା ଉତ୍ପନ୍ନ କୋଣ (Angle subtended by an Arc):
(i) ଗୋଟିଏ ବୃତ୍ତରେ \(\widehat{\mathbf{APB}}\) ଏକ କ୍ଷୁଦ୍ର ଚାପ । X, \(\overline{\mathrm{AB}}\) ଜ୍ୟା ଉପରେ ନ ଥିବା ବୃତ୍ତର ସମତଳରେ ଅନ୍ୟ ଏକ ବିନ୍ଦୁ ହେଲେ ∠AXBକୁ \(\widehat{\mathbf{APB}}\) ଚାପଦ୍ବାରା X ଠାରେ ଉତ୍ପନ୍ନ କୋଣ (angle subtended at X) କୁହାଯାଏ ।
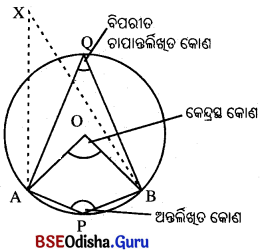
(ii) ବତ୍ତର କେନ୍ଦ୍ର ଠ ହେଲେ ∠AOB କୁ \(\widehat{\mathbf{APB}}\) ଦ୍ଵାରା କେନ୍ଦ୍ରଠାରେ ଉତ୍ପନ୍ନ କୋଣ ବା ସଂକ୍ଷେପରେ \(\widehat{\mathbf{APB}}\) ର କେନ୍ଦ୍ରସ୍ଥ କୋଣ (Central angle) କୁହାଯାଏ । ଅର୍ଥାତ୍ ଏକ କ୍ଷୁଦ୍ର ଚାପଦ୍ବାରା କେନ୍ଦ୍ରଠାରେ ଉତ୍ପନ୍ନ କୋଣ ଉକ୍ତ ଚାପର କେନ୍ଦ୍ରସ୍ଥ କୋଣ ।
(iii) \(\widehat{\mathbf{AB}}\) ର P ଯେକୌଣସି ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ହେଲେ ∠APB କୁ \(\widehat{\mathbf{AB}}\) ଚାପର ଏକ ଅନ୍ତର୍ଲିଖ କୋଣ (Inscribed angle) କୁହାଯାଏ । Q, \(\widehat{\mathbf{APB}}\) ର ବିପରୀତ ଚାପ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେଲେ ∠AQBକୁ \(\widehat{\mathbf{APB}}\) ଚାପର ବିପରୀତ ଚାପାନ୍ତର୍ଲିଖ୍ ବା ପରିପୂରକ ଚାପାନ୍ତର୍ଲିଖୁତ କୋଣ (Angle subtended at a point on the opposite arc or supplementary arc) କୁହାଯାଏ ।
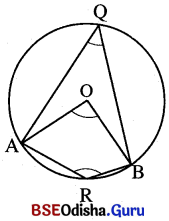
(iv) ∠AOB ଟି \(\overline{\mathrm{AB}}\) କ୍ୟା ଦ୍ବାରା ଉତ୍ପନ୍ନ କେନ୍ଦ୍ରସ୍ଥ କୋଣ । ଏହା ସ୍ପଷ୍ଟ ଯେ \(\overline{\mathrm{AB}}\) ଜ୍ୟାଦ୍ବାରା ଉତ୍ପନ୍ନ କେନ୍ଦ୍ରସ୍ଥ କୋଣ ଏବଂ \(\widehat{\mathbf{AB}}\) କ୍ଷୁଦ୍ରଚାପ ଦ୍ବାରା ଉତ୍ପନ୍ନ କେନ୍ଦ୍ରସ୍ଥ କୋଣ ଦ୍ଵୟ ଅଭିନ୍ନ । ଚିତ୍ରରେ \(\widehat{\mathbf{AQB}}\) ଏକ ବୃହତ୍ ଚାପ ।
(v) \(\widehat{\mathbf{ARB}}\) ଦ୍ବାରା Q ଠାରେ ଉତ୍ପନ୍ନ କୋଣ ∠AQB, \(\widehat{\mathbf{AQB}}\)ର ଏକ ଅନ୍ତର୍ଲିଖୁତ କୋଣ । ∠ARB, \(\widehat{\mathbf{AQB}}\)ର ଏକ ବିପରୀତ ଚାପାନ୍ତଲିଷ୍କୃତ କୋଣ ।
→ କୋଣଦ୍ୱାରା ଛେଦିତ ଚାପ (Arc intercepted by the angle) :
ଗୋଟିଏ କୋଣର ବାହୁଦ୍ୱୟ ଏକ ବୃତ୍ତକୁ ଛେଦକଲେ କୋଣର ଅନ୍ତର୍ଦେଶରେ ଥିବା ଚାପ, ଯାହାର ପ୍ରାନ୍ତବିଦୁଦ୍ଵୟ କୋଣର ଦୁଇବାହୁ ହୁଅନ୍ତି, ତାହାକୁ ଉକ୍ତ କୋଣଦ୍ୱାରା ଛେଦିତ ଚାପ କୁହାଯାଏ ।
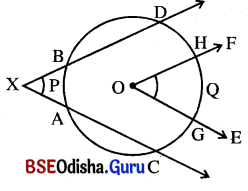
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ CEOF ଦ୍ୱାରା ଛେଦିତ ଚାପ \(\widehat{\mathbf{GQF}}\) ଏବଂ ∠AXB ଦ୍ୱାରା ଛେଦିତ ଚାପଦ୍ୱୟ \(\widehat{\mathbf{APB}}\) ଓ \(\widehat{\mathbf{CQD}}\) |
→ ଚାପର ଡିଗ୍ରୀ ପରିମାପ (Degree measure of an arc) :
ସଂଜ୍ଞା : କୌଣସି ଗୋଟିଏ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 0 ଓ 360° ମଧ୍ୟବର୍ତ୍ତୀ ଏକ ବାସ୍ତବ ସଂଖ୍ୟା ଯାହା ନିମ୍ନମତେ ସ୍ଥିରୀକୃତ ହୁଏ : ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରକୁ ଦେଖ ।
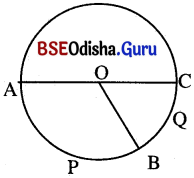
O ବୃତ୍ତର କେନ୍ଦ୍ର ହେଲେ,
(i) m\(\widehat{\mathbf{APB}}\) 818 = m∠AOB
(ii) m\(\widehat{\mathbf{ABC}}\) = 180°
(iii) m\(\widehat{\mathbf{ACB}}\) ବୃହତ୍ ଚାପ = 360°- m∠AOB
ସଂଜ୍ଞାନୁଯାୟୀ ଏକ ଚାପ ଓ ଏହାର ବିପରୀତ ଚାପର ଡିଗ୍ରୀ ପରିମାପର ସମଷ୍ଟି 360° ।
ବି.ଦ୍ର. m\(\widehat{\mathbf{APB}}\) ଦ୍ଵାରା \(\widehat{\mathbf{APB}}\)ର ଡିଗ୍ରୀ ପରିମାପକୁ ସୂଚିତ କରାଯାଏ ।
→ ଚାପର ସର୍ବସମତା (Congruence of arcs) :
ସଂଜ୍ଞା : ଗୋଟିଏ ବୃତ୍ତରେ (ଅଥବା ଦୁଇ ସର୍ବସମ ବୃତ୍ତରେ) ଦୁଇଟି ଚାପର ଡିଗ୍ରୀ ପରିମାପ ସମାନ ହେଲେ ଚାପ ଦୁଇଟି ସର୍ବସମ (Congruent) ହୁଅନ୍ତି ।
ଚିତ୍ରରେ m∠AOB = m∠COD ⇔ \(\widehat{\mathbf{APB}}\) ≅ \(\widehat{\mathbf{CQD}}\) |
ଏଥୁରୁ ସୁସ୍ପଷ୍ଟ ଯେ
(i) ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ସର୍ବସମ କ୍ଷୁଦ୍ରଚାପର କେନ୍ଦ୍ରସ୍ଥ କୌଣଦ୍ଵୟ ସର୍ବସମ ଏବଂ ବିପରୀତ କ୍ରମେ ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି କ୍ଷୁଦ୍ରଚାପର କେନ୍ଦ୍ରସ୍ଥ କୌଣଦ୍ଵୟ ସର୍ବସମ ହେଲେ କ୍ଷୁଦ୍ର ଚାପଦ୍ଵୟ ସର୍ବସମ ହେବେ ।
(ii) ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି କ୍ଷୁଦ୍ରଚାପ ସର୍ବସମ ହେଲେ ସେମାନଙ୍କର ବିପରୀତ ବୃହତ୍ ଚାପ ଦ୍ଵୟ ମଧ୍ୟ ସର୍ବସମ ହେବେ । ଏହାର ବିପରୀତ ଉକ୍ତିଟି ମଧ୍ୟ ସତ୍ୟ ।
(iii) ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ଅଦ୍ଧବୃତ୍ତ ସର୍ବସମ ।
ଗୋଟିଏ ବୃତ୍ତରେ ଚାପର ଦୈର୍ଘ୍ୟ ଚାପର କେନ୍ଦ୍ରସ୍ଥ କୌଣ ପରିମାପ ସହ ସମାନୁପାତୀ । କେନ୍ଦ୍ରସ୍ଥ କୌଣ ପରିମାଣର ହ୍ରାସ ବା ବୃଦ୍ଧି ସହିତ ଚାପର ଦୈର୍ଘ୍ୟର ସମାନୁପାତିକ ହ୍ରାସ ବା ବୃଦ୍ଧି ଘଟିଥାଏ ।
ମନେରଖ : ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ସର୍ବସମ ଚାପର ଦୈର୍ଘ୍ୟ ସମାନ ହୁଏ ଏବଂ ବିପରୀତ କ୍ରମେ ସମାନ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଚାପଦ୍ଵୟ ସର୍ବସମ ହୁଅନ୍ତି ।
ଉପପାଦ୍ୟ 10 : ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ସର୍ବସମ ଚାପ ସହ ସଂପୃକ୍ତ ଜ୍ୟାଦ୍ଵୟ ସର୍ବସମ ।
ମନ୍ତବ୍ୟ 1 : ଦୁଇଟି ସର୍ବସମ ବୃତ୍ତରେ ଦୁଇଟି ସର୍ବସମ ଚାପ ସହ ସଂପୃକ୍ତ ଜ୍ୟା ଦ୍ବୟ ସର୍ବସମ ।
ପ୍ରମେୟ 2.5 : କୌଣସି ବୃତ୍ତର ଦୁଇଟି ଜ୍ୟା ସର୍ବସମ ହେଲେ ସେମାନଙ୍କ ସହ ସଂପୃକ୍ତ (i) କ୍ଷୁଦ୍ରଚାପ ଦ୍ଵୟ ସର୍ବସମ ଏବଂ (ii) ବୃହତ୍ ଚାପଦ୍ଵୟ ସର୍ବସମ ।
→ ଗୋଟିଏ ଚାପର ଅନ୍ତର୍ଲିଖ୍ତ କୋଣ ସମ୍ପର୍କିତ ଏକ ଗୁରୁତ୍ଵପୂର୍ଣ ତଥ୍ୟ :
ପ୍ରମେୟ 2.6 : ଏକ ବୃତ୍ତରେ କୌଣସି ଚାପର ଅନ୍ତର୍ଲିଖ କୋଣର ପରିମାଣ ଏହାର ବିପରୀତ ଚାପର ଡିଗ୍ରୀ ପରିମାପର ଅର୍ଦ୍ଧେକ ।
ଅନୁସିଦ୍ଧାନ୍ତ 1 : (i) ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ସର୍ବସମ ଚାପର ଅନ୍ତର୍ଲିଖ କୋଣଦ୍ଵୟ ସର୍ବସମ । ବିପରୀତ କ୍ରମେ, ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ଚାପର ଅନ୍ତର୍ଲିଖତ କୋଣଦ୍ଵୟ ସର୍ବସମ ହେଲେ ଚାପଦ୍ଵୟ ସର୍ବସମ ।
(ii) ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ସର୍ବସମ ଚାପର ବିପରୀତ ଚାପାନ୍ତଲିଖ୍ତ କୋଣଦ୍ବୟ ସର୍ବସମ । ବିପରୀତ କ୍ରମେ ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ଚାପର ବିପରୀତ ଚାପାନ୍ତଲିଖ କୋଣଦ୍ୱୟ ସର୍ବସମ ହେଲେ ଚାପଦ୍ଵୟ ସର୍ବସମ ।
ଅନୁସିଦ୍ଧାନ୍ତ 2 : (i) ଗୋଟିଏ ବୃତ୍ତରେ କୌଣସି ଚାପର ଅନ୍ତର୍ଲିଖ କୋଣଗୁଡ଼ିକ ସର୍ବସମ ।
(ii) ଗୋଟିଏ ବୃତ୍ତରେ କୌଣସି ଚାପର ବିପରୀତ ଚାପାନ୍ତର୍ଲିଖ କୋଣଗୁଡ଼ିକ ସର୍ବସମ ।
ଅନୁସିଦ୍ଧାନ୍ତ 3 : ଏକ ଅଦ୍ଧବୃତ୍ତର ଅନ୍ତର୍ଲିଖ କୋଣ ସମକୋଣ ।
ଅନୁସିଦ୍ଧାନ୍ତ 4 : କୌଣସି ଚାପର ଅନ୍ତର୍ଲିଖ୍ କୋଣ ଏକ ସମକୋଣ ହେଲେ ଚାପଟି ଏକ ଅଦ୍ଧବୃତ୍ତ ।
→ ବୃତ୍ତଖଣ୍ଡ, ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ ଏବଂ ବୃତ୍ତକଳା (Segment, angle inscribed in a segment and sector) :
ବୃତ୍ତଖଣ୍ଡ (Segment) :
ବୃତ୍ତର ଏକ ଜ୍ୟା ଏବଂ ଜ୍ୟା ସହ ସଂପୃକ୍ତ କୌଣସି ଏକ ଚାପର ସଂଯୋଗରେ ଉତ୍ପନ୍ନ ସେଟ୍କୁ ଏକ ବୃତ୍ତଖଣ୍ଡ କୁହାଯାଏ ।
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AXBA ଏକ ବୃହତ୍ ବୃତ୍ତଖଣ୍ଡ (Major segment) ଓ AYB ଏକ କ୍ଷୁଦ୍ର ବୃତ୍ତଖଣ୍ଡ (Minor segment) ।
→ ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ (Angle inscribed in a segment) :
କୌଣସି ଚାପର ଏକ ଅନ୍ତର୍ଲିଖ କୋଣକୁ ସଂପୃକ୍ତ ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ କୁହାଯାଏ । ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ABXA ବୃତ୍ତଖଣ୍ଡସ୍ଥ ∠ADB ଗୋଟିଏ ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ ।
ସେହିପରି ∠ACB ମଧ୍ୟ ଗୋଟିଏ ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୌଣ ।
- କୌଣସି ଏକ ବୃତ୍ତଖଣ୍ଡସ୍ଥ ସମସ୍ତ କୋଣ ସର୍ବସମ ।
- ଅଦ୍ଧି ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ ଏକ ସମକୋଣ ।
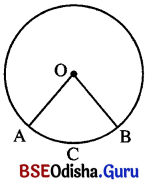
→ ବୃତ୍ତକଳା (Sector) :
ବୃତ୍ତର କୌଣସି ଏକ ଚାପ, ଚାପର ପ୍ରାନ୍ତବିନ୍ଦୁକୁ କେନ୍ଦ୍ର ସହିତ ଯୋଗ କରୁଥିବା ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ଵୟର ସଂଯୋଗରେ ବୃତ୍ତକଳା ଗଠିତ ହୁଏ । ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ OACB ଏକ ବୃତ୍ତକଳା ।
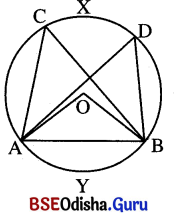
→ ବୃତ୍ତାନ୍ତର୍ଲିଖତ ଚତୁର୍ଭୁଜ (Cyclic quadrilateral) :
ସଂଜ୍ଞା : ଏକ ଚତୁର୍ଭୁଜର ଶୀର୍ଷବିଦୁଗୁଡ଼ିକ ଏକ ବୃତ୍ତ ଉପରେ ଅବସ୍ଥିତ ହେଉଥ୍ଲେ ଚତୁର୍ଭୁଜଟିକୁ ବୃତ୍ତାନ୍ତର୍ଲିଖତ ଚତୁର୍ଭୁଜ କୁହାଯାଏ ।
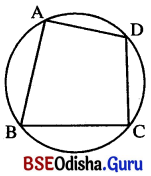
ପାର୍ଶ୍ୱ ସ୍ଥ ଚିତ୍ର ରେ ABCD ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖତ ଚତୁର୍ଭୁଜ ।
ପ୍ରମେୟ 2.7 :
ଦୁଇଟି ବିନ୍ଦୁର ସଂଯୋଜକ ରେଖାଖଣ୍ଡ ତା’ର ଏକ ପାର୍ଶ୍ଵରେ ଅନ୍ୟ ଦୁଇଟି ବିନ୍ଦୁଠାରେ ଉତ୍ପନ୍ନ କରୁଥିବା କୋଣଦ୍ଵୟ ସର୍ବସମ ହେଲେ ବିନ୍ଦୁ ଚାରିଟି ଏକ ବୃତ୍ତ ଉପରେ ରହିବେ ।
ଉପପାଦ୍ୟ 11 : ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ ଚତୁର୍ଭୁଜର ବିପରୀତ କୋଣମାନ ପରସ୍ପର ପରିପୂରକ ।
ମନ୍ତବ୍ୟ : ବୃତ୍ତାନ୍ତର୍ଲିଖତ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟ ପରସ୍ପରକୁ ଛେଦକରନ୍ତି ।
ଅନୁସିଦ୍ଧାନ୍ତ 1 : ବୃତ୍ତାନ୍ତର୍ଲିଖ ସାମାନ୍ତରିକ ଚିତ୍ର ଏକ ଆୟତଚିତ୍ର ।
ଅନୁସିଦ୍ଧାନ୍ତ 2 : ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ତ ରମ୍ବସ୍ ଏକ ବର୍ଗଚିତ୍ର ।
ଅନୁସିଦ୍ଧାନ୍ତ 3 : ବୃତ୍ତାନ୍ତଲିଵତ ଚତୁର୍ଭୁଜର ଏକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ଏହାର ଅନ୍ତଃସ୍ଥ ବିପରୀତ କୋଣର ପରିମାଣ ସହ ସମାନ ।
ପ୍ରମେୟ 2.8 : ଗୋଟିଏ ଚତୁର୍ଭୁଜର ବିପରୀତ କୌଣମାନ ପରସ୍ପର ପରିପୂରକ ହେଲେ ଚତୁର୍ଭୁଜଟି ବୃତ୍ତାନ୍ତର୍ଲିଖ ହେବ ।
