Odisha State Board BSE Odisha 10th Class Maths Notes Geometry Chapter 5 ପରିମିତି will enable students to study smartly.
BSE Odisha Class 10 Maths Notes Geometry Chapter 5 ପରିମିତି
→ ବୃତ୍ତର ପରିଧ୍ (Circumference of circle):
ବୃତ୍ତର ପରିସୀମାକୁ ବୃତ୍ତର ପରିସ୍ କୁହାଯାଏ ।
ବ୍ୟାସାର୍ଷକୁ ଯଥାକ୍ରମେ c, d ଓ r ଏକକ ରୂପେ ସୂଚିତ କରାଯାଏ ।
ବୃତ୍ତର ପରିସ୍ ଓ ବୃତ୍ତର ବ୍ୟାସର ଅନୁପାତ ସର୍ବଦା ଏକ ସ୍ଥିରାଙ୍କ । ଉକ୍ତ ସ୍ଥିରାଙ୍କ π ଯାହାକୁ Johann Lambert ଏକ ଅପରିମେୟ ସଂଖ୍ୟାର ଆଖ୍ୟା ଦେଇଥିଲେ ।
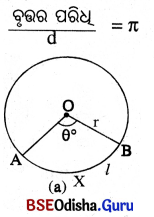
ବୃତ୍ତର ପରିସ୍ = πd, ଆମେ ଜାଣୁ d = 2r (r = ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ)
ବୃତ୍ତର ପରିଧ୍ (c) = π.2r = 2πr
![]()
→ ବୃତ୍ତର ଚାପର ଦୈର୍ଘ୍ୟ (Length of an arc)

ଅର୍ଥବୃତ୍ତର ପରିଧ୍ = πr
ଅର୍ଥବୃତ୍ତର ପରିସୀମା = πr + 2r
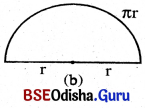
ଅର୍ଥବୃତ୍ତର ପରିସୀମା :
ଚିତ୍ର (a)ରେ OAXB ବୃତ୍ତକଳାର ପରିସୀମା = OA+OB+ \(\widehat{\mathbf{A X B}}\) ର ଦୈର୍ଘ୍ୟ
= 2OA + \(\widehat{\mathbf{A X B}}\)ର ଦୈର୍ଘ୍ୟ = (2r + l) ଏକକ ।
→ ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ (Area of a Circle) :
ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ A ଏବଂ ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ ଦ୍ବାରା ସୂଚିତ ହେଲେ
A = πr² ବର୍ଗ ଏକକ
![]()
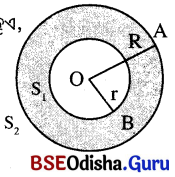
→ ବୃତ୍ତୀୟ ବଳୟର କ୍ଷେତ୍ରଫଳ (Area of a circular annulus) :
ବଳୟର କ୍ଷେତ୍ରଫଳ = ବାହାର ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ – ଭିତର ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ
ଯଦି ବହିଃବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ OA = R ଏକକ ଏବଂ ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ OB = r ଏକକ ହୁଏ,
ବୃତ୍ତୀୟ ବଳୟର କ୍ଷେତ୍ରଫଳ = π( R² – r²) ବର୍ଗ ଏକକ
→ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ (Area of a sectorial region) :
(i) ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ × ବ୍ୟାପଦ୍ଧ
ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) lr ବର୍ଗ ଏକକ
(ii) ବୃତ୍ତକଳାର ଚାପଟିର ଡିଗ୍ରୀ ପରିମାପ θ° ଏବଂ ବୃତ୍ତର ଡିଗ୍ରୀ ପରିମାପ 360° ହେଲେ ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ
ଦୁଇଟି ଏକକେନ୍ଦ୍ରୀକ ବୃତ୍ତକଳାଦ୍ୱୟର କ୍ଷେତ୍ରଫଳର ଅନ୍ତର = \(\frac{1}{2}\) × ବ୍ୟାସାର୍ଷଦ୍ୱୟର ଅନ୍ତର × ଚାପଦ୍ଵୟର
ସମଷ୍ଟି = \(\frac{1}{2}\) × ବ୍ୟାସାର୍ଷଦ୍ବୟର ସମଷ୍ଟି × ଚାପଦ୍ବୟର ଅନ୍ତର
ଯଦି ଏକକେନ୍ଦ୍ରୀକ ବୃତ୍ତକଳାଦ୍ୱୟର ବ୍ୟାସାର୍ଷଦ୍ବୟର R ଓ r ଏକକ ଏବଂ ଚାପଦ୍ଵୟ ଯଥାକ୍ରମେ L ଓ l ଏକକ ହୁଏ, ତେବେ
ବୃତ୍ତକଳାଦ୍ୱୟର କ୍ଷେତ୍ରଫଳର ଅନ୍ତର = \(\frac{1}{2}\) (R – r) (L + l) ବା \(\frac{1}{2}\) (R + r) (L – l)
![]()
→ ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ (Area of a sectorial region) :
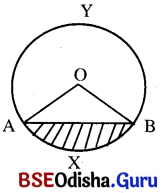
AXBA ବୃତ୍ତଖଣ୍ଡର କ୍ଷେତ୍ରଫଳ = OAXB ବୃତ୍ତକଳାର କ୍ଷେତ୍ରଫଳ – ∆ OAB ର କ୍ଷେତ୍ରଫଳ
ବୃହତ୍ ବୃତ୍ତଖଣ୍ଡ AYBAର କ୍ଷେତ୍ରଫଳ = ବୃତ୍ତର କ୍ଷେତ୍ରଫଳ – କ୍ଷୁଦ୍ର ବୃତ୍ତଖଣ୍ଡର AXBAର କ୍ଷେତ୍ରଫଳ ।
→ ପ୍ରିଜିମ୍ବର ପୃଷ୍ଟତଳର କ୍ଷେତ୍ରଫଳ (Surface Area of a Prism) :
ଏହା ଏକ ତ୍ରିଭୁଜାକାର ଆଧାର ବିଶିଷ୍ଟ ସରଳ ପ୍ରିଜିମ୍ ଯାହାର ଭୂମି ଓ ଶୀର୍ଷତଳଦ୍ଵୟ ତ୍ରିଭୁଜାକାର କ୍ଷେତ୍ର ଓ ପାର୍ଶ୍ଵତଳ ତ୍ରୟ ଆୟତକ୍ଷେତ୍ର ।
- ପ୍ରିଜିମ୍ର ପାର୍ଶ୍ଵତଳର କ୍ଷେତ୍ରଫଳ = ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା
- ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ପତଳର କ୍ଷେତ୍ରଫଳ = ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × ଆଧାରର କ୍ଷେତ୍ରଫଳ ।
→ ବୃତ୍ତଭୂମିକ ନିଦା ସରଳ ସିଲିଣ୍ଡର (ସମବର୍ଭୁଳ)ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (Curved surface area of a right circular solid cylinder):
ନିଦା ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ ଓ ଉଚ୍ଚତା h ଏକକ ହେଲେ
(i) ସିଲିଣ୍ଡରର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳ ବା ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ସିଲିଣ୍ଡରର ଆଧାରର ପରିଧ୍ × ଉଚ୍ଚତା
= 2лrh ବର୍ଗ ଏକକ
(ii) ସିଲିଣ୍ଡରର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = = ବକ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × ଆଧାରର କ୍ଷେତ୍ରଫଳ
= 2xrh + 2πr² = 2πr (h + r) ବର୍ଗ ଏକକ
→ ବୃତ୍ତୀୟ ବଳୟଭୂମିକ ଫମ୍ପା ସରଳ ସିଲିଣ୍ଡରର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (Surface area of a right circular cylinder) :
ଫମ୍ପା ସିଲିଣ୍ଡରର ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ, ବହିଃବ୍ୟାସାର୍ଦ୍ଧ R ଏକକ ଓ ଉଚ୍ଚତା h ଏକକ ହେଲେ
(i) ଫମ୍ପା ସିଲିଣ୍ଡରର ବହିଃପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πRh ବର୍ଗ ଏକକ
(ii) ଫମ୍ପା ସିଲିଣ୍ଡରର ଅନ୍ତଃପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πrh ବର୍ଗ ଏକକ
(iii) ଫମ୍ପା ସିଲିଣ୍ଡରର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πRh + 2πrh = 2π(R + r) h ବର୍ଗ ଏକକ
(iv) ଫମ୍ପା ସିଲିଣ୍ଡରର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = : ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × ଆଧାରର କ୍ଷେତ୍ରଫଳ
=2л(R + r) h + 2л(R² – r²) = 2л(R + r) [h+ (R – r)]
= 2л(R + r)(h + t) ବର୍ଗ ଏକକ [ବେଧ (t) = R – r]
