BSE Odisha 10th Class Maths Solutions Algebra Chapter 1 ସରଳ ସହସମୀକରଣ Ex 1(b)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 1 ସରଳ ସହସମୀକରଣ Ex 1(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 1 ସରଳ ସହସମୀକରଣ Ex 1(b)

Question 1.
ପ୍ରତିକଳ୍ପନ ପ୍ରଣାଳୀରେ ନିମ୍ନଲିଖ୍ ସହସମୀକରଣ ଦ୍ଵୟର ସମାଧାନ କର ।
(i) x + y – 8 = 0, 2x – 3y – 1 = 0
(ii) 3x + 2y – 5 = 0, x – 3y – 9 = 0
(iii) 2x – 5y + 8 = 0, x – 4y + 7 = 0
(iv) 11x + 15y + 23 = 0, 7x – 2y – 20 = 0
(v) ax + by – a + b = 0, bx – ay – a – b = 0
(vi) x + y – a = 0, ax + by – b² = 0
ସମାଧାନ ପ୍ରଣାଳୀ :
(i) ସହସମୀକରଣଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକରୁ ‘x’ କିମ୍ବା ‘y’ର ମାନ ନେଇ ଯଥାକ୍ରମେ y କିମ୍ବା x ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଏ ।
(ii) x କିମ୍ବା yର ମାନକୁ ଅନ୍ୟ ସମୀକରଣରେ ପ୍ରୟୋଗ କରି ଯଥାକ୍ରମେ y କିମ୍ବା x ର ମାନ ନିର୍ଣ୍ଣୟ କରାଯାଉ ।
(iii) ଉକ୍ତ ନିର୍ଣ୍ଣୟ ମାନକୁ (y କିମ୍ବା x) ନେଇ ଯେକୌଣସି ଗୋଟିଏ ସମୀକରଣରେ ପ୍ରୟୋଗ କରି ଅନ୍ୟଟିର ମାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
ସମାଧାନ :
(i) x + y – 8 = 0 …….(i) ଏବଂ
2x – 3y – 1 = 0 …….(ii)
ସମୀକରଣ (i)କୁ ବିଚାର କରି yକୁ x ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଉ ।
x + y – 8 = 0 ⇒ y = 8 – x ……..(iii)
y ର ମାନକୁ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ ପାଇବା 2x – 3(8 – x) – 1 = 0
⇒ 2x – 24 + 3x – 1 = 0 ⇒ 5x = 25 ⇒ x = \(\frac{25}{5}\) = 5
x ର ମାନ ସମୀକରଣ (iii)ରେ ପ୍ରୟୋଗ କଲେ, y = 8 – x = 8 – 5 = 3
∴ ନିର୍ଦେୟ ସମୀକରଣଦ୍ଵୟର ସମାଧାନ (x, y) = (5, 3) ଅଟେ ।

(ii) 3x + 2y – 5 = 0 …….(i) ଏବଂ
x – 3y – 9 = 0 …….(ii)
ସମୀକରଣ (i) ରୁ 3x = 5 – 2y ⇒ x = \(\frac{5-2y}{3}\) …….(iii)
‘x’ ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ, \(\frac{5-2y}{3}\) – 3y – 9 = 0
⇒ \(\frac{5-2y-9y-27}{3}\) ⇒ 0 = -22 – 11y = 0
⇒ 11y = -22 = y = \(\frac{-22}{11}\) = -2
yର ମାନ ସମୀକରଣ (iii)ରେ ପ୍ରୟୋଗ କଲେ,
x = \(\frac{5-2y}{3}\) = \(\frac{5-2(-2)}{3}\) = \(\frac{5+4}{3}\) = \(\frac{9}{3}=3\)
∴ ନିର୍ଦେୟ ସମୀକରଣଦ୍ଵୟର ସମାଧାନ (x, y) = (3, -2) ଅଟେ ।

(iii) 2x – 5y + 8 = 0 …….(i) ଏବଂ
x – 4y + 7 = 0 …….(ii)
ସମୀକରଣ (i) ରୁ ବିଚ।ର କରି x କୁ y ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଉ ।
2x – 5y + 8 = 0 ⇒ 2x = 5y – 8 ⇒ x = \(\frac{1}{2}\)(5y – 8) …….(iii)
‘x’ ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ, \(\frac{1}{2}\)(5y – 8) – 4y + 7 = 0
⇒ \(\frac{5y-8-8y+14}{2}\) = 0
⇒ -3y + 6 = 0 ⇒ y = \(\frac{-6}{-3}\) = 2
yର ମାନ ସମୀକରଣ (iii)ରେ ପ୍ରୟୋଗ କଲେ, x = \(\frac{1}{2}\)(5 × 2 – 8) = \(\frac{1}{2}\) × 2 = 1
∴ ନିର୍ଦେୟ ସମୀକରଣଦ୍ଵୟର ସମାଧାନ (x, y) = (1, 2) ଅଟେ ।

(iv) 11x + 15y + 23 = 0 …….(i) ଏବଂ
7x – 2y – 20 = 0 …….(ii)
ସମୀକରଣ (i) ରୁ ବିଚ।ର କରି y କୁ x ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଉ ।
11x + 15y + 23 = 0 ⇒ 15y = -11x – 23
⇒ y = \(\frac{1}{15}\)(-11x – 23) …….(iii)
‘y’ ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ, 7x – \(\frac{2}{15}\)(-11x – 23) = 20
⇒ \(\frac{105x+22x+46}{15}\) = 20
⇒ 127x = 300 – 46 ⇒ x = \(\frac{254}{127}\) = 2
x ର ମାନକୁ ସମୀକରଣ (iii) ରେ ପ୍ରୟୋଗ କଲେ, y = latex]\frac{1}{15}[/latex](-22 – 23) = \(\frac{1}{15}\) × -45 = -3
∴ ନିର୍ଦେୟ ସମାଧାନ (x, y) = (2, -3) ।

(v) ax + by – a + b = 0 …….(i) ଏବଂ
bx – ay – a – b = 0 …….(ii)
ସମୀକରଣ (i) ରୁ ବିଚ।ର କରି y କୁ x ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଉ ।
ax + by – a + b = 0 ⇒ by = -ax + a – b
⇒ y = \(\frac{1}{b}\)(-ax + a – b) …….(iii)
y ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ, bx – \(\frac{a}{b}\)(-ax + a – b) = 0
⇒ \(\frac{b^2x+a^2x-a^2 +ab-ab-b^2}{b}\) = 0
⇒ x(a² + b²) = a² + b² ⇒ x = \(\frac{a^2+b^2}{a^2+b^2}\) = 1
x ର ମାନକୁ ସମୀକରଣ (iii) ରେ ପ୍ରୟୋଗ କଲେ, y = latex]\frac{1}{b}[/latex](-a + a – b) ⇒ y = \(\frac{-b}{b}\) = -1
∴ ନିର୍ଦେୟ ସମାଧାନ (x, y) = (1, -1) ଅଟେ।

(vi) x + y – a = 0 …….(i) ଏବଂ
ax + by – b² = 0 …….(ii)
ସମୀକରଣ (i) ରୁ ବିଚ।ର କରି y କୁ x ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଉ ।
x + y – a = 0 ⇒ y = a – x …….(iii)
y ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ, ax + b(a – x) – b² = 0
⇒ ax + by – bx – b² = 0 ⇒ ax – bx = b² – ab
⇒ x(a – b) = -b(a – b) [a = b ତେଣୁ a – b ≠ 0]
ତେଣୁ x = -b
‘x’ ର ମାନକୁ ସମୀକରଣ (iii) ରେ ପ୍ରୟୋଗ କଲେ, y = a + b
∴ ନିର୍ଦେୟ ସମାଧାନ (x, y) = (-b, a+b)।

Question 2.
ଅପସାରଣ ପ୍ରଣାଳୀରେ ନିମ୍ନଲିଖ ସହ ସମୀକରଣମାନଙ୍କର ସମାଧାନ କର ।
(i) x – y – 3 = 0, 3x – 2y – 1 = 0
(ii) 3x + 4y = 10, 2x – 2y = 2
(iii) 3x – 5y – 4 = 0, 9x = 2y – 1
(iv) 0.4x – 1.5y = 6.5, 0.3x + 0.2y = 0.9
(v) √2x + √3y = 0, √5x + √2y = 0
(vi) ax + by = 0, x + y – c = 0 (a+b ≠ 0)
ସମାଧାନ ପ୍ରଣାଳୀ :
(i) ସମୀକରଣଦ୍ବୟରୁ ‘x’ ଅପସାରଣ କରାଯାଇ y ର ମାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
(ii) y ର ମାନକୁ ଯେକୌଣସି ସମୀକରଣରେ ପ୍ରୟୋଗ କରି x ର ମାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
(iii) ସେହିପରି ସମୀକରଣଦ୍ଵୟରୁ yକୁ ଅପସାରଣ କରାଯାଇ ‘x’ର ମାନ ନିର୍ଣ୍ଣୟ କରି ଏହାକୁ ଯେକୌଣସି ସମୀକରଣରେ ପ୍ରୟୋଗ କରି ‘y’ର ମାନ ନିର୍ଣ୍ଣୟ କରାଯାଇ ପାରିବ ।
ସମାଧାନ :
(i) x – y – 3 = 0 ……… (i) ଏବଂ
3x – 2y – 1 = 0 ………. (ii)

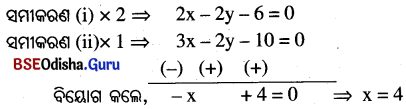
x ର ମାନକୁ ସମୀକରଣ (iii) ରେ ପ୍ରୟୋଗ କଲେ,
x – y – 3 = 0 ⇒ 4 – y – 3 = 0 ⇒ -y + 1 = 0 ⇒ y = 1
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (4, 1) ଅଟେ।

(ii) 3x + 4y = 10 ……… (i) ଏବଂ
2x – 2y = 2 ………. (ii)

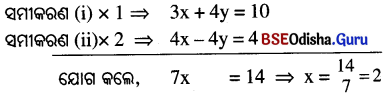
x ର ମାନକୁ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ,
3x + 4y = 10 ⇒ 2 + 4y = 10 ⇒ 4y = 10 – 6 ⇒ y = \(\frac{4}{4}\) = 1
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (2, 1) ଅଟେ।

(iii) 3x – 5y – 4 = 0 ……… (i) ଓ
9x = 2y – 1 ⇒ 9x – 2y + 1 = 0 ………. (ii)

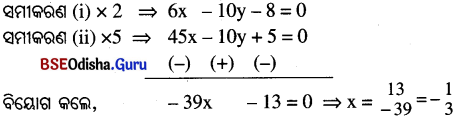
x ର ମାନକୁ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ,
3x – 5y – 4 = 0
⇒ 3 × (\(– \frac{1}{3}\)) – 5y – 4 = 0
⇒ -5y – 5 = 0 ⇒ y = \(\frac{5}{-5}\) = -1
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (\(– \frac{1}{3}\), -1) ଅଟେ।

(iv) 0.4x – 1.5y = 6.5 ……… (i) ଓ
0.3x + 0.2y = 0.9 ………. (ii)

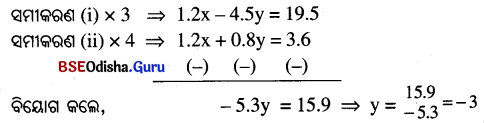
y ର ମାନକୁ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ,
0.4x – 1.5y = 6.5 ⇒ 0.4x + 4.5 = 6.5
⇒ 0.4x = 6.5 – 4.5 ⇒ 1.4x = 2 ⇒ x = \(\frac{2}{0.4}\) = 5
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (5, -3) ଅଟେ।

(v) √2x + √3y = 0 ……… (i) ଓ
√5x + √2y = 0 ………. (ii)

c₁ = c₂ = 0 ଓ a₁b₂ – a₂b₁ = 0 ହେଲେ ସମୀକରଣଦ୍ଵୟର ସମାଧାନଟି (0, 0) ଅଟେ ।
ଏଠାରେ c₁ = c₂ = 0 ଏବଂ \(\frac{\sqrt{2}}{\sqrt{5}} \neq \frac{\sqrt{3}}{\sqrt{2}}\)
ତେଣୁ ସହସମୀକରଣ ଦ୍ଵୟର ସମାଧାନ (0, 0) ଅଟେ ।
ବିକଳ୍ପ ପ୍ରଣାଳୀ :

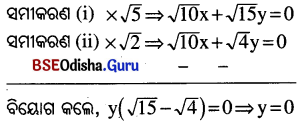
‘y’ ର ମାନକୁ ସମୀକରଣ (i)ରେ ପ୍ରୟୋଗ କଲେ,
√2x + √3 × 0 = 0 ⇒ √2x = 0 ⇒ x = 0
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (0, 0) ଅଟେ।

(v) ax + by = 0 ……… (i) ଏବଂ
x + y – c = 0 ………. (ii)

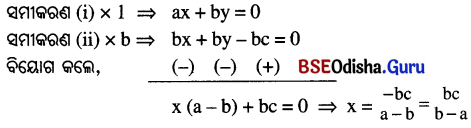
‘x’ ର ମାନକୁ ସମୀକରଣ (ii)ରେ ପ୍ରୟୋଗ କଲେ, y = c – x = c – \(\frac{bc}{b-a}\) =
= \(\frac{bc-ca-bc}{b-a}\) = \(\frac{-ca}{b-a}\) = \(\frac{ca}{a-b}\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (\(\frac{bc}{b-a}\), \(\frac{ca}{a-b}\)) ଅଟେ।

Question 3.
ବଜ୍ରଗୁଣନ ପ୍ରଣାଳୀରେ ନିମ୍ନଲିଖୂତ ସହ ସମୀକରଣମାନଙ୍କର ସମାଧାନ କର ।
(1) x + 2y + 1 = 0, 2x – 3y – 12 = 0
(ii) 2x + 5y = 1, 2x + 3y = 3
(iii) x + 6y + 1 = 0, 2x + 3y + 8 = 0
(iv) \(\frac{x}{a}+\frac{y}{b}\) = a+b, \(\frac{x}{a^2}+\frac{y}{b^2}\) = 2
(v) x + 6y + 1 = 0, 2x + 3y + 8 = 0
(vi) 4x – 9y = 0, 3x + 2y – 35 = 0
ବଜ୍ରଗୁଣନ ପୃତ୍ର : \(\frac{x}{b_1c_2-b_2c_1}=\frac{y}{c_1a_2-c_2a_1}=\frac{x}{a_1b_2-a_2b_1}\)
ଯେଉଁଠାରେ a₁b₂ = a₂b₁ ≠ 0
ସମାଧାନ :
(i) x + 2y + 1 = 0 ……… (i) ଏବଂ
2x – 3y – 12 = 0 ………. (ii)
ସମୀକରଣମାନଙ୍କର a₁b₂ – a₂b₁ = (1)(-3) – (2)(2) = -7 ≠ 0
ତେଣୁ ସମାଧାନ ସମ୍ଭବ।
ବଜ୍ରଗୁଣନ ପ୍ରଣାଳୀ ଅବଲମୂନରେ।

⇒ \(\frac{x}{-21}=\frac{y}{14}=\frac{1}{-7}\)
⇒ x = \(\frac{-21}{-7}\) ଓ y = \(\frac{14}{-7}\)
⇒ x = 3 ଓ y = -2
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (3, -2) ଅଟେ।

(ii) 2x + 5y = 1 ……… (i) ଏବଂ
2x + 3y = 3 ………. (ii)
ସମୀକରଣ (i) ଓ (ii) ଦ୍ବୟରୁ 2x + 5y = 1, 2x + 3y = 3
ସମୀକରଣମାନଙ୍କର a₁b₂ – a₂b₁ = (2)(3) – (2)(5) = -4 ≠ 0
ତେଣୁ ସହସମୀକରଣ ଦ୍ଵୟର ସମାଧାନ ସମ୍ଭବ ।
ବଜ୍ରଗୁଣନ ପ୍ରଣାଳୀ ଅବଲମୂନରେ।

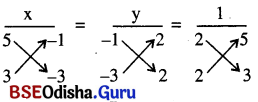
⇒ \(\frac{x}{15-(-3)}=\frac{y}{-2-(-6)}=\frac{1}{6-10}\)
⇒ \(\frac{x}{15+3}=\frac{y}{-2+6}=\frac{1}{6-10}\)
⇒ \(\frac{x}{-12}=\frac{y}{4}=\frac{1}{-4}\)
⇒ x = \(\frac{-12}{-4}=3\) ଓ y = \(\frac{4}{-4}=-1\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (3, -2) ଅଟେ।

(iii) x + 6y + 1 = 0 ……… (i) ଏବଂ
2x + 3y + 8 = 0 ………. (ii)
ଏଠାରେ a₁b₂ – a₂b₁ = (1)(3) – (2)(6) = 3- 12 = -9 ≠ 0
ତେଣୁ ଦତ୍ତ ସହସମୀକରଣ ଦ୍ଵୟର ସମାଧାନ ସମ୍ଭବ ।
ବଜ୍ରଗୁଣନ ପ୍ରଣାଳୀ ଅବଲମୂନରେ

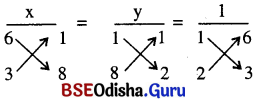
⇒ \(\frac{x}{48-3}=\frac{y}{2-86}=\frac{1}{3-12}\)
⇒ \(\frac{x}{45}=\frac{y}{-6}=\frac{1}{-9}\)
⇒ x = \(\frac{-45}{-9}=-5\) ଓ y = \(\frac{-6}{-9}=\frac{2}{3}\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (-5, \(\frac{2}{3}\)) ଅଟେ।

(iv) \(\frac{x}{a}+\frac{y}{b}\) = a+b ……… (i)
\(\frac{x}{a^2}+\frac{y}{b^2}=2\) ………. (ii)
ସମୀକରଣ (i) ଓ (ii) ରୁ \(\frac{x}{a}+\frac{y}{b}-(a+b)=0\), \(\frac{x}{a^2}+\frac{y}{b^2}-2=0\)

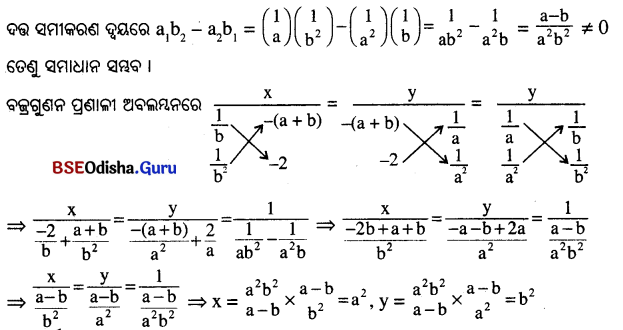
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (a², b²) ଅଟେ।

(v) x + 6y + 1 = 0 ……… (i)
2x + 3y + 8 = 0 ………. (ii)
ଏଠାରେ a₁ = 1
b₁ = 6
c₁ = 1
a₂ = 5
b₂ = 3
c₂ = 8
ପୁନଶ୍ଚ \({a_1}{a_2}=\frac{1}{2}\), \({b_1}{b_2}=\frac{6}{3}=2\)
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\), ତେଣୁ ସହ-ସମୀକରଣଦ୍ୱୟର ଅନନ୍ୟ ସମାଧାନ ରହିବ ।
b₁c₂ – b₂c₁ = 6 × 8 – 3 × 1 = 48 – 3 = 45
c₁a₂ – c₂a₁ = 1 × 2 – 8 × 1 = 2 – 8 = -6
a₁b₂ – a₂b₁ = 1 × 3 – 2 × 6 = 3 – 12 = -9

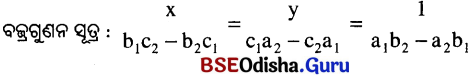
⇒ \(\frac{x}{45}=\frac{y}{-6}=\frac{1}{-9}\)
⇒ x = \(\frac{-45}{-9}=-5\) ଓ y = \(\frac{-6}{-9}=\frac{2}{3}\)
∴ ସମାଧାନ (x, y) = (-5, \(\frac{2}{3}\) ) ।

(vi) 4x – 9y = 0 ……… (i)
3x + 2y – 35 = 0 ………. (ii)
ଏଠାରେ a₁ = 4
b₁ = -9
c₁ = 0
a₂ = 3
b₂ = 2
c₂ = -35
ତେଣୁ ସହ-ସମୀକରଣଦ୍ୱୟର ଅନନ୍ୟ ସମାଧାନ ରହିବ ; \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) (\(\frac{4}{3} \neq \frac{-9}{2}\))
b₁c₂ – b₂c₁ = (-9)(-35) – 2 × 0 = 315
c₁a₂ – c₂a₁ = 0 × 3 – (-35) × 4 = 140
a₁b₂ – a₂b₁ = 4 × 2 – 3 × (-9) = 35 ≠ 0

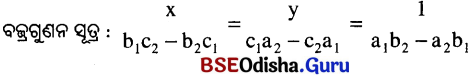
⇒ \(\frac{x}{315}=\frac{y}{140}=\frac{1}{35}\)
⇒ \(\frac{x}{9}=\frac{y}{4}=1\) ⇒ x = 9 ଓ y = 4
∴ ସମାଧାନ (x, y) = (9, 4) ।

Question 4.
ନିମ୍ନଲିଖ୍ ସହସମୀକରଣମାନଙ୍କ ସମାଧାନ କର ।
(i) \(\frac{2}{x}+\frac{3}{y}=17, \frac{1}{x}+\frac{1}{y}=7(x \neq 0, y \neq 0)\)
(ii) \(\frac{5}{x}+6 y=13, \frac{3}{x}+20 y=35(x \neq 0)\)
(iii) \(2 x-\frac{3}{y}=9,3 x+\frac{7}{y}=2(y \neq 0)\)
(iv) 4x + 6y = 3xy, 8x + 9y = 5xy (x ≠ 0, y ≠ 0)
(v) (a – b)x + (a + b)y = a² – 2ab – b², (a + b)x+(a + b)y = a² + b²
(vi) \(\frac{2}{x}+\frac{3}{y}=2\), ax – by = a² – b²
(vii) \(\frac{5}{x+y}-\frac{2}{x-y}+1=0, \frac{15}{x+y}+\frac{7}{x-y}-10=0\)
(viii) \(\frac{xy}{x+y}=\frac{6}{5}, \frac{xy}{x+y}=6(x+y \neq 0, x-y \neq 0)\)
(ix) 6x + 5y = 7, x + 3y + 1 = 2 (x + 6y – 1)
(x) \(\frac{x+y-8}{2}=\frac{x+2 y-14}{3}=\frac{3 x+y-12}{11}\)
(xi) \(\frac{x+y}{2}-\frac{x-y}{3}=8, \frac{x+y}{3}+\frac{x-y}{4}=11\)
(xii) \(\frac{x}{a}=\frac{y}{b}, ax + by=a^2+b^2 \)
ସମାଧାନ :
(i) \(\frac{2}{x}+\frac{3}{y}=17\) ⇒ \(\frac{2}{x}+\frac{3}{y}-17=0\) …….(1)
\(\frac{1}{x}+\frac{1}{y}=7\) ⇒ \(\frac{1}{x}+\frac{1}{y}-7=0\) …….(2)
ଏଠାରେ \(\frac{1}{x}=u\) ଏବଂ \(\frac{1}{x}=v\) ନେଲେ ଦତ୍ତ ସମୀକରଣଦ୍ବୟ
2u + 3v – 17 = 0, ଏବଂ u + v – 7 = 0 ହେବ ।
ଏଠାରେ a₁ = 2
b₁ = 3
c₁ = -17
a₂ = 1
b₂ = 1
c₂ = -7
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) ହୋଇଥିବାରୁ ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ରହିବ ।
b₁c₂ – b₂c₁ = (3)(-7) – 1(-17) = -21 – 17 = -4
c₁a₂ – c₂a₁ = (-17) × 1 – (-7) × 2 = -17 + 14 = -3
a₁b₂ – a₂b₁ = 2 × 1 – 1 × 3 = 2 – 3 = -1 (≠ 0)

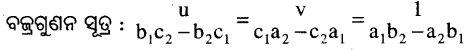
⇒ \(\frac{u}{-4}=\frac{v}{-3}=\frac{1}{-1}\) ⇒ u = 4 ଏବଂ v = 3
⇒ \(\frac{1}{x}=4\) ଏବଂ \(\frac{1}{y}=3\) ⇒ x = \(\frac{1}{4}\) ଏବଂ y = \(\frac{1}{3}\)
∴ ସମାଧାନ (x, y) = (\(\frac{1}{4}\), \(\frac{1}{3}\)) ।

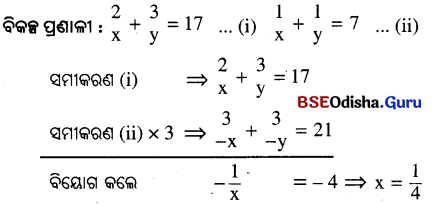
‘x’ ର ମାନ ସମୀକରଣରେ (ii) ପ୍ରୟୋଗ କଲେ y = \(\frac{1}{3}\) ହେବ ।

(ii) \(\frac{5}{x}+6 y=13\) ⇒ \(\frac{5}{x}+6 y-13=0\) ……..(1)
\(\frac{3}{x}+20 y=35\) ⇒ \(\frac{3}{x}+20 y-35=0\) ……….(2)

ସମୀକରଣ (1) ରେ x = \(\frac{41}{25}\)

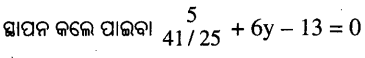
⇒ \(\frac{125}{41}+6 y-13=0 \Rightarrow 6 y=13-\frac{125}{41}=\frac{533-125}{41}\)
⇒ \(6 y=\frac{408}{41} \Rightarrow y=\frac{408}{41} \times \frac{1}{6}=\frac{68}{41}\)
∴ ସମାଧାନ (x, y) = (\(\frac{41}{25}\), \(\frac{68}{41}\)) ।

(iii) \(2 x-\frac{3}{y}=9,\) …….(i)
\(3 x+\frac{7}{y}=2\) …….(ii)

‘x’ ର ମାନ ସମୀକରଣରେ (ii) ପ୍ରୟୋଗ କଲେ 2 × 3 – \(\frac{3}{y}\) = 9 ⇒ – \(\frac{3}{y}\) = 9 – 6
⇒ 3y = -3 ⇒ y = -1
∴ ସମାଧାନ (x, y) = (3, -1)।

(iv) 4x + 6y = 3xy ………..(i)
8x + 9y = 5xy ………. (ii)
ସମୀକରଣ (i) ଓ (ii) ର ଉଭୟ ପାର୍ଶ୍ଵକୁ xy ଦ୍ବାରା ଭାଗକଲେ,
\(\frac{4}{y}+\frac{6}{x}=3\) …..(iii)
\(\frac{8}{y}+\frac{9}{x}=5\)
ମନେକର \(\frac{1}{x}=u\) ଓ \(\frac{1}{y}=v\)। ତେଣୁ ସମୀକରଣ (iii) ଓ (iv) ରୁ
6u + 4v = 3 ……(v), 9u + 8v = 5 ……..(vi)

ସମୀକରଣ (v) ରେ u = \(\frac{1}{3}\) ବସୀକଲେ, 6 × \(\frac{1}{3}\) + 4v = 3 ⇒ 4v = 1 ⇒ v = \(\frac{1}{4}\)
u = \(\frac{1}{3}\) ⇒ \(\frac{1}{x}\) = \(\frac{1}{3}\) ⇒ x = 3, v = \(\frac{1}{4}\) ⇒ \(\frac{1}{y}\) = \(\frac{1}{4}\) ⇒ y = 4
∴ ସମାଧାନ (x, y) = (3, 4)।

(v) (a – b)x + (a + b)y = a² – 2ab – b² ……..(i)
(a + b)x+(a + b)y = a² + b² ……….(ii)
ସମୀକରଣ (ii) କୁ ସମୀକରଣ (i) ରୁ ବିପ୍ରୟୋଗ କଲେ,
x(a + b) – x(a + b) = -2ab – 2b²
⇒ x(a + b – a – b) = -2ab – 2b²
⇒ -2bx = -2b(a + b) ⇒ x = a + b
‘x’ ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ, (a+b)(a+b) + (a+b) y = a² + b²
⇒ a² + b² + 2ab + (a + b) y = a² + b²
⇒ (a + b) y = -2ab ⇒ y = \(\frac{-2ab}{a+b}\)
∴ ସମାଧାନ (x, y) = (a+b, \(\frac{-2ab}{a+b}\))।

(vi) \(\frac{2}{x}+\frac{3}{y}=2\) ⇒ \(\frac{bx+ay}{ab}=2\)
⇒ bx + ay = 2ab ……(1), ax – by = a² – b² ………(2)

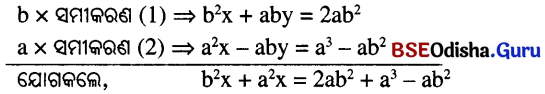
⇒ x(a² + b²) = a³ + ab² ⇒ x(a² + b²) = a(a² + b²) ⇒ x = a
ସମୀକରଣ (1) ରେ x = a ସ୍ଥାପନ କଲେ, b.a + ay = 2ab ⇒ ay = ab
⇒ y = b
∴ ସମାଧାନ (x, y) = (a, b)।

(vii) \(\frac{5}{x+y}-\frac{2}{x-y}+1=0\) ……..(i) ଏବଂ
\(\frac{15}{x+y}+\frac{7}{x-y}-10=0\) ……..(ii)
\(\frac{1}{x+y}=a\) ଏବଂ \(\frac{1}{x-y}=b\) ହେଲେ
ସମୀକରଣଦ୍ଵୟ 5a – 2b + 1 = 0 ………(iii) ଏବଂ 15a + 7b – 10 = 0 ……….(iv)

⇒ x – y = 1 …….. (v)
b ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗକଲେ,
5a – 2 × 1 + 1 = 0
⇒ 5a – 1 = 0 ⇒ 5a = 1 ⇒ a = \(\frac{1}{5}\)
⇒ \(\frac{1}{x+y}=\frac{1}{5}\) ⇒ x + y = 5 ……..(iv)
ସମୀକରଣ (v) ଓ (vi) ରୁ ୟୋଗକଲେ x + y + x – y = 5 + 1
⇒ 2x = 6 ⇒ x = 3
∴ ନିଶ୍ଚେୟ ସମାଧାନ (x, y) = (3, 2)।

(viii) \(\frac{xy}{x+y}=\frac{6}{5}\) …….(i)
\(\frac{xy}{x+y}=6\) ……..(ii)

⇒ \(\frac{1}{y}=\frac{2}{6}\) ⇒ \(\frac{1}{y}=\frac{1}{3}\) ⇒ y = 3
∴ ସମାଧାନ (x, y) = (2, 3)।

(ix) 6x + 5y = 7x + 3y + 1 = 2 (x + 6y – 1)
⇒ 6x + 5y = 7x + 3y + 1 ⇒ x – 2y + 1 = 0 ……(i)
ପୁନଶୃ 7x + 3y + 1 = 2 (x + 6y – 1)
⇒ 7x + 3y + 1 = 2x + 12y – 2 ⇒ 5x – 9y + 3 = 0 …..(ii)

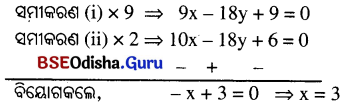
ସମୀକରଣ (i) ରେ x = 3 ସ୍ଥାପନ କଲେ, 3 – 2y + 1 = 0
⇒ 2y = 4 ⇒ y = 2
∴ ସମାଧାନ ପେଟ୍ (x, y) = (3, 2)।

(x) \(\frac{x+y-8}{2}=\frac{x+2 y-14}{3}=\frac{3 x+y-12}{11}\)
⇒ \(\frac{x+y-8}{2}=\frac{x+2 y-14}{3}\) ⇒ 3(x + y – 8) = 2(x + 2y – 14)
⇒ 3x + 3y – 24 = 2x + 4y – 28 ⇒ x – y = -4 ……..(i)
ପୁନଶୃ \(\frac{x+2 y-14}{3}=\frac{3 x+y-12}{11}\) ⇒ 11(x + 2y – 14) = 3(3x + y – 12)
⇒ 11x + 22y – 154 = 9x + 3y – 36 ⇒ 2x + 19y = 118 ……….(ii)

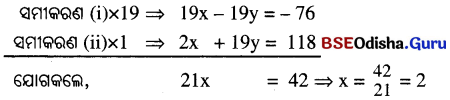
ସମୀକରଣ (i) ରେ x = 2 ସ୍ଥାପନ କଲେ, 2 – y = -4 ⇒ y = 6
∴ ସମାଧାନ (x, y) = (2, 6)।

(xi) \(\frac{x+y}{2}-\frac{x-y}{3}=8\) ⇒ \(\frac{3(x+y)-2(x-y)}{6}=8\)
⇒ 3x + 3y – 2x + 2y = 48 ⇒ x + 5y = 48 ……..(i)
ପୁନଶୃ \(\frac{x+y}{3}+\frac{x-y}{4}=11\) ⇒ \(\frac{4(x+y)+3(x-y)}{12}=11\)
⇒ 4x + 4y + 3x – 3y = 132 ⇒ 7x + y = 132 ……..(ii)

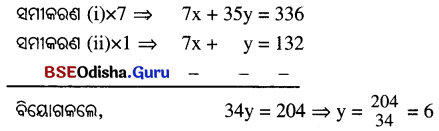
ସମୀକରଣ (i) ରେ y = 6 ସ୍ଥାପନ କଲେ, x + 5 × 6 = 48 ⇒ x = 18
∴ ସମାଧାନ (x, y) = (18, 6)।

(xii) \(\frac{x}{a}=\frac{y}{b}\) ⇒ bx = ay ⇒ bx – ay = 0 ……..(i)
ଏବଂ \(ax + by=a^2+b^2 \) ………(ii)

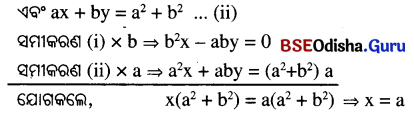
x ର ମାନ ସମୀକରଣ (i) ରେ କଲେ, ba – ay = 0 ⇒ ay = ab ⇒ y = b

ବିକଳ୍ପ ସମାଧାନ :
\(\frac{x}{a}=\frac{y}{b}=k\) (ମନେକର) x = ak, y = bk
ax + by = a² + b² = a.ak + b.bk = a² + b²
k (a² + b²) = a² + b² ⇒ k = 1
∴ x = ak = a . 1 = a; y = bk = b . 1 = b

Question 5.
ନିମ୍ନଲିଖତ ଡିଟରମିନାଣ୍ଟର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(i) \(\left|\begin{array}{ll}
2 & 5 \\
6 & 0
\end{array}\right|\)
(ii) \(\left|\begin{array}{ll}
2 & -1 \\
3 & 2
\end{array}\right|\)
(iii) \(\left|\begin{array}{ll}
0 & 4 \\
5 & -1
\end{array}\right|\)
(iv) \(\left|\begin{array}{ll}
\frac{1}{2} & 1 \\
\frac{3}{4} & \frac{1}{5}
\end{array}\right|\)
ସମାଧାନ :
(i) \(\left|\begin{array}{ll}
2 & 5 \\
6 & 0
\end{array}\right|\) = 2(0) – 6(5) = 0 – 30 = -30

(ii) \(\left|\begin{array}{ll}
2 & -1 \\
3 & 2
\end{array}\right|\) = 2 × 2 – 3 (-1) = 4 + 3 = 7

(iii) \(\left|\begin{array}{ll}
0 & 4 \\
5 & -1
\end{array}\right|\) = 0(-1) – 5 × 4 = 0 – 20 = -20

(iv) \(\left|\begin{array}{ll}
\frac{1}{2} & 1 \\
\frac{3}{4} & \frac{1}{5}
\end{array}\right|\) = \((\frac{1}{2})(\frac{1}{5})-(\frac{3}{4})(1)=\frac{1}{10}-\frac{3}{4}=\frac{2-15}{20}=\frac{-13}{20}\)

Question 6.
Cramer ଙ୍କ ନିୟମ ପ୍ରୟୋଗ କରି ନିମ୍ନ ସହସମୀକରଣମାନଙ୍କର ସମାଧାନ କର ।
(i) 2x + 3y = 5, 3x + y = 4
(ii) x + y = 3, 2x + 3y = 8
(iii) x – y = 0, 2x + y = 3
(iv) 2x – y = 3, x – 3y = -1
ସମାଧାନ :
(i) \(\Delta=\left|\begin{array}{ll}
a_1 & b_1 \\
a_2 & b_2
\end{array}\right|=\left|\begin{array}{ll}
2 & 3 \\
3 & 1
\end{array}\right|=2 \times 1-3 \times 3=2-9=-7\)
ଏଠାରେ ∆ ≠ 0 ତେଣୁ ସମୀକରଣର ସମାଧାନ ସମ୍ଭବ ।
\(∆_x=\left|\begin{array}{ll}
-c_1 & b_1 \\
-c_2 & b_2
\end{array}\right|=\left|\begin{array}{ll}
5 & 3 \\
4 & 1
\end{array}\right|=5 \times 1-4 \times 3=5-12=-7\)
\(∆_y=\left|\begin{array}{ll}
a_1 & -c_1 \\
a_2 & -c_2
\end{array}\right|=\left|\begin{array}{ll}
2 & 5 \\
3 & 4
\end{array}\right|=2 \times 4-5 \times 3=8-15=-7\)
x = \(\frac{∆_x}{∆}=\frac{-7}{-7}=1\), y = \(\frac{∆_y}{∆}=\frac{-7}{-7}=1\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (1, 1)

(ii) \(\Delta=\left|\begin{array}{ll}
a_1 & b_1 \\
a_2 & b_2
\end{array}\right|=\left|\begin{array}{ll}
1 & 1 \\
2 & 3
\end{array}\right|=1 \times 3-2 \times 1=3-2=1\)
ଏଠାରେ ∆ ≠ 0 ତେଣୁ ସମୀକରଣର ସମାଧାନ ସମ୍ଭବ ।
\(∆_x=\left|\begin{array}{ll}
-c_1 & b_1 \\
-c_2 & b_2
\end{array}\right|=\left|\begin{array}{ll}
3 & 1 \\
8 & 3
\end{array}\right|=3 \times 3-8 \times 1=9-8=1\)
\(∆_y=\left|\begin{array}{ll}
a_1 & -c_1 \\
a_2 & -c_2
\end{array}\right|=\left|\begin{array}{ll}
1 & 3 \\
2 & 8
\end{array}\right|=1 \times 8-2 \times 3=8-6=2\)
x = \(\frac{∆_x}{∆}=\frac{1}{1}=1\), y = \(\frac{∆_y}{∆}=\frac{2}{1}=2\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (1, 2)

(iii) \(\Delta=\left|\begin{array}{ll}
a_1 & b_1 \\
a_2 & b_2
\end{array}\right|=\left|\begin{array}{ll}
1 & -1 \\
2 & 1
\end{array}\right|=1 \times 1-2 \times -1=1+2=3\)
∆ ≠ 0 ତେଣୁ ସହ-ସମୀକରଣର ସମାଧାନ ସମ୍ଭବ ।
\(∆_x=\left|\begin{array}{ll}
-c_1 & b_1 \\
-c_2 & b_2
\end{array}\right|=\left|\begin{array}{ll}
0 & -1 \\
3 & 1
\end{array}\right|=0 \times 1-3 \times -1=0+3=3\)
\(∆_y=\left|\begin{array}{ll}
a_1 & -c_1 \\
a_2 & -c_2
\end{array}\right|=\left|\begin{array}{ll}
1 & 0 \\
2 & 3
\end{array}\right|=1 \times 3-2 \times 0=3-0=3\)
x = \(\frac{∆_x}{∆}=\frac{3}{3}=1\), y = \(\frac{∆_y}{∆}=\frac{3}{3}=1\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (1, 1)

(iii) \(\Delta=\left|\begin{array}{ll}
a_1 & b_1 \\
a_2 & b_2
\end{array}\right|=\left|\begin{array}{ll}
2 & -1 \\
1 & -3
\end{array}\right|=2 \times (-3)-1 \times (-1)=-6+1=-5\)
∆ ≠ 0 ତେଣୁ ସହ-ସମୀକରଣର ସମାଧାନ ସମ୍ଭବ ।
\(∆_x=\left|\begin{array}{ll}
-c_1 & b_1 \\
-c_2 & b_2
\end{array}\right|=\left|\begin{array}{ll}
3 & -1 \\
-1 & -3
\end{array}\right|=3 \times -3-(-1) \times -1=-9-1=-10\)
\(∆_y=\left|\begin{array}{ll}
a_1 & -c_1 \\
a_2 & -c_2
\end{array}\right|=\left|\begin{array}{ll}
2 & 3 \\
1 & -1
\end{array}\right|=2 \times -1-1 \times 3=-2-3=-5\)
x = \(\frac{∆_x}{∆}=\frac{-10}{-5}=1\), y = \(\frac{∆_y}{∆}=\frac{-5}{-5}=1\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (x, y) = (2, 1)