Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 4 ସମ୍ଭାବ୍ୟତା Ex 4(a) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Algebra Chapter 4 ସମ୍ଭାବ୍ୟତା Ex 4(a)
Question 1.
(i) ଗୋଟିଏ ଲୁଡୁ ଗୋଟିକୁ ଥରେ ଗଡ଼ାଗଲା । ‘ଫଳ 8’ ଆସିବାର ସମ୍ଭାବ୍ୟତା ନିରୂପଣ କର ।
(ii) ଗୋଟିଏ ଲୁଡୁଗୋଟିକୁ ଥରେ ଗଡ଼ାଗଲା । ‘ଫଳ 7ରୁ କମ୍’ ଆସିବାର ସମ୍ଭାବ୍ୟତା ନିରୂପଣ କର ।
(iii) ଗୋଟିଏ ଲୁଡୁଗୋଟି ଥରେ ଗଡ଼ାଗଲା । ‘ଫଳ ≤ 3’ ଆସିବାର ସମ୍ଭାବ୍ୟତା ନିରୂପଣ କର ।
(iv) ମିଲି ଓ ଲିମା ଟେନିସ୍ ଖେଳୁଥିଲେ । ଯଦି ଖେଳରେ ମିଲି ଜିଣିବାର ସମ୍ଭାବ୍ୟତା 0.62 ହୁଏ, ତେବେ ଲିମ୍ବା ହାରିବାର ସମ୍ଭାବ୍ୟତା ନିରୂପଣ କର ।
(v) ଦୁଇଟି ମୁଦ୍ରାକୁ ଥରେ ଟସ୍ କରାଗଲା । ‘ଫଳ ଅତିକମ୍ରେ ଗୋଟିଏ T’ ଆସିବାର ସମ୍ଭାବ୍ୟତା ସ୍ଥିର କର ।
(vi) ଗୋଟିଏ ପରୀକ୍ଷଣରେ ସମସ୍ତ ମୌଳିକ ବା ସରଳ ଘଟଣାଗୁଡ଼ିକର ସମ୍ଭାବ୍ୟତାର ସମଷ୍ଟି ସ୍ଥିର କର ।
(vii) P(E) = 0.05 ହେଲେ P(E) କେତେ ସ୍ଥିର କର ।
ସମାଧାନ:
(i) ଗୋଟିଏ ଲୁଡୁଗୋଟି ଥରେ ଗଡ଼ାଇଲେ ମୋଟ ଫଳାଫଳ ସଂଖ୍ୟା 6 ହେବ ।
8 ଲୁଡୁଗୋଟିରେ ଫଳର ବାରମ୍ବାରତା 0 ହେବ ।

(ii) ଗୋଟିଏ ଲୁଡୁଗୋଟି ଥରେ ଗଡ଼ାଇଲେ ମୋଟ ଫଳାଫଳ ସଂଖ୍ୟା 6 ହେବ ।

ଲୁଡୁଗୋଟିକୁ ଥରେ ଗଡାଗଲା । ଫଳ 7 ରୁ କମ୍ ନିଶ୍ଚିତ ଘଟଣା ହେତୁ ଉକ୍ତ ଘଟଣାର ସମ୍ଭାବ୍ୟତା = 1
P(1) = \(\frac{1}{6}\), P(2) = \(\frac{1}{6}\), P(3) = \(\frac{1}{6}\), P(4) = \(\frac{1}{6}\), P(5) = \(\frac{1}{6}\), P(6) = \(\frac{1}{6}\)
∴ P(<7) = 6 × \(\frac{1}{6}\) = 1
(iii) ଏଠାରେ ମୋଟ ଫଳାଫଳ ସଂଖ୍ୟା = 6
‘ଫଳ ≤ 3’ ଆସ।ର ସଂଖ୍ୟା = 3; (∵ ଫଳ ≤ 3 = {1, 2, 3})
∴ ଘଟଣାଉ ଉ।ଉପୃ।ରତା 3 ।
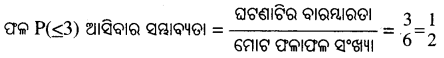
(iv) ଖେଳଟିରେ ମିଲି ଜିଣିବାର ସମ୍ଭାବ୍ୟତା 0.62 ହେଲେ, ଲିମା ହାରିବାର ସମ୍ଭାବ୍ୟତା = 1 – 0.62 = 0.38
କାରଣ ହାରିବା ବା ଜିଣିବା ଉଭୟର ସମ୍ଭାବ୍ୟତାର ସମଷ୍ଟି ।
ବି. ତ୍ର.: P(E) = 0.62 ହେଲେ, P(E) = 1 – 0.62 = 0.38
![]()
(v) ଦୁଇଟି ମୁଦ୍ରାକୁ ଥରେ ଟସ୍କକଲେ ସମ୍ଭାବ୍ୟ ସମସ୍ତ ଫଳାଫଳଗୁଡ଼ିକ HH, HT, TH, TT ।
ଏଗୁଡ଼ିକର ସଂଖ୍ୟା 4 ।
ଘଟଣା E ଅତି କମ୍ରେ ଗୋଟିଏ I ଆସିବା ଏକ ଘଟଣାଦ୍ଵାରା ଅନୁଗୃହୀତ ଫଳାଫଳଗୁଡ଼ିକ TI, TH, HT । ଏଗୁଡ଼ିକର ସଂଖ୍ୟା = 3
∴ ଫଳ ଅତିକମରେ ଗୋଟିଏ ‘T’ ଆସିବାର ସମ୍ଭାବ୍ୟତା = P (E) = \(\frac{3}{4}\)
∴ ଦୁଇଟି ମୁଦ୍ରାର ଟସ୍ରେ ଅତିକମ୍ରେ ଗୋଟିଏ T ଆସିବାର ସମ୍ଭାବ୍ୟତା = \(\frac{3}{4}\)।
(vi) ଘଟଣା E ଘଟଣା Ē ର ପରିପୂରକ ଘଟଣା । ଅର୍ଥାତ୍ P(E) + P(E) = 1
∴ ଗୋଟିଏ ପରୀକ୍ଷଣରେ ସମସ୍ତ ମୌଳିକ ବା ସରଳ ଘଟଣାଗୁଡ଼ିକର ସମ୍ଭାବ୍ୟତାର ସମଷ୍ଟି = 1
(vii) P(E) = 0.05 ହେଲେ P(E) = 1 – \( 0.0 \overline{5}\) = 0.95
କାରଣ P(E) + P(E’) = 1)
Question 2.
ଗୋଟିଏ ବାକ୍ସରେ ତିନୋଟି ନୀଳ, ଦୁଇଟି ଧଳା ଓ ଚାରୋଟି ଲାଲ ମାର୍ବଲ ରହିଛି । ସେଥୁରୁ ଗୋଟିଏ ମାର୍ବଲ ବାକ୍ସରୁ ଯଦୃଚ୍ଛା (randomly) ବଛାଗଲା । ନିମ୍ନଲିଖତ କ୍ଷେତ୍ରରେ ସମ୍ଭାବ୍ୟତା ନିରୂପଣ କର।
(i) ଗୋଟିଏ ଧଳା ମାର୍ବଲ ଆସିବାର,
(ii) ଗୋଟିଏ ନୀଳ ମାର୍ବଲ ଆସିବାର ଓ
(iii) ଗୋଟିଏ ଲାଲ୍ ମାର୍ବଲ ଆସିବାର
ସମାଧାନ:
ବାକ୍ସରେ ଥିବା ବିଭିନ୍ନ ରଙ୍ଗର ସମୁଦାୟ ମାର୍ବଲ ସଂଖ୍ୟା
(i) ଧଳା ମାର୍ବଲ ସଂଖ୍ୟା = 2
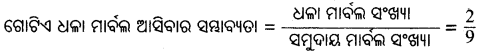
(ii) ନୀଳ ମାର୍ବଲ ସଂଖ୍ୟା = 3
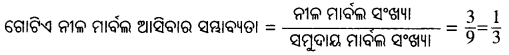
(iii) ଲାଲ୍ ମାର୍ବଲ ସଂଖ୍ୟା = 4
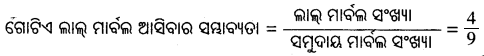
Question 3.
ଗୋଟିଏ ବ୍ୟାଗରେ ପାଞ୍ଚଟି ଧଳା, ଚାରୋଟି ଲାଲ୍ ଏବଂ ତିନୋଟି କଳା ଏକ ଆକୃତିବିଶିଷ୍ଟ ବଲ୍ ରହିଛି । ନିମ୍ନଲିଖତ କ୍ଷେତ୍ରରେ ସମ୍ଭାବ୍ୟତା ନିରୂପଣ କର ।
(i) ଗୋଟିଏ ଧଳାବଲ୍ ନ ଆସିବାର
(ii) ଗୋଟିଏ ଲାଲ୍ ବଲ୍ ନଆସିବାର
(iii) ଗୋଟିଏ ଧଳାବଲ୍ ନ ଆସିବାର
ସମାଧାନ:
ବ୍ୟାଗରେ ଥିବା ବିଭିନ୍ନ ରଙ୍ଗର ଏକ ଆକୃତି ବିଶିଷ୍ଟ ମୋଟ ବଲ୍ ସଂଖ୍ୟା = 5 + 4 + 3 = 12
(i) ବ୍ୟାଗରେ ଥିବା କଳା ବଲ୍ର ସଂଖ୍ୟା = 3
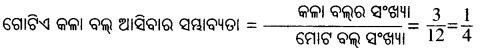
(ii) ଲାଲ୍ ବଲ୍ର ସଂଖ୍ୟା = 4
ଗୋଟିଏ ଲାଲ୍ ବଲ୍ ଆସିବାର ସମ୍ଭାବ୍ୟତା P(E) = \(\frac{4}{12}\) = \(\frac{1}{3}\)
ଗୋଟିଏ ଲାଲ୍ ବଲ୍ ନ ଆସିବାର ସମ୍ଭାବ୍ୟତା = P(E) = 1 – P(E) = 1 – \(\frac{1}{3}\) – \(\frac{2}{3}\)
(iii) ଧଳା ବଲ୍ ସଂଖ୍ୟା = 5
ଗୋଟିଏ ଧଳା ବଲ୍ ଆସିବାର ସମ୍ଭାବ୍ୟତା E = \(\frac{5}{12}\)
ଗୋଟିଏ ଧଳା ବଲ୍ ନ ଆସିବାର ସମ୍ଭାବ୍ୟତା E = 1 – E = 1 – \(\frac{5}{12}\) = \(\frac{7}{12}\)।
![]()
Question 4.
ଗୋଟିଏ ବାକ୍ସରେ 60 ବୈଦ୍ୟୁତିକ ବଲ୍ବ ଅଛି । ସେଥିରୁ 12ଟି ଖରାପ ଏବଂ ଅନ୍ୟ ସମସ୍ତ ଭଲ ବଲ୍ବ । ସେଥ୍ ମଧ୍ୟରୁ ଗୋଟିଏ ବଲ୍ବ ଯଦୃଚ୍ଛା ବାହାର କରାଗଲା । ନିମ୍ନଲିଖତ କ୍ଷେତ୍ରରେ ସମ୍ଭାବ୍ୟତା ନିରୂପଣ କର ।
(i) ଗୋଟିଏ ଭଲ ବଲ୍ବ ବାହାରିବା
(ii) ଗୋଟିଏ ଖରାପ ବଲ୍ବ ବାହାରିବା
ସମାଧାନ:
ଗୋଟିଏ ବାକ୍ସରେ 60ଟି ବୈଦ୍ୟୁତିକ ବଲ୍ବ ଅଛି।
ସେଥୁରୁ 12ଟି ଖରାପ ବଲ୍ବ।
ଭଲ ବଲ୍ବର ସଂଖ୍ୟା 60 – 12 = 48

