Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 5 ପରିସଂଖ୍ୟାନ Ex 5(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Algebra Chapter 5 ପରିସଂଖ୍ୟାନ Ex 5(b)
(କ – ବିଭାଗ )
(a) ନିମ୍ନଲିଖ ଉକ୍ତିମାନଙ୍କ ମଧ୍ୟରୁ ଯେଉଁଟି ଠିକ୍ ତା’ ପାଖରେ T ଓ ଯେଉଁଟି ଭୁଲ ତା’ ପାଖରେ F ଲେଖ ।
(i) ଯେକୌଣସି ତଥ୍ୟାବଳୀର ମଧ୍ୟମା, ସେହି ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ସହ ସମାନ ।
(ii) ବଡ଼ରୁ ସାନ କ୍ରମାନୁସାରେ ଲେଖାଥିବା 13ଟି ଲବ୍ଧାଙ୍କ ବିଶିଷ୍ଟ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ଏହାର ଆରମ୍ଭରୁ ସପ୍ତମ ସ୍ଥାନରେ ଥିବା ଲବ୍ଧାଙ୍କ ସହ ସମାନ ।
(iii) କୌଣସି ଏକ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ସର୍ବଦା ଉକ୍ତ ତଥ୍ୟାବଳୀ ଲବ୍ଧାଙ୍କମାନଙ୍କ ମଧ୍ୟରୁ ଗୋଟିଏ ।
(iv) 30 ଟି ଲବ୍ଧାଙ୍କ ଥିବା ତଥ୍ୟାବଳୀର ମଧ୍ୟମା 15 ।
(v) 5,8, 3, 7, 11, 27, 16 ସହି ତଥ୍ୟାବଳୀର ମଧ୍ୟମା 8 ।
ଉ –
(i) F, (ii) T, (iii) F, (iv) F, (v) T
(b) ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ପ୍ରଦାନ କର ।
(a) ପ୍ରଥମ ନଅଗୋଟି ଗଣନ ସଂଖ୍ୟାର ମଧ୍ୟମା କେତେ ?
(b) ପ୍ରଥମ ଦଶଗୋଟି ମୌଳିକ ସଂଖ୍ୟାର ମଧ୍ୟମା କେତେ ?
(c) ସମସ୍ତ ‘x’ର ମଧ୍ୟମା ସ୍ଥିର କର ଯେତେବେଳେ 1 ≤ x < 7 ।
(d) 7, 3, 10, 5, x ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ‘x’ ହେଲେ xର ମାନ ସ୍ଥିର କର (x ∈ N) ।
(e) ପ୍ରଥମ 6 ଗୋଟି ଗଣନ ସଂଖ୍ୟାର ମଧ୍ୟମା ପ୍ରଥମ 7 ଗୋଟି ଗଣନ ସଂଖ୍ୟାର ମଧ୍ଯମାଠାରୁ କେତେ କମ୍ ?
ଉ –
(a) ପ୍ରଥମ ନଅଗୋଟି ଗଣନ ସଂଖ୍ୟା – 1, 2, 3, 4, 5, 6, 7, 8, 9 ।
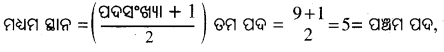
5ମ ସ୍ଥାନର ସ୍ଥାନୀୟ ଲବ୍ଧାଙ୍କ = 5
∴ ମଧ୍ୟମା = 5
(b) ପ୍ରଥମ ଦଶଗୋଟି ମୌଳିକ ସଂଖ୍ୟା – 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
ଏଠାରେ ପଦସଂଖ୍ୟା = 10
ମଧ୍ୟମା ସ୍ଥାନ \(\frac{10}{2}\) = 5ମ ସ୍ଥାନ ଓ 5 + 1 = 6ଷ୍ଠ ସ୍ଥାନ
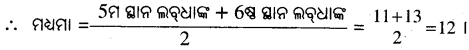
(c) ତଥ୍ୟାବଳୀଟି 1 ≤ x < 7 ⇒ 1, 2, 3, 4, 5, 6 1 ∴ ମଧ୍ୟମା = \(\frac{3+4}{2}\) = 3.5
(d) 7, 3, 10, 5, x ତଥ୍ୟାବଳୀର ମଧ୍ୟମା x (x ∈ N) ।
ସାନରୁ ବଡ଼ କ୍ରମରେ ସଜାଇଲେ 3, 5, x, 7, 10 ।
∴ x, 5 ଓ 7ର ମଧ୍ୟବର୍ତ୍ତୀ ଗଣନ ସଂଖ୍ୟା = 6
ମଧ୍ୟମା (Md) = 6
(e) ପ୍ରଥମ 6ଟି ଗଣନ ସଂଖ୍ୟାର ମଧ୍ୟମା = \(\frac{3+4}{2}\) = 3.5
ପ୍ରଥମ 7ଟି ଗଣନ ସଂଖ୍ୟାର ମଧ୍ୟମା = 4 ∴ 4 – 3.5 = 0.5
∴ ପ୍ରଥମ 6 ଗୋଟି ଗଣନ ସଂଖ୍ୟାର ମଧ୍ୟମା ପ୍ରଥମ 7 ଗୋଟି ଗଣନ ସଂଖ୍ୟାର ମଧ୍ଯମାଠାରୁ 0.5 କମ୍ ।
![]()
(ଖ – ବିଭାଗ )
Question 2.
ଦତ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କର ।
(i) 7, 8, 4, 3, 10
(ii) 11, 27, 36, 58, 65, 72, 80, 95
(iii) 7, 12, 15, 6, 20, 8, 4, 10
(iv) 18, 32, 37, 25, 31, 19, 25, 29, 31
ସମାଧାନ :
(i) ଦତ୍ତ ତଥ୍ୟାବଳୀକୁ ଊର୍ଦ୍ଧ୍ବକ୍ରମରେ ସଜ୍ଜିତ କଲେ ହେବ – 3, 4, 7, 8, 10 ।
ଲବ୍ଧାଙ୍କମାନଙ୍କର ସଂଖ୍ୟା = 5
ତଥ୍ୟାବଳୀର ମଧ୍ୟମା (Md) = \(\frac{5+1}{2}\) ତମ ସ୍ଥାନ = 3ୟ ଲବ୍ଧାଙ୍କ ଅର୍ଥାତ୍ ମଧ୍ୟମା (Md) = 7
(ii) 11,27, 36, 58, 65, 72, 80, 95 (ଏଠାରେ ଆଠଟି ଲବ୍ଧାଙ୍କ ଊର୍ଦ୍ଧ୍ବକ୍ରମରେ ସଜ୍ଜିତ)
ଫଳରେ ମଧ୍ୟମ ଲବ୍ଧାଙ୍କ ଦ୍ବୟ \(\frac{8}{2}\) = 4ର୍ଥ ଲବ୍ଧାଙ୍କ, \(\frac{8}{2}\) + 1 = 4 + 1 = 5ମ ଲବ୍ଧାଙ୍କ
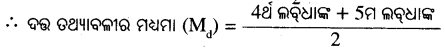
= \(\frac{58+65}{2}=\frac{123}{2}\) = 61.5
(iii) ଲବ୍ଧାଙ୍କଗୁଡ଼ିକୁ ଊର୍ଦ୍ଧ୍ବକ୍ରମରେ ସଜ୍ଜିତ କଲେ – 4, 6, 7, 8, 10, 12, 15, 20 ।
ଲବ୍ଧାଙ୍କ ସଂଖ୍ୟା = 8
ଫଳରେ ମଧ୍ୟମ ଲବ୍ଧାଙ୍କ ଦ୍ବୟ \(\frac{8}{2}\) = 4ର୍ଥ ଲବ୍ଧାଙ୍କ, 4 + 1 = 5ମ ଲବ୍ଧାଙ୍କ

(iv) ନଅଟି ଲବ୍ଧାଙ୍କଗୁଡ଼ିକୁ ଊର୍ଦ୍ଧ୍ବକ୍ରମରେ ସଜ୍ଜିତ କଲେ – 18, 19, 25, 25, 29, 31, 31, 32, 37
ଲବ୍ଧାଙ୍କ ସଂଖ୍ୟା = 9
ମଧ୍ୟମ ଲବ୍ଧାଙ୍କ = \(\frac{9+1}{2}\) = 5ମ ଲବ୍ଧାଙ୍କ ∴ ମଧ୍ୟମା (Md) = 29 ।
Question 3.
(i) ନିମ୍ନ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ସ୍ଥିର କର ।
| ଲବ୍ଧାଙ୍କ (x) | 11 | 12 | 13 | 14 | 15 | 16 |
| ବାରମ୍ବାରତା (f) | 2 | 4 | 6 | 10 | 8 | 7 |
ସମାଧାନ :
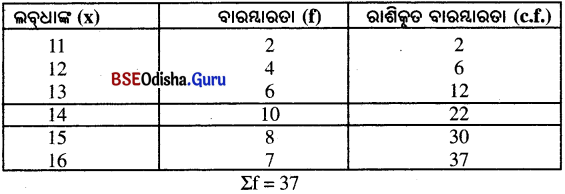
ଏଠାରେ ମୋଟ ଲବ୍ଧାଙ୍କ n ଅଯୁଗ୍ମ ହୋଇଥିବାରୁ ମଧ୍ୟମ ଲବ୍ଧାଙ୍କର ସ୍ଥାନ (m)
\(\frac{n+1}{2}=\frac{37+1}{2}=\frac{38}{2}\) = 19 ତମ ସ୍ଥାନ
19ଠାରୁ ଠିକ୍ ବୃହତ୍ତର ରାଶିକୃତ ବାରମ୍ବାରତା = 22
(ii)
| ଲବ୍ଧାଙ୍କ (x) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ବାରମ୍ବାରତା (f) | 5 | 8 | 15 | 24 | 14 | 9 | 5 | 4 |
ସମାଧାନ :
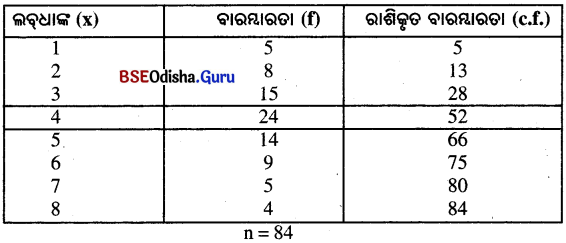
n = 84
84
∴ ମଧ୍ଯମ ସ୍ଥାନ = \(\frac{84}{2}\) = 42 ତମ ସ୍ଥାନ । 42 ଠାରୁ ଠିକ୍ ବୃହତ୍ତର ରାଶିକୃତ ବାରମ୍ବାରତା 52 ।
∴ 52 ତମ ସ୍ଥାନର ସ୍ଥାନୀୟ ଲବ୍ଧାଙ୍କ 4 ।
∴ ମଧ୍ୟମା (Mn) = 4
![]()
(iii) ନିମ୍ନ ସାରଣୀରେ 80 ଜଣ ଛାତ୍ରଙ୍କର ଗଣିତ ବିଷୟରେ ପାଇଥିବା ନମ୍ବର ଦିଆଯାଇଛି । ଉକ୍ତ ତଥ୍ୟାବଳୀ ମଧ୍ୟମା ସ୍ଥିର କର ।
| ଗଣିତରେ ରଖୁଥିବା ନମ୍ବର (x) | 10ରୁ କମ୍ | 20ରୁ କମ୍ | 30ରୁ କମ୍ | 40ରୁ କମ୍ | 50ରୁ କମ୍ | 60ରୁ କମ୍ |
| ଛାତ୍ରସଂଖ୍ୟା (c.f.) | 3 | 12 | 27 | 57 | 75 | 80 |
ସମାଧାନ :
| ଲବ୍ଧାଙ୍କ (x) | ବାରମ୍ବାରତା (f) | ରାଶିକୃତ ବାରମ୍ବାରତା (c.f.) |
| 0-10 | 3 | 3 |
| 10-20 | 9 | 12 |
| 20-30 | 15 | 27 |
| 30-40 | 30 | 57 |
| 40-50 | 18 | 75 |
| 50-60 | 05 | 80 |
| n=80 |
ଏଠାରେ ମଧ୍ୟମ ସ୍ଥାନ (m) = \(\frac{n}{2}=\frac{80}{2}\) = 40
40 ଠାରୁ ଠିକ୍ ବୃହତ୍ତର ରାଶିକୃତ ବାରମ୍ବାରତା = 57
ମଧ୍ୟମା ସଂଭାଗ ହେଲା : (30 – 40)
l = 30, f = 30, c = 27, i = 40 – 30 = 10
ମଧ୍ୟମା (Md) = l + \(\frac{m-c}{f}\) × i = 30 + \(\frac{40-27}{30}\) × 10 = 30 + \(\frac{13}{3}\) = 30 + 4.3 = 34.3
Question 4.
ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ସଂଭାଗ ସ୍ଥିର କର ।
| ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ | 55 | 65 | 75 | 85 | 95 | 105 | 115 | 125 | 135 |
| ବାରମ୍ବାରତା | 4 | 21 | 35 | 42 | 70 | 28 | 10 | 25 | 15 |
ସମାଧାନ :
| ସଂଭାଗ (x) | ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ | ବାରମ୍ବାରତା (f) | ରାଶିକୃତ ବାରମ୍ବାରତା c.f. |
| 50-60 | 55 | 4 | 4 |
| 60-70 | 65 | 21 | 25 |
| 70-80 | 75 | 35 | 60 |
| 80-90 | 85 | 42 | 102 |
| 90-100 | 95 | 70 | 172 |
| 100-110 | 105 | 28 | 200 |
| 110-120 | 115 | 10 | 210 |
| 120-130 | 125 | 25 | 235 |
| 130-140 | 135 | 15 | 250 |
| n = Σf = 250 |
ଏଠାରେ ମଧ୍ୟମ ସ୍ଥାନ (m) = \(\frac{n}{2}=\frac{250}{2}\) = 125,
125 ଠାରୁ ଠିକ୍ ବୃହତ୍ତର ରାଶିକୃତ ବାରମ୍ବାରତା = 172
ମଧ୍ୟମା ସଂଭାଗ = 90 – 100
l = 90, m = 125, f = 70, c = 102, i = 100 – 90 = 10
ମଧ୍ୟମା (Md) = l + \(\frac{m-c}{f}\) × i = 90 + \(\frac{125-102}{30}\) × 10 = 90 + \(\frac{23}{7}\) = 90 + 3.3 = 93.3
Question 5.
ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ସଂଭାଗ ସ୍ଥିର କର ।
| ଉଚ୍ଚତା ସେ.ମି. | 0ରୁ ଅଧ୍ଵ | 10ରୁ ଅଧ୍ଵ | 20ରୁ ଅଧ୍ଵ | 30ରୁ ଅଧ୍ଵ | 40ରୁ ଅଧ୍ବକ |
| ଗସ୍ଥ | 55 | 50 | 40 | 20 | 5 |
ସମାଧାନ :
| ସଂଭାଗ (x) | ବାରମ୍ବାରତା (f) | ରାଶିକୃତ ବାରମ୍ବାରତା c.f. |
| 50-40 | 5 | 5 |
| 40-30 | 15 | 20 |
| 30-20 | 20 | 40 |
| 20-10 | 10 | 50 |
| 10-0 | 5 | 55 |
| N=Σf=55 |
ଏଠାରେ m = \(\frac{55}{2}\) = 27.5, 28 ଠାରୁ ଠିକ୍ ବୃହତ୍ତର ରାଶିକୃତ ବାରମ୍ବାରତା = 40
ମଧ୍ୟମା ସଂଭାଗ = 20 -30 ।
∴ l = 30, f = 20, c = 20, i = 20 – 30 = -10
Md = l + \(\frac{m-c}{f}\) × i = 30 + \(\frac{27.5-20}{20}\) × (-10) = 30 + \(\frac{7.5}{2}\) = 30 – 3.75 = 26.25
∴ ମଧ୍ୟମା ସଂଭାଗ = 20 – 30, ମଧ୍ୟମା = 26.25
![]()
(ଗ – ବିଭାଗ )
Question 6.
ନିମ୍ନ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କର ।
| ସଂଭାଗ | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| ବାରମ୍ବାରତା | 4 | 9 | 15 | 14 | 8 |
ସମାଧାନ :
| ସଂଭାଗ (x) | ବାରମ୍ବାରତା (f) | ରାଶିକୃତ ବାରମ୍ବାରତା c.f. |
| 0-10 | 4 | 4 |
| 10-20 | 9 | 13 |
| 20-30 | 15 | 28 |
| 30-40 | 14 | 42 |
| 40-50 | 8 | 50 |
| N=Σf=50 |
ଏଠାରେ n = 50, m = \(\frac{50}{2}\) = 25, 25 ଠାରୁ ଠିକ୍ ବୃହତ୍ତର ରାଶିକୃତ ବାରମ୍ବାରତା = 28
ମଧ୍ୟମା ସଂଭାଗ = 20 – 30 । ସଂଭାଗ (i) = 30 – 20 = 10
∴ l = 20, f = 15, c = 13,
Md = l + \(\frac{m-c}{f}\) × i = 20 + \(\frac{25-13}{15}\) × 10 = 20 + \(\frac{120}{15}\) = 20 + 8 = 28
∴ ମଧ୍ୟମା = 28
Question 7.
ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ତୁମେ ଜାଣିଥିବା ଉଭୟ ପ୍ରଣାଳୀରେ ନିର୍ଣ୍ଣୟ କର । ଉତ୍ତର ଦ୍ବୟ ମଧ୍ୟରେ କ’ଣ ସମ୍ପର୍କ ରହିଛି ଦେଖ ।
| ଲବ୍ଧାଙ୍କ (x) | 2 | 5 | 6 | 7 | 8 | 9 | 10 |
| ବାରମ୍ବାରତା (f) | 8 | 12 | 21 | 31 | 18 | 13 | 5 |
ସମାଧାନ :
ପ୍ରଥମ ପ୍ରଣାଳୀ :
| ଲବ୍ଧାଙ୍କ (x) | 2 | 5 | 6 | 7 | 8 | 9 | 10 |
| ବାରମ୍ବାରତା (f) | 8 | 12 | 21 | 31 | 18 | 13 | 5 |
| ରାଶିକୃତ ବାରମ୍ବାରତା | 8 | 20 | 41 | 72 | 90 | 103 | 108 |
ମଧ୍ୟମ ଲବ୍ଧାଙ୍କର ସ୍ଥାନ (m) = \(\frac{n+1}{2}=\frac{108+1}{2}=54.8\)
54.5 ଠାରୁ ଠିକ୍ ବୃହତ୍ତର ରାଶିକୃତ ବାରମ୍ବାରତା ହେଲା 72 । ∴ ମଧ୍ୟମା = 7 (ପ୍ରାୟ)
ଦ୍ଵିତୀୟ ପ୍ରଣାଳୀ :
| ଲବ୍ଧାଙ୍କ (x) | 2 | 5 | 6 | 7 | 8 | 9 | 10 |
| ବାରମ୍ବାରତା (f) | 8 | 12 | 21 | 31 | 18 | 13 | 5 |
| ରାଶିକୃତ ବାରମ୍ବାରତା | 8 | 20 | 41 | 72 | 90 | 103 | 108 |
ମାଧ୍ୟମ ସ୍ଥାନ (m) = \(\frac{108}{2}\) = 54
ଅଙ୍କିତ ଲେଖ (ogive) ଉପରେ P ଏକ ବିନ୍ଦୁ ସ୍ଥାପନ କରାଯାଇଛି ।
ଯାହାର y – ସ୍ଥାନାଙ୍କ = 54 (ମଧ୍ୟମ ସ୍ଥାନ) । ପୁନଶ୍ଚ P ବିନ୍ଦୁରୁ X – ଅକ୍ଷ ପ୍ରତି ଲମ୍ବ ଅଙ୍କନ କରାଯାଇ P ବିନ୍ଦୁର x – ସ୍ଥାନାଙ୍କ ନିରୂପଣ କରାଯାଇଛି ।
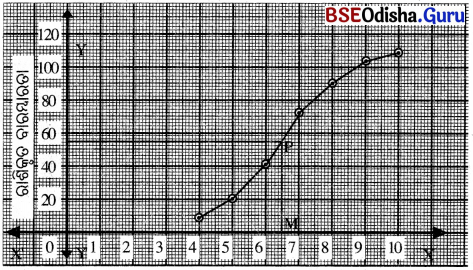
ଏଠାରେ x – ସ୍ଥାନାଙ୍କ = 65
ଦଉ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା = 6:5 (ପ୍ରାୟ)
ଉତ୍ତର ଦ୍ବୟର ପାର୍ଥକ୍ୟ = 7 – 6.5 = 0.5
Question 8.
ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କର ।
| ସଂଭାଗ (x) | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| ବାରମ୍ବାରତା (f) | 5 | 12 | 22 | 18 | 10 | 6 |
ସମାଧାନ :
| ସଂଭାଗ (x) | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| ବାରମ୍ବାରତା (f) | 5 | 12 | 22 | 18 | 10 | 6 |
| ରାଶିକୃତ ବାରମ୍ବାରତା(c.f.) | 5 | 17 | 39 | 57 | 67 | 73 |
∴ ମଧ୍ୟମା ସ୍ଥାନ = m = \(\frac{73+1}{2}\) = 37 । m ଠାରୁ ଠିକ୍ ବୃହତ୍ତର ରାଶିକୃତ ବାରମ୍ବାରତା = 39
∴ ମଧ୍ୟମା ସଂଭାଗ (20 – 30). ଏଠାରେ, l1= 20, l2 = 30
ମଧ୍ୟମା ସଂଭାଗର ବାରମ୍ବାରତା = f = 22
ମଧ୍ୟମା ସଂଭାଗର ଠିକ୍ ପୂର୍ବବର୍ତ୍ତୀ ସଂଭାଗର ରାଶିକୃତ ବାରମ୍ବାରତା = c = 17
ମଧ୍ୟମା = l1 + \(\frac{m-c}{f}\) (l1 – l2)
= 20 + \(\frac{37-17}{22}\) (30 – 20) = 20 + \(\frac{20×10}{22}\) = 20 + 9.1 = 29.1 (ପ୍ରାୟ)
![]()
Question 9.
ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ରାଶିକୃତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶ ଲେଖଚିତ୍ର ଅଙ୍କନ କର ଓ ଏହା ସାହାଯ୍ୟରେ
(i) ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କର ଏବଂ
(ii) 65% ରୁ ଅଧ୍ଵ ନମ୍ବର ରଖୁଥିବା ଛାତ୍ର ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କର ।
| ନମ୍ବର : | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| ବାରମ୍ବାରତା | 5 | 10 | 20 | 25 | 15 | 12 | 9 | 8 |
ସମାଧାନ : (i)
| ନମ୍ବର : | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| ବାରମ୍ବାରତା (f) | 5 | 10 | 20 | 25 | 15 | 12 | 9 | 8 |
| ରାଶିକୃତ ବାରମ୍ବାରତା (c.f.) | 5 | 15 | 35 | 60 | 75 | 87 | 96 | 104 |
ମଧ୍ୟମ ସ୍ଥାନ = \(\frac{1}{2} {\frac{104}{2}+(\frac{104}{2})}\) = \(\frac{1}{2}\) (52+53) = \(\frac{1}{2}\) × 105 = 52.5
ମଧ୍ୟମା ନିଶ୍ଚୟ : ରାଶିକୃତ ବାରମ୍ବାରତା c.f, ନିର୍ଦ୍ଦେଶକ ଅକ୍ଷରେ 52.5 ଏକକ ଚିହ୍ନ ପାଖରେ ଅକ୍ଷ ପ୍ରତି ଗୋଟିଏ ଲମ୍ବ ଅଙ୍କନ କର ।
ଏହାର ରାଶିକୃତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶ ଲେଖକୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ ତାହାର ନାମ ‘P’ ନିଅ ।
‘P’ ବିନ୍ଦୁରୁ ଲବ୍ଧାଙ୍କ ନିର୍ଦ୍ଦେଶ ପ୍ରତି ଏକ ଲମ୍ବ ଅଙ୍କନ କର, ତାହାର ନାମ M ଦିଅ ।
∴ M ଦ୍ଵାରା ନିର୍ଦ୍ଦେଶିତ ଲବ୍ଧାଙ୍କ M = 37 (ପ୍ରାୟ)
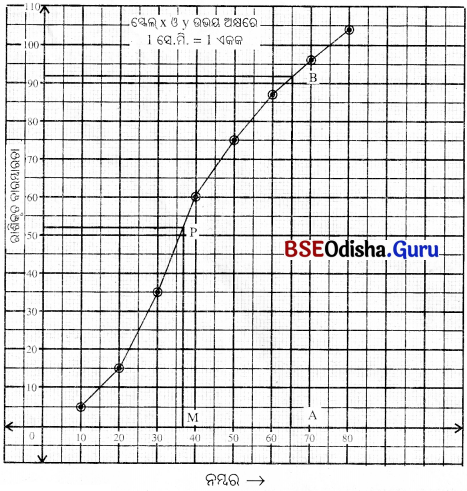
(ii) 100 ର 65% = 65
x ଅକ୍ଷରେ ଏକ ବିନ୍ଦୁ A ନିର୍ଣ୍ଣୟ କର ଯାହାର ଲବ୍ଧାଙ୍କ 65% ।
A ବିନ୍ଦୁରୁ ଉଲମ୍ବ ସରଳରେଖା ଅଙ୍କନ କର ଯାହା ଲେଖଚିତ୍ରକୁ ‘B’ ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
B ବିନ୍ଦୁରୁ ଏକ ଆନୂଭୂମିକ ସରଳରେଖା ଅଙ୍କନ କର; ଯାହା y-ଅକ୍ଷକୁ ୯ ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
‘C’ ବିନ୍ଦୁରୁ ନିର୍ଦ୍ଦେଶ ସଂଖ୍ୟା = 92
∴ 65%ରୁ ଅଧ୍ଵ ନମ୍ବର ପାଇଥିବା ଛାତ୍ରଛାତ୍ରୀ ସଂଖ୍ୟା 104 – 92 = 12
Question 10.
ନିମ୍ନ ତଥ୍ୟାବଳୀକୁ ନେଇ ରାଶିକୃତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶ ଲେଖ ଅଙ୍କନ କରି ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କର ।
| ସଂଭାଗ | 0-8 | 8-16 | 16-24 | 24-32 | 32-40 | 40-48 | 48-56 |
| ବାରମ୍ବାରତା | 4 | 8 | 14 | 23 | 15 | 11 | 5 |
ସମାଧାନ :
| ସଂଭାଗ | 0-8 | 8-16 | 16-24 | 24-32 | 32-40 | 40-48 | 48-56 |
| ବାରମ୍ବାରତା | 4 | 8 | 14 | 23 | 15 | 11 | 5 |
| ରାଶିକୃତ ବାରମ୍ବାରତା | 4 | 12 | 28 | 49 | 64 | 75 | 80 |
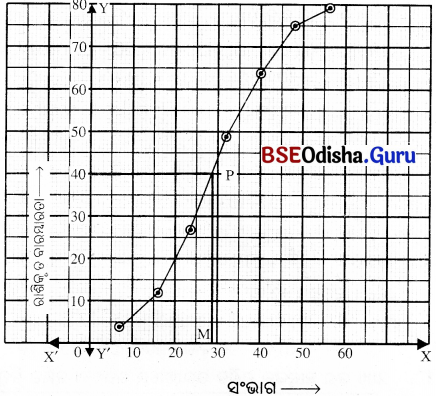
ମଧ୍ୟମ ସ୍ଥାନ (m) = \(\frac{80}{2}\) = 40
ଅଙ୍କିତ ଲେଖ (ogive) ଉପରେ P ଏକ ବିନ୍ଦୁ ଯାହାର y- ସ୍ଥାନଙ୍କ = 40
P ବିନ୍ଦୁରୁ x- ଅକ୍ଷରେ ଲମ୍ବ PM ଅଙ୍କନ କରି P ବିନ୍ଦୁର x- ସ୍ଥାନଙ୍କ ସ୍ଥିର କରାଯାଇଛି ।
P ବିନ୍ଦୁର x ସ୍ଥାନାଙ୍କ = 29 ।
ମଧ୍ୟମା = 29
![]()
Question 11.
ନିମ୍ନ ତଥ୍ୟାବଳୀରେ ଥିବା କେତେକ ସଂଭାଗର ବାରମ୍ବାରତା ଦିଆଯାଇନାହିଁ । ଯଦି ବାରମ୍ବାରତାମାନଙ୍କର ସମଷ୍ଟି 74 । ତଥ୍ୟାବଳୀର ମଧ୍ୟମା 36 ହୋଇଥାଏ, ତେବେ ଆମକୁ ଜଣା ନଥିବା ଦୁଇ ସଂଭାଗର ବାରମ୍ବାରତା ସ୍ଥିର କର ।
| ଲବ୍ଧାଙ୍କ : | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| ବାରମ୍ବାରତା | 2 | 8 | ? | 20 | 12 | ? | 4 | 3 |
ସମାଧାନ :
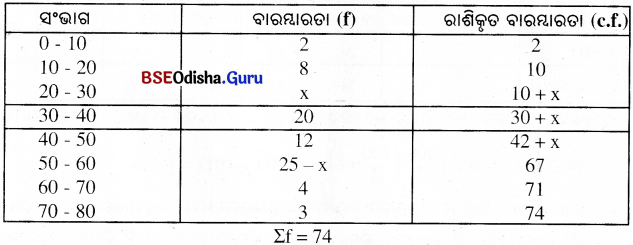
ମନେକର (20-30) ସଂଭାଗର ବାରମ୍ବାରତା = x
ସାରଣୀ 40 – 50 ସଂଭାଗର ରାଶିକୃତ ବାରମ୍ବାରତା = 42 + x
ଦତ୍ତ ଅଛି 50 – 60 ସଂଭାଗର ରାଶିକୃତ ବାରମ୍ବାରତା = 67
50-60 ସଂଭାଗ ବାରମ୍ବାରତା = 67 – (42 + x) = 25 – x
ଏଠାରେ ମଧ୍ୟମ ସ୍ଥାନ (m) = \(\frac{74}{2}\) = 37 ତମ ସ୍ଥାନ
ମଧ୍ୟମା = 36 (ଦତ୍ତ), ମଧ୍ୟମା ସଂଭାଗ = 30 – 40 l1= 30, l2 = 40
i = l1 – l2 = 40 – 30 = 10 ଓ c = 10 + x
ମଧ୍ୟମା = l + \(\frac{m-c}{f}\) × i
⇒ 36 = 30 + \(\frac{37-(10+x)}{20}\) × 10
⇒ 36 -30 = \(\frac{37-10-x}{2}\)
⇒ 6 = \(\frac{27-x}{2}\) ⇒ 12 = 27 – x
⇒ x = 27 – 12 = 15
∴ (20 – 30) ସଂଭାଗର ବାରମ୍ବାରତା = 15
ଏବଂ (50 – 60) ସଂଭାଗର ବାରମ୍ବାରତା = 25
![]()
Question 12.
200 ଜଣ ଛାତ୍ରଙ୍କର ଗଣିତ ପରୀକ୍ଷାରେ ରଖିଥିବା ନମ୍ବର ନିମ୍ନ ସାରଣୀରେ ଶତକଡ଼ାରେ ଦିଆଯାଇଛି ।
| ନମ୍ବର ଶତକଡ଼ାରେ : | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 |
| ଛାତ୍ର ସଂଖ୍ୟା : | 6 | 12 | 20 | 46 | 57 | 37 | 15 | 7 |
(i) ରାଶିକୃତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ଲେଖ ଅଙ୍କନ କରି ମଧ୍ୟମ ନିର୍ଣ୍ଣୟ କର ।
(ii) ଗଣିତରେ 45% ନମ୍ବର ହାସଲ କରିଥିବା ଛାତ୍ର ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
| ନମ୍ବର ଶତକଡ଼ାରେ | 9.5-19.5 | 19.5-29.5 | 29.5-39.5 | 39.5-49.5 | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 |
| ବାରମ୍ବାରତା (f) | 6 | 12 | 20 | 46 | 57 | 37 | 15 | 7 |
| ରାଶିକୃତ ବାରମ୍ବାରତା (c.f.) | 6 | 18 | 38 | 84 | 141 | 178 | 193 | 200 |
[ବି.ଦ୍ର. : ଅନ୍ତର୍ଭୁକ୍ତ ସଂଭାଗୀକରଣ ବ୍ୟବସ୍ଥାର ଥିବା ତଥ୍ୟାବଳୀକୁ ବହିର୍ଭୁକ୍ତ ସଂଭାଗୀକରଣ ବ୍ୟବସ୍ଥାରେ ପ୍ରକାଶ କରାଯାଇଛି ।]
ମଧ୍ୟମ ସ୍ଥାନ (m) = \(\frac{1}{2}\)(\(\frac{200}{2}+\frac{200}{2}+1\)) = \(\frac{1}{2}\)(100+101) = 100.5
(i) ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ : ରାଶିକୃତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ଲେଖ ଉପରେ 100.5 ଚିହ୍ନ ପାଖରେ ଅକ୍ଷ ପ୍ରତି ଲମ୍ବ ଅଙ୍କନ କର । ଏହା ରାଶିକୃତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ଲେଖକୁ ‘P’ ବିନ୍ଦୁରେ ଛେଦ କରୁ । ‘P’ ବିନ୍ଦୁରୁ ଲବ୍ଧାଙ୍କ ନିର୍ଦ୍ଦେଶକ ପ୍ରତି ଏକ ଲମ୍ବ ଅଙ୍କନ କର ତାହାର ନାମ M ଦିଅ ।
M ଦ୍ବାରା ନିର୍ଦ୍ଦେଶକ ଲବ୍ଧାଙ୍କ Md = 48
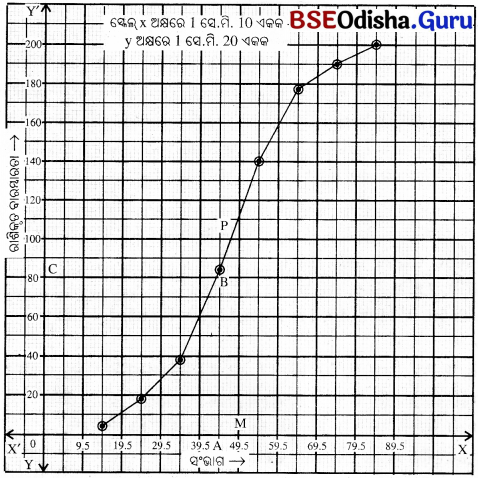
(ii) x ଅକ୍ଷରେ ଏକ ବିନ୍ଦୁ ‘A’ ନିର୍ଣ୍ଣୟ କର, ଯାହାର ଲବ୍ଧାଙ୍କ 45% ।
‘A’ ବିନ୍ଦୁରୁ ଭୂଲମ୍ବ ସରଳରେଖା ଅଙ୍କନ କର ଯାହା ଲେଖଚିତ୍ରକୁ ‘B’ ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
‘B’ ବିନ୍ଦୁରୁ ଏକ ଆନୁଭୂମିକ ସରଳରେଖା ଅଙ୍କନ କର ଯାହା y-ଅକ୍ଷକୁ ୯ ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
C ବିନ୍ଦୁରୁ ନିର୍ଦ୍ଦେଶକ ସଂଖ୍ୟା = 80
45 % ପାଇଥିବା ଛାତ୍ରସଂଖ୍ୟା = 200 – 80 = 120
