BSE Odisha 10th Class Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(a)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(a)

\(\left(\frac{{at}_1^2+{at} {t}_2^2}{2}, \frac{2 {at}_1+2 {at}_2}{2}\right)\)

Question 1.
ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ଯରେ ଦୂରତା ନିର୍ଣ୍ଣୟ କର ।
(i) (0, 0) ଓ (4, 3)
(ii) (0, 2) ଓ (-6, 2)
(iii) (-3, 0) ଓ (5, 6)
(iv) (2, 4) ଓ (1, 3)
(v) (-2, -2) ଓ (-3, -5)
(vi) (a, b) ଓ (- a, b)
ସମାଧାନ :
ମେନକର O(0, 0) ଓ P (4,3)
ମୂଳବିନ୍ଦୁଠାରୁ p(x, y)ର ଦୂରତା = \(\sqrt{x^2 + y^2}\)
OP = \(\sqrt{4^2 + 3^2}=\sqrt{16 + 9}=\sqrt{25}=5\)

(ii) ମେନକର A (0, 2), ଓ B (-6, 2)
ଏଠାରେ x₁ =0, y₁ = 2, x₂ = -6, y₂ = 2
AB = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) = √(-6-0)² +(2-2)² = √(36+0) = 6

(iii) P(-3, 0) ଓ Q (5, 6)
ଏଠାରେ x₁ = 3, y₁ = 0, x₂ = 5, y₂ = 6
PQ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)
= \(\sqrt{{5- (-3)}^2 +(6-0)^2}\) = \(\sqrt{8^2 + 6^2}\) = √64+36 = √100 = 10

(iv) P (2, 4) ଓ Q (1, 3)
PQ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) = \(\sqrt{(1-2)^2+(3-4)^2}\) = \(\sqrt{(-1)^2 +(-1)^2}\) =√2

(v) A (-2,-2) ଓ B (-3,-5).
AB = \(\sqrt{{-3-(-2)}^2 + {-5-(-2)}^2}\) = √1² +3² =√10

(vi) P (a, b) ଓ Q (a, b)
PQ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) = \(\sqrt{(-a-a)^2+{b-(-b)}^2}\)
\(\sqrt{(-2a)^2+(2b)^2}\) = \(\sqrt{4a^2+4b^2}\) = 2√(a² + b²)

Question 2.
ନିମ୍ନଲିଖ କେଉଁ ବିନ୍ଦୁଦ୍ଵୟ ମୂଳବିନ୍ଦୁ ଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ସ୍ଥିର କର ।
(i) (0, 1) ଓ (- 1, 0)
(ii) (2,3) ଓ (4, \(\frac{3}{2}\))
(iii) (√7, √19) ଓ (-√7, – √19)
(iv) (4, – 2) ଓ (2, 4)
(v) (0, 4) ଓ (2, 2)
ସମାଧାନ :
(i) ଏଠାରେ ମୂଳବିନ୍ଦୁ O(0, 0) । A (0, 1) ଓ B(- 1, 0) ।
OA = \(\sqrt{1^2+0^2}\) = 1, OB = \(\sqrt{(-1)^2 +0^2}\) = 1 ∴ OA = OB
∴ (0, 1) ଓ ( 1, 0) ମୂଳବିନ୍ଦୁ ଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

(ii) ଏଠାରେ A(2,3) ଓ B(4, \(\frac{3}{2}\))
OA = √2^2+3^2 = √4+9 = √13
OB = \(\sqrt{4² + (\frac{3}{2})²}\) = \(\sqrt{16 + \frac{9}{4}}\) = \(\sqrt{\frac{64+9}{4}}\) = \(\sqrt{\frac{1}{2}}\)
OA ≠ OB ∴ A(2, 3) ଓ B(4, \(\frac{3}{2}\)) ବିଦୁ୍ୟଦ୍ଵୟ ମୂଳବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ନୁହେଁ ।

(iii) ଏଠାରେ A (√7, √19) ଓ B (-√7,-√19) ।
OA = \(\sqrt{(√7)^2+(√19)^2}\) = \(\sqrt{7+19}\) = √26
OB = \(\sqrt{(√7)^2+(-√19)^2}\) = \(\sqrt{7+19}\) = √26
∴ OA = OB ଅର୍ଥାତ୍‌ A(√7, √19) ଓ B(-√7, -√19) ବିନ୍ଦୁଦ୍ଵୟ ମୂଳ ବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

(iv) ଏଠାରେ A (4, – 2) ଓ B (2, 4) ।
OA = \(\sqrt{4^2 +(-2)^2}\) = \(\sqrt{16+4}\) = √20 = 2√5
OB = \(\sqrt{2^2 +4^2}\) = \(\sqrt{4+16}\) = √20 = 2√5
∴ OA = OB ଅର୍ଥାତ୍‌ A(4, – 2) ଓ B(2, 4) ବିନ୍ଦୁଦ୍ଵୟ ମୂଳ ବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

(v) ଏଠାରେ A(0, 4) ଓ B(2, 2)
OA = \(\sqrt{2^2+3^2}\) = √16 = 4
OB = \(\sqrt{2² + 2²}\) = \(\sqrt{4+4}\) = √8 = 2√2.
∴ OA ≠ OB ଅର୍ଥାତ୍ A(0, 4) ଓ B(2, 2) ବିଦୁ୍ୟଦ୍ଵୟ ମୂଳ ବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ନୁହେଁ ।

Question 3.
ପ୍ରମାଣ କର ଯେ, ନିମ୍ନୋକ୍ତ ଶୀର୍ଷବିନ୍ଦୁ ବିଶିଷ୍ଟ ABC ତ୍ରିଭୁଜମାନ ସମକୋଣୀ । ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ କେଉଁ କୋଣଟି ସମକୋଣ ଦର୍ଶାଅ I
(i) A (3, 3), B (9, 0) ଓ C (12, 21)
(ii) A (1, 1), B (3, 4) ଓ C(0, 6)
(iii) A (-1, -2), B (5, -2) ଓ C (5, 6)
(iv) A (12, 8), B (- 2, 6) ଓ C (6, 0)
(v) A (1, 6), B (5, – 1) ଓ C (7, 2)
ସମାଧାନ :
P₁ = (x₁, y₁) ଓ P₂ (x₂, y₂) ହେଲେ, P₁P₂ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)

(i) A (3, 3), B (9, 0) ଓ C (12, 21)

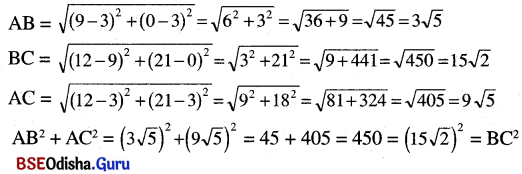
∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

(ii) A (1, 1), B (3, 4), C(0, 6)
AB = \(\sqrt{(3-1)^2+(4-1)^2}\) = \(\sqrt{2^2 +3^2}\) = √13
BC= \(\sqrt{(0-3)^2+(6-4)^2}\) = \(\sqrt{3^2 +2^2}\) = √13
AC = \(\sqrt{(0-1)^2+(6-1)^2}\) = \(\sqrt{1^2 +5^2}\) = √26
AB² + BC² = (√13)² +(√13)² = 13 + 13 = 26 = (√26)² =
∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

(iii) A (-1,- 2), B (5, -2) ଓ C (5, 6)

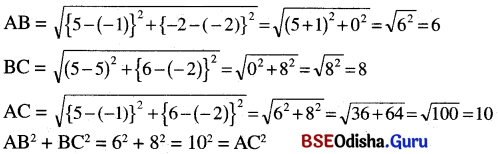
∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

(iv) A (12, 8), B (- 2, 6) ଓ C (6, 0)

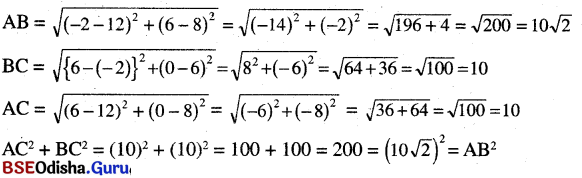
∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

(v) A (1, 6), B (5, – 1) ଓ C (7, 2)

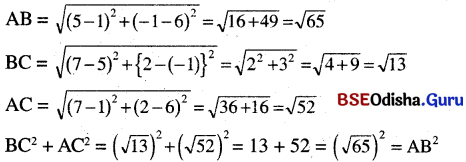
∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

Question 4.
ଦର୍ଶାଅ ଯେ ନିମ୍ନୋକ୍ତ ଶୀର୍ଷବିନ୍ଦୁ ବିଶିଷ୍ଟ ABC ତ୍ରିଭୁଜମାନ ସମଦ୍ବିବାହୁ ।
(i) A (8, 2), B(5,- 3) ଓ C (0, 0)
(ii) A (0, 6), B (- 5, 3) ଓ C (3, 1)
(iii) A (8, 9), B(- 6, 1) ଓ C (0,-5)
(iv) A (7, 1), B (11, 4) ଓ C (4, – 3)
(v) A (0, 0), B (4, 0) ଓ C (0, -4)
(vi) A (2, 2) B (- 2, 4) ଓ C (2,6)

(i) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟର ସ୍ଥାନାଙ୍କ A (8, 2), B(5, – 3), C (0, 0) ।
AB = \(\sqrt{(5-8)^2+(-3-2)^2}\) = \(\sqrt{(-3)^2 +(-5)^2}\) = \(\sqrt{9+25}\)=√34
BC = \(\sqrt{(0-5)^2+{0-(-3)}^2}\) = \(\sqrt{25+9}\) = √34
CA = \(\sqrt{(8-0)^2+(2-0)^2}\) = \(\sqrt{64+4}\) = √68 = 2√17
∴ ∆ ABCର AB = BC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(ii) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A(0, 6), B (- 5, 3) ଓ C (3, 1) ।
AB = \(\sqrt{(-5-0)^2+(3-6)^2}\) = \(\sqrt{(-5)^2 +(-3)^2}\) = \(\sqrt{25+9}\) = √34
BC= \(\sqrt{{3-(-5)}^2 +(1–3)^2}\) = \(\sqrt{8^2 +(-2)^2}\) = \(\sqrt{64+4}\)= √68
AC = \(\sqrt{(3-0)^2+(1-6)^2}\) = \(\sqrt{3^2 +(-5)^2}\) = \(\sqrt{9+25}\) = √34
∴ ∆ ABCର AB = AC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(iii) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A(8, 9), B(- 6, 1) ଓ C (0, – 5) ।
AB = \(\sqrt{(-6-8)^2 +(1-9)^2}\) = \(\sqrt{(14)^2 +(8)^2}\) = \(\sqrt{196+64}\) = √260 = 2√65
BC = \(\sqrt{{0-(-6)}2 +(-5-1)^2}\) = \(\sqrt{62+(-6)^2}\) = \(\sqrt{36+36}\) = √72 = 6√2
AC = \(\sqrt{(0-8)^2 + (-5-9)^2}\) = \(\sqrt{(-8)^2 +(-14)^2}\) = \(\sqrt{64+196}\) = √260 = 2√65
∴ ∆ ABCର AB = AC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(iv) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A (7, 1), B (11, 4) ଓ C (4, – 3) ।
AB = \(\sqrt{(11-7)^2+(4-1)^2}\) = \(\sqrt{42+32}\) = \(\sqrt{16+9}\)= √25=5
BC = \(\sqrt{(4-11)^2+(-3-4)^2}\) = \(\sqrt{(-7)^2+(-7)^2}\) = \(\sqrt{49 +49}\) = √98 = 7√2
AC = \(\sqrt{(4-7)^2 +(-3-1)^2}\) = \(\sqrt{(-3)^2 + (-4)^2}\) = \(\sqrt{9 +16}\) = √25 = 5
∴ ∆ ABCର AB = AC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(v) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A (0, 0), B (4, 0), C (0, – 4) ।
AB = \(\sqrt{4^2 +0^2}\) = \(\sqrt{16}\) = 4,
AC = \(\sqrt{0^2 +(-4)^2}\) = √16 = 4
BC= \(\sqrt{(0-4)^2+(-4-0)^2}\) = \(\sqrt{(-4)^2 +(-4)^2}\) = \(\sqrt{16+16}\) = √32 = 4√2
∴ ∆ ABCର AB = AC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(vi) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A (2, 2), B ( 2, 4) ଓ C (2, 6) ।
AB = \(\sqrt{(-2-2)^2 + (4 -2)^2}\) = \(\sqrt{4^2 +2^2}\) = \(\sqrt{16+4}\) = √20 = 2√5
BC = \(\sqrt{{2-(-2)}^2 +(6-4)^2}\) = \(\sqrt{4^2 +2^2}\) = \(\sqrt{16+4}\) = √20 = 2√5
∴ ∆ ABCର AB = BC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

Question 5.
ଦର୍ଶାଅ ଯେ ନିମ୍ନଲିଖୂତ ବିନ୍ଦୁଗୁଡ଼ିକ ପାର୍ଶ୍ଵରେ ସୂଚିତ ଚିତ୍ରକୁ ଗଠନ କରିବ ।
(i) (1, 1), (- 1, – 1), (- √3, √3) (ସମବାହୁ ତ୍ରିଭୁଜ)
(ii) (3, – 3), (- 3, 3), (3√3, 3√3) (ସମବାହୁ ତ୍ରିଭୁଜ)
(iii) (1, 2), (3, 4) ଓ (5, 8) (ସମବାହୁ ତ୍ରିଭୁଜ)
(iv) (1, 2), (2, 4) ଓ (3, 5) (ବିଷମବାହୁ ତ୍ରିଭୁଜ)
(v) (-2, 3), (8, 3) ଓ (6, 7) (ସମକୋଣୀ ତ୍ରିଭୁଜ)
(vi) (-6, -8), (-16, 12) ଓ (- 26,- 18) (ସମକୋଣୀ ସମବାହୁ ତ୍ରିଭୁଜ)
ସମାଧାନ :
(i) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(1, 1), B(- 1, – 1), ଓ C (-√3, √3) ।

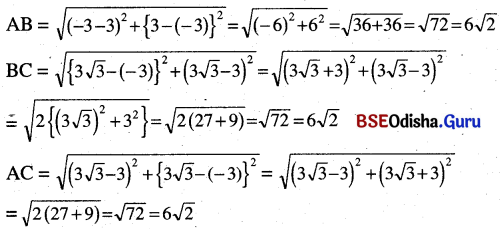
∴ ∆ ABCର AB = BC = AC । ତେଣୁ ଏହା ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।

(ii) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(3, – 3), B(- 3, 3), C(3√3, 3√3) ।

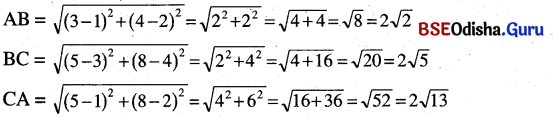
∴ ∆ ABCର AB = BC = AC । ତେଣୁ ଏହା ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।

(iii) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(1, 2), B(3, 4) ଓ C(5, 8) ।

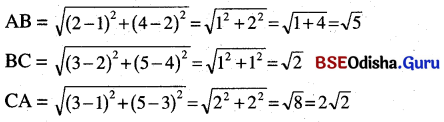
∴ ∆ ABCର AB ≠ BC ≠ AC । ତେଣୁ ଏହା ଏକ ବିଷମବାହୁ ତ୍ରିଭୁଜ ।

(iv) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(1, 2), B(2, 4) ଓ C(3, 5) ।

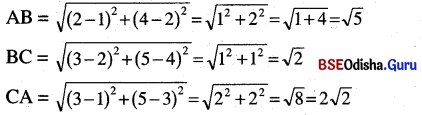
∴ ∆ ABCର AB ≠ BC ≠ AC । ତେଣୁ ABC ଏକ ବିଷମବାହୁ ତ୍ରିଭୁଜ ।

(v) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(-2, 3), B(8, 3) ଓ C(6, 7) ।

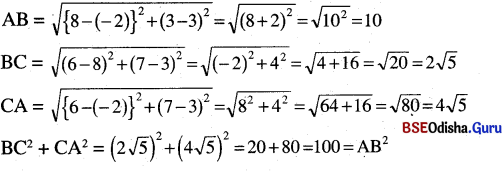
∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।

(vi) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(-2, 3), B(8, 3) ଓ C(6, 7) ।

∴ ABC ଏକ ସମକୋଣୀ ସମବାହୁ ତ୍ରିଭୁଜ ।

Question 6.
ଦର୍ଶାଅ ଯେ ନିମ୍ନଲିଖ୍ ବିନ୍ଦୁଗୁଡ଼ିକ ପାର୍ଶ୍ଵରେ ସୂଚିତ ଚିତ୍ରକୁ ଗଠନ କରିବ ।
(i) (-8, 3), (-2, -1), (6, -2) ଓ (0, 2) (ସାମାନ୍ତରିକ ଚିତ୍ର)
(ii) (-2, -1), (1, 0), (4, 3) ଓ (1, 2) (ସାମାନ୍ତରିକ ଚିତ୍ର)
(iii) (0, -1), (2, 1), (0, 3) ଓ (-2, 1) (ବର୍ଗ ଚିତ୍ର)
(iv) (0,5), (-1, 2), (-4, 3) ଓ (-3, 6) (ବର୍ଗ ଚିତ୍ର)
(v) (-2, 3), (-4, -1), (-6, 0) ଓ (-4, 4) (ଆୟତ ଚିତ୍ର)
ସମାଧାନ :
(i) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(-8, 3), B (-2, -1), C (6,-2) ଓ D(0, 2)

∴ ABCD ଚତୁର୍ଭୁଜର AB = CD ଏବଂ AD = BC ।
⇒ ଚତୁର୍ଭୁଜଟି ସାମାନ୍ତରିକ ଚିତ୍ର ଅଟେ । (ପ୍ରମାଣିତ)
(ABCD ଚତୁର୍ଭୁଜର ବିପରୀତ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ)

(ii) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(-2, -1), B(1, 0), C(4, 3) ଓ D(1, 2)

∴ ABCD ଚତୁର୍ଭୁଜର AB = CD ଏବଂ AD = BC ।
⇒ ଚତୁର୍ଭୁଜଟି ସାମାନ୍ତରିକ ଚିତ୍ର ଅଟେ । (ପ୍ରମାଣିତ)
(ABCD ଚତୁର୍ଭୁଜର ବିପରୀତ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ)

(iii) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(-2, -1), B(1, 0), C(4, 3) ଓ D(1, 2)

(iv) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(0,5), B(-1, 2), C(-4, 3) ଓ D(-3, 6)

(v) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(-2, 3), B(-4, -1), C(-6, 0) ଓ D(-4, 4)

Question 7.
ଦର୍ଶାଅ ଯେ P (1, 1) ବିନ୍ଦୁ A (0, 2), B (2, 0) ଓ C (0, 0) ବିନ୍ଦୁମାନଙ୍କଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।
ସମାଧାନ :
AP = \(\sqrt{(0-1)^2 +(2-1)^2}\) = \(\sqrt{1^2 + 1^2}\) = √2
BP = \(\sqrt{(2-1)^2+(0-1)^2}\) = \(\sqrt{1^2+(-1)^2}\) = √2
CP = \(\sqrt{(0-1)^2+(0-1)^2}\) = \(\sqrt{(-1)^2 +(-1)^2}\) = √2
∴ AP = BP = CP ତେଣୁ ‘P’ ବିନ୍ଦୁ A, B ଓ C ବିନ୍ଦୁମାନଙ୍କଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

Question 8.
xର କେଉଁ ମାନ ପାଇଁ C (x, 3) ବିନ୍ଦୁ, A (2, 4) ଓ B (3, 5) ବିନ୍ଦୁଦ୍ଵୟ ଠାରୁ ସମାନ ଦୂରରେ ରହିବ ?
ସମାଧାନ :
C (x, 3), ବିନ୍ଦୁ A (2, 4), B (3, 5) ବିନ୍ଦୁଦ୍ଵୟଠାରୁ ସମଦୂରରେ ହେବେ।
AC² = (2 – x)² + (4 – 3)² = (2 – x)² + 1
BC² = (3 – x)² + (5 – 3)² = (3 – x)² + 4
କିନ୍ତୁ ଦଉ ଅନ୍ଥି AC = BC ⇒ AC2 = BC2
⇒ (2 – x)² + 1 = (3 – x)² + 4
⇒ 4 – 4x + x² + 1 = 9 – 6x + x² + 4
⇒ x² – x² + 6x – 4x = 9+ 4 – 5
⇒ 2x = 8 ⇒ x = \(\frac{8}{2}\) = 4
∴ xର ମାନ 4 ପାଇଁ C ବିନ୍ଦୁ A ଓ B ଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ହେବେ ।

Question 9.
P(2, y) ବିନ୍ଦୁ Q (-1, 2) ବିନ୍ଦୁଠାରୁ 5 ଏକକ ଦୂରରେ ରହିଲେ, ଦୁର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
P ଓ Q ବିନ୍ଦୁ ପରସ୍ପରଠାରୁ 5 ଏକକ ଦୂରରେ ଅବସ୍ଥିତ ।
P (2, y) Q) (-1, 2) ମଧ୍ୟରେ ଦୂରତା = \(\sqrt{(1-2)^2+(2-y)^2}\)
ପ୍ରଶ୍ମାନୁସାରେ \(\sqrt{(1-2)^2+(2-y)^2}\) = 5
ଉଭୟ ପାର୍ଶ୍ଵର ବର୍ଗ ନେଲେ, (- 1 – 2)² + (2 – y)² = 5²
⇒ (-3)² + 4 – 4y + y² = 25 ⇒ 9 + 4 + y² – 4y – 25 = 0
⇒ y² – 4y + 12 = 0 ⇒ y² – 6y + 2y + 12 = 0
⇒ y (y – 6) + 2 (y – 6) = 0 ⇒ (y – 6) (y + 2) = 0
⇒ y – 6 = 0 ବା y + 2 = 0 ⇒ y = 6 = 0 ବା y = -2
∴ yର ମାନ 6 କିମ୍ବା – 2 ହେଲେ, PQ = 5 ଏକକ ହେବ ।

Question 10.
ଦର୍ଶାଅ A (1, 1),B (2, 2) & C (3, 3) ଯେ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ରହିବେ ।
ସମାଧାନ :
AB = \(\sqrt{(2-1)^2 +(2-1)^2}\) = \(\sqrt{1^2 +1^2}\) = \(\sqrt{1+1}\) = √2
BC = \(\sqrt{(3-2)^2 +(3-2)^2}\) = \(\sqrt{1^2 +1^2}\) = \(\sqrt{1+1}\) = √2
AC = \(\sqrt{(3-1)^2+(3-1)^2}\) = \(\sqrt{2^2 +2^2}\) = \(\sqrt{4+4}\) = √8 = 2√2
AB + BC = √2 + √2 = 2√2 = AC
⇒ A, B, C ବିଦୁ୍ୟତ୍ରୟ ଏକ ସରଳରେଖାରେ ରହିବେ ।

Question 11.
ଦର୍ଶାଅ A (1, 4), B (-1, 6), C (2, 3) ଯେ ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ।
ସମାଧାନ :
AB = \(\sqrt{(-1-1)^2 +(6-4)^2}\) = \(\sqrt{(-2)^2 +(2)^2}\) = \(\sqrt{4+4}\) = √8 = 2√2
AC = \(\sqrt{(2-1)^2+(3-4)^2}\) = \(\sqrt{1^2 +1^2}\) = √2
BC = \(\sqrt{{2-(-1)}^2 +(3-6)^2}\) = \(\sqrt{(2+1)^2 +(-3)^2}\) = \(\sqrt{9+9}\) = √18 = 3√2
AB + AC = 2√2 + √2 = 3√2 = BC
⇒ B, A, C ଏକ ରେଖ୍ୟ ।

Question 12.
ପ୍ରମାଣ କର ଯେ, (1, 0), (2, -3) ଏବଂ (- 1, 6) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ଓ (1, 0) ବିନ୍ଦୁଟି ଅନ୍ୟ ଦୁଇ ବିନ୍ଦୁର ମଧ୍ୟବର୍ତ୍ତୀ ଅଟେ ।
ସମାଧାନ :
ମନେକର ବିଦୁ୍ୟତ୍ରୟ A (1, 0), B(2, -3) 3 C(-1, 6) ।
AB = \(\sqrt{(2-1)^2+(-3-0)^2}\) = \(\sqrt{1^2 +(-3)^2}\) = \(\sqrt{1+9}\) = √10
BC = \(\sqrt{(-1-2)^2+(6+3)^2}\) = \(\sqrt{(-3)^2+9^2}\) = \(\sqrt{9+81}\) = √90 = 3√10
AC = \(\sqrt{(-1-1)^2 + (6-0)^2}\) = \(\sqrt{(-2)^2 +6^2}\) = \(\sqrt{4+36}\) =√40 = 2√10
AB + AC = √10 + 2√10 = 3√10 = BC
∴ AB + AC = BC ⇒ B-A-C
⇒ A (1, 0), B (2, -3) 3 C (1, -6) ବିଦୁ୍ୟତ୍ରୟଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ହେବେ ।

Question 13.
x ଅକ୍ଷ ଉପରେ ଏକ ବିନ୍ଦୁର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର ଯାହା (5, 4) ଓ (-2, 3) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ହେବ ।
ସମାଧାନ :
ମନେକର x ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ବିନ୍ଦୁଟି A (x,0) ।
ଦିଉ ବିଦୁ୍ଦ୍ଵୟ B (5, 4) ଓ C (- 2, 3) ।
AB² = (5 – x)² + (4 – 0)² = (5 – x)² + 16
AC² = (-2 – x)² + (3 – 0)² = (2 + x)² + 9
ପ୍ରଶ୍ମାବସାକ (2 + x)² + 9 = (5 – x)² + 16 ⇒ 4 + 4x + x² + 9 = 25 – 10x + x² + 16
= 4x + x² + 13 = 41 – 10x + x²
⇒ 14x = 28 ⇒ x =2
= 4x + 10x + x² – x = 41 – 13
∴ x ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ବିନ୍ଦୁଟିର ସ୍ଥାନାଙ୍କ (2, 0) ।

Question 14.
ଯଦି O (0, 0), A (1, 2), B (3, 8) ଏବଂ C (3, – 1) ହୁଏ, ତେବେ ଦର୍ଶାଅ ଯେ, AB = 2CO ।
ସମାଧାନ :
ଦର ବିନ୍ଦୁ ଚାରୋଟି O(0, 0), A(1, 2), B (3, 8) ଏବଂ C (3, – 1) ।
AB = \(\sqrt{(3-1)^2+(8-2)^2}\) = \(\sqrt{2^2+6^2}\) = \(\sqrt{4+36}\) = √40 = 2√10
CO = \(\sqrt{3^2 +(-1)^2}\) = \(\sqrt{9+1}\) = √10
∴ AB = 2√10 = 2CO ⇒ AB = 2CO ।

Question 15.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ଦୁଇ ଶୀର୍ଷବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 3) ବିନ୍ଦୁ (4, 3) ହେଲେ, ତୃତୀୟ ଶୀର୍ଷବିନ୍ଦୁର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର ।
ସମାଧାନ :
ନିମ୍ନସ୍ଥ ଚିତ୍ରରେ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
ଏହାର ଶୀର୍ଷବିନ୍ଦୁ B (0, 3) ଏବଂ C (4, 3) । BC ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁ ।
BC = \(\sqrt{(4-0)^2 +(3-3)^2}\) = \(\sqrt{16+0}\) = √16 = 4 ଏକକ।
ଶୀର୍ଷବିନ୍ଦୁ Aରୁ BC ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ AD x ଅକ୍ଷକୁ P ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
∴ D ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{4+0}{2}\), \(\frac{3+3}{2}\)) = (2,3)