BSE Odisha 10th Class Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(b)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(b)

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) sin (A – B) = sin A – cos A |
(ii) cos (θ + α) + cos (α – θ) = ……….. |
(iii) cos (60° – A) + ………. = cos A |
(iv) sin (30° + A) + sin (30° – A) = ……..|
(v) 2 sin A. sin B = ………… cos (A + B) |
(vi) tan (45° + θ). tan (45° – θ) = …………. |
Solution:

Question 2.

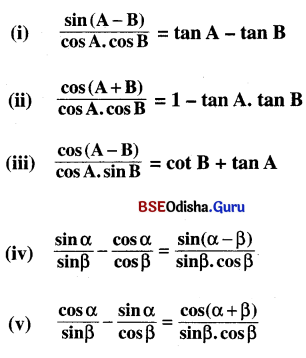
Solution:

Question 3.
ତ୍ପମାଣ କର:
(i) cos (A + 45°) = \(\frac{1}{\sqrt{2}}\) (cos A – sin A)
(ii) sin (45° – θ) = \(\frac{1}{\sqrt{2}}\) (sin θ – cos θ)
(iii) tan (45° + θ) = \(\frac{1+\tan \theta}{1-\tan \theta}\)
(iv) cot (45° + θ) = \(\frac{1+\tan \theta}{1-\tan \theta}\)
Solution:
(i) L.H.S. = cos (A + 45°) = cos A. cos 45° – sin A. sin 45°
= cos A . \(\frac{1}{\sqrt{2}}\) – sin A .\(\frac{1}{\sqrt{2}}\)

(ii) L.H.S. = sin (45° + θ) = sin 45° × cos θ – cos 45° 45° × sin θ
= \(\frac{1}{\sqrt{2}}\) cos θ – \(\frac{1}{\sqrt{2}}\) sin θ = – \(\frac{1}{\sqrt{2}}\) (sin θ – cos θ) = R.H.S.

(iii) L.H.S. = tan (45° + θ) = \(\frac{\tan 45^{\circ}+\tan \theta}{1-\tan 45^{\circ} \cdot \tan \theta}\) = \(\frac{1+\tan \theta}{1-1 \times \tan \theta}\)
= \(\frac{1+\tan \theta}{1-\tan \theta}\) = R.H.S.

(iv) L.H.S. = cot (45° – θ) = \(\frac{\cot 45^{\circ} \cdot \cot \theta+1}{\cot \theta-\cot 45^{\circ}}\) = \(\frac{1 \times \cot \theta+1}{\cot \theta-1}\) = \(\frac{\cot \theta+1}{\cot \theta-1}\)

Question 4.
ତ୍ପମାଣ କର:
(i) cos (45° – A). cos (45° – B) – sin (45° – A). sin (45° – B) = sin (A + B)
(ii) sin (45° + A). cos (20° – A) + cos (45° + A). sin (20° – A) = \(\frac{\sqrt{3}}{2}\)
(iii) cos (65° + θ). cos (35° + θ) + sin (65° + θ). sin (35° + θ) = \(\frac{\sqrt{3}}{2}\)
(iv) cos nθ . cos θ + sin nθ. sin θ = sin (n – 1) θ
(v) tan (60° – A) = \(\frac{\sqrt{3} \cos A-\sin A}{\cos A+\sqrt{3} \sin A}\)
Solution:
(i) L.H.S. = cos (45° – A). cos (45° – B) – sin (45° – A). sin (45° – B)
= cos (45° – A + 45° – B) = cos {90° – (A + B)}
= sin (A + B) = R.H.S.

(ii) L.H.S. = sin (40° + A). cos (20° – A) + cos (40° + A). sin (20° – A)
= sin (40° – A + 20° – A) = sin 60° = \(\frac{\sqrt{3}}{2}\) = R.H.S.

(iii) L.H.S. = cos (65° + θ). cos (35° + θ) + sin (65° + θ). sin (35° + θ)
= cos {(65° + θ) – (35° + θ)} = cos (65° + θ – 35° – θ)
= cos 30° = \(\frac{\sqrt{3}}{2}\) = R.H.S.

(iv) L.H.S. = cos nθ. cos θ + sin nθ. sin θ = cos (nθ – θ)
= sin (n – 1)θ = R.H.S.

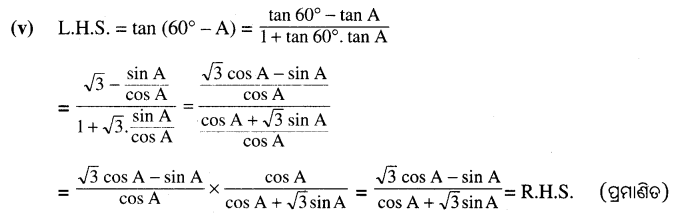
Question 5.
ତ୍ପମାଣ କର:
(i) tan 62° = \(\frac{\cos 17^{\circ}+\sin 17^{\circ}}{\cos 17^{\circ}-\sin 17^{\circ}}\)
(ii) tan 70° = \(\frac{\cos 25^{\circ}+\sin 25^{\circ}}{\cos 25^{\circ}-\sin 25^{\circ}}\)
(iii) tan 7A. tan 4A. tan 3A = tan 7A – tan 4A – tan 3A
(iv) tan (x + y) – tan x – tan y = tan (x + y) . tan x . tan y
(v) (1 + tan 15°) (1 + tan 30°) = 2
(vi) (cot 10° – 1) (cot 35° – 1) = 2
(vii) \(\frac{1}{\cot A+\tan B}\) – \(\frac{1}{\tan A+\cot B}\) = tan (A – B)
(viii) √3 + cot 50° + tan 80° = √3 cot 50° . tan 80°
Solution:

Question 6.
cos 75° ଓ sin 15° ର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
cos 75° = cos (45° + 30°) = cos 45° . cos 30° – sin 45° . sin 30°
= \(\frac{1}{\sqrt{2}}\) . \(\frac{\sqrt{3}}{2}\) – \(\frac{1}{\sqrt{2}}\) × \(\frac { 1 }{ 2 }\) = \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
sin 15° = sin (60° – 45°) = sin 60° . cos 45° – cos 60° . sin 45°
= \(\frac{\sqrt{3}}{2}\) . \(\frac{1}{\sqrt{2}}\) – \(\frac { 1 }{ 2 }\) × \(\frac{1}{\sqrt{2}}\) = \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

Question 7.
(i) cos α = \(\frac { 8 }{ 17 }\) ଓ sin β = \(\frac { 5 }{ 13 }\) ହେଲେ sin (α – β) ର ମାନ ନିଣ୍ଡଯ କର |
(ii) tan A = \(\frac { 1 }{ 2 }\), cot B = 3 ହେଲେ A + B ର ମାନ ନିଣ୍ଡଯ କର |
(iii) tan β = \(\frac{1-\tan \alpha}{1+\tan \alpha}\) ହେଲେ (α + β) ର ମାନ ନିଣ୍ଡଯ କର |
Solution:

Question 8.
A + B + C = 90° ହେଲେ ତ୍ପମାଣ କର ଯେ
(i) cot A + cot B + cot C = cot A . cot B . cot C
(ii) tan A . tan B + tan B . tan C + tan C . tan A = 1
Solution:
(i) A + B + C = 90° ⇒ A + B = 90° – C
⇒ cot (A + B) = cot (90° – C)
⇒ \(\frac{\cot A \cdot \cot B-1}{\cot B+\cot A}\) = tan C = \(\frac{1}{\cot \mathrm{C}}\)
⇒ cot C (cot A. cot B – 1) = 1 (cot B + cot A)
⇒ cot A. cot B. cot C – cot C = cot B + cot A
⇒ cot A. cot B. cot C = cot A + cot B + cot C

(ii) A + B + C = 90° ⇒ B + C = (90° – A)
⇒ tan (B + C) = tan (90° – A)
\(\frac{\tan B+\tan C}{1-\tan B \cdot \tan C}\) = cot A = \(\frac{1}{\tan \mathrm{A}}\)
⇒ tan A (tan B + tan C) = 1 – tan B. tan C
⇒ tan A. tan B + tan C. tan A = 1 – tan B. tan C
⇒ tan A. tan B + tan B. tan C + tan C. tan A = 1

Question 9.
(i) A + B + C = 180° ଏବଂ sin C = 1 ହେଲେ ପ୍ରମାଣ କର ଯେ tan A . tan B = 1
(ii) A + B + C = 180° ହେଲେ ପ୍ରମାଣ କର ଯେ cot A . cot B + cot B . cot C + cot C . cot A = 1
(iii) A + B + C = 180° ଏବଂ cos A = cot B . cos C ହେଲେ ପ୍ରମାଣ କର ଯେ
(a) tan A – tan B + tan C
(b) tan B . tan C = 2
Solution:
(i) sin C = 1 ⇒ sin C = sin 90° ⇒ C = 90°
A + B + C = 180° ⇒ A + B = 180° – C = 180° = 90° = 90°
⇒ A = 90° – B
∴ tan A . tan B = tan (90° – B) . tan B = cot B × tan B = 1

(ii) A + B + C = 180° ⇒ A + B = 180° – C
⇒ cot(A + B) = cot (180° – C)
⇒ \(\frac{\cot A \cdot \cot B-1}{\cot B+\cot A}\) = – cot C
⇒ cot A. cot B – 1=-cot C (cot B + cot A)
⇒cot A. cot B – 1=-cot B. cot C – cot C. cot A
⇒ cot A. cot B + cot B. cot C + cot C. cot A = 1

(iii) (a) A + B + C = 180° ⇒ (A + C) = 180° – A
⇒ sin (B + C) = sin (180° – A)
⇒ sin B . cos C + cos B . sin C = sin A
⇒ \(\frac { sin B. cos C }{ cos A }\) + \(\frac { cos B. sin C }{ cos A }\) = \(\frac { sin A }{ cos A }\) (ଭଉଯ ପାଣରେ cos A କାମାଗଣ)
⇒ \(\frac { sin B. cos C }{ cos B. cos C }\) + \(\frac { cos B. sin C }{ cos B. cos C }\) = tan A
⇒ tan B + tan C = tan A

(b) A + B + C = 180°
⇒ B + C = 180° – A
⇒ cos (B + C) = cos (180° – A) = – cos A
⇒ cos B. cos C – sin B. sin C = – cos B. cos C
⇒ 2cos B. cos C = sin B. sin C
⇒ 2 = \(\frac{\sin B \cdot \cos C}{\cos B \cdot \cos C}\) = tan B. tan C

Question 10.
ଜଣାଥ ଯେ : (i) sin (A + B) . sin (A – B) = sin² A – sin² B
(ii) cos (A + B) . cos (A – B) = cos² A – sin² B
Solution:
(i) L.H.S.= sin (A + B) . sin (A – B)
= (sin A. cos B + cos A· sin B) (sin A · cos B – cos A. sin B)
= (sin A. cos B)² – (cos A. sin B)²
= sin²A. cos²B – cos²A. sin²B
= sin²A (1 – sin²B) − (1 − sin²A) sin²B
= sin²A – sin²A. sin²B – sin²B + sin²A. sin²B
= sin²A – sin²B = R.H.S.

(ii) L.H.S.= cos (A + B) . cos (A – B)
= (cos A. cos B – sin A. sin B) (cos A. cos B + sin A. sin B)
= (cos A. cosB)² – (sin A. sin B)²
= cos²A cos²B – sin²A. sin²B
= cos²A (1 − sin²B) − (1 − cos²A) sin²B
= cos²A – cos²A. sin²B – sin²B + cos²A. sin²B
= cos²A – sin²B = R.H.S.

Question 11.
ପ୍ରମାଣ କର :
(i) sin 50° + sin 40° = √2 sin 85°
(ii) cos 50° + cos 40° = √2 cos 5°
(iii) sin 50° – sin 70° + sin 10° = 0
Solution:
(i) ଦାନପାଣ = sin 50° + sin 40°
= sin (45° +5°) + sin (45° – 5°)
= sin 45°. cos 5° + cos 45°. sin 5° + sin 45°. cos 5° – cos 45°. sin 5°
= 2 sin 45° × cos 5° = 2 × \(\frac{1}{\sqrt{2}}\) cos (90° – 85°)
= √2 sin 85° = ଦର୍ପଣପାଣ

(ii) ଦାନପାଣ = cos 50° + cos 40°
= cos (45° +5°) + cos (45° – 5°)
= cos 45°. cos 5° – sin 45°. sin 5° + cos 45°. cos 5° + sin 45°. sin 5°
= 2 cos 45°. cos 5°
= 2 × \(\frac{1}{\sqrt{2}}\) cos 5° = √2 cos 5° = ଦର୍ପଣପାଣ

(iii) ଦାନପାଣ = sin 50° – sin 70° + sin 10°
= sin (60° – 10°) – sin (60° – 10°) + sin 10°
= (sin 60° . cos 10° – cos 60° . sin 10°)
– (sin 60° . cos 10° + cos 60° . sin 10°) + sin 10°

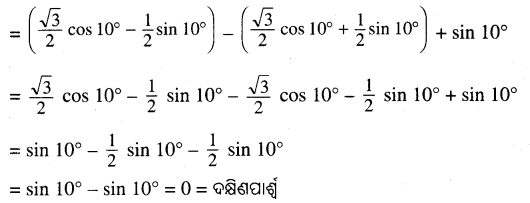
Question 12.
ପ୍ରମାଣ କର :
(i) sin (A + B) = \(\frac{1}{\sqrt{2}}\) , cos (A – B) = \(\frac{1}{\sqrt{2}}\)
(ii) cos (A + B) = – \(\frac { 1 }{ 2 }\) , sin (A – B) = \(\frac { 1 }{ 2 }\)
(iii) tan (A – B) = \(\frac{1}{\sqrt{2}}\) = cot (A + B)
(iv) tan (A + B) = -1, cosec (A – B) = √2
Solution:
(i) sin (A + B) = \(\frac{1}{\sqrt{2}}\) = sin 45°ଦା, sin 135°
⇒ A + B = 45° ଦା, 135°
cos (A – B) = \(\frac{1}{\sqrt{2}}\) = cos 45° ⇒ A – B = 45°
A + B = 45° , A – B = 45°
ହେଲେ, (i) ଓ (ii) ରୁ A + B +A – B = 45° + 45° ⇒ 2A = 90° ⇒ A = 45°
B = 45° – 45° = 0°
ଯଦି A + B = 135°, A – B = 45°
∴ (i) ଓ (ii) ରୁ A + B + A – B = 135° + 45°
⇒ 2A = 180° ⇒ A = 90°
B = 135° – 90° = 45°
(∴ A = 45°, B = 0°) ଦା, (A = 90° , B = 45°)

(ii) cos (A + B) = – \(\frac { 1 }{ 2 }\) = cos 120°
⇒ A + B = 120°
sin (A – B) = \(\frac { 1 }{ 2 }\) = sin 30°
⇒ A – B = 30°
∴ (i) ଓ (ii) ରୁ A + B + A – B = 120° + 30°
⇒ 2A = 150° ⇒ A = 75°
B = 120° – 75° = 45° (∵ A = 75°, B = 45°)

(iii) tan (A – B) = \(\frac{1}{\sqrt{3}}\) = tan 30° ⇒ A – B = 30°
cot (A + B) = \(\frac{1}{\sqrt{3}}\) = cot 60° ⇒ A – B = 30°
∴ (i) ଓ (ii) ରୁ A + B + A – B = 60° + 30°
⇒ 2A = 90° ⇒ A = 45° , B = 60° – 45° = 15°
∴ A = 45° , B = 15°

(iv) tan (A + B) = -1 = tan 135° ⇒ A + B = 135°
cosec (A – B) = √2 = cosec 45° ⇒ A – B = 45°
(i) ଓ (ii) ରୁ 2A = 180° ⇒ A = 90°
∴ B = 135° – 90° = 45°
∴ A = 90° , B = 45°