BSE Odisha 10th Class Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(c)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(c)

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଗୋଟିଏ ତ୍ରିଭୁଜର ଶୀର୍ଷବିଦୁ୍ୟତ୍ରୟ (2, 5), (-3, 5) ଓ (0, 5) ହେଲେ, ତ୍ରିଭୁଜଟିର କ୍ଷେତ୍ରଫଳ _____ ହେବ ।
[-5, 3, 0, 10]
(ii) ଯଦି a = _____ ହୁଏ, ତେବେ (a, -2), (2, 5) ଓ (2, 10) ବିନ୍ଦୁଦ୍ଵୟ ଏକ ସରଳରେଖାରେ ରହିବେ ।
[0, 3, 2, -2]
(iii) yର ମାନ _____ ପାଇଁ (-2, -2), (0, y) ଓ (3, 3) ବିନ୍ଦୁଦ୍ଵୟ ଏକ ସରଳରେଖାରେ ରହିବେ ।
[0, 2, 2, 3]
(iv) kର ମାନ _____ ପାଇଁ (k, -2), (1, 4) ଏବଂ (-2, 7) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ହେବେ ।
[3, -3, 2, -2]
(v) ଥର ମାନ _____ ପାଇଁ (4, -5), (1, a) ଏବଂ (-2, 7) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିଦୁ୍ୟତ୍ରୟ ଗୋଟିଏ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ ହେବେ ନାହିଁ ।
[1, 2, 3, 4]
ଉତ୍ତର:
(i) 0
(ii) 2
(iii) 0
(iv) 3
(v) 1

Question 2.
ନିମ୍ନରେ କେତେକ ତ୍ରଭୁଜର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟର ସ୍ଥାନଙ୍କ ଦିଆଯାଇଛି । ପ୍ରତ୍ୟେକ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
(i) (3, 0), (4, 5) ଓ (2, 0)
(ii) (0, 0), (1, 0) ଓ (1, 1)
(iii) (-2, 1), (2, -3) ଓ (4, – 4)
(iv) (5,7),(6, 4) ଓ (2, -5)
(v) (5, 2), (1, 3) ଓ (1,-2)
ସମାଧାନ :
(i) ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟର ତ୍ରୟ (3, 0), (4, 5), (2, 0) 1.
ଏଠାରେ x₁ = 3, x₂ = 4, x₃ = 2, y₁ = 0, y₂ = 5, y₃ = 0
∆ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\)|{3(5 – 0) + 4(0 – 0) + 2(0 – 5)}| = \(\frac{1}{2}\)|{15 + 0 – 10}|
= \(\frac{1}{2}\) × 5 = \(\frac{5}{2}\)
∴ ∆ର କ୍ଷେତ୍ରଫଳ \(\frac{5}{2}\) ବର୍ଗ ଏକକ ।

(ii) ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟର ତ୍ରୟ (0, 0), (1, 0), (1, 1) |
ଏଠାରେ x₁ = 1, x₂ = 1, y₁ = 0, y₂ = 1
∴ ∆ ର ଏକ ଶୀର୍ଷବିନ୍ଦୁ ମୂଳବିନ୍ଦୁ ହୋଇଥିବାରୁ ଏହାର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|(x₁y₂ – x₂y₁)|
= \(\frac{1}{2}\)|(1 × 1 – 0 × 1)| = \(\frac{1}{2}\)|(1 – 0)| = \(\frac{1}{2}\) × 1 = \(\frac{1}{2}\) ବର୍ଗ ଏକକ ।

ବିକତ୍ଵ ସମାଧାନ :
ଏଠାରେ x₁ = 0, x₂ = 1, x₃ = 1, y₁ = 0, y₂ = 0, y₃ = 1
∴ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\)|{0(0 – 1) + 1(1 – 0) + 1(0 – 0)}| = \(\frac{1}{2}\)(0 + 1 + 0) = \(\frac{1}{2}\)

(iii) ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟର ତ୍ରୟ (-2, 1), (2, -3), (4, -4) ।
ଏଠାରେ x₁ = -2, x₂ = 2, x₃ = 4, y₁ = 1, y₂ = -3, y₃ = -4
∴ ∆ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\)|{-2(-3 + 4) + 2(-4 – 1) + 4(1 + 3)}|
= \(\frac{1}{2}\)|(-2) + (-10) + 16| = \(\frac{1}{2}\) × 4 = 2 ବର୍ଗ ଏକକ ।

(iv) ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟର (5,7), (6, 4), (2,-5) ।
ଏଠାରେ x₁ = -5, x₂ = 6, x₃ = 2, y₁ = 7, y₂ = 4, y₃ = -5
∴ ∆ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\)|{5(4 + 5) + 6(-5 – 7) + 2(7 – 4)}|
= \(\frac{1}{2}\)(45 – 76 + 6) = \(\frac{1}{2}\)|(51 – 72)| = \(\frac{1}{2}\)|-21|
= \(\frac{21}{2}\) = 10.5 ବର୍ଗ ଏକକ ।

(v) ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟର (5, 2), (1, 3) ଓ (1,-2) ।
ଏଠାରେ x₁ = 5, x₂ = -1, x₃ = 1, y₁ = 2, y₂ = 3, y₃ = -2
∴ ∆ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\)|{5 (3 + 2) + (-1) (-2 – 2) + 1(2 – 3)}|
= \(\frac{1}{2}\)|{25 + 4 – 1}| = \(\frac{1}{2}\) × 28 = 14 ବର୍ଗ ଏକକ ।

Question 3.
ଦର୍ଶାଅ ଯେ, ଦତ୍ତ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ।
(i) (1, 1), (4, 3) ଓ (-2, -1)
(ii) (-1,-5), (0, -3) ଓ (4, 5)
(iii) (1,4), (3, -2) ଓ (-3, 16)
(iv) (-4a, – 6a), (-a, -2a) ଓ (5a, 6a)
(v) (-a, 2b), (0, b) ଓ (\(\frac{a}{2}, \frac{b}{2}\))
ସମାଧାନ :
(i) ବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନୀଙ୍କ A (1, 1), B (4, 3) ଓ C (-2, -1) ।
ଏଠାରେ x₁ = 1, x₂ = 4, x₃ = -2, y₁ = 1, y₂ = 3, y₃ = -1
ABC ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) | { 1 (3 + 1) + 4 (-1 – 1 ) + ( -2) (1 – 3)}| = \(\frac{1}{2}\) |4 – 8 + 4| = \(\frac{1}{2}\) (0) = 0
∴ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ।

(ii) ବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନୀଙ୍କ (-1, -5), B (0, -3) ଓ C (4, 5) ।
ଏଠାରେ x₁ = -1, x₂ = 0, x₃ = 4, y₁ = -5, y₂ = -3, y₃ = 5
ABC ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) | { (-1) (-3 – 5) + 0 (5 + 5) + 4 (-5 + 3)}|
= \(\frac{1}{2}\) |(-1)(-8) + 0 + 4(-2)| = \(\frac{1}{2}\) (8 – 8) = \(\frac{1}{2}\) (0) = 0
∴ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ।

(iii) ବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନୀଙ୍କ A(1, 4), B (3, -2) ଓ C (-3, 16) ।
ଏଠାରେ x₁ = 1, x₂ = 3, x₃ = -3, y₁ = 4, y₂ = -2, y₃ = 16
ABC ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) |{ 1 (-2 – 16) + 3 (16 – 4) + (- 3) (4 + 2)}|
= \(\frac{1}{2}\) |(- 18 + 36 – 18)| = \(\frac{1}{2}\) (0) = 0
∴ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ।

(iv) ବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନୀଙ୍କ A(-4a, -6a), B (-a, -2a) ଓ C (5a, 6a) ।
ଏଠାରେ x₁ = -4a, x₂ = -a, x₃ = 5a, y₁ = – 6a, y₂ = – 2a, y₃ = 6a
ABC ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ
= \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) |{(- 4a) (-2a – 6a) + (- a) (6a + 6a) + 5a (- 6a + 2a)}|
= \(\frac{1}{2}\) | (32a² – 12a² – 20a²) | = \(\frac{1}{2}\) (0) = 0
∴ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ।

(v) ବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନୀଙ୍କ A (-a, 2b), B (0, b) ଓ C(\(\frac{a}{2}, \frac{b}{2}\))
ଏଠାରେ x₁ = -a, x₂ = 0, x₃ = \(\frac{a}{2}\), y₁ = 2b, y₂ = b, y₃ = \(\frac{b}{2}\)

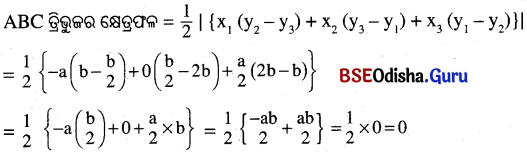
∴ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ।

Question 4.
ଗୋଟିଏ ତ୍ରିଭୁଜର ଶୀର୍ଷନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ (1, -3), (2, -5) ଓ (x, 1) ଏବଂ କ୍ଷେତ୍ରଫଳ 4 ବର୍ଗ ଏକକ ହେଲେ, xର ମାନ ନିରୂପଣ କର ।
ସମାଧାନ :
ଗୋଟିଏ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ A(1, – 3), B(2, -5) ଓ C (x, 1)।
ଏବଂ କ୍ଷେତ୍ରଫଳ 4 ବର୍ଗ ଏକକ ।
ଏଠାରେ x₁ = 1, x₂ = 2, x₃ = x, y₁ = – 3, y₂ = – 5, y₃ = 1
ABC ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) | 1 (-5 – 1) + 2 (1 + 3) + x (- 3 + 5) |
= \(\frac{1}{2}\) | 1 -6 + 8 + 2x | = \(\frac{1}{2}\) | 2x + 21 | = \(\frac{1}{2}\) × 2 (x + 1) = x + 1
ପ୍ରଶ୍ନନୁସାରେ, x + 1=4 ⇒ x = 4 – 1 = 3 ∴ x = 3

Question 5.
k ର କେଉଁ ମୂଲ୍ୟ ପାଇଁ (3, – 5), (k, 0) ଓ (-4, 7) ସ୍ଥାନାଙ୍କ ବିନ୍ଦୁମାନଙ୍କ ଦ୍ୱାରା ଗଠିତ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ \(\frac{95}{2}\)ବର୍ଗ ଏକକ ହେବ ?
ସମାଧାନ :
ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A (3, -5), B (k, 0) ଓ C (-4, 7) ।
ଏଠାରେ x₁ = 3, x₂ = k, x₃ = -4, y₁ = – 5, y₂ = 0, y₃ = 7
ABC ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) |{3 (0 – 7) + k (7 + 5) + (-4) (-5 – 0)}|
= \(\frac{1}{2}\) |{- 21 + 12 k + 20}| = \(\frac{1}{2}\) (12 k – 1)
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1}{2}\) (12 k – 1) = \(\frac{95}{2}\) ⇒ 12k – 1 = 95 ⇒ 12 k = 96 ⇒ k = \(\frac{96}{12}\) = 8
∴ kର ମାନ 8 ହେଲେ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ \(\frac{95}{2}\) ବର୍ଗ ଏକକ ହେବ ।

Question 6.
(2, 3), (0, 5) ଓ (1, y) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ରହିଲେ, Yର ମାନ ନିରୂପଣ କର ।
ସମାଧାନ :
ବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନାଙ୍କ A (2, 3), B (0, 5) & C (1, y) |
ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) | 2 (5 – y) + 0 ( y – 3) + 1 (3 – 5) | = \(\frac{1}{2}\) | 10 – 2y + 0 – 21 = \(\frac{1}{2}\) | -2y + 8 |
= \(\frac{1}{2}\) (2y – 8) = \(\frac{1}{2}\) × 2 (y – 4) = y – 4
ପ୍ରଶ୍ନନୁସାରେ, y – 4 = 0 = y = 4
∴ yର ମୂଲ୍ୟ 4 ହେଲେ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ 0 ହେବ ।
ଅର୍ଥାତ୍ (2, 3), (0, 5) ଓ (1, y) ଏକ ସରଳରେଖାରେ ରହିବେ ।

Question 7.
k ର କେଉଁ ମୂଲ୍ୟ ପାଇଁ (2, 3), (3, k) ଏବଂ (5, 9) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ହେବେ ?
ସମାଧାନ :
ଦଉ ବିନ୍ଦୁତ୍ରୟ A (2, 3), B (3, k) ଏବଂ C (5, 9) ।
ଏଠାରେ x₁ = 2, x₂ = 3, x₃ = 5, y₁ =3, y₂ = k, y₃ = 9
∆ ABC ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)|{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) | {2 (k – 9) + 3(9 – 3) + 5 (3 – k)} |
= \(\frac{1}{2}\) | (2k – 18 + 18 + 15 – 5k) | = \(\frac{1}{2}\) (-3k + 15) | = \(\frac{1}{2}\) (3k – 15)
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1}{2}\) (3k – 15) = 0 ⇒ 3k – 15 = 0 ⇒ k = \(\frac{15}{3}\) = 5
∴ kର ମାନ 5 ପାଇଁ (2, 3), (3, k) ଏବଂ (5, 9) ଏକ ସରଳରେଖାରେ ରହିବେ ।

Question 8.
କେଉଁ ସର୍ଭରେ (1, 1), (3, 5) ଓ (x, y) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ରହିବେ, ସ୍ଥିର କର ।
ସମାଧାନ :
ଦତ୍ତ ବିନ୍ଦୁତ୍ରୟ A (1, 1), B (3, 5) ଓ C (x, y) ।
ଏଠାରେ x₁ = 1, x₂ = 3, x₃ = x, y₁ = 1, y₂ = 5, y₃ = y
ABC ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) |{x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)}|
= \(\frac{1}{2}\) | 1 (5 – y) + 3 ( y – 1 ) + x (1 – 5) | = \(\frac{1}{2}\) | (5 – y + 3y – 3 + x – 5x) |
= \(\frac{1}{2}\) | (2 y – 4x + 2) | = \(\frac{1}{2}\) × 2 (2x – y – 1) = (2x – y – 1)
ପ୍ରଶ୍ନନୁସାରେ, 2x – y – 1=0 ⇒ 2x – y = 1
∴ 2x – y = 1 ହେଲେ (1, 1), (3, 5) ଓ (x, y) ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ରହିବେ ।

Question 9.
ଏକ ଚତୁର୍ଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ (1, 0), (2, 4), (0, 5) ଓ (-2, 1) ହେଲେ, ତାହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏକ ଚତୁର୍ଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ (1, 0), (2, 4), (0, 5) 8 (-2, 1) ।
∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନାଙ୍କ A (1, 0), B (2, 4), C (0, 5) ।
ଏଠାରେ x₁ = 1, x₂ = 2, x₃ = 0, y₁ = 0, y₂ = 4, y₃ = 5

Question 10.
ଏକ ଚତୁର୍ଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ (- 2, 3), (3, -2), (7, 4) ଓ (1, 5) ହେଲେ, ତାହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏକ ଚତୁର୍ଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ A (-2, 3), B (3, -2), C (7, 4) ଓ D (1, 5) ।
AC କଣ୍ଠକୁ ଯୋଗକଲେ ଚତୁର୍ଭୁଜଟି ∆ ABC ଓ ∆ ACD ଦୁଇଟି ତ୍ରିଭୁଜରେ ପରିଣତ ହେବ ।
∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନାଙ୍କ A(-2, 3), B (3, – 2) ଓ C (7, 4) ।
ଏଠାରେ x₁ = -2, x₂ = 3, x₂ = 7, y₁ = 3, y₂ = -2, y₃ = 4

∴ ABCD ଚତୁର୍ଭୁଜଟିର କ୍ଷେତ୍ରଫଳ = ∆ ABCର କ୍ଷେତ୍ରଫଳ + ∆ ACDର କ୍ଷେତ୍ରଫଳ
= 25 ବର୍ଗ ଏକକ + 7.5 ବର୍ଗ ଏକକ = 32.5 ବର୍ଗ ଏକକ ।

Question 11.
∆ ABCରେ A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (1, 1) ଓ AB, AC ବାହୁ ଦ୍ବୟର ମଧ୍ୟବିନ୍ଦୁ ଯଥାକ୍ରମେ D (-1, – 2) ଓ E (3, 2) ହେଲେ B ଓ Cର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କରି ∆ ABCର କ୍ଷେତ୍ରଫଳ ସ୍ଥିର କର ।
ସମାଧାନ :
∆ ABCର A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (1, 1) ।
AB ଓ ACର ମଧ୍ୟବିନ୍ଦୁ ଯଥାକ୍ରମେ D (-1, -2) ଓ E (3, 2) ।
ମନେକର B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x₂, y₂) ଏବଂ C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x₃, y₃) ।

Question 12.
(3, 0), (5, – 1) ଓ (p, p) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ହେଲେ pର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
A (3, 0), B (5, -1), C (p, p) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ।
∆ ABCର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) | 3 (- 1 – p) + 5 (p – 0) + p (0 + 1) | = 0 ହେବ।
⇒ \(\frac{1}{2}\) | – 3 – 3p + 5p + p | ⇒ \(\frac{1}{2}\) | 3p – 3 | = 0
⇒ \(\frac{3p-3}{2}\) = 0 ⇒ 3p = 3 ⇒ p = \(\frac{3}{3}\) =1
∴ pର ମୂଲ୍ୟ 1 ହେଲେ (3, 0), (5, -1), (p, p) ଏକରେଖ୍ୟ ହେବେ ।

Question 13.
(p, 2p), (3p, 3p) ଓ (3, 1) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ହେଲେ pର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
A (p, 2p), B (3p, 3p), C (3, 1) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ।
∆ ABCର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) | p(3p – 1) + 3p (1 – 2p) + 3 (2p – 3p) | = 0 ହେବ ।
⇒ \(\frac{1}{2}\) | 3p² – p + 3p – 6p² – 3p | ⇒ \(\frac{1}{2}\) |- 3p² -p | = 0
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1}{2}\) (3p² + p) = 0 ⇒ p (3p + 1) = 0 ⇒ p =0 ବା p = \(– \frac{1}{3}\)

Question 14.
(x, -1), (2, -1), (2, 1) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ହେଲେ xର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
A (x,-1), B (2, 1), C (2, 1) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ।
A ABCର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) | x(- 1 – 1 ) + 2 (1 + 1) + 2 (- 1 + 1) | = 0 ହେବ ।
= \(\frac{1}{2}\) | -2x + 4 + 0 | = 0 ⇒ \(\frac{1}{2}\) | – (2x – 4)|= 0
⇒ \(\frac{1}{2}\) (2x – 4) = 0 ⇒ x – 2 =0 ∴ xର ମୂଲ୍ୟ 2 ।

Question 15.
(x, y) ବିନ୍ଦୁଟି (a, 0) ଓ (0, b) ବିନ୍ଦୁ ଦୁଇଗୋଟିର ସଂଯୋଗକାରୀ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ହେଲେ ପ୍ରମାଣ କର ଯେ, \(\frac{x}{a}+\frac{y}{b}=1\) ।
ସମାଧାନ :

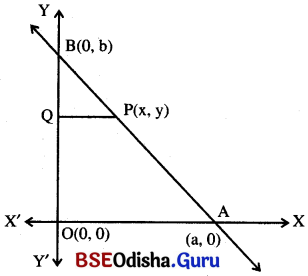
ଦତ୍ତ ଚିତ୍ରରେ O ମୂଳବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 0) ।
A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a, 0), B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, b) ।
ଏଠାରେ OA = a ଏକକ, OB = b ଏକକ
P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
P ବିନ୍ଦୁରୁ y-ଅକ୍ଷ ପ୍ରତି ଲମ୍ବ PQ ।
∴ OQ = y ଏବଂ PQ = x
⇒ BQ = OB – OQ = b – y
∆ BOP ଓ A BOA ମଧ୍ୟରେ m∠BQP = m∠BOA (ସମକୋଣ)
∠A ଉଭୟ ତ୍ରିଭୁଜର ସାଧାରଣ କୋଣ ।
∴ ଅବଶିଷ୍ଟ m∠BPQ = m∠BAO ∴ ∆ BOP ~ ∆ BOA
⇒ \(\frac{PQ}{OA}=\frac{BQ}{OB}\) ⇒ \(\frac{x}{a}=\frac{b-y}{b}\) ⇒ \(\frac{x}{a}=\frac{ b}{b}-\frac{y}{b}\) ⇒ \(\frac{x}{a}+\frac{y}{b}=1\)

Question 16.
ପ୍ରମାଣ କର ଯେ, (a, b), (a, b) ଓ (a – a, b – b) ବିଦୁ୍ ତ୍ରୟ ଏକରେଖୀୟ ନୁହେଁ ।
ସମାଧାନ :
A (a, b), B (a’, b’) ଓ (a – a’, b – b’) ବିଦୁ୍ତ୍ରୟ ଏକ ରେଖୀୟ ହେବେ
ଯଦି A, B ଓ C ଶୀର୍ଷବିନ୍ଦୁ ବିଶିଷ୍ଟ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ () ହେବ ।
∴ ∆ ABCର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) | a (b’ – b + b’) + a’ (b – b’ – b) + (a – a’) (b – b’) |
= \(\frac{1}{2}\) | (ab’ – ab + ab’ – a’b’ + ab – ab’ – a′b + a’b’) |
= \(\frac{1}{2}\) | ab’ + ab’ – ab’ – ab + ab – ab’ + a’b’ – ab ] = \(\frac{1}{2}\) (ab’ – a’b)
∴ ଏଠାରେ ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖୀୟ ନୁହଁନ୍ତି । କାରଣ, ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ନୁହେଁ ।

Question 17.
A (p + 1, 1), B (2p + 1, 3) ଓ C (2p + 2, 2p) ବିନ୍ଦୁ ତ୍ରୟ ଏକ ରେଖୀୟ ହେଲେ pର ମାନ ସ୍ଥିର କର ।
ସମାଧାନ :
A (p + 1, 1), B (2p + 1, 3) ଓ C (2p + 2, 2p) ବିଦୁ୍ତ୍ରୟ ଏକରେଖୀୟ ।
∴ ∆ ABCର କ୍ଷେତ୍ରଫଳ = 0
⇒ \(\frac{1}{2}\) | (p + 1) (3 – 2p) + (2p + 1) (2p – 1) + (2p + 2) (1 – 3) | = 0
⇒ \(\frac{1}{2}\) | 13p + 3 – 2p² – 2p + 4p² – 1 – 4p – 4 | = 0
⇒ \(\frac{1}{2}\) | 2p² – 3p – 2 | = \(\frac{1}{2}\) (2p² – 3p – 2) = 0
⇒ \(\frac{1}{2}\) (2p² – 3p – 2) = 0
⇒ 2p² – 3p – 2 = 0 ⇒ 2p² – 4p + p – 2 = 0
⇒ 2p (p – 2) + 1 (p – 2) = 0 ⇒ (p – 2) (2p + 1) = 0
⇒ p – 2 = 0 କିମ୍ବା 2p + 1 = 0 ⇒ p = 2 କିମ୍ବା P = \(– \frac{1}{2}\)

Question 18.
(x, y), (3, 4) 3 (-5, -6) ବିନ୍ଦୁ ତ୍ରୟ ଏକ ରେଖୀୟ ହେଲେ ପ୍ରମାଣ କର ଯେ 5x – 4y+ 1 = 0 ।
ସମାଧାନ :
A (x, y), B(3, 4) 3 C (-5, -6) ବିଦୁ୍ତ୍ରୟ ଏକରେଖୀୟ ।
∆ ABCର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) | x (4 + 6) + 3 (-6 – y) + (5) (y – 4) | = 0 ହେବ ।
⇒ \(\frac{1}{2}\) | 10 x – 18 – 3y – 5y + 20 | = 0 ⇒ \(\frac{1}{2}\) | 10x – 8y + 2 | = 0
⇒ \(\frac{1}{2}\) (10x – 8y + 2) = 0 ⇒ 5x – 4y + 1 = 0 (ପ୍ରମାଣିତ)